數學歸納法的教學實踐與思考

福建省福安市第二中學 阮云慶

數學歸納法是數學證明中的一種重要方法，其證明過程的兩個步驟缺一不可。通過反復練習與強調也難以把握這一方法的實質，體會其辯證的思想策略和內涵。為什么證題時一定要分兩步進行？為什么證了這兩步之后能對無窮多個自然數結論成立？學生感到困惑、茫然。除了學生的思維和認識上的局限外，另一個重要原因是教師對教材處理不當引起的。以下談談自己的教學實踐與思考。

一、理解數學歸納法原理的內涵

1.數學歸納法兩個步驟的辯證關系

數學歸納法是通過“有限”來解決“無限”的一種遞推證明方法。它的證明有兩個步驟，第一步是遞推的基礎，第二步是遞推的依據，兩者之間的抽象關系是學生認知的障礙。如何將學生原有的經驗轉換成適合于新情況所需要的認知結構，一個簡捷的途徑是：將現有的認知結構融合新知識，把新知識同化于現有認知結構。因此，我將原理想象成一個游戲模型或多米諾骨牌，將一排錄音磁帶按適當距離豎直排列，以磁帶倒下表示命題正確，推倒第一塊（表示n取第一個值n0時，命題正確），要保證所有的磁帶都倒下（n∈N時命題正確）必須滿足什么條件？每一塊倒下（n=k，k∈N,k≥n0時命題正確），都能保證其后面的一塊倒下（n=k+1時命題正確），從而使數學歸納法的本質直觀化。

2.驗證n取第一個值時命題正確的必要性

由于教師強調，學生自然認同數學歸納法的兩個步驟，但對驗證值取第一個值時命題正確的必要性的認識可能還不夠深刻，需要設計如下式子的證明，幫助學生體會初始值驗證的重要性。

證明：2+4+6+…+2n=n2+n+1(n∈N)。

學生：假設當n=k時，等式成立，即2+4+6+…+2k=k2+k+1，則當n=k+1時，2+4+6+…+2k+2(k+1)=k2+k+1+2(k+1)=(k+1)2+(k+1)+1，∴n=k+1時，等式成立。所以對所有的正整數n，都有等式成立。

學生并沒有認識到遞推基礎的重要性，只知數學歸納法的步驟，而沒有領悟到原理和實質。所以在數學歸納法的教學實踐中遇到學生種種的錯誤或困難是很正常的。

二、遞推過程中的證題技巧與方法

數學歸納法應用于五類問題的證明，即恒等式、整除性問題、條件等式、不等式和某些幾何問題的證明，從證題模式看似乎簡單、呆板，其實在遞推過程中體現出的證題技巧、方法和數學思想，對培養學生的邏輯思維能力和解題能力卻不容置疑。其基本思路是：從歸納假設出發，分析P(k)與P(k+1)的差異及聯系，利用折項、添項、放縮、作差、分析等手段，或從P(k+1)中分離出P(k)再進行局部調整，也可以考慮尋求二者的“接口”，以便過渡。其中體現了高超的數學技巧和豐富的數學思想方法以及對學生的能力要求和教師的教學技能的挑戰。

例1 當n∈N,n≥2時，求證：

證明：（1）當n=2時，不等式成立。

（2）設n=k時，不等式成立,即則n=k+1時，（學生往往以為“n=k”到“n=k+1”增加一項），∴n=k+1時，不等式成立。

由（1）（2）可知對于任意n∈N(n≥2)，不等式都成立。

三、錯誤辨析的教學環節

數學歸納法的證題步驟學生較易接受，但對原理的理解要靠方法來揭示和解決，巧妙地設計一些典型的證題錯誤進行辨析，可提高教材實質性內容的深度，引發學生在認識上產生適當的“矛盾”和“沖突”，使他們發覺在理解數學歸納法時還存在下列不當之處。

證明：（1）當n=1時，結論正確。

（2）設n=k時，結論正確，即成立，則n=k+1時，

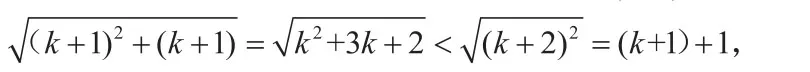
當n=k+1時，結論成立。

所以由（1）（2）可知，對于任意n∈N，都有

上面的解法貌似是數學歸納法，但第二步驟推理沒有運用n=k時的歸納假設，這種推理實質上是沒有根據的，缺失傳遞性。

例3 對任意的自然數n，求證：

證明：（1）當n=1時，不等式顯然成立。

（2）假設n=k時，不等式成立，即則n=k+1時,

∴n=k+1時，不等式成立。

由（1）（2）可知，對任意的自然數n,都有

在第一步驗證n=n0后，數學歸納法要求第二步所考慮的k必須滿足k≥n0,本題第二步成立要求k≥2,因此必須依次驗證n=1和n=2時不等式成立。

證明:（1）當n=1時，a1=1，所以不等式成立。

（2）假設n=k時命題正確，即有成立，則n=k+1時，

∴n=k+1命題正確。

所以由（1）（2）知對于任意n∈N，都有命題正確。

分析：上述證明犯了偷換歸納假設錯誤，假設當n=k時，與 當n=k+1時中的 不同取值，于是不能將作為歸納假設進行遞推。由則應用此不等式結合分析法實施轉化才是正理。

4.猜想與證明

數學命題的論證通常始于不完全歸納，再加以邏輯推理的證明。數學歸納法從論證的方法上綜合了歸納和演繹，這種通過“觀察—歸納—猜想—證明”發現問題和解決問題的方法，是培養學生探索新問題、歸納新方法、培養數學能力和創新思維的金鑰匙。

猜想：an=2n-1,Sn=n2。可用數學歸納法證明此猜想的正確（證明略）。從特殊到一般也符合人類的認知規律，合情推理和演繹推理在這兒相得益彰、各領風騷。

數學教育家弗賴登塔爾認為，學習數學歸納法的正確途徑是向學生提出一些必須用數學歸納法才能解決的問題，迫使他們直觀地去使用這個方法。在學生發現和懂得了這個方法后，再去幫助他們用抽象形式把它敘述出來。數學歸納法的教學不簡單，需要師生的默契配合，需要師生數學素養的提高，需要學生思維能力的有效訓練，數學教學也需要時間，靜待花開。