數形結合思想在三角函數教學中的運用

江蘇省射陽縣高級中學 王翠霞

由于三角函數具有抽象性的特點，學生往往學習起來會感到比較困難，因此，要想讓學生能比較輕松地學習三角函數，讓學生對三角函數的知識點有直觀的認識是關鍵。數形結合可以將抽象的數學問題更加直觀地展示出來，因此通過運用“數形結合”的思想，可以很好地幫助學生學習三角函數。本文將淺談數形結合在三角函數中的應用。

一、利用圖象，記牢函數性質

在整個函數學習中，由于三角函數的函數性質主要有定義域、值域、周期性、單調性和奇偶性，內容較多，學生們對三角函數的一些知識點不能記牢，而三角函數的函數性質是歷年考試的重點。為了克服這些困難，可以利用圖象，運用數形結合的思想，記牢函數性質。

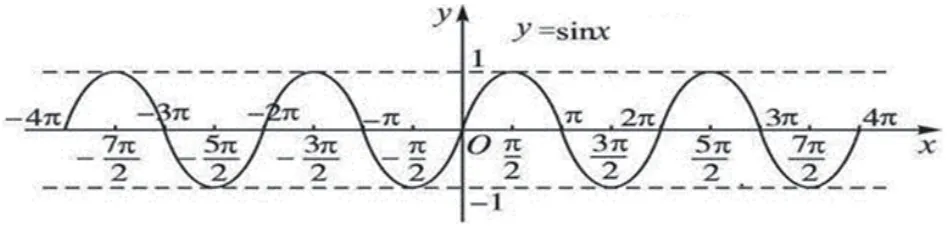
為1，最小值為-1，圖象在[-1,1]之間，因此可以確定其值域為[-1,1]。圖象在上是一樣的，這就可以推斷出其為周期函數，而周期為圖象整體有增有減，是沒有單調性的,但是細看圖象在上是單調遞增的，在上是單調遞減的，因此我們可以從中發現規律，推出其單調增區間為單調減區間為其圖象關于原點對稱，因此可以得出該函數是奇函數。通過函數圖象，我們可以更加生動、直觀地看出并得到其函數性質。

二、利用圖象，確定函數值正負

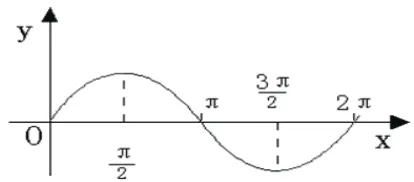
許多三角函數的題目需要確定函數值的正負，而且函數值的正負確定是解決一個題目的基礎。許多同學在做題目的時候經常不能很清楚地確定函數值的正負，其實出現這些問題的原因有二:一是學生在演算時由于粗心大意而出現的失誤，二是學生根本就不知道怎么確定函數值的正負。其實以上兩種原因都可以通過畫出函數圖象來解決。

利用函數圖象，我們只需把自變量的范圍在圖象上標注出來，即可確定函數值的正負，這樣不僅可以避免學生在演算時由于粗心大意而出現失誤，而且能更直觀地向學生們展示如何確定正負號。

三、利用圖象，比較函數值大小

學生在做題時經常會遇到這樣一類題目：給出角度的范圍，比較三角函數值大小。可能有些學生在解答的時候會帶入特殊值，從而比較函數值的大小，其實運用特值的思想是可以的，但是其實這并不是出題者的本意，而且有些題目是無法用特值來解答的。當遇到比較函數值大小的題目時，畫出圖象，利用數形結合的思想，才是出題者的意圖和解答本類題目的關鍵。

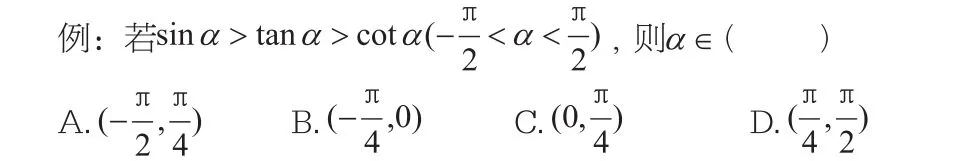
解析：可能許多學生拿到這個題目的時候，就不知道怎么去做了，因為不能用特值了。其實本題目運用到了數形結合的思想，通過畫出單位圓來進行解題。從已知條件：再根據的函數性質，可以得出再根據可以得畫出圖形，可以得出,從而確定是

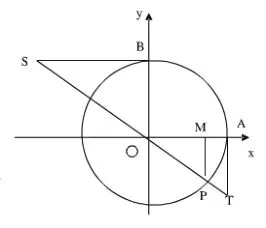
如果單純從數出發，不僅比較抽象，難以讓人理解，而且會容易引起計算的錯誤。通過運用數形結合的思想畫出圖象，可以快速地將題目解答出來，不僅條理清晰，而且可以避免對函數值的正負判斷錯誤。

綜上所述，通過運用數形結合的思想畫出函數圖象，可以將抽象的三角函數問題轉化成比較直觀的幾何圖形，這樣不僅可以幫助學生更容易地學習三角函數，還可以激發學生的學習興趣。