HIV在人體免疫網絡中傳播的動力學研究

黃 穎,婁 潔

獲得性免疫缺陷綜合癥(acquired immvne def i ciency syndrome,AIDS),也稱艾滋病,是由人類免疫缺陷病毒(human immunodef i ciency virus,HIV)引起的惡性傳染病.目前,AIDS已是一個全球性的公共衛生問題.研究發現,接受高效聯合抗逆轉錄病毒療法(highly active antire trorival therapy,HAART)的HIV患者的共同特征是持續低水平的病毒血癥[1].這就提出了一個重要的問題:是否某些組織具有某種特殊生理結構,如大腦中的血腦屏障或睪丸中的血睪屏障,使得大部分的藥物無法穿透屏障,從而導致它們成為患者在接受治療期間病毒持續產生的儲存庫,或稱HIV病毒的避難所[1].

HIV病毒的靶細胞是淋巴細胞,而淋巴細胞能夠在淋巴組織和非淋巴組織之間再循環.再循環是一個復雜的過程.簡言之,淋巴細胞從血液進入淋巴結或粘膜淋巴組織,然后再次回到血液,穿過隔離系統形成免疫監視和免疫功能的基礎.當遇到抗原,靜息的淋巴細胞被激活,并大量復制.激活的淋巴細胞從脾臟和淋巴結進入血液,然后再從血液進入其他的淋巴組織和非淋巴組織,對抗原實施殺傷作用.

在淋巴組織和血液中,感染的細胞會產生大量的HIV感染性病毒顆粒[2-3].一旦個體被感染,HIV病毒就會通過血液循環進入到身體各處.由于血液中病毒易于檢測,通常衛生部門會通過血液中的HIV濃度來量化感染者體內的病毒載量情況.由于大部分組織中的病毒載量難以檢測,血液中的病毒載量能否準確地說明其他組織中的病毒載量尚無定論.研究發現,接受抗病毒治療時,血漿病毒水平較低或幾乎檢測不到[4-5],而通過細胞培養或聚合酶鏈式反應(polymerase chain reaction,PCR)技術仍然在精液中發現了病毒的存在.這表明,一些藥物無法穿透血睪屏障并降低感染者傳播HIV的能力[6-7].因此,許多感染個體的外周血自由病毒的水平并不能正確地反映身體內正在發生的狀況[6].

本工作旨在探討大腦等器官是否為HIV病毒的儲存庫,以及血液中HIV的濃度能否代表身體其他組織的病毒水平.

1 模型

Callaway等[8]提出了HIV病毒動力學模型,考慮了兩個組織間的病毒傳播問題.但考慮到淋巴細胞再循環,尤其是體內不同的淋巴組織、血液和大腦(或睪丸)等組織構成的網絡,本工作建立了一個改進的HIV病毒動力學模型,描述了各淋巴細胞以及HIV病毒在體內網絡中的分布情況.模型假設如下:對于第i個器官(組織、血液、睪丸或大腦),Ti表示易感的CD4+T細胞,表示已經被HIV感染的T細胞,表示慢性感染T細胞,Vi表示HIV病毒載量,則在HAART下各類細胞和病毒的動力學方程為

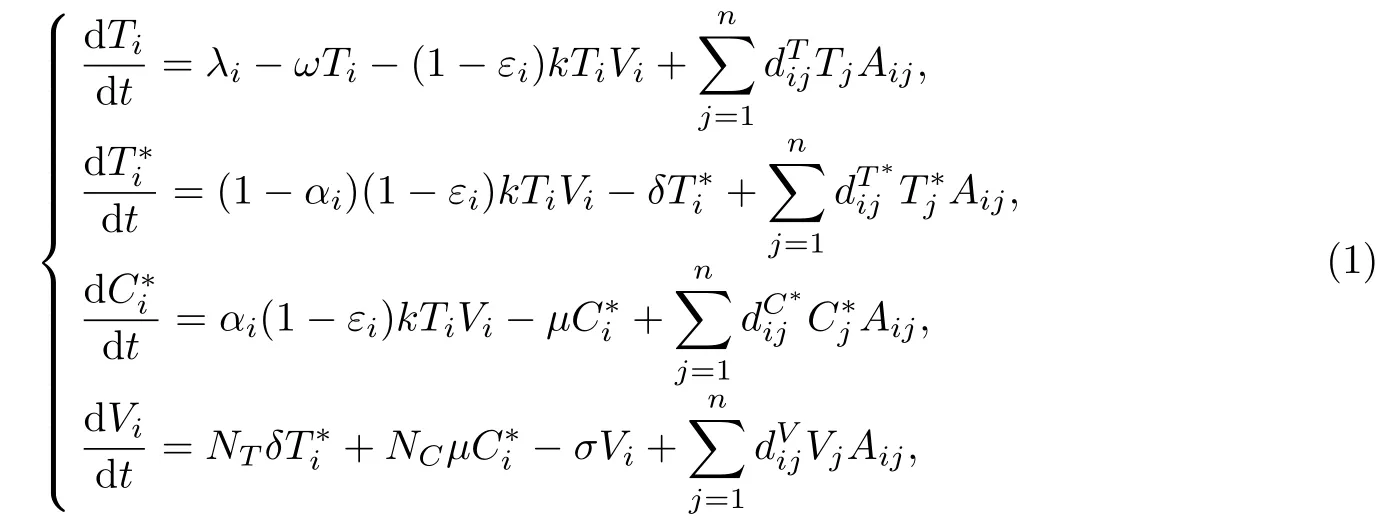
式中:i=1,2,···,n,n=200,并約定i=1表示血液系統,i=200表示大腦系統,其他表示組織,如淋巴結、脾臟等;常數λi表示易感細胞的來源,ω為死亡率,常數k為感染率,αi為感染細胞變為記憶感染細胞的比例;常數μ為記憶感染細胞死亡率,δ為感染細胞的死亡率;NT,NC分別為T?和C?產生病毒顆粒的平均數量;σ是病毒清除率,εi表示藥物效果,0≤εi≤1;分別表示T,T?,C?和V細胞從i到j的傳播率,為了方便起見,簡寫為dT,dT?,dC?,dV.細胞和病毒在血液、組織和大腦之間的傳播受常數dT,dT?,dC?和dV以及矩陣A影響.A=G?M表示允許傳播交換,其中G是傳播網絡的鄰接矩陣,如果細胞或病毒被允許從j到i,則定義Gij=1,對角矩陣M為移出矩陣,忽略傳播過程中病毒或細胞的出生率和死亡率,矩陣G和M分別為

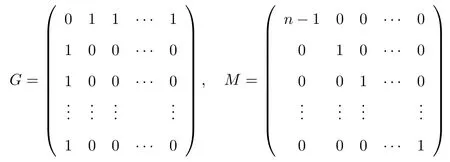
2 理論結果

為了找到模型(1)的無病平衡點,考慮

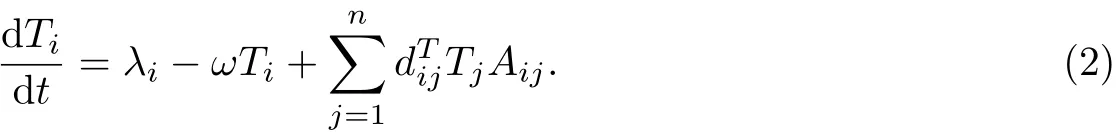
式(2)可改寫為

式中,T=(T1,T2,···,Tn)T,λ =(λ1,λ2,···,λn)T,矩陣Θ 為

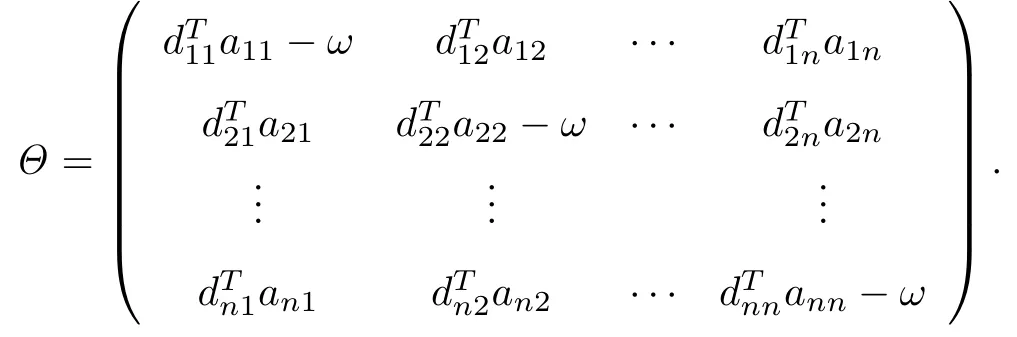
顯然,模型(2)存在正平衡點~T,且有

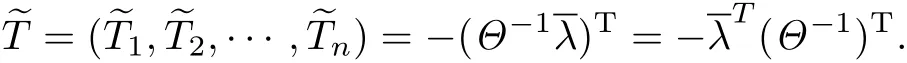
如果矩陣Θ的所有特征值均具有負實部,則容易證明正平衡點~T是局部漸近穩定的,即有

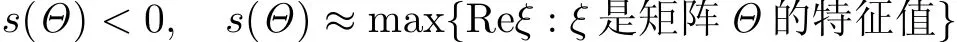
成立.

模型(1)有唯一的無病平衡點E0=(~T,0,0,0),這里0表示n維零向量.

對于無病狀態E0,線性化模型(1)中的感染類T?,C?,V可表示為

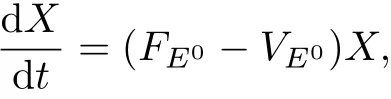
式中:

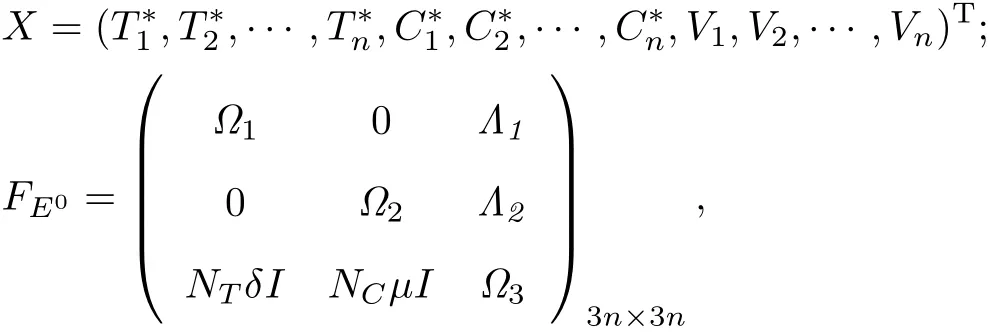
其中I是n×n的單位矩陣,且有

利用“再生矩陣”方法[9],可求得基本再生數R0,

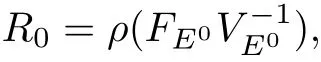
定理1 當s(Θ)＜0時,若R0＜1,則無病平衡點E0是局部漸近穩定的;若R0＞1,則E0是不穩定的.

定理1表明:當R0＜1時,個體內的HIV-1不會持續存在;反之,感染將持續存在.

3 數值模擬

由于不同個體內的參數值不確定,需對每一個參數使用拉丁超立方體(Latin hypercube)抽樣[10],給定每個不確定參數的概率密度函數.本工作共模擬500次Latin hypercube抽樣.

表1為改進的HIV病毒動力學模型的參數.按照表1給出的參數范圍,500次Latin hypercube抽樣下的基本再生數R0的均值為2.28(標準差:1.85;95%置信區間:2.04～2.51;四分位區間:1.11～2.78),表明即使感染個體接受有效的抗逆轉錄病毒療法(antiretroviral therapy,ART),基本再生數R0也不可能小于1,即病毒無法從該個體內徹底清除.

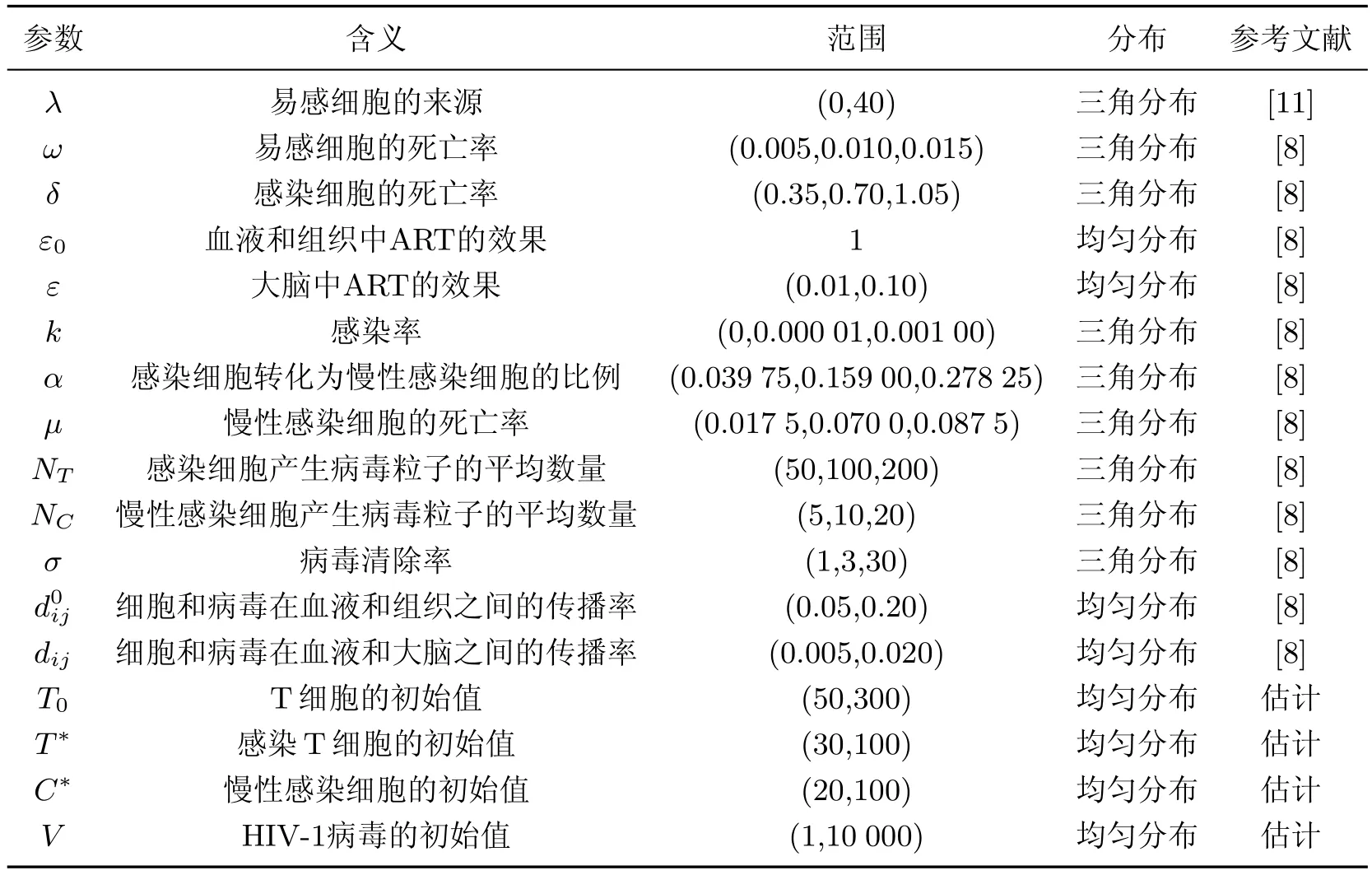
表1 改進的HIV病毒動力學模型的參數Table 1 Parameters of improved HIV virus dynamic model

假設在血液和組織中ε0=1,即藥物療效為100%,病毒復制被完全抑制.考慮到血腦屏障的存在,大腦中的ε在(0.01,0.10)內取值,其他參數取值見表1,則感染個體接受治療后血液和大腦中健康T細胞和病毒載量的濃度變化分別如圖1～2所示.

由圖1可以看出:ART治療后,血液中健康CD4+T細胞的平均濃度減少,但隨時間增加,濃度逐漸增大,兩個月后達到480.0 Cells/mL;大腦中T細胞的平均值變化與CD4+T細胞類似,但是比血液低很多,最終為345.0 Cells/mL.淋巴組織中健康CD4+T細胞的平均濃度隨時間增大,最終達到546 Cells/mL,比血液中高很多.因此,血液中淋巴細胞狀況并不能體現它們在其他組織或器官中的狀況.

圖1 感染個體治療后血液和大腦中健康T細胞的濃度變化Fig.1 Concentraion of healthy T cells of HIV patients after ART in blood and in brain respectively

由圖2可以看出,血液中病毒載量的平均濃度在治療的初期按指數規律衰減,隨著時間的增加,衰減的速度減慢,組織中病毒載量的平均濃度呈現類似的趨勢.但是大腦內病毒載量的平均濃度的變化趨勢與血液和其他組織不同,在初始的3周內病毒載量的平均濃度逐漸減小,隨后卻呈現增大態勢,且最終穩定在一個較高的水平,平均約為84.3Cells/mL,比血液和組織中的HIV載量高得多.上述結果表明,外周血自由病毒水平并不能正確反映身體內其他組織中的狀況[1].

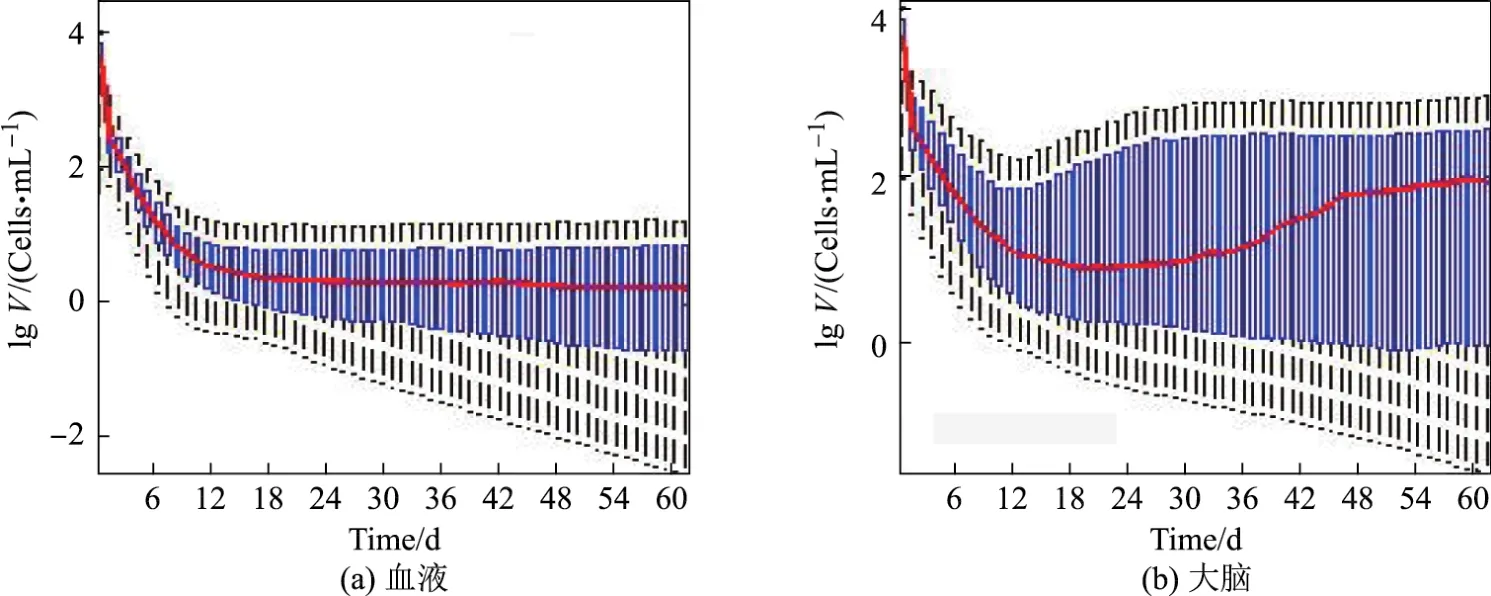
圖2 感染個體治療后血液和大腦中病毒載量的濃度變化Fig.2 Concentraion of of HIV virus of HIV patients after ART in blood and in brain respectively

4 討論

Perelson等[12]研究了8個接受ART治療的HIV感染者,研究結果發現,患者呈現的病毒衰變模式如下:治療初期,病毒呈現快速指數衰減態勢;接下來則呈現較慢的指數衰減.本工作發現了與之類似的規律.顯然,在血液和組織中,接受2周治療的患者的血漿病毒血癥低于標準檢測閾值50拷貝/mL,但大腦內的病毒載量最終會維持在一個較高的水平.這表明在常規檢查中,即使外周血中的病毒水平已經檢測不出,也不能隨意停止HAART的治療,以免個人免病毒載量發生反彈,導致耐藥株產生并在宏觀人群中傳播.

[1]SHEN L,SILICIANO R F.Viral reservoirs,residual viremia,and the potential of highly active antiretroviral therapy to eradicate HIV infection[J].Journal of Allergy and Clinical Immunol,2008,122(1):22-28.

[2]PERELSON A S,ESSUNGER P,CAO Y,et al.Decay characteristics of HIV-1-infected compartments during combination therapy[J].Nature,1997,387(6629):188-191.

[3]HAASE A T,HENRY K,ZUPANCIC M,et al.Quantitative image analysis of HIV-1 infection in lymphoid tissue[J].Science,1996,274(5289):985-989.

[4]HAMED K A,WINTERS M A,HOLODNIY M.et al.Detection of human immunodef i ciency virus type 1 in semen:eあects of disease stage and nucleoside therapy[J].Journal of Infectious Diseases,1993,167(4):798-802.

[5]VERNAZZA P L,ERON J J,COHEN M S,et al.Detection and biologic characterization of infectious HIV-1 in semen of seropositive men[J].AIDS,1994,8(9):1325-1329.

[6]LEVY J A.HIV and the pathogenesis of AIDS[M].3rd ed.Washington:ASM Press,2007.

[7]BARkER C F,BILLINGHAM R E.Immunologically privileged sites[J].Advances in Immunology,1978,25:1-54.

[8]CALLAWAY D S,PERELSON A S.HIV-1 infection and low steady state viral loads[J].Bulletin of Mathematical Biology,2002,64(1):29-64.

[9]Van Den DRIESSCHE P,WATMOUGH J.Reproduction numbers and sub-threshold endemic equilibrium for compartmental models of disease transmission[J].Mathematical Biosciences,2002,180(1/2):29-48.

[10]BLOWER S M,GERSHENGORN H B,GRANT R M.A tale of two futures:HIV and antiretroviral therapy in San Francisco[J].Science,2000,287(5453):650-654.

[11]LOU J,LOU Y J,WU J H.Threshold virus dynamics with impulsive antiretroviral drug eあects[J].Journal of Mathematical Biology,2012,65(4):623-652.

[12]PERELSON A S,ESSVNGER P,CAO Y,et al.Decay characteristics of HIV-infected compartments during combination therapy[J].Nature,1997,387(6629):188-191.