鉸鏈四桿機構的急回特性分析

龐立軍

摘要：最近幾年，在給學生講解鉸鏈四桿機構的急回特性時，我才用了項目引導教學法，用實際例子，給出任務，指導學生按照講述內容的思路，動手實做，逐步畫出分析的機構，整個過程要求學生耐心、仔細，控制作圖誤差在允許的范圍內。任務驅動，學生感到更充實，把學生摁在座位上，踏踏實實地完成任務，取得了較好的效果。

關鍵詞：鉸鏈四桿機構;極限位置;極位夾角;行程速比系數

鉸鏈四桿機構的急回特性是其重要的運動特性，它是通過機構的極位夾角和行程速比等參數反映出來的。所以，研究四桿機構的急回特性，是設計機構應用的重要知識點，全面系統的解析是我們教學工作的重要任務。下面就我在教學實施過程中的思路和過程進行闡述。

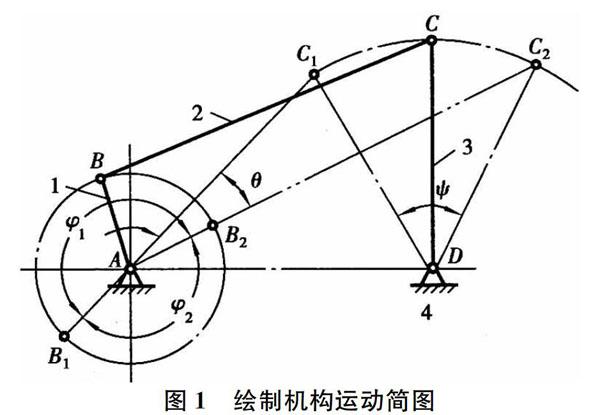
1 繪制機構運動簡圖

進行急回特性的分析，要把問題落實到實際機構中，因此，首先給出相應尺寸，繪制鉸鏈四桿機構的運動簡圖，帶著學生進行定量分析。如圖所示，該機構由4個桿，用4個鉸鏈連接而成，四個桿的長度分別為LAB=20mm，LBC=60mm，LCD=40mm，LAD=50mm，接下來需要判斷其類型。四個桿的長度滿足長度和條件，最短桿為連架桿，所以最短桿AB為曲柄，桿CD為搖桿，該機構為曲柄搖桿機構。現在明確思路，畫出該機構的運動簡圖，過程如下，在作圖平面上畫出水平線段AD，標注固定符號，設定為機架，以A點為圓心20mm為半徑畫出圓周，表明曲柄上的B點運動軌跡是該圓周，在圓周上任意確定一點B。連接AB，確定曲柄的一個任意位置，當曲柄位置確定以后，連桿BC和搖桿CD的位置相應就確定了，關鍵是找到C點，以D點為圓心40mm為半徑畫出C點運動軌跡圓弧，C點的運動軌跡是該圓弧的一段曲線，也就是說C點在這個圓弧上，再以B點為圓心60mm為半徑畫另一段圓弧，那么，兩圓弧的焦點就是C點的位置，連接B點和C點，連接C點和D點，用鉸鏈簡單符號表示4個桿的連接處，就得到了該鉸鏈四桿機構的機構運動簡圖。曲柄整周連續轉動，可以到達360度任何一個位置，搖桿在擺角范圍內來回擺動，存在左右兩個極限位置。因此，需要確定搖桿的擺動范圍，確定搖桿的兩個極限位置。機構在運動過程中，曲柄和連桿有兩次共線的位置，當重疊共線時，搖桿處于最左端，展開共線時搖桿處于最右端。所以，以A點為圓心40mm為半徑，畫圓弧與C點軌跡圓弧的交點為C1，連接C1D，此處就是搖桿的左端極限位置，連接C1A延長到B點圓周交點為B1，AB1C1D就是該曲柄搖桿機構左邊極限位置的形狀。然后，以A點為圓心，80mm為半徑畫圓弧，該圓弧與C點軌跡圓弧的交點為C2，連接C2D，此處就是搖桿的右端極限位置，連接C2A， C2A與B點軌跡圓周的交點為B2，AB2C2D就是該機構在最右端極限位置形狀。現在就展示出曲柄搖桿機構的三個位置，一個一般位置，左右兩個極限位置，C1D和C2D夾角為搖桿的行程擺角Ψ，AC1和AC2夾角θ為該機構的極位夾角。用量角器可以測量擺角θ和極位夾角Ψ。

2 急回特性的分析

設曲柄AB為原動件，則原動件AB在轉動一周過程中，有兩次與連桿BC共線，共線位置為AC₁和AC₂。鉸鏈中心A與C之間的最短距離為AC₁，最長距離為AC₂，所以，C₁D和C₂D分別是從動搖桿CD向左和向右擺動的兩個極限位置。對應于搖桿處于兩極限位置時曲柄所在AB₁和AB₂兩位置之間所夾的銳角θ稱為極位夾角。

當曲柄以等角速度ω順時針轉過角φ₁時，搖桿由位置C₁D擺動到C₂D（工作行程），擺角為Ψ，所需時間為t₁，搖桿CD擺動的平均角速度為ω_m1。當曲柄繼續轉過角φ₂時，搖桿由位置C₂D擺動到C₁D（空回行程）擺角仍為Ψ，所需時間為t₂，搖桿的平均角速度為ω_m2。由圖可知，曲柄所對應的兩個轉角φ₁和φ₂分別為：φ₁=180°+θ，φ₂=180°-θ。由于φ₁>φ₂，因此曲柄以等角速度ω轉過這兩個角度時，對應的時間t₁>t₂，且φ₁/φ₂= t₁/t₂。搖桿CD的平均角速度為ω_m1=Ψ/t₁，ω_m2=Ψ/t₂，顯然，ω_m1<ω_m2。由此可見，當曲柄等速轉動時，做往復運動的搖桿在空回行程的平均速度大于工作行程的平均速度，這一性質稱為四桿機構的急回特性。機構的急回特性用ω_m2和ω_m1的比值K來表示，它說明機構的急回程度，通常將K稱為行程速比系數。

若已知K，即可求得極位夾角θ為

公式表明，機構的急回程度取決于極位夾角θ的大小。只要θ≠0°，總有K>1，機構具有急回特性;θ角越大，K值也越大，機構的急回特性也越明顯。當θ=0°時，K=1則機構無急回特性。