鏈式多邊形與三角形的穩定性的理想模型

☉湖北省武漢科學技術館 張忠斌

一直以來，在數學詞典中都找不到三角形的穩定性的確切定義，現有各種版本的教材中給出的描述性定義也不統一，同時，給出的實驗模型也比較粗糙.本文擬提出鏈式多邊形，并以此構建一種有關三角形的穩定性的理想模型，或可對認識這一問題有所幫助.

一、教材中三角形的穩定性描述

三角形的穩定性一直是初中幾何的一個教學內容.它早期出現在上海人民出版社1973年版《幾何》［1］.內容如下：

我們先來做一個實驗：用木條釘一個三角形和一個四邊形的架子，如果拉動這兩個架子，就會發現三角形架子的形狀始終不變，而四邊形架子的形狀可以改變.這個事實說明，三角形具有一種使結構不變的性質，我們把這種性質叫做三角形的穩定性.由于三角形具有穩定性，采用三角形結構，就能增加物體的堅固程度，而且又節約了材料，因此它在生產實踐中被廣泛地采用.

由吉林工業大學數學教研室編的1973年版《幾何》［2］，對三角形的穩定性的表述如下：

由定理3，我們知道一個三角形如果三邊固定下來，那么這個三角形的形狀就隨之固定下來了，就是說，外力不改變三角形的形狀，這就是所謂的三角形的穩定性.

筆者讀初中所用的幾何課本是人教版1981年版《幾何》［3］.有關三角形的穩定性的內容與上述表述相當，只是多畫了兩幅示意圖.內容如下：

邊邊邊公理表明，只要三角形三邊的長度固定，這個三角形的形狀和大小就完全確定.例如，取三條長度適當的木條，用釘子把它們釘成一個三角形，所得到的三角形的形狀和大小就固定（圖1）.三角形這個性質叫做三角形的穩定性.這是三角形特有的性質.其他多邊形就沒有這種特性.例如，把四條長度適當的木條訂成一個四邊形的架子，它的形狀是可以改變的（圖2）.

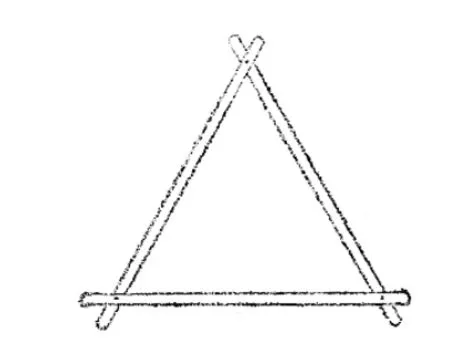
圖1

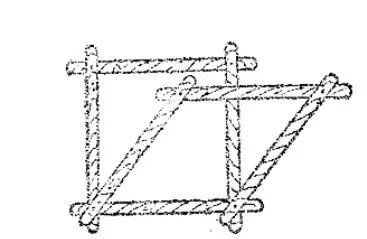
圖2

最新版本的人教版2013年版八年級《數學》［4］也有關于三角形的穩定性知識點.該書沒有給出三角形的穩定性定義，但卻得出了如下的一些提問和結論：

如圖3（1），將三根木條用釘子釘成一個三角形木架，然后扭動它，它的形狀會改變嗎？

如圖3（2），將四根木條用釘子釘成一個四邊形木架，然后扭動它，它的形狀會改變嗎？

如圖3（3），在四邊形木架上在釘一根木條，將它的一對不相鄰的頂點連接起來，然后扭動它，這時木架的形狀會改變嗎？為什么？

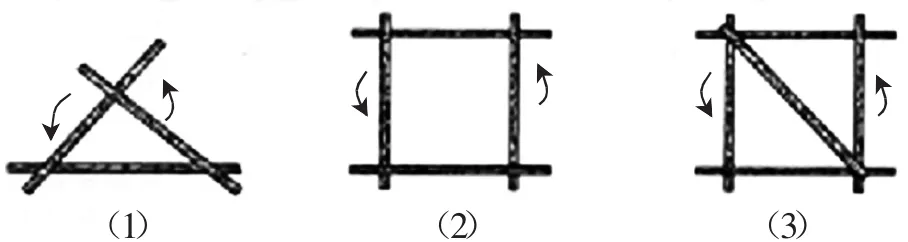
圖3

可以發現，三角形木架的形狀不會改變，而四邊形木架的形狀會改變.這就是說，三角形是具有穩定性的圖形，而四邊形沒有穩定性.

上述“用木條釘一個三角形和一個四邊形的架子”，這個驗證三角形的穩定性的實驗模型顯得很粗糙；一是釘子與木條是否都垂直，二是釘子與木條之間必定有很大的摩擦力，三是木條與木條之間也有一定的摩擦力.這三個因素都會阻礙木條的旋轉，于是就造成了操作時需要“拉動”，從而看起來像力學實驗一樣，容易造成幾何與力學的理解上的混亂.這個不良模型需要改進.

二、鏈式多邊形及三角形的穩定性的理想模型

為了討論三角形的穩定性，有必要引入旋轉點和鏈式多邊形概念.關于旋轉點，可以從角的動態定義和圓的一個定義中找到.一條射線繞著它的端點從一個位置旋轉到另一個位置所形成的圖形叫做角.所旋轉射線的端點叫做角的頂點.當一條線段繞著它的一個端點在平面內旋轉一周時，它的另一個端點的軌跡叫做圓.

借此可以定義旋轉點.空間上具有旋轉特性的點，叫做旋轉點.采用同心圓“ ”表示，內圓表示旋轉點，外圓表示旋轉；或者借用圓心符號“⊙”來表示，內中的點表示旋轉點，外圓表示旋轉.上述角的頂點和圓心都是旋轉點.以下分別用“ ”和“⊙”表示角的頂點和角.如圖4所示.

圖4

這個圖形看起來像鐘表的兩個指針，可以繞軸旋轉.也就是，頂點為旋轉點的角，其角度不是固定不變的.

由端點為旋轉點的線段組成的多邊形叫做鏈式多邊形.那么，在所有的鏈式多邊形中，只有三角形的形狀是不變的.下面用旋轉點組成鏈式三角形和鏈式四邊形，旋轉點用“⊙”表示.如圖5所示.

圖5

比較圖4中的角和圖5中的鏈式三角形，可以看出，如果讓頂點為旋轉點的角固定不變，可以連接這個角的兩條邊組成一個三角形，那么這個角就不會再改變了.實際中，將人字梯的兩個支撐梯的橫檔用一根繩子的兩端分別系住，展開繃緊，人字梯就穩固了；一些圓規的設計也采用了這種原理.

下面筆者結合鏈式多邊形提出較為理想的實驗模型.

三角形的穩定性的實驗模型：在光滑合適的木條兩端分別鉆直徑相等的孔，在木條與木條之間配上減少摩擦力的墊圈，再用相當尺寸的銷子適當鎖定，組成鏈式三角形和鏈式四邊形.如圖6所示.

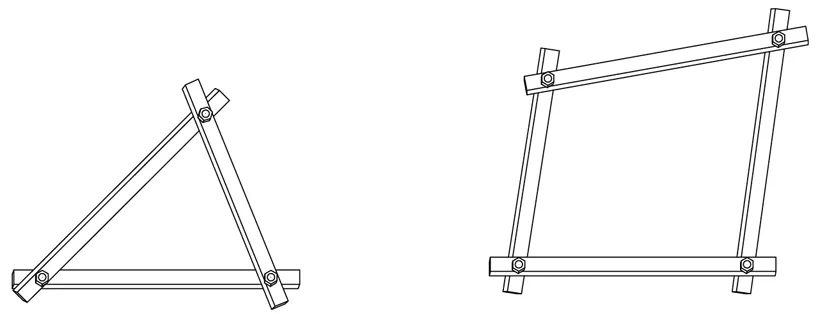
圖6

這里鉆的孔和銷子所組成的結構就相當于旋轉點的結構.輕輕撥動這兩個木架，會發現三角形木架的形狀始終不變，而四邊形木架的形狀可以改變.也就是說，在鏈式多邊形中，只有鏈式三角形的形狀固定不變.鏈式三角形的這種性質叫做三角形的穩定性.

如果將鏈式四邊形的一條對角線連接起來，組成兩個鏈式三角形，這樣的圖形其形狀也固定不變.這一點體現在理想實驗模型上，則是用木條代替對角線，鉆孔鎖定.如圖7所示.

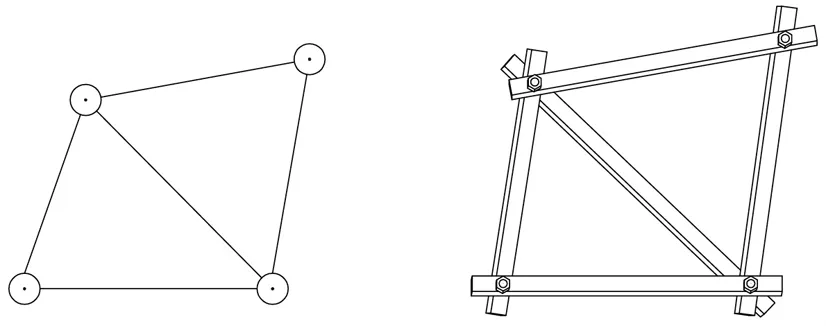
圖7

三、結束語

三角形的穩定性同三角形的確定性［5］“給定三邊，則三角形唯一確定”命題有所聯系.另外，三角形的穩定性也可以同余弦定理相聯系：已知三角形的三邊，根據余弦定理可以計算出三角形三個角的度數.也就是說，給出三角形的三條邊，那么這個三角形的三個角都可以計算出來，相當于這三個角也都給出了，從而鏈式三角形的形狀固定不變.

三角形的穩定性問題主要是特殊圖形的形狀是否存在不變性的問題，這類特殊圖形可稱之為鏈式多邊形.本文得到的結論是：在鏈式多邊形中，只有鏈式三角形的形狀固定不變而具有穩定性.

1.《初等數學》編寫組.《幾何》［M］.上海人民出版社，1973.

2.吉林工業大學數學教研室編.《幾何》［M］.吉林工業大學，1973.

3.中小學數學編輯室編.《幾何》（第一冊）［M］.人民教育出版社，1981.

4.課程教材研究所等編著.《數學》（八年級上冊）［M］.人民教育出版社，2013.

5.張忠斌.三角形的確定性問題探究［J］.中學數學（初中版），2017（5）.