PA 6/PET扁平復合纖維界面分布的數值模擬

葉 賀，潘 俊，張榮根，馮 培*，楊崇倡,

(1.東華大學 機械學院，上海 201620； 2.紡織裝備教育部工程研究中心，上海 201620)

復合異形纖維紡絲成形過程中，熔體間界面位置分布穩定性是影響復合異形纖維成形質量的關鍵因素[1]。當兩種聚合物熔體在異形微孔流道內流動時，不同的微孔結構參數和紡絲工藝參數會使兩種聚合物熔體流動速度和壓力產生差異，導致紡絲過程產生不穩定層流，界面位置分布不穩定，導致紡絲時絲條產生扭曲、粘板等現象。

復合纖維的紡絲成形過程中，熔體界面分布的研究大多聚焦于研究聚合物材料、流變特性以及溫度對界面分布的影響[2-4]，且傳統復合纖維的紡絲成形研究[5-7]通常忽略熔體的壁面滑移效應，而在實際紡絲中，噴絲板扁平微孔的長寬比(W/H)、微孔深度(L)以及熔體流量比對纖維成形也具有重要的影響，且壁面滑移的影響不可忽略。因此，作者以聚對苯二甲酸乙二醇酯(PET)和聚己內酰胺(PA 6)為例，分析兩種聚合物熔體在復合噴絲板扁平孔道內流動，在動力學數學模型的基礎上，考慮壁面滑移這一彈性行為，進行數值模擬，研究扁平微孔的W/H、L以及熔體流量比對復合熔體PA 6和PET界面位置分布的影響。

1 數值方程及模擬參數的設定1.1 紡絲動力學數學模型

理論狀態下，復合異形纖維成形過程遵循三大守恒的基本定律，假定熔體不可壓縮的前提下，忽略慣性項、絲條重力的影響。其能量方程、動量方程、連續性方程分別如式(1)，(2)，(3)所示。

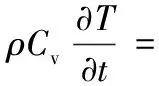
(1)

η▽2V-▽P=δ/R

(2)

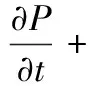
(3)

式中：ρ為密度；t為時間；V為速度矢量；Cv是熔體的體積熱容；T為溫度；K為熱傳導率；τ為應力張量；P為壓力；η是黏度；δ為表面張力；R為高斯曲率。

1.2 滑移因子的確定

參照Mooney[8]的方法研究壁面滑移行為：在熔融紡絲過程中，考慮壁面滑移這一彈性行為，假定聚合物熔體不可壓縮且為穩態層流，則在扁平微孔中，其滑移速度方程、扁平微孔流量方程以及形狀因子方程分別如式(4)，(5)，(6)所示。

Vs=θξm

(4)

(5)

(6)

式中：Vs為滑移速度；θ為滑移系數；m為冪律指數；ξ為壁面處的剪切應力；W為扁平微孔長度；H為扁平微孔寬度；Q為單孔體積流量；Fq為形狀因子；i為1，3，5....；h為函數變換系數。

一般而言，扁平微孔中，W/H大于10，其Fq小于1，故當其在同樣體積流量下,與常規矩形微孔形狀相比，扁平孔道中聚合物熔體流動時需要的壓力降更高。參照汪春[9]所做壁面滑移研究，PET和PA 6熔體的θ分別取為1.5，1.2。

1.3 幾何模型

建立幾何模型，如圖1所示。BS1為PET入口；BS2為PA 6入口；BS3為噴絲孔壁面；BS4為PET與PA 6交界面； BS5為自由面(纖維表面)。

圖1 扁平微孔幾何模型Fig.1 Geometric model of flat microhole

1.4 模擬參數的設定

模擬參數包括材料物性參數和模擬紡絲工藝參數，見表1和表2。其中，n為非牛頓指數，λ為松弛時間，η0為零切黏度，Cp為熱容量，T1為紡絲入口溫度，T2為紡絲冷卻溫度。

表1 材料物性參數Tab.1 Physical index of feedstocks

表2 模擬紡絲工藝參數Tab.2 Simulated spinning process parameters

1.5 邊界條件

數值模擬時，設定以下邊界條件：兩種流體的流動沒有穿透界面；界面之間沒有相對滑移；界面上兩種聚合物熔體切向速度相同；兩側切向應力張量相等；孔道邊界添加滑移系數；流動出口設定作用零法向力和零切向力。

1.6 數值模擬計算

(7)

式中：η∞為無窮零切黏度。

有限元數值計算的迭代算法為Pi-card迭代算法，速度采用Mini-element線性插值,微孔部分設置3D網格重置。

2 結果與討論

2.1 微孔W/H對界面位置分布的影響

為研究噴絲板微孔W/H對界面位置的影響，在Q為3.2×10-7m3/s、PET:PA 6流量比為1:1不變的情況下，噴絲板微孔L為1.5 mm，噴絲板微孔W/H根據工廠經驗分別設置為10,11,12,13，研究熔體流動過程中的界面位置分布規律，計算結果如圖2所示。本文中的界面位置偏移量是指PA 6和PET的界面位置偏移量；偏移量為正，代表PET一側偏向PA 6一側，偏移量為負，代表PA 6一側偏向PET一側；界面相對偏移量可理解為整體變化趨勢。

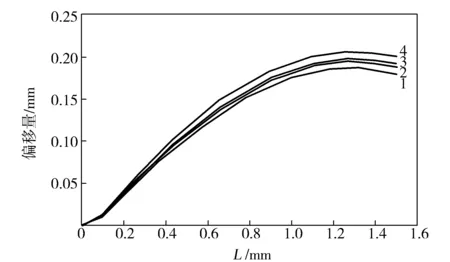
圖2 不同W/H時噴絲板孔道內界面位置分布Fig.2 Interface position distribution in spinneret hole with different W/H ratioW/H：1—10；2—11；3—12；4—13

由圖2可知，界面偏移量為正，表示PA 6/PET扁平復合纖維界面由PET一側偏向PA 6一側。在一定范圍內，W/H的不同僅對熔體界面位置產生一定的影響，而對相對偏移量沒有產生影響，即隨著W/H增大，界面位置偏移量逐漸增大。

由圖3可以發現，噴絲板W/H的變化對熔體兩側壓力分布影響不大。故噴絲板微孔W/H的變化主要影響到熔體界面位置偏移量的分布。

圖3 不同W/H時熔體的等壓線分布Fig.3 Isopiestic distribution of melt at different W/H ratio

2.2 微孔L對界面位置分布的影響

為研究微孔L對界面位置的影響，在Q為3.2×10-7m3/s、PET:PA 6流量比為1:1不變的情況下，噴絲板微孔W/H設定為10，分別將微孔L設置為1.2，1.5，1.8，2.0 mm，研究不同L對界面位置分布的影響，結果如圖4所示。

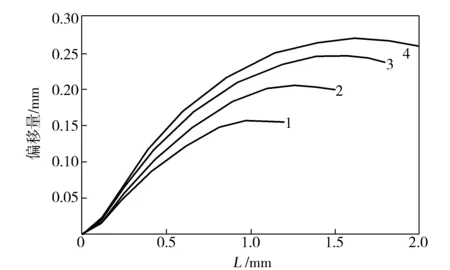
圖4 不同L時噴絲板孔道內界面位置分布Fig.4 Interface position distribution in spinneret holes with different LL：1—1.2 mm；2—1.5 mm；3—1.8 mm；4—2.0 mm

由圖4可知，界面偏移量為正，表示PA 6/PET扁平復合纖維界面由PET一側向PA 6一側偏移。不同的L影響熔體在孔道內流動時的界面分布位置，隨著噴絲板L的增大，熔體界面位置偏移量逐步增大，界面相對偏移量也逐步增大。

通過圖5對比不同L時熔體的等壓線分布可知，熔體兩側壓力分布相對均勻，同一截面處壓力差別不大。

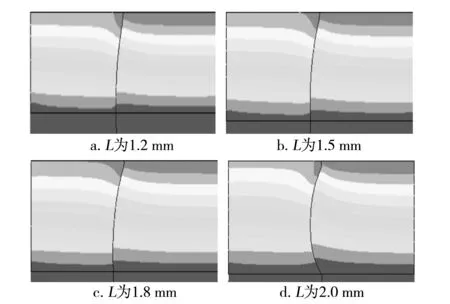
圖5 不同L時熔體的等壓線分布Fig.5 Isopiestic distribution of melt at different L

2.3 流量比對界面位置分布的影響

為研究流量比對界面位置的影響，在Q為3.2×10-7m3/s，W/H為10，L為1.5 mm，紡絲溫度設定在290 ℃時，設定不同的PET/PA 6流量比。PA 6:PET流量比為1:1，1:2，1:3，2:1，3:1進行數值模擬，計算結果如圖6所示。

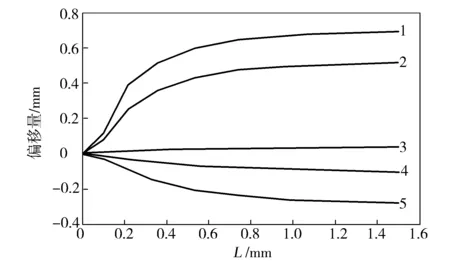
圖6 不同PA 6/PET流量比時噴絲板孔道內界面位置分布Fig.6 Interface position distribution in spinneret hole at different PA 6/PET flow ratioPA6:PET流量比：1—1:3；2—1:2；3—1:1；4—2:1；5—3:1

由圖6可知，偏移量為正時，表示熔體界面偏向于PA 6一側，當其為負時，表示熔體界面偏向于PET一側。復合紡絲時，不同的PA 6/PET流量比會對熔體界面的分布產生較大的影響，會導致噴絲板孔道內熔體界面發生偏移，流量比對噴絲板孔道內的熔體界面的相對偏移量影響較小，但是其對熔體界面位置分布影響巨大。

由圖7可以看出，當PET:PA 6流量比為1:1時，界面兩側的剪切流動基本呈對稱分布，此時的界面偏移主要是由于PET/PA 6的流動特性差異造成的，即PET流動性差于PA 6流動性，導致界面偏向于PA 6一側；當PET:PA 6流量比為2:1時，界面位置偏向于PET一側，原因是PET流量增大時，根據非牛頓流體的剪切變稀特征，界面兩側的剪切速率差值增大，熔體黏度差異增加，引起界面偏移增大，此時界面偏移主要由PET流量的加大導致界面兩側差異的增大造成，此時流量比對界面分布的影響大于材料特性對界面分布的影響。隨著PA 6/PET流量比的增大，熔體界面位置偏移量由PA 6一側逐步減小至PET一側反向逐步增大；通過圖6對比其等壓線分布可知：同一截面處的壓力差異隨著PA 6/PET流量比的增大而逐步減小至反向增大。

圖7 不同PA 6/PET流量比時熔體的等壓線分布Fig.7 Isopiestic distribution of melt at different PA 6/PET flow ratios

3 結論

a. 在一定范圍內，隨著W/H值的增大，界面位置偏移量逐漸增大，相對偏移量沒有變化；噴絲板W/H的變化對同一截面處熔體兩側壓力分布差異影響不大。

b. 不同的噴絲板L影響扁平熔體在孔道內流動時的界面分布位置，隨著噴絲板L的增大，熔體界面位置偏移量逐步增大，界面相對偏移量也逐步增大；但熔體兩側壓力分布相對均勻，同一截面處壓力差異不大。

c. 當總流量不變的情況下，不同的PA 6/PET流量比對界面偏移量的影響很大，隨著PA 6/PET流量比的增大，熔體界面位置偏移量由PA 6一側逐步減小至PET一側反向逐步增大；同一截面處的壓力差異隨著PA 6/PET流量比的增大而逐步減小至反向增大。合理的流量比能夠減小界面偏移量，改善紡絲時復合扁平纖維的成形效果。

d. 扁平纖維界面分布的數值模擬對與PA 6:PET物性指標類似的其他高聚物的復合紡絲具有指導意義。

參 考 文 獻

[1] 紀占國.分層界面滑移對聚合物共擠成型過程影響的數值模擬研究[D].南昌:南昌大學,2008．

Ji Zhanguo.The numerical simulation on influence of interfacial slipping on polymer co-extrusion molding process[D].Nanchang：Nanchang University，2008.

[2] Han C D, Shetty R.Studies on multilayer film coextrusion. I. The rheology of flat film coextrusion[J]. Polym Eng Sci,1976,16(10):697-705.

[3] Puissant S, Vergnes B, Demay Y, et al. A general non-isothermal model for one-dimensional multilayer coextrusion flows[J]. Polym Eng Sci,1992, 32(3):213-220.

[4] Matsunaga K, Kajiwara T, Funatsu K. Numerical simulation of multi-layer flow for polymer melts-A study of the effect of viscoelasticity on interface shape of polymers within dies[J]. Polym Eng Sci,1998,38(7):1099-1111.

[5] 楊崇倡，譚志強，魏蕊,等.扁平纖維紡絲成形研究Ⅰ.扁平纖維紡絲成形的數字模型及模擬分析[J].合成纖維工業,2009,32(3):56-59.

Yang Chongchang,Tan Zhiyin,Wei Rui,et al. Study on flat fiber formation Ⅰ.Mathematical model and simulation analysis of flat fiber formation[J].Chin Syn Fiber Ind,2009,32(3):56-59.

[6] 呂洪，劉正恒，馬驛,等.PBT/PET 并列型復合紡絲的研究[J].合成技術及應用，1995，10(1)：8-14.

Lv Hong, Liu Zhengheng,Ma Yi, et al.Study on PBT/PET side-by-side conjugate spinning[J]. Syn Tech Appl,1995，10(1)：8-14.

[7] 張敏, 孫勝, 賈玉璽. 雙層聚合物共擠出過程的數值模擬[J].高分子材料科學與工程,2005,21(6):15-19.

Zhang Min, Sun Sheng, Jia Yuxi.Numerical simulation of double-layer polymer coextrusion process[J]. Polym Mater Sci Eng,2005, 21(6):15-19.

[8] Mooney M. Explicit formulas for slip and fluidity[J]. J Rheol,1931(2):210-222.

[9] 汪春. 紡絲成形過程中聚合物熔體壁面滑移的研究[D].上海:東華大學, 2016.

Wang Chun. Research on wall slip of polymer melt in spinning process[D].Shanghai:Donghua University, 2016.

[10] Gupta S, Uday V, Raghuwanshi A S, et al. Simulation of blow molding using Ansys Polyflow[J]. Apcb Proced, 2013,5:468-473.