初中數學從“知識課堂”到“探究課堂”的思考

江勤娟

[摘 要] 注重生本課堂的價值達成，就要將數學課堂由原先的“知識課堂”引領到“探究課堂”中. 我們不僅要從思想意識上全面轉變，更要從教學行為中真正落實到行動中，讓探究性學習落到實處，并將探究性思維滲透到學習行為中.

[關鍵詞] 探究；思維；遞進；初中數學

隨著素質教育的實施和推進，課堂教學模式也發生了翻天覆地的變化. 原來傳統的“知識課堂”正在向“探究課堂”轉變，這種轉變不再是因為上級教育主管部門要檢查，而是因為學生和教師在求知與教學過程中實實在在地需要. 在知識與技能的建構上，在問題與質疑的解決上，探究性思維與行為決定著學習的高度與深度，決定著學習的效果與價值. 因此，在這種探究性學習背景下，師生之間的地位變得越來越平等，學生的主體作用得以發揮. 但是，這種課堂模式的轉型并不是隨意就能完成的，而是需要師生之間共同配合，利用探究性教學活動，一步一步地實現探究課堂.

創設探究情境，激發探究欲望

在當前的教學模式下，情境教學法已經成為主要的教學方法之一. 為了能夠實現初中數學課堂向探究課堂的轉變，教師可以利用創設探究情境的方式，激發學生的探究欲望. 在科學、合理的教學情境中，學生的積極性能夠得到調動，情感狀態也能更加飽滿，對數學知識進行探究也會更有效率. 而教師則需要選擇合適的情境來迎合教學目標的達成，對接學生學習興趣的激發，引領學生思維的生長.

例如，筆者在開展“整式的加減”教學時，在數學課堂上設計了如下教學情境：

青藏鐵路線上，在格爾木到拉薩之間有一段很長的凍土地段. 列車在凍土地段的行駛速度是100千米/時，在非凍土地段的行駛速度可以達到120千米/時. 在西寧到拉薩路段，列車通過非凍土地段所需時間是通過凍土地段所用時間的2.1倍，如果通過凍土地段需要t小時，你能用含t的式子表示這段鐵路的全長嗎？

問題情境更能激發學生積極思考. 在筆者的引導下，學生進行思考和討論之后可以得到式子：100t+120×2.1×t. 通過這種創設探究教學情境的方式，既可以對同類項的概念進行學習，又能幫助學生建立符號感，體會整式的加減.

在良好的教學情境中，學生能夠對即將要學的數學知識產生探究興趣，這樣一來，便可以積極地發揮學生的主觀能動性，讓學生進行主動探究.

設置層次問題，循序漸進地探究

探究是一個過程，在這個過程中，學生應當遵循循序漸進的原則. 為了讓學生的探究過程更加順利，更加符合學生自身的心理認知特點以及發展規律，教師可以在課堂上設計一些層次性問題，由淺入深地引導學生循序漸進地進行探究. 在這種梯度性問題的引導下，探究也會一步一步地深入. 而這種梯度也不是一概而論的，教師要充分分析學生的學情和差異，結合學生的實際狀況進行調整，以此保障學生在其力所能及的范圍內達成思維的遞進.

筆者帶領學生學習“消元法解二元一次方程組”時，首先給出了這樣一道例題：籃球聯賽中，每場都要分出勝負，每隊勝1場得2分，負1場得1分，某隊10場比賽中得到16分，那么這個隊的勝、負場數分別是多少？設勝x場，負y場，根據條件，可列出二元一次方程組x+y=10①，2x+y=16②. 隨后，筆者提出了第一個問題：你能發現方程組中的兩個式子有什么聯系嗎？經引導，學生發現兩個式子中都含有y，由此可以由一個方程得到y的表達式，并把它代入另一個方程，變二元為一元，即可由①得y=10-x③，把③代入②得2x+（10-x）=16，解得x=6. 筆者接著提出第二個問題：你能把③代入①嗎？學生試驗后發現不能，因為式子會回到原來的模式. 最后，筆者提出了第三個問題：你能求出y的值嗎？學生回答：把x=6代入③得y=4.

教師通過這三個不同層次的問題，讓學生進一步了解利用消元法解二元一次方程組的關鍵之處在于“代入”這一步. 在問題的引導下，學生的探究變得更加有規律和方向. 這樣一來，學生的學習效率自然能夠有所提升，探究也會變得更加簡單.

轉變教學理念，師生共同探究

在傳統的教學模式下，教師一直處于“高高在上”的地位，教師總是主導著整個課堂的進展. 長期處于這種環境之中，學生的主觀能動性以及探究欲望就會受到壓制，這種情況并不利于探究課堂的形成. 因此，教師應當轉變教學理念，讓學生做課堂的主人，與學生一起共同探究，提高探究課堂的效率.

筆者在引導學生探究“不等式的性質”時，在課堂上利用天平的變化，促進學生總結不等式的性質. 首先，筆者在天平的兩端放置了不同重量的砝碼，然后引導學生在天平的兩端加上或者減去同等質量的砝碼. 在學生的操作下，他們發現這樣的操作并不會使天平的方向發生變化，于是我們總結出不等式的第一個基本性質：不等式的兩邊都加上（或減去）同一個整式，不等號的方向不變. 隨后，筆者引導學生對天平進行操作，將天平兩端的砝碼同時乘或者除以同一個正數，經過操作，學生得出天平的方向依然不變的結論，于是我們又總結出了不等式的第二個基本性質：不等式的兩邊都乘（或除以）同一個正數，不等號的方向不變.

在教學行為中，教師要努力轉變以往的觀念，通過對教學理念的轉變，讓師生可以處在一個平等的地位，并在教師和學生的共同合作探究中，讓學生體驗到獲得知識的樂趣以及探究成功的喜悅. 這樣的教學途徑，能促進學生意識到自己的主體作用，做學習的主人，做課堂的主人，做積極的探究者.

利用變式訓練，培養探究思維

在素質教育不斷發展的過程中，培養學生的學習能力已經成為教師的主要教學任務. 要讓初中數學課堂從知識課堂向探究課堂轉變，就必須讓學生意識到探究的重要性. 變式訓練的運用，能夠有效地培養學生的探究思維，最重要的是，它能夠訓練學生舉一反三的能力，幫助學生理解更多不同類型的數學問題本質，真正引導學生以不變的思想與方法挑戰千變萬化的問題，真正達到學以致用的效果.endprint

如二次函數問題：已知二次函數的圖像經過A（-3，0），B（1，0），C（0，-3）三點，求這個二次函數的解析式. 這個問題比較簡單，為了能夠提高學生的探究能力，培養學生的探究思維，筆者對這一問題進行了變式.

變式1？搖 已知二次函數的圖像經過一次函數y=-x-3的圖像與x軸、y軸的交點A，C，且經過點B（1，0），求這個二次函數的解析式.

變式2？搖 已知拋物線經過B（1，0），C（0，-3）兩點，且對稱軸為直線x=-1，求這個拋物線的解析式.

變式3？搖 已知一次函數的圖像經過點（1，0），且y軸上的截距是-1，它與二次函數的圖像交于A（1，m），B（n，4）兩點，又二次函數的對稱軸是直線x=2，求這兩個函數的解析式.

對原有問題進行變式之后，問題變得更具曲折性，需要學生進行深入的思考和探究，并結合之前所學的知識，才能順利解答變式問題. 在做變式訓練的過程中，學生的探究思維得到了有效地開發，而知識與技能的深度和廣度也得到了有效地訓練和變通，學生的學習效能也得到了真正地提升.

給予交流空間，讓探究更自由

很多時候，知識課堂無法向探究課堂轉型的原因是學生缺乏交流的空間，學生在思維與參與的過程中，缺乏足夠的思維空間與時間，這也就意味著學生缺乏探究的自由. 而探究，應當是自由的，學生在一個特定的環境中針對某一個或者多個問題進行探究時，大家應暢所欲言地發表自己對數學知識的理解和看法，在此過程中，學生的思維會得到洗禮，探究能力也會隨之提升. 所以，為了形成探究課堂，教師應當給予學生足夠的交流空間.

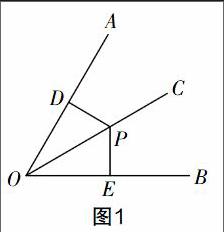
開展“角的平分線性質”教學時，為了能夠讓學生掌握本節課的重點內容，筆者在課堂上給予了學生充分的時間，引導他們對角平分線的性質進行探究和交流. 課堂上，學生按照筆者的提示將一個角（∠AOB）對折，再折出一個直角三角形，展開之后觀察兩次折疊形成的三條折痕，在大家的觀察和討論下，得出了這樣一個結論：已知一個點在一個角的平分線上，則這個點到這個角兩邊的距離相等. 隨后，筆者又引導學生對這一命題用數學方法進行科學、嚴謹地求證. 于是，大家畫出了圖（如圖1），并標出相應字母之后進行證明：因為 PD⊥OA，PE⊥OB （已知），所以∠PDO=∠PEO=90°（垂直的定義）. 在△PDO和△PEO中，因為∠PDO=∠PEO（已知），∠AOC=∠BOC（已知），OP=OP（公共邊），所以△PDO≌△PEO（AAS）. 所以PD=PE（全等三角形的對應邊相等）.

在教師的引導下，給予學生足夠的交流空間，讓學生進行自主探究或合作交流，這種方式能讓學生體會到自己的主體作用，并且可以加深對數學知識的印象. 相信初中生能夠對交流的空間進行合理地運用.

總而言之，將知識課堂轉化為探究課堂，需要的不僅僅是幾個簡單的步驟，而是教師對于教學內容以及學生學情的深入了解，是師生雙方之間的相互配合，是教學理念的改變，是教學方法的完善和強化. 希望以上幾點建議能夠為廣大教師同行起到一定的幫助作用.endprint