鏈條桌邊下落問題的探究

陳 思 李巖松

(1清華大學機械學院汽車工程系，北京 100084； 2清華大學物理系，北京 100084)

“鏈條(軟繩)下落”的習題經常出現在一些高中和大學的物理題目中，用來考察學生對于動量守恒和功能原理的理解和應用。有很多專家和學生對這類習題進行了深入的討論和分析[1-4]。文獻[5]就鏈條中科學問題介紹了國內外進展，而文獻[6]則從教學角度對這一話題進行了梳理。為了能夠在有限的時間之內，得到這類問題的答案(這樣教師“教”和學生“學”都顯得有“信心”)，自然要對問題進行簡化和理想化。鏈條被簡化成“細”“軟繩”和“質量均勻分布”，對限制繩的接觸面簡化成“光滑”。這些簡化在解題中是被默認了。另外一個非常關鍵的默認簡化是繩子始終與光滑接觸面接觸。這個簡化則有待深入分析。

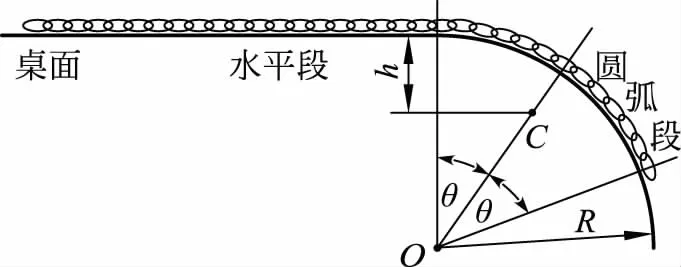
圖1 鏈條下滑示意圖

本文以圖1所示的鏈條沿圓弧形桌邊下落模型論證了鏈條會飛離桌邊的依據，確定了飛離點位置，最后對相關文獻中的有關飛離問題進行了討論。

1 飛離分析

1.1 速度

圖1中，柔軟細鏈條的質量均勻分布；長度為l;線密度為λ;桌邊的圓弧半徑為R。接觸面光滑。假設鏈條一端從桌邊圓弧的起始位置被觸發下滑,初始速度為零。

不失一般性，先假定初始階段鏈條與圓弧段貼合，一直運動到圖1所示的2θ角位置。整個鏈條沿桌面繃緊運動，故各點速率v相同，因此鏈條動能Ek為

圖1中的鏈條圓弧段的重心位于C處，由理論力學得知

因此，圓弧段質心下降高度為

根據機械能守恒，有

即

(1)

1.2 支持力

鏈條內部有張力T，此張力沿鏈條的切線方向，但是會隨鏈條內斷面位置的變化而變化。用s表示鏈條斷面的位置，則鏈條內部張力的矢量形式為T=T(s)τ，其中τ為切向單位矢量。在數學上T=T(s)τ就如同弧坐標中的速度=v(s)τ。類似于從弧坐標的速度到加速度，我們分析dT/ds，有

即

(2)

其中，n為鏈條的法向單位矢量；ρ為鏈條的曲率半徑。

顯然柔軟鏈條與柔弱細繩沒有本質差異。為了便于畫圖顯示，把鏈條畫成橫斷面沿鏈條完全不變的柔軟細繩?？疾旒毨K在桌角圓弧段上的一個微元段ds，見圖2。由式(2)有

(3)

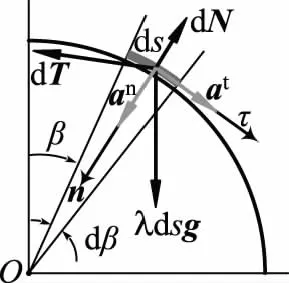
圖2 柔軟細繩下滑示意

沿法向對微元運用牛頓第二定律，有

(4)

即

(5)

式(4)對桌子水平面也是成立的，只不過ρ=∞。此時還有β=0，因此dN=λgds，它不會小于零。這表明鏈條始終與桌子水平面有壓力，因而水平段不可能跳起來。

鏈條不能抗壓，所以張力T總是大于零的；它在鏈條兩端等于零，因為是自由的邊界。如果鏈條足夠長，在水平段有足夠的長度，那么從β=0到β=θ，圓弧段的張力必然單調減小，即式(5)第二項是單調減，第一項對β也是單調減的，而第三項不隨β變化。綜上，dN最小應發生于β=2θ，此處又有T=0，故在鏈條的下落末端有

1.3 飛離

末端飛離的臨界條件為dN=0

即

(6)

引入γ=π/4-θ，式(6)可寫為

(7)

對R/l很小的情形，γ必然很小，此時就有sinγ≈γ;cos2γ≈1，從式(7)可近似解得γ≈πR/l，即下落端到：

2θ=2(π/4-γ)≈π/2-2πR/l

(8)

鏈條末端就會飛離。

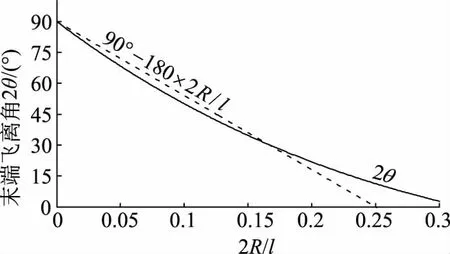
圖 3

對R/l不是很小的情形，式(5)要用數值法求解。利用Matlab的fminsearch求出的結果如圖3所示。

圖3和式(8)表明，只有當R/l→0時，才可能2θ=π/2(=90°)，即鏈條末端在脫離桌面時垂直下落。只要R/l非零，則鏈條末端并不會一直沿圓弧段滑動到垂直才下落，而是在未到垂直之前就會飛離。

R/l=0的情形物理上不可實現，在數學考察R/l→0，那么式(5)中第三項將趨近于負無窮(ρ=R),更無法保證dN≥0，也就是更不可能保證繩與桌角貼合。

綜上所述，圖1所示的問題中：鏈條脫離桌面后不可能保持垂直；下落的端點在達到垂直之前就應該飛離。

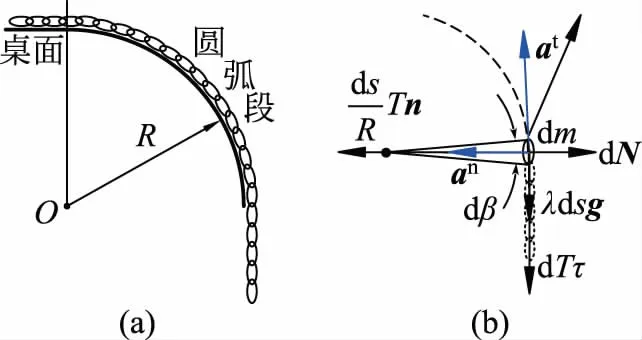
圖 4(a) 模型; (b) 最后一環分析

2 討論

(1) 文獻[1]中例2的鏈條已經懸垂于桌面下，從靜止再釋放。這也不能保證鏈條與桌角的貼合。論證如下。

式(5)也適用于鏈條末端已垂于桌面之下。對桌角半徑R/l→0的情形，第三項必然是趨于負無窮，無法保證貼合條件dN≥0。

對R/l有限的情形，采用反證法，即先假定鏈條與桌角一直貼合。我們來分析鏈條最后一環，它在離開桌面之前的受力分析如圖4(b)所示，其中鏈條張力按照式(3)分解了。由于處于鏈條末端，所以進一步有T=0，這樣沿水平方向就有

-dN=λdsg×an=λdsg×v2/R>0

即dN<0。這表明假設錯誤。真實情形應該是在脫離之前，某段鏈條會飛離桌面。

(2)文獻[2]分析了圖5所示的軟繩沿桌面小孔下落的問題。該文作者分別采用了動量定理和動能定理兩種方法，發現二者結果不一致。實際上軟繩自小孔邊緣下落，與圖1的模型類似，軟繩會飛離小孔的倒角圓弧。如果小孔很小，那么飛離的軟繩必然與小孔的內壁碰撞，因而落下段不能保持直線。如果小孔小到在孔內段，繩子近似保持直線，那么繩子到小孔的下方也不能保持直線。因此，文獻[2]計算落下段的動能和動量的方式值得深入分析。

圖5

(3) 文[6]討論了鏈條在滑輪上下落的問題，研究了鏈條從滑輪上飛離的條件，但是由于微元段沒有考慮重力，所以飛離條件應按式(5)重新分析。

如果張力在圖1弧形段的大小可以近似相等(在1.2節的分析中沒有承認它近似相等)，那么隨弧上位置變化的是β。當β=90°時，式(5)右邊最小，它對應最容易飛離的位置(而不是文獻[6]中的β=0)。在此位置，飛離條件為

T=λv2/R

如果T沿弧形段的大小變化很明顯，則確定飛離位置和飛離條件還是很麻煩的。

3 結語

從上文分析我們可以看出，對于“鏈條桌邊下落模型”的分析是較為復雜的，很難在沒有計算機輔助的情況下進行求解、分析。為了出題方便而簡化的條件不僅不會幫助學生掌握知識，還會錯誤地引導學生。因此高中和大學的考試中，應當

避免利用該模型對“動量守恒”“功能原理”知識點進行考察。本文對于“飛離”這一過程的討論還不全面，應當繼續求解飛離的水平方向速度，可以嘗試通過對“鏈條受力”的積分計算，求鏈條水平方向受到桌子的作用力，進而利用“水平方向動量定理”求出飛離的速度。

[1] 楊元平，高翔. 對機械能守恒定律“五性”的理解[J]. 物理教師，2003(10): 4-6. YANG Yuanping, GAO Xiang. Understanding conservation law of mechanical energy from 5 aspects[J]. Physics Teachers， 2003(10): 4-6. (in Chinese)

[2] 吳海娜, 劉順, 公衛江，等. 用微元法巧解軟繩下落過程的能量損失[J].物理與工程，2016,26(1):72-75. WU Haina, SHUN Liu, GONG Weijiang, et al. The energy loss of the falling process of soft rope using microelement method[J]. Physics and Engineering. 2016, 26(1): 72-75.

(in Chinese)

[3] 劉斌. 充分發揮習題的作用培養學生獨立解決問題的能力[J]． 物理與工程， 2014， 24(4): 11-19． LIU Bin. To give full play to the role of exercises to cultivate students’ ability to solve problems independently[J]． Physics and Engineering, 2014， 24(4): 11-19． (in Chinese)

[4] 鄭國安.下降鏈條的能量損失[J].物理教師,2005,26(5):41-42. ZHENG Guoan. The energy loss of the descending chain[J]. Physics Teachers, 2005, 26(5): 41-42. (in Chinese)

[5] 于同旭，張文彬，許騰，等. 鏈條下落運動問題淺析[J].自然雜志，2015,37(1):53-60. YU Tongxu， ZHANG Wenbin， XU Teng et al. Discussion of the chain falling movement[J]. Chinese Journal of Nature, 2015, 37(1): 53-60. (in Chinese)

[6] 路峻嶺，秦聯華，任乃敬. 關于柔軟細繩運動問題中加速度奇點的討論[J].大學物理,2016,35(12):7-12. LU Junling， QIN Lianhua， REN Naijing. Discussion on the speed singularity of soft string movement[J]. College Physics, 2016, 35(12): 7-12. (in Chinese)