例析高考試題中平面向量的四大運算策略及教學反思

田秀權

平面向量作為代數和幾何的紐帶，素有“和平面幾何聯姻，與代數牽手，與解析幾何交匯”之美稱，在近幾年高考試題中，平面向量題已然成為命題的重點和熱點，在客觀題中大多出現在壓軸題位置，向量題的特點是：知識交匯自然，解法靈活多樣；但萬變不離其宗，緊扣“數”和“形”的本質屬性，思考和解決問題，本文以近兩年高考試題為例，分析、提煉平面向量的四大處理策略，以指明解題方向，優化解題過程，提高解題效率，并反思教學.

1代數化策略

1.1坐標運算策略

所謂坐標運算策略，是指解決平面向量問題時，把有關已知條件和所求結論，在直角坐標系中恰當地表示出來，這樣就將向量運算完全代數化，可將幾何問題轉化為學生熟悉的有明確關系的數量運算，從而減少問題的思維量，降低問題的難度，

例1 （2017年高考全國卷Ⅱ.理12）已知△ABC是邊長為2的等邊三角形，P是平面ABC內一點，則PA·（PB+PC）的最小值是（

）

A.-2

B.-3/2 C.-4/3 D.-l

解以BC為x軸，BC的垂直平分線AD為y軸，D為坐標原點建立直角坐標系（如圖1），

則B（-l，0），c（1，0），A（O，√3）.

設P（x，y），所以PA：（-x，√3-y），

PB=（-1-x，-y），PC=（1-x，-y），

評注本題作為選擇題的壓軸題，對學生的能力要求比較高，如果方法選擇不恰當，處理起來較為困難，考慮到圖形的對稱性，利用坐標運算策略，具體明確地表示出各個向量，從而問題得以快速解決，也使我們體會到了坐標運算策略的筒捷和明快.

1.2數量積運算策略

所謂數量積運算策略，是指解決平面向量問題時，把題目中的向量等式主動施加恰當的數量積運算，這樣把向量運算完全代數化，這是處理棘手向量等式問題的重要思路，數量積運算策略體現了構造思想、轉化和化歸數學思想.

評注這是一道中等偏上難度的題，考查了兩角和差公式、向量數量積兩個C級考點知識的交匯，彰顯了重點知識重點考查的命題理念，利用數量積運算策略，把問題完全代數化，構造了關于目標參數的方程組，思路清晰明了.

2幾何化策略

2.1線性運算策略

所謂線性運算策略，是指解決平面向量問題時，利用平面向量的加減運算、數乘運算以及平面向量基本定理來解決問題，求解時通常選擇兩個信息量（模、角、位置關系）大、關聯性強的不共線的向量作為基底，然后把其他向量用基底表示出來.

2.2圖形運算策略

所謂圖形運算策略，是指解決平面向量問題時，作出題目中所涉對象的幾何圖形，借助圖形思考問題（往往結合平面幾何知識、幾何意義等等），借助圖形解決問題，圖形運算策略體現了數形結合的數學思想，是平面向量的一個本質特性.

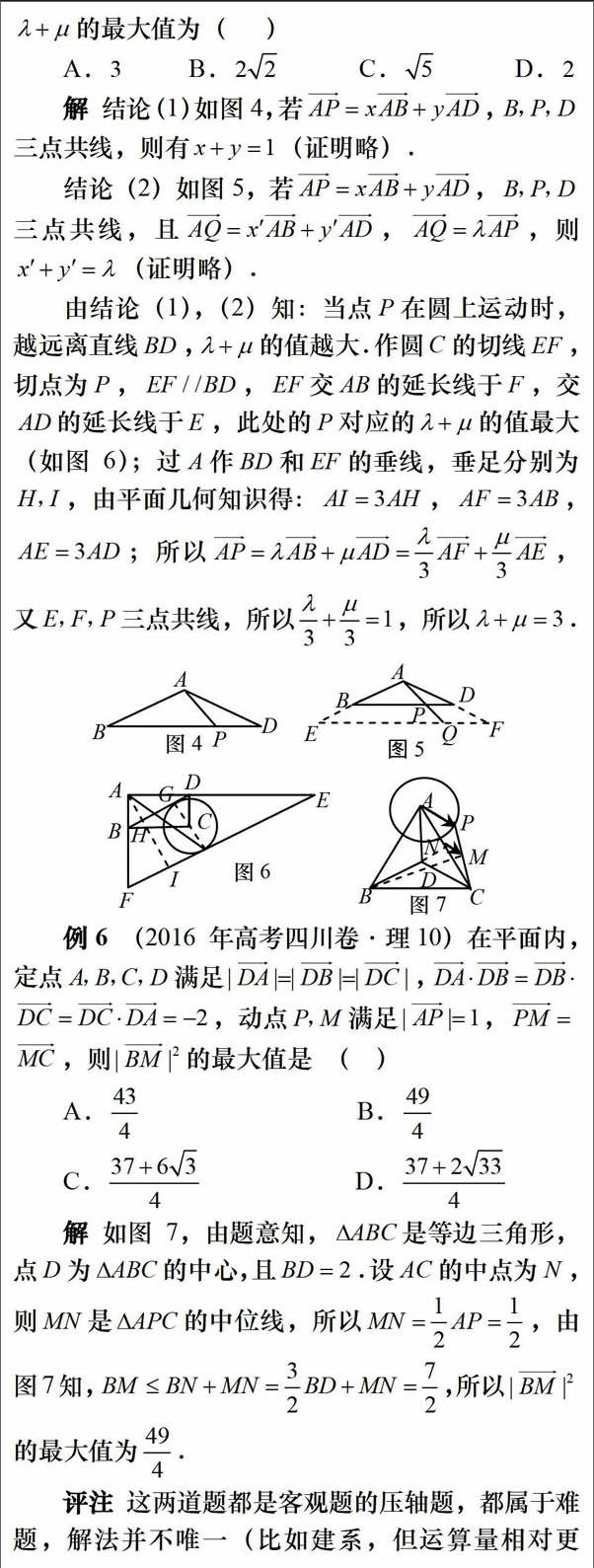
評注這兩道題都是客觀題的壓軸題，都屬于難題，解法并不唯一（比如建系，但運算量相對更大）.如果利用好圖形運算策略，讓問題更形象直觀、解法更簡潔明了，思維更活躍靈動，圖形運算策略體現了幾何直觀的數學核心素養.

3教學啟示

3.1本質探究是根本

數學問題解決的過程，是從已知向未知尋求聯系的過程，并努力去尋找條件和結論之間的數學本質，作為位置偏后的填空題，往往涉及的知識點是多元的、交匯的，研究對象的關系是錯綜復雜的，如何能讓學生有序思維，理清基礎知識，精準的找到問題的切入口？這就要求我們平時的教學要注重知識的生成、發展過程，重視對知識本質屬性及問題本質的探究，比如：平面向量的概念是什么？有怎樣的本質屬性？了解了這樣的問題，解題的思路就會更加自然流暢；正所謂“問渠那得清如許，為有源頭活水來”，數學問題本質的挖掘正是解題思路的“源頭活水”.

3.2方法提煉要精細

平時的解題教學應追求通性通法，比如多元問題需消元、高次問題要降次，常用帶入、換元、待定系數等方法，學習、應試是個不斷積累的過程，有必要積累一些處理問題的基本方法，然而方法的提煉僅僅停留在淺層次的“方法名稱的記憶”肯定是不行的，方法的提煉應該要更加精細化，讓學生經歷思考、分析、對比、選擇的思維過程，提煉出方法及方法的適用性，譬如：本文中總結的解決平面向量題的四大解題策略，怎樣的題型特點適合用坐標運算策略？怎樣的題型特點適合用線性運算策略？這四種策略是否有一定的關聯性？

3.3能力訓練重反思

“選拔性”是高考試卷的重要指標之一，這也決定了以能力立意的命題理念，學生的解題能力哪里來？怎么來？教師的講解和學生的解題訓練固然重要，但能力的形成和提升更離不開學生的自我感悟和自我反思，荷蘭著名數學教育家弗賴登塔爾就曾指出：“反思是數學思維活動的核心和動力”，教師經常有著這樣的困惑或抱怨：“這樣的題講過好幾遍了，稍微改變一下，學生怎么又不會啦？”問題的關鍵就在于學生“悟得少”，其實，學生解題能力的提高是在學習過程中通過不斷地分析問題、轉化問題，通過不斷地聽懂、反思、對比、感悟、內化、遷移和運用達成的.endprint