“低起點、高觀點、高目標(biāo)”在數(shù)學(xué)實驗活動課堂上的體現(xiàn)

徐偉東

摘?要：本文通過一堂數(shù)學(xué)實驗活動課，運用啟發(fā)式、探究式、討論式的教學(xué)方法，激發(fā)學(xué)生的好奇心，讓學(xué)生參與課堂教學(xué)，為學(xué)生營造了獨立思考、自主探索、勇于創(chuàng)新的良好環(huán)境，幫助學(xué)生學(xué)會學(xué)習(xí)，提升了學(xué)生的解題能力。

關(guān)鍵詞：數(shù)學(xué)實驗;低起點;高觀點;高目標(biāo)

中圖分類號：G633.6文獻標(biāo)識碼：A ????文章編號：1992-7711（2018）24-099-2

“低起點”，是指從最基本的知識起，或從學(xué)生最感興趣的生活經(jīng)驗出發(fā)，設(shè)置懸念，創(chuàng)設(shè)一種教學(xué)的情景，以激發(fā)學(xué)生的思維活動。

“高觀點”，是指一切有利于發(fā)展初中生數(shù)學(xué)核心素養(yǎng)的觀點。本文中的高觀點有兩個：教師對教材理解高觀點，課堂教學(xué)方式追求的高觀點。只有老師能居高臨下地把握教材，才能真正把準(zhǔn)本學(xué)科教學(xué)脈搏，學(xué)生才能在高觀點的指導(dǎo)下成為課堂的主人，運用高觀點去分析問題、認識問題。

“高目標(biāo)”應(yīng)該是學(xué)科教學(xué)的終極目標(biāo)，既要高質(zhì)量的完成教學(xué)目標(biāo)，又要挖掘和開發(fā)學(xué)生的潛能，讓學(xué)生在充分動腦、動手的課堂中提高學(xué)習(xí)能力、實踐能力、創(chuàng)新能力，從成功中發(fā)現(xiàn)自我。教學(xué)的“低起點、高觀點、高目標(biāo)”要落實在日常的課堂教學(xué)中，做到潤物細無聲。下面以筆者開設(shè)的蘇科版七年級數(shù)學(xué)實驗活動課《數(shù)值轉(zhuǎn)換機》為例，來分析課堂教學(xué)中如何體現(xiàn)“低起點、高觀點、高目標(biāo)”。

課堂首先從“試用一個你喜歡的x值，求代數(shù)式5（x+1）-2的值。”引入，這是一個低起點的引入，學(xué)生對求代數(shù)式的值都能理解，也能熟練掌握，用一個學(xué)生喜歡的x的值，更激發(fā)了學(xué)生學(xué)習(xí)的興趣。接著從輸入x的值開始通過數(shù)值轉(zhuǎn)換機寫出輸出結(jié)果（如圖），

這個過程實質(zhì)就是構(gòu)造一個代數(shù)式（即構(gòu)造一個簡單的一次函數(shù)），再接著從代數(shù)式1/2（x+3）-5寫出轉(zhuǎn)換程序，這個過程就是還原函數(shù)的構(gòu)建過程。

通過學(xué)生的討論來熟練掌握程序轉(zhuǎn)換機的原理，每個類型通過三個式子的練習(xí)讓學(xué)生熟練掌握數(shù)值轉(zhuǎn)換機的方法（即一次函數(shù)的構(gòu)建），逆向操作，還原了一次函數(shù)的生成過程，學(xué)生心情愉悅，他們從討論中獲得了知識，在探究中得到了新的知識。其實學(xué)生發(fā)現(xiàn)的，就是八年級馬上就要學(xué)習(xí)的一次函數(shù)的相關(guān)知識。

高觀點：把課堂交給學(xué)生，讓學(xué)生在課堂上學(xué)，通過學(xué)生動腦、動手，再由學(xué)生交流、講解得出結(jié)論，也充分體現(xiàn)了學(xué)生的主體地位。

當(dāng)然要實現(xiàn)高目標(biāo)對學(xué)生來說還是有一定難度的，課堂上接著再問：生活中有沒有類似的數(shù)值轉(zhuǎn)換機呢？

給出生活中的實例：

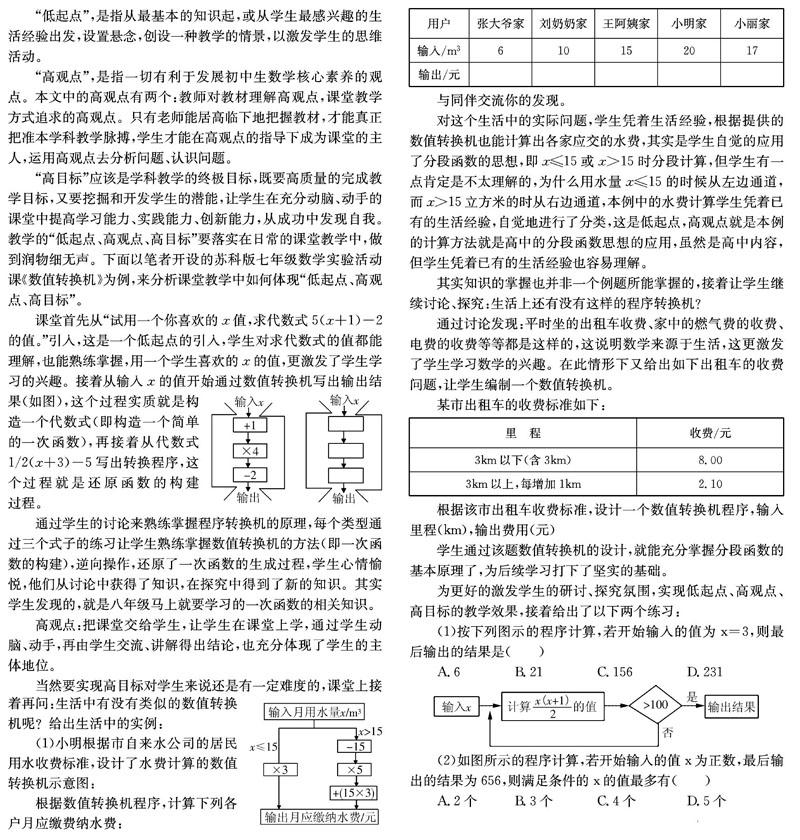
（1）小明根據(jù)市自來水公司的居民用水收費標(biāo)準(zhǔn)，設(shè)計了水費計算的數(shù)值轉(zhuǎn)換機示意圖：

根據(jù)數(shù)值轉(zhuǎn)換機程序，計算下列各戶月應(yīng)繳費納水費：

與同伴交流你的發(fā)現(xiàn)。

對這個生活中的實際問題，學(xué)生憑著生活經(jīng)驗，根據(jù)提供的數(shù)值轉(zhuǎn)換機也能計算出各家應(yīng)交的水費，其實是學(xué)生自覺的應(yīng)用了分段函數(shù)的思想，即x≤15或x>15時分段計算，但學(xué)生有一點肯定是不太理解的，為什么用水量x≤15的時候從左邊通道，而x>15立方米的時從右邊通道，本例中的水費計算學(xué)生憑著已有的生活經(jīng)驗，自覺地進行了分類，這是低起點，高觀點就是本例的計算方法就是高中的分段函數(shù)思想的應(yīng)用，雖然是高中內(nèi)容，但學(xué)生憑著已有的生活經(jīng)驗也容易理解。

其實知識的掌握也并非一個例題所能掌握的，接著讓學(xué)生繼續(xù)討論、探究：生活上還有沒有這樣的程序轉(zhuǎn)換機？

通過討論發(fā)現(xiàn)：平時坐的出租車收費、家中的燃氣費的收費、電費的收費等等都是這樣的，這說明數(shù)學(xué)來源于生活，這更激發(fā)了學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣。在此情形下又給出如下出租車的收費問題，讓學(xué)生編制一個數(shù)值轉(zhuǎn)換機。

某市出租車的收費標(biāo)準(zhǔn)如下：

根據(jù)該市出租車收費標(biāo)準(zhǔn)，設(shè)計一個數(shù)值轉(zhuǎn)換機程序，輸入里程（km），輸出費用（元）

學(xué)生通過該題數(shù)值轉(zhuǎn)換機的設(shè)計，就能充分掌握分段函數(shù)的基本原理了，為后續(xù)學(xué)習(xí)打下了堅實的基礎(chǔ)。

為更好的激發(fā)學(xué)生的研討、探究氛圍，實現(xiàn)低起點、高觀點、高目標(biāo)的教學(xué)效果，接著給出了以下兩個練習(xí)：

（1）按下列圖示的程序計算，若開始輸入的值為x=3，則最后輸出的結(jié)果是（ ）

A.6B.21C.156D.231

（2）如圖所示的程序計算，若開始輸入的值x為正數(shù)，最后輸出的結(jié)果為656，則滿足條件的x的值最多有（ ）

A.2個B.3個?C.4個D.5個

練習(xí)（1）表面上通過程序計算，求代數(shù)式的值，但實質(zhì)是要通過條件判斷，反復(fù)輸入，直至有符合條件的結(jié)果出來，才能得到最后結(jié)果231;而練習(xí)（2）則是從輸出結(jié)果出發(fā)，不斷反推，得到一個個x的值，即：131、26、5、4/5，通過這樣一個討論、探究的過程，學(xué)生實質(zhì)上就體會著根據(jù)自變量求函數(shù)值的過程，根據(jù)給出的函數(shù)值，求自變量的過程，既訓(xùn)練了學(xué)生的思維，又為后續(xù)學(xué)習(xí)函數(shù)的相關(guān)知識作了良好的鋪墊。

高目標(biāo)、高觀點：發(fā)現(xiàn)生活中的數(shù)值轉(zhuǎn)換機，要的是學(xué)生的數(shù)學(xué)素養(yǎng)、科學(xué)態(tài)度，讓學(xué)生深刻意識到數(shù)學(xué)是一門以生活為基礎(chǔ)的學(xué)科，數(shù)學(xué)來源于生活，也來源于數(shù)學(xué)實驗活動，科學(xué)嚴謹?shù)膶嶒瀾B(tài)度是很多重要發(fā)現(xiàn)的前提。

該節(jié)數(shù)學(xué)實驗活動課，讓學(xué)生通過已有的生活經(jīng)驗和已有的數(shù)學(xué)知識，來解決生活中的實際問題，不但培養(yǎng)了學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，而且使學(xué)生在活動過程中表現(xiàn)出學(xué)會合作、學(xué)會討論、勇于發(fā)現(xiàn)的探索精神，使他們在課堂上嘗試到了成功的喜悅。

以上事例說明，低起點是實現(xiàn)高觀點、高目標(biāo)的基礎(chǔ);高觀點是實現(xiàn)高目標(biāo)的主導(dǎo);高目標(biāo)是低起點、高觀點的必然結(jié)果。三者三位一體、相輔相成、和諧統(tǒng)一。