類別數據擬合優度檢驗功效模擬

劉遵雄

（華東交通大學 信息工程學院，南昌330013）

0 引言

類別數據廣泛應用于教育、心理和經濟等社會生活方面，如社會調查和心里測驗等領域中使用的態度量表（Likert型數據）[1]。當需要考慮收集的一組類別數據符合何種分布問題時，一般采用擬合優度檢驗方法。類別數據擬合優度檢驗很多，有卡方（χ2）檢驗和經驗分布類檢驗（如Kolmogorov-Smirnov檢驗）等，其中卡方檢驗是離散類別數據分布檢驗的首選，而經驗分布類檢驗適用于連續分布數據的檢驗。

擬合優度檢驗的功效（power）是指備擇假設H1為真時檢驗方法拒絕零假設H0的能力，定義1-β，其中為犯第二類錯誤的概率。類別數據擬合優度檢驗功效無法進行解析表示，一般通過蒙特卡羅模擬來獲得功效近似值[2，3]。

本文在對類別數據擬合優度檢驗方法進行研究的基礎上，使用卡方、Mann-Whitney和Kolmogorov-Smirnov檢驗方法進行10單位（實驗結果種類）的均勻零假設分布對不同備擇分布數據的擬合優度檢驗，計算檢驗方法的功效，并給以分析說明。

1 檢驗統計量及實驗設置

1.1 類別數據擬合優度檢驗統計量

卡方（χ2）檢驗法是最重要而典型的類別數據擬合優度檢驗方法，其對觀察頻數及期望頻數間的差異進行比較，并利用差異的單調函數來衡量給定分布擬合數據的效果。卡方檢驗統計量表示為：

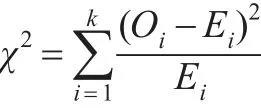
其中k是實驗結果種類數，Oi和Ei分別是第i種實驗結果的觀察和期望頻數（在以下統計量中出現時意義相同）。

Kolmogorov-Smirnov（KS）檢驗[4]比較樣本的經驗分布函數（empirical cumulative distribution function,ecdf）和零假設H0情況下的理論經驗分布函數（cumulative distribution function,cdf）值差異的最大值，其中cdf可以看作服從[0，1]的均勻分布（U(0，1)）的隨機變量。對于離散類別數據，Kolmogorov-Smirnov檢驗統計量S：

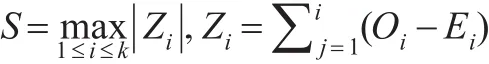
Mann-Whitney（MW）檢驗[5]假設兩樣本分別來自除總體均值差別外完全相同的兩個總體，目的是檢驗這兩個總體的均值是否有顯著的差別。假設服從零假設分布和備擇分布的兩樣本數各自為n0和n1，將這兩組樣本混合后進行秩排序，得到兩組樣本的秩和R、R，計算U統計量：

1.2 檢驗功效模擬實驗設置

使用蒙特卡洛模擬方法求得各擬合優度檢驗的功效，選定零假設分布為10種實驗結果的均勻分布，備擇分布分別為遞降分布、三角形分布和扁平分布（其10種實驗結果的發生概率見表1）。模擬實驗中的樣本大小分別為10，20，30，50，100和200（即對應零均勻分布下每種實驗結果的觀察數分別為1，2，3，5，10和20）。這些檢驗的功效是由10000次模擬實驗得到的，每次模擬將產生樣本數不同的零分布和備擇分布數據，檢驗的置信水平設為0.05。

表1 檢驗功效模擬實驗零假設分布及備擇分布

作用于類別數據的這些統計量的模擬分布是離散的，為了獲得置信水平0.05下的檢驗功效，這里采用線性插值方法[5]。假設α為檢驗的置信水平，α1為小于α的一個置信水平，α2為大于α的一個置信水平，則α置信水平下檢驗的功效計算為：

2 實驗結果分析

2.1 遞降備擇分布

當備擇分布為遞降分布時，在不同樣本情況下，通過蒙特卡洛模擬求得三種擬合度檢驗χ2、KS和MW檢驗的功效（如圖1），可見MW檢驗功效最好，KS檢驗功效次之，χ2檢驗功效最差。在樣本大小至少是每個實驗結果發生次數10以上時，三者的功效基本相當（在0.87以上）。當樣本大小為200時，三者的功效都幾乎為1。

圖1 均勻零分布遞降備擇分布下三種檢驗的功效

3.2 三角形備擇分布

當備擇分布為三角形分布時，在不同樣本情況下，三種擬合度檢驗（χ2、KS和MW檢驗）的功效如圖2。從中可以看出，當類別數據的分布為三角形時，判別該數據是三角形分布還是均勻分布，三種檢驗效果都不很好（即檢驗功效低）；同比，χ2檢驗功效較好，特別是樣本大小為200時，χ2檢驗功效趨近1（為0.9745），KS檢驗的功效等于0.579。

2.3 扁平備擇分布

在扁平備擇分布情況下，三種擬合度檢驗χ2、KS和MW檢驗對于不同樣本大小的功效如圖3。同比三角形備擇分布，三種檢驗的功效更低。使用這三種檢驗方法檢驗扁平分布數據時，不能很好地將扁平分布數據與均勻分布數據分開。在此條件下χ2檢驗的功效稍好

圖2 均勻零分布三角形備擇分布下三種檢驗的功效

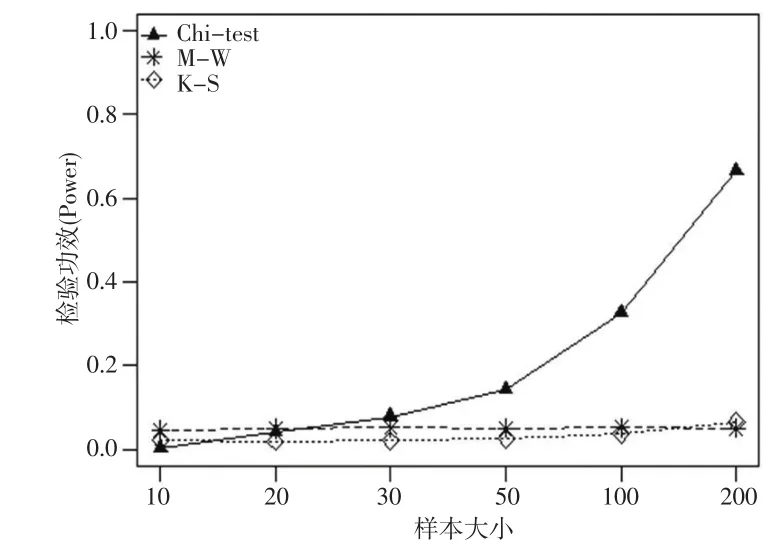
圖3 均勻零分布三角形備擇分布下三種檢驗的功效

當樣本大小為200時，χ2檢驗的功效為0.664。而不管樣本大小如何，KS和MW兩檢驗的功效都很低。

3 結論

使用三種方法進行類別數據擬合優度檢驗，通過蒙特卡洛實驗獲得檢驗功效近似值，結果顯示沒有任何一種擬合優度檢驗方法適合任何情況下的數據擬合檢驗，也就是說要針對具體問題選擇適當的擬合優度檢驗方法。在零假設均勻分布，遞減、三角形和扁平備擇分布情況下，三種擬合優度檢驗（χ2、KS和MW檢驗）中，χ2檢驗是適應性較強的類別數據擬合優度檢驗方法。同時本文將三種方法的檢驗功效評級列于表2，為應用人員選擇擬合優度檢驗方法提供參考。

表2 擬合優度檢驗功效評級