基于經濟增長模型的中國資本存量非線性估計

張益明，趙永亮

（鹽城工學院 經濟管理學院，江蘇 鹽城 224005）

0 引言

資本存量作為一個非常重要的宏觀經濟變量，對于研究經濟增長問題至關重要。長期以來，在官方數據缺失的背景下，資本存量的推算成為研究國內宏觀經濟的重要話題。國內外對其的研究中，大部分文獻主要采用永續盤存法，也有部分文獻采用資本產出比法估算。本文采用經典的經濟增長模型導出計量模型，對資本存量進行非線性估算，而非以永續盤存法為核心。這樣處理可以避開使用爭議較大的歷史數據，以及歷史年份中如何選取折舊率、設定資本產出比等問題。并且，上述好處隨著時間的推移，可得數據的增加，將得到更充分的體現。而采用美國的資本存量數據進行的檢驗表明，本文提出的估計方法能夠獲得較為準確的結果。

1 資本存量估計方法的比較

1.1 基于永續盤存法的資本存量估計

永續盤存法是國內外文獻采用的資本存量估計的主要方法。該方法基于一個直觀的思想，即某時期的資本存量等于本期的投資加上折舊后的上期資本存量。

首先，是基期資本存量的處理。現有文獻對于基期時間一般選擇1952年[1-3]，或1978年[4]。在基期資本存量的估計方法上，采用得最多的是資本產出比法[5]和資本增長率法[2]。

其次，折舊率的處理。早期研究中對于折舊處理形成兩類觀點，一類以張軍和章元[1]為代表，認為可以通過數據選擇回避折舊問題。另一類觀點認為，折舊率必須考慮，但如何選擇無法達成一致。常見的做法是選擇5%的折舊率。再根據殘值率進行推算[6]。此外，現有文獻還嘗試使用可變折舊率進行資本存量估計[3,4]。不可否認，上述處理方法各具特色。從經濟實際發展過程來看，折舊率應該是可變的，但是變化過程無法直接觀察，因此如何處理仍然值得深入探討。本文采用李賓[7]的建議，利用官方折舊數據而避開折舊率的選擇或計算。

再次，投資流量數據。現有研究采用的投資流量數據的選擇包括四類，即固定資本形成總額、新增固定資產、全社會固定資產投資、調整了的全社會固定資產投資。其中固定資本形成總額在研究中使用最多，也被認為最合理。但李賓[7]認為，采用固定資本形成總額僅僅是稍優于全社會固定資產投資。

最后，價格指數選擇。在數據可獲得的情況下，現有文獻一般選擇固定資產投資價格指數平減當期的投資，這被認為是最好的做法。但是正如李賓[7]指出的，我國官方統計資料中最早只能獲取從1991年以來的這一指標，因此涉及到之前年份時就存在數據缺失問題。對此，一般可以通過擬合或尋找替代性的指標來解決。另外，還有一些研究直接借鑒了其他文獻計算的價格指數[4]。

1.2 基于投入產出表的資本存量估計

我國每5年公布一次投入產出表，因此可通過折舊率、折舊額反推資本存量[8]。該方法假設研究的時間窗口存在不變的折舊率，再通過投入產出表公布的折舊額，以及各期的投資流量和價格指數推算各期折舊率，進而得到資本存量。

1.3 上述方法與本文的差異

上述方法一般都是在永續盤存法的基礎上展開的，部分文獻在估計中運用了計量的方法，但是主要用于獲取估計過程中的一些變量。同時不少文獻對于估計的結果采用C-D函數進行了檢驗[7]。這些工作對本文頗多啟發，與本文的工作有一定關聯，但是并不相同。本文對資本存量的估計主要通過對經濟增長模型的變換，得到可計量的模型，根據模型形式分別采用高斯牛頓法迭代法和直接搜索的方法進行資本存量估計。

2 資本存量的高斯牛頓法估計模型

本文從索洛模型出發，假設總產出決定于現有的資本存量與勞動力人數，即：

假設規模報酬不變，則α+β=1，式（1）兩邊取對數有：

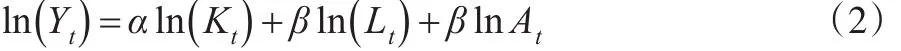
2.1 不考慮平穩性問題

式（2）由于基期資本存量無法獲取難以進行直接估計，但是若不考慮數據平穩性問題，則可以進行轉換后進行估計。比如可以假設基期的資本存量為K0，各期凈投資為It，則式（2）可以寫成：

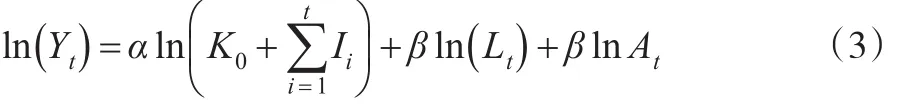
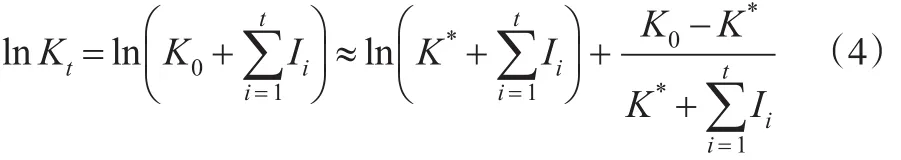
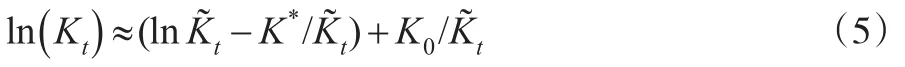
式（5）代入式（3）得到：

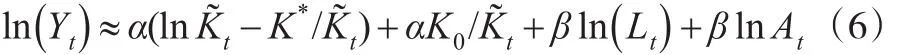
由式（6）出發，假設A為常數，則可以建立模型：

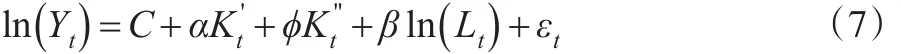
對模型（7）取初始，估計得到α和φ的估計值后，可根據α和φ的關系得到基期的資本存量K0新的估計值，再代入模型進行第二次估計，反復迭代，直到K0的估計值收斂。然而，由于時間序列的平穩性問題，上述方法需要在對數據進行處理后使用，而這也意味著估計的模型形式隨之變化。并且，通過對數據的單位根檢驗，可以發現中國的ln(Yt)為2階單整，而ln(Lt)則為1階單整。這和美國情況不同，美國的GDP以及人均GDP都為1階單整。因此無法進行協整，而必須對原模型進行差分變換。

2.2 考慮平穩性問題

ln(Yt)與其他變量的單整階數不一致，對此建立差分模型進行估計。ln(Yt)單整階數之所以較高主要是因為滿足建模要求的時間期數不夠，只有22期。實際檢驗1952—2015年的數據，發現為1階單整。而對于本文來說，進行兩次差分處理后雖然數據實現了平穩，但是也丟失了很多信息。并且，對于美國的數據而言，因為都是一階單整，因此對數據進行兩次差分建模也不合適。因此，下面在推導了兩次差分后的回歸模型后，也提供了一次差分的回歸模型形式，并在實證中對兩個模型都進行了估計。

假設A為常數，對式（2）進行兩次差分轉換為：

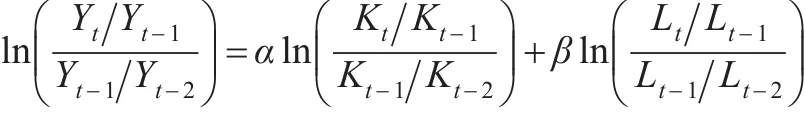
以yt、kt、lt分別表示總產出、固定資本、勞動力t時期的增長率，則有：

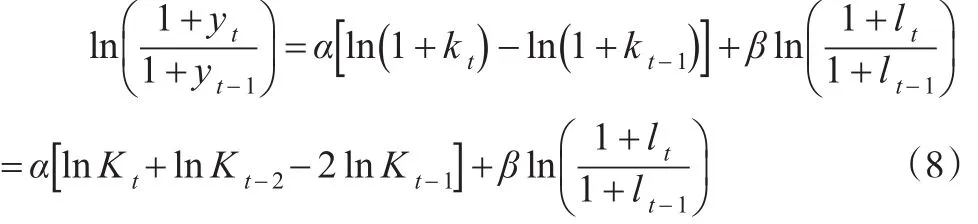
將式（4）代入式（8）得到：

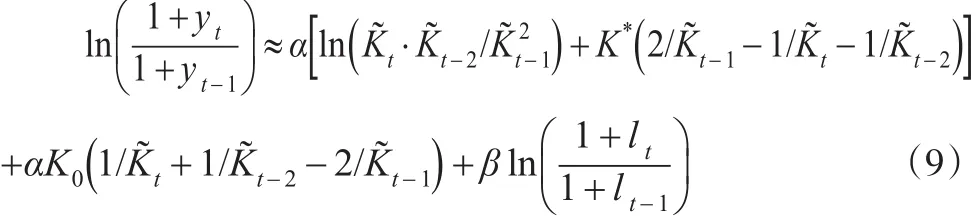
式（9）經過兩次差分，解決了數據的平穩性問題。實際建立模型時，為了控制其他未納入變量的影響，還加入被解釋變量的一階滯后項，得到：

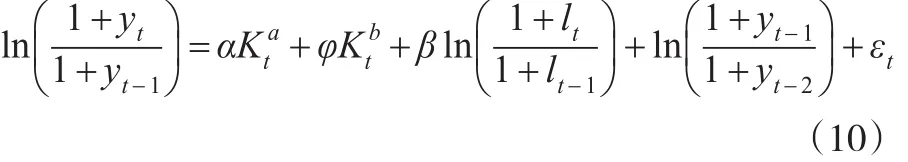
其中：

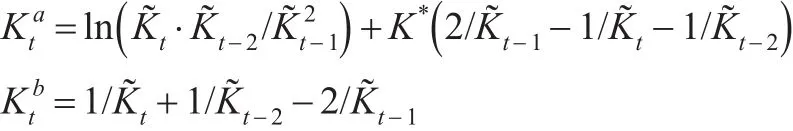
同時，考慮差分導致的信息丟失問題，另外采用一階差分得到的回歸模型：

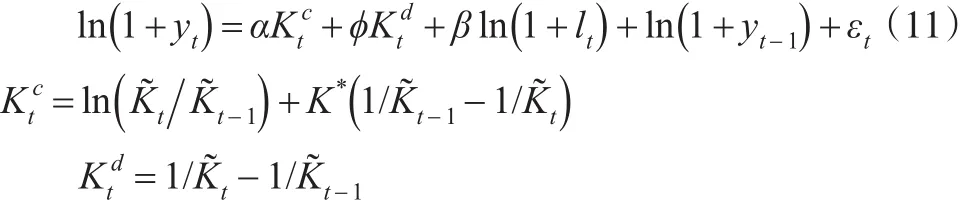
對于模型（10）和模型（11），在取K0的初始值K*后，計算出各期的以及模型中的，進行估計得到α和φ的估計值然后，根據式（9）可知因此以作為下一次迭代時K0的取值。重復上述過程，直至K0收斂。另外，在估計美國資本存量時，本文嘗試在模型（11）中加入了虛擬Badyear的差分項，以反映一些年份實際GDP下降的情況，但對估計結果沒有影響。Badyear在當年GDP小于上一年時取1，否則為0。對于中國1993—2015年間，未發生該情況，因此對中國資本存量的估計未加入該變量。

3 資本存量的直接搜索法估計模型

上文提出的估計方法沿用一個假設，即規模報酬不變。這對于建模而言無疑很方便，但是對于模型估計而言則可能帶來一些問題，比如某些年份中因為一些外生或內生的沖擊導致經濟受到影響時，GDP與資本總量及勞動力的數據可能不匹配，從而對模型估計造成干擾。另外，實際估計過程中，由于計算過程較為復雜，迭代過程可能也會產生一些意想不到的變化，比如得到負的資本存量，使得無法取對數而中止迭代過程。對此，本文由增長模型中人均生產總量與人均資本的關系提出直接搜索法估計模型。

由式（1）可以得到：

假設A為常數1，則兩邊取對數有：

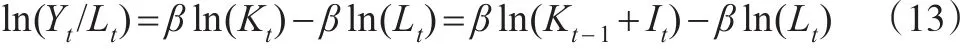
注意到式（13）右邊兩項的系數都是β，但是一正一負。另外，為了反映經濟增長過程中的意外負面沖擊，以及其他因素的影響。同樣還在模型（13）的基礎上加入了對數人均產出的滯后項以盡量控制其他未納入模型的因素。而對于美國資本存量的估計還加入了虛擬變量badyear。在此基礎上，差分后可以建立模型：

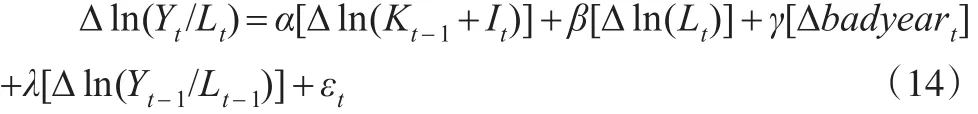
式（14）中Kt未知，可以選擇不同的初始K0，根據模型（4）計算出Kt代入模型（14）進行回歸。當K0選擇合適時，模型（14）的回歸系數α和β符號應當相反，但是絕對值接近。

除此以外，不少測算資本存量的文獻中假設資本產出比為常數，由GDP推測資本存量。而美國的數據也顯示，1950—2014年間，資本產出比居于2.52～3.46之間，大部分年份在3.16上下。若假設該指標確實比較穩定，則模型（12）可以寫成：

假設A為常數，可以推得：

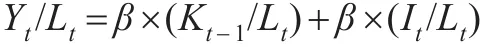
同樣，在上式中加入badyear和人均產出的滯后項，再差分得到模型：

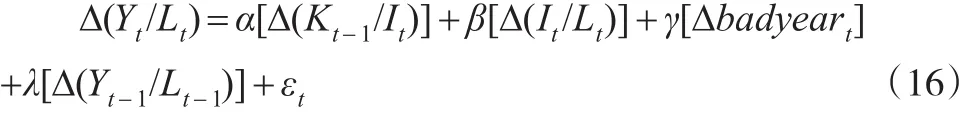
而在對中國資本存量估計時，則沒有badyear的差分項。同樣，當K0選擇合適時，模型（16）的回歸系數α和β符號應當一致，大小接近。而對于K0的選取可以采用直接搜索、格點法、最陡爬坡等方法。為了較為直觀地展示整個搜索結果，本文采用了直接搜索法。

4 資本存量估計結果

4.1 數據來源

中國數據：本文估計采用的數據包括資本形成總額、投資價格指數、實際GDP、經濟活動人口數、固定資產投資額、投資價格指數和折舊額。鑒于李賓[7]提供的數據被采用較多，因此2009年前上述各變量亦主要采用該文數據。而對于其后年份的數據則從相應年份的中國統計年鑒中補充。同時，對于折舊的處理也采用該文的方法，即用固定資本形成總額減去當年的折舊額。同時，由于1993年以前國家統計局未公布折舊額，基于數據的可得性，本文的時間窗口選擇為1993—2015年。另外，所有變量均折算為2010年價格。

美國數據：美聯儲官網提供了歷年的資本存量、GDP、勞工就業人數統計數據。本文選擇該網站公布的按2011年價格計算的GDP、資本存量數據，勞動力數據根據所公布的按季節調整的就業人數取季度平均值作為該年份就業人數。

4.2 中國資本存量估計結果

參考現有文獻1993年資本存量估計值分布，并考慮迭代過程中的數據溢出問題。模型（10）初始值選取區間為[100,3000]百億元，選擇了多個初始值，包括100億元和2000億元，代入模型（10）進行1000次迭代估計。迭代收斂速度視初始值大小，通常在迭代17～23次后收斂于471百億元，與已有文獻的估計差異較大。同時，區間內不同初始值的選取對于估計結果沒有影響。模型（11）的初始值選取區間為[100,1500]，通常在迭代70～90次后收斂。利用模型（14）和模型（16）估計時，設定搜索區間為[100,3000]，步長10。結果模型（14）的估計值為1380，接近張軍和章元[1]的估計值。由此計算出的資本產生比在2.6～3.7之間。并且資本產出在1993—1997年不斷下降，此后至2004年緩慢上升，然后至2007年略快下降，2008開始加速上升，意味著資本產出效率的下降。而模型（16）未能給出有效估計值。同時也意味著，90年代以來在改革和金融危機的影響下，中國的資本產出比變動較明顯。表1給出了中國資本存量估計結果。

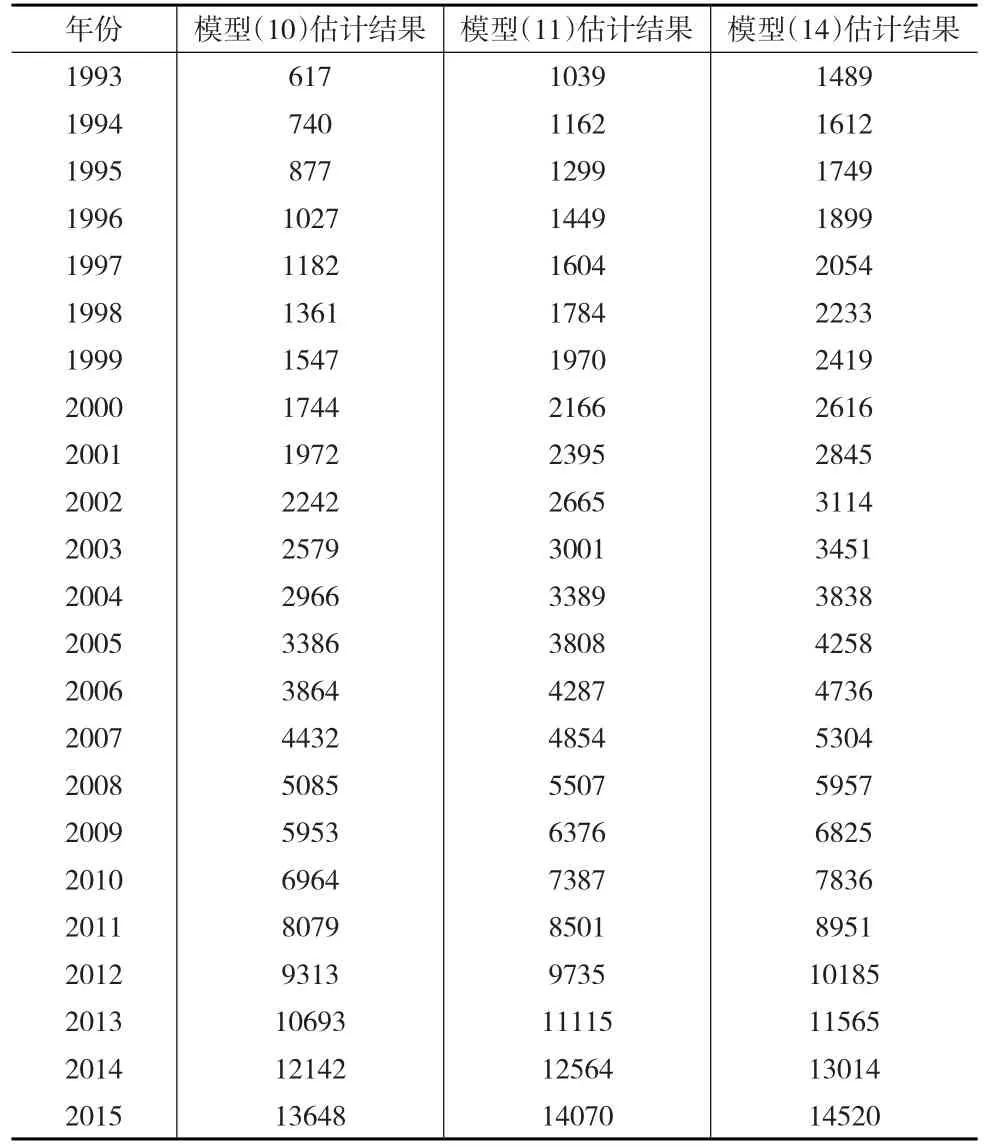
表1 中國資本存量估計所用數據及估計結果 （單位：百億元）

4.3 穩健性檢驗

這里選擇采用美國公布的數據來檢驗本文所介紹估計方法的可靠性。鑒于美國的數據都為1階單整，因此不使用模型（10）。具體而言，先使用官方公布的按照2011年價格計算的1950—2014年的資本存量數據差分得到歷年的凈投資It。再依據模型（11）、模型（14）和模型（16），設定不同初始資本存量進行估計。另外，模型（11）的初始值選取區間為[1000000,7000000]，通常迭代15次左右收斂于4125183百萬美元。模型（14）和模型（16）的初始資本存量K0的搜索區間為[1000000,10000000]，搜索步長為10000。并且，考慮模型設定可能與實際情況并不完全一致，因此模型中真實的α和β的絕對值可能并不相同。所以，實際進行搜索估計時，對于模型（14）和模型（16）分別根據（-α/β）和（α/β）選擇能夠使α和β最為接近的初始資本存量。

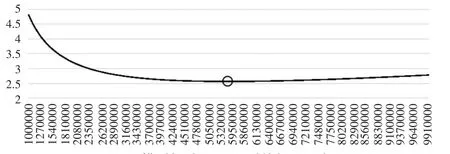
圖1 模型（14）不同 K0時的（-α/β）

圖1和圖2給出了不同初始資本存量時，對應的（-α/β）和（α/β），并標出了極值點位置。其中模型（14）的估計顯示，初始資本存量選擇5480000較合理，而模型（16）的估計顯示資本存量選擇應為5520000，因此這兩個模型估計的結果非常接近。而美國官方公布的1950年資本存量估計值為5680000。在凈投資數據可得的條件下，因為資本存量估計值的差異主要在于基期資本存量，所以可以認為模型（14）和模型（16）得到的估計值較為準確。另外，與對中國資本存量估計類似的是，通過搜索得到的估計值要高于通過高斯牛頓法得到的估計值。

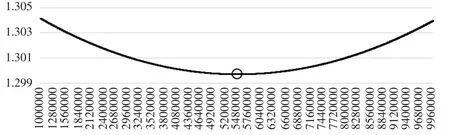
圖2 模型（16）不同 K0時的α/β

5 結論

本文通過對經濟增長模型的轉換，提出了對中國資本存量進行非線性估計的思路和模型。根據對經濟增長模型的不同處理，分別采用高斯牛頓法和直接搜索的方法進行了資本存量估計。結果發現：一階差分后的高斯牛頓法估計值與現有文獻估計值較為吻合，但是估計收斂速度較慢。而二階差分后的估計值收斂很快，但是估計值明顯低于近期文獻的估計值。這種情況可能與數據質量，以及差分過程中的信息丟失有關。而采用直接搜索得到的估計值高于已有文獻的估計值；另外，本文還利用美國官方公布的資本存量檢驗了本文提出的估計方法，發現直接搜索法能夠得到比較準確的估計值，而高斯牛頓法估計值相比直接搜索得到的估值小，與對中國資本存量的估計情況一致。