2018年全國高考數學考綱關鍵詞解讀及預測分析(1)
——三角、數列、立體幾何
■北京市第十二中學高中部 高慧明
本刊特邀欄目專家簡介:
高慧明 首屆全國十佳班主任,全國著名數學特級教師,國家教育部課程改革“全國先進工作者”,全國著名高考數學命題與考試研究專家,國家教育部“國培計劃”全國中小學教師培訓、班主任培訓、校長培訓特邀主講專家。受邀在全國各地做有關高考科學備考、班級管理等多個專題報告,場場好評如潮,在全國引起強烈反響。現任教于北京市第十二中學高中部。
一、三角中的關鍵詞——三角恒等變換
1.兩角和與差的三角函數公式。
(1)會用向量的數量積推導出兩角差的余弦公式。
(2)會用兩角差的余弦公式推導出兩角差的正弦、正切公式。
(3)會用兩角差的余弦公式推導出兩角和的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式,了解它們的內在聯系。
2.簡單的三角恒等變換。
能運用上述公式進行簡單的恒等變換(包括推導出積化和差、和差化積、半角公式,但不要求記憶)。
解讀:“兩角和與差的三角函數公式”的整體要求就是會推、會用。這是進行三角函數式化簡求值的主要依據,是高考命題的重點,要掌握一定的化簡技巧。看清要求——“積化和差、和差化積、半角公式,但對這三組公式不要求記憶”,所以不要做無用功哦。
命題預測:全國卷對三角的命題:小題一般主要考查三角函數的圖像與性質、利用誘導公式與和差角公式、倍角公式、正余弦定理求值化簡。大題主要以正、余弦定理為知識框架,以三角形為依托進行考查(注意在實際問題中的考查),或向量與三角結合考查三角函數化簡求值以及圖像與性質。
例1 (1)求函數f(x)=sinx·cosx+cos2x,x∈的值域;
(2)求函數f(x)=sinx+cos2x的值域。
解析:(1)f(x)=sinx·cosx+cos2x=
(2)f(x)=sinx+cos2x=-sin2x+sinx+1,令sinx=t,t∈[-1,1],函數變為y=-t2+t+1,值域為
例2 在△ABC中,角A,B,C的對邊分別為a,b,c,tanC=26。
(1)求cosC;
(2)若ab=20,且a+b=9,求△ABC的周長。
(2)因為ab=20,又因為a+b=9,所以a2+2ab+b2=81,所以a2+b2=41。所以c2=a2+b2-2abcosC=33,所以c=33。故△ABC的周長為a+b+c=9+33。
二、數列中的關鍵詞——通項公式、前n項和公式
1.掌握等差、等比數列的通項公式。
(1)掌握等差、等比數列的通項公式,了解其導出過程。
(2)掌握等差、等比數列的性質,特別是等差、等比中項問題,熟練掌握a1,an及公差d(或公比q)知三求二的運算,理解等差、等比數列中通項公式的特點,掌握求通項公式an的方法及有關最值的計算。
2.掌握等差、等比數列的前n項和公式。
(1)掌握等差、等比數列的前n項和公式,了解其導出過程。
(2)熟練掌握等差、等比數列前n項和公式的特點,掌握求前n項和Sn的方法及有關最值的計算。
解讀:數列的前n項和Sn與通項an的關系雖然沒出現在考綱中,但也是高考命題的一個重點內容。等差、等比數列在考綱中的要求與其在高考中的地位是相符的,均是命題的重點。等比數列求和的時候千萬要先考慮公比是否為1啊!還有,一定要能靈活運用等差、等比數列的性質解決相關問題。考綱中沒有明確提出掌握求通項公式an的方法,但是在具體考試的過程中,疊加、疊乘、待定系數還是有所涉及的,復習過程中應引起重視!數列是自變量為正整數的一類特殊函數,既然是特殊的函數,那么在確定數列最值的時候,自然也有它自身特殊的方法!
命題預測:全國卷對數列的命題:2個小題或1個大題,小題以考查數列概念、性質、通項公式、前n項和公式等內容為主,屬中低檔題;解答題以考查等差(比)數列通項公式、求和公式、錯位相減求和、簡單遞推為主。
例3 已知數列{an}滿足a1=2,an+1=an+p·2n-1+1(n∈N*,p為常數),a1,a2,a3-2成等差數列。
(Ⅰ)求p的值及數列{an}的通項公式;
(Ⅱ)設數列{bn}滿足明
解析:(Ⅰ)由a1,a2,a3-2成等差數列,知2a2=(a3-2)+a1,可得p=2。然后利用疊加的方法可求得an=2n+n-1。
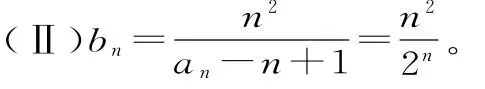
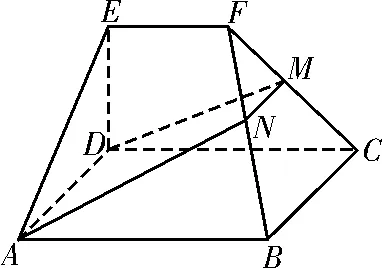
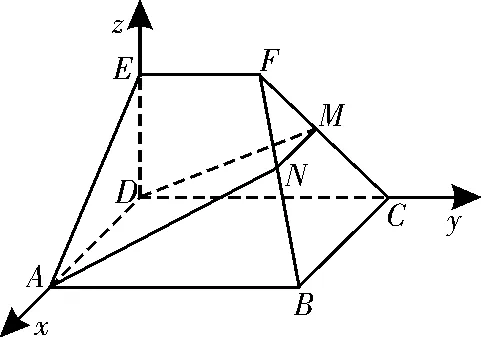
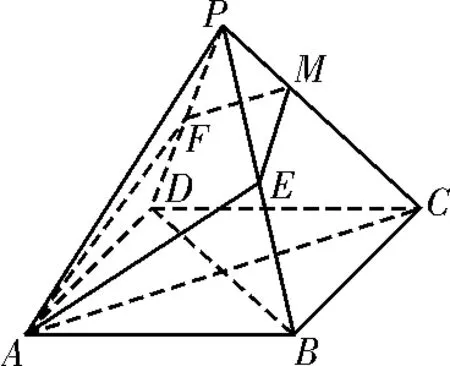
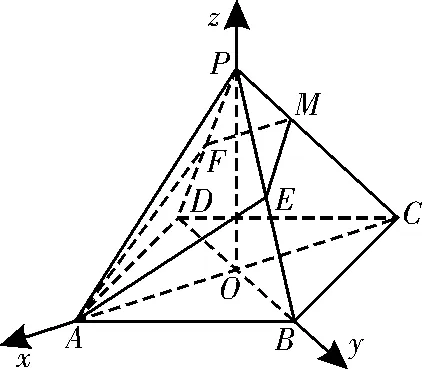
bn+1-bn<0,則n>1+2,即n≥4時bn+1 (Ⅰ)求數列{an}的通項公式; (Ⅱ)求Sn(n∈N*)的最值。 解析:(Ⅰ)當q=1時,-2S2=-4a1= 因為2S3≠-2S2+4S4,故q≠1。 由2S3=-2S2+4S4及Sn=,得q2·(2q2-q-1)=0,所以q=或q=1(舍去)。 (Ⅱ)由(Ⅰ)知: 綜上,Sn的最大值為,最小值為 1.理解空間位置關系的判定定理和性質定理。 判定定理:(1)平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行。 (2)一個平面內的兩條相交直線與另一個平面平行,則這兩個平面平行。 (3)一條直線與一個平面內的兩條相交直線垂直,則該直線與此平面垂直。 (4)一個平面過另一個平面的垂線,則這兩個平面垂直。 性質定理:(1)如果一條直線與一個平面平行,那么經過該直線的任一個平面與此平面的交線和該直線平行。 (2)兩個平面平行,則任意一個平面與這兩個平面相交所得的交線相互平行。 (3)垂直于同一個平面的兩條直線平行。 (4)兩個平面垂直,那么一個平面內垂直于交線的直線與另一個平面垂直。 解讀:空間線面位置關系的判斷經常以命題判斷的形式進行考查,判斷空間中的線面關系時,要把平面幾何中的知識與空間中的線面關系區分開來,不要熬成“大鍋飯”,亂成一團。 空間線面位置關系的推理與證明以平面圖形中的線線關系為基礎,所以要注意將空間中的問題通過平面的基本性質定理轉化為平面圖形中的問題來解決,這就是平面化的數學思想。 判定定理是我們證明空間平行與垂直關系的主要依據!證明時,條件要全,結論才能準確,亂改誤用條件,證明就會出現錯誤。 性質定理是我們處理已知條件中的空間線面關系的重要依據!一般是將面面關系轉化為線面關系,將線面關系轉化為線線關系。尤其要注意線面平行與面面垂直的性質定理,要準確把握定理中的條件,考題多通過改變條件或減少條件給出一些命題進行判斷,一定要牢記條件喲! 2.空間向量與立體幾何。 (1)掌握空間向量的線性運算及其坐標表示。 (2)掌握空間向量的數量積及其坐標表示,能用向量的數量積判斷向量的共線和垂直。 (3)理解直線的方向向量及平面的法向量。 (4)能用向量語言表述線線、線面、面面的平行和垂直關系。 (5)能用向量方法證明立體幾何中有關線面位置關系的一些簡單定理。 (6)能用向量方法解決直線與直線、直線與平面、平面與平面的夾角的計算問題,了解向量方法在研究立體幾何問題中的應用。 解讀:空間向量的要求都比較高,以“掌握”、“能用”為主,說明此處是高考命題的重點!作為解決空間線面關系、空間角與距離的求解的基本工具,一定要熟練掌握其基本運算。在建立空間直角坐標系時,一定要結合空間幾何體的結構特征,準確記憶公式,準確地用向量探究空間關系、用向量度量空間角。 命題預測:全國卷對立體幾何的命題:2道小題和1道大題,小題必考三視圖,一般側重于線與線、線與面、面與面的位置關系,以及空間幾何體中的空間角、距離、面積、體積的計算的考查,另外,特別注意對球的組合體的考查。解答題以平行、垂直、夾角、距離等為考查目標。幾何體以四棱柱、四棱錐、三棱柱、三棱錐等為主。 例5 如圖1,在幾何體ABCDEF中,底面ABCD為矩形,EF∥CD,AD⊥FC。點M在棱FC上,平面ADM與棱FB交于點N。 (Ⅰ)求證:AD∥MN; (Ⅱ)求證:平面ADMN⊥平面CDEF; (Ⅲ)若CD⊥EA,EF=ED,CD=2EF,平面ADE∩平面BCF=l,求二面角A-l-B的大小。 解析:(Ⅰ)因為ABCD為矩形,所以AD∥BC,所以AD∥平面FBC。又因為平面ADMN∩平面FBC=MN,所以AD∥MN。 (Ⅱ)因為ABCD為矩形,所以AD⊥CD。因為AD⊥FC,所以AD⊥平面CDEF。所以平面ADMN⊥平面CDEF。 (Ⅲ)因為EA⊥CD,AD⊥CD,所以CD⊥平面ADE,所以CD⊥DE。 圖1 由(Ⅱ)得AD⊥平面CDEF,所以AD⊥DE,所以DA,DC,DE兩兩互相垂直。 圖2 建立空間直角坐標系D-xyz,如圖2所示。不妨設EF=ED=1,則CD=2。設AD=a(a>0),由題意得A(a,0,0),B(a,2,0),C(0,2,0),D(0,0,0),E(0,0,1),F(0,1,1)。所以=(a,0,0)=(0,-1,1)。 設平面FBC的法向量為n=(x,y,z), 因為二面角A-l-B的平面角是銳角,所以二面角A-l-B的大小為45°。 【同步練習】 1.在△ABC中,角A,B,C的對邊分別為a,b,c,且atanC=2csinA。 (Ⅰ)求角C的大小; (Ⅱ)求sinA+sinB的取值范圍。 2.設{an}是首項為1,公差為2的等差數列,{bn}是首項為1,公比為q的等比數列。記cn=an+bn,n=1,2,3,…。 (Ⅰ)若{cn}是等差數列,求q的值; (Ⅱ)求數列{cn}的前n項和Sn。 3.如圖3,在正四棱錐P-ABCD 中,已知PA=AB,E,F分別為PB,PD的中點。 (Ⅰ)求證:AC⊥平面PBD; (Ⅱ)求異面直線PC與AE所成角的余弦值; 圖3 【參考答案】 2.(Ⅰ)因為{an}是首項為1,公差為2的等差數列,所以an=2n-1。因為{bn}是首項為1,公比為q的等比數列,所以bn=qn-1。所以cn=an+bn=2n-1+qn-1。因為{cn}是等差數列,所以2c2=c1+c3,即2(3+q)=2+5+q2,解得q=1。經檢驗,q=1時,cn=2n,所以{cn}是等差數列。 (Ⅱ)由(Ⅰ)知cn=2n-1+qn-1(n=1,2,…),所以 當q=1時,Sn=n2+n。 3.(Ⅰ)設AC∩BD=O,則O為底面正方形ABCD的中心。連接PO,因P-ABCD為正四棱錐,所以PO⊥平面ABCD。所以PO⊥AC。又BD⊥AC,且PO∩BD=O,所以AC⊥平面PBD。 (Ⅱ)因為OA,OB,OP兩兩互相垂直,如圖4,建立空間直角坐標系O-xyz。因為PB=AB,所以Rt△POB≌Rt△AOB,所以OA=OP。設OA=2,則A(2,0,0),B(0,2,0),C(-2,0,0),D(0,-2,0),P(0,0,2),E(0,1,1),F(0,-1,1)。故=(-2,1,1),=(-2,0,-2)。所以|cos|=即異面直線PC與AE所成角的余弦值為。 圖4 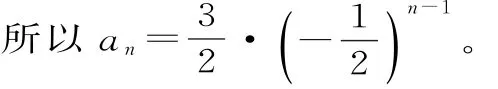
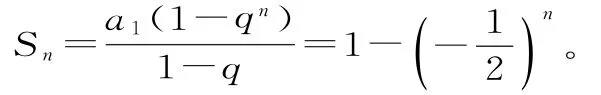
三、立體幾何中的關鍵詞——空間位置關系、空間向量