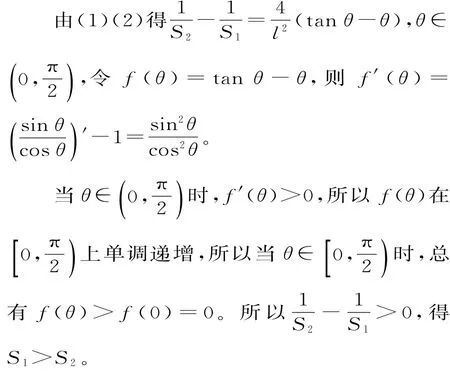求解三角形最值或范圍的“數學素養”
■山東省淄博市沂源縣第一中學 劉玉珍
三角中的最值或范圍問題實質上是變量的一種不等關系,是高考重點考查的內容,它對“三角恒等變形、三角函數圖像性質、正余弦定理的合理選用、構建函數模型,以及綜合應用所學知識解決問題”的素養要求較高。解決這一類問題的基本途徑:一是應充分利用三角函數自身的特殊性(如有界性);二是將三角中的最值或范圍問題通過構建目標函數,轉化為我們所熟知的求最值問題的思維方法。下面通過幾道高考模擬題,對三角中的最值或范圍問題求解中的“素養”作一歸納總結。
素養1:三角變換構建y=Asin(ωx+φ)+B的模型
例1 (2017年湖南省兩市九月調研)已知a,b,c分別是△ABC的三個內角A,B,C的三條對邊,且csinC-asinA=(b-a)·sinB。
(1)求角C的大小;
(2)求cosA+cosB的最大值。
解析:(1)由正弦定理角化邊湊出邊的齊次式表示角的余弦,因為csinC-asinA=(b-a)sinB,由正弦定理得c2-a2=b2-ab,即ab=a2+b2-c2,所以cosC=又因為C∈(0,π),所以
(2)利用內角和定理和題設條件降元構建正弦的復合函數求最值。
點擊素養:形如y=asinx+bcosx的函數可以利用輔助角公式轉化成y=a2+b2·sin(x+φ)的形式,再利用正、余弦函數的有界性求得最值,不是這種類型的可通過三角恒等變換變形為這種類型,本題利用題設和三角形的隱含條件降元變換得到。
素養2:借助余弦定理和三角變換構建三角函數模型y=Asin(ωx+φ)+B
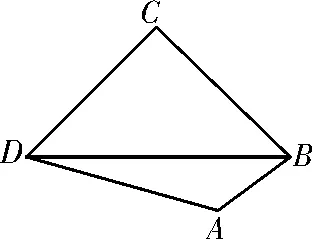
圖1
例2 (2017年第三
次全國大聯考新課標卷Ⅰ)如圖1,在四邊形ABCD中,AB=1,BC=2。
(1)若∠B=∠D,且CD=DA=3,求B;
(2)若CD⊥AD且CD=AD,求四邊形ABCD的面積S的最大值。
解析:(1)連接AC,在△ABC中,AB=1,BC=2,由余弦定理得AC2=AB2+BC2-2AB·BCcosB=5-4cosB。
在△ACD中,CD=DA=3,由余弦定理得AC2=CD2+DA2-2CD·DAcosD=6-6cosD。
(2)四邊形分解三角形構建其面積的目標函數,連接AC,則△ABC面積的S1=AB·BC·sinB=sinB。
由(1)得AC2=5-4cosB,又CD⊥AD且CD=AD,所以△ACD是等腰直角三角形,其面積為
所以四邊形ABCD的面積S=S1+S2的面積S的最大值為
點擊素養:四邊形面積的最值,合理分割化歸為兩個三角形的面積,借助三角形面積公式構建目標函數,利用正余弦復合函數的有界性求解,其中合理引入角參數,借助正余弦定理表示其邊長是求解的關鍵,如本題中選定B為主元,余弦定理表示AC2=5-4cosB溝通其關系。
素養3:巧設角參數構建y=Asin(ωx+φ)+B的模型
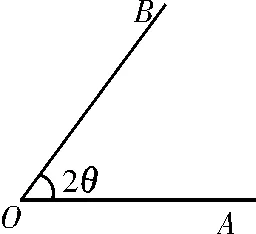
例3 (2017年第二次全國大聯考新課標卷Ⅲ)如圖2,已知扇形的圓心角∠AOB=,半徑為22,若C為弧上的一個動點(不與點A,B重合),則四邊形OACB的面積最大值為 。
解析:扇形中的有關問題,選圓心角為主元構建面積的目標函數。連接OC,并設∠AOC=θ,則∠BOC=

圖2

點擊素養:扇形的內接四邊形面積的最值問題,巧設圓心角為主元合理分割化歸為兩個三角形的面積,借助三角形面積公式構建目標函數,利用正余弦復合函數的有界性求解,凸顯三角的工具性、應用性及交匯性。
素養4:借助余弦定理構建二元變量模型用不等式求最值或范圍
例4 (2017年原創押題預測卷01(新課標卷Ⅲ))在△ABC中,角A,B,C的對邊分別為a,b,c,完成下列問題:
(1)若B=2A,求證:sinC=3sinA-4sin3A;

解析:(1)因為B=2A,所以C=π-3A。
所以sinC=sin(π-3A)=sin(A+2A)=sinAcos2A+cosAsin2A=sinA(1-2sin2A)+2sinAcos2A=sinA(1-2sin2A)+2sinA(1-sin2A)=3sinA-4sin3A,故sinC=3sinA-4sin3A。

點擊素養:余弦定理的實質是用三邊的二次齊次分式表示內角的余弦,于是,凡三邊滿足齊次的關系式降元代入余弦定理中可化歸二元變量,用不等式總可以求得角的余弦的取值范圍,進而求得角的取值范圍,有興趣的同學不妨試試,在△ABC中,滿足下列之一的條件都可以推出結論:(1)a,b,c成等差數列 ;(2)a,b,c成等比數列 ;成等差數列。
素養5:借助正余弦定理和面積公式構建二次函數求最值
例5 (2017屆浙江杭州地區重點中學高三上學期期中)在等腰△ABC中,AB=AC,AC邊上的中線BD長為6,則當△ABC的面積取得最大值時,AB的長為 。
解析:依據等腰三角形的特征,選腰長為主元,表示出頂角的余弦,進而構建面積的目標函數,同二次函數區間上的最值求解。根據題意,設AB=AC=2x,注意構成△ABD的條件,則AD=x(2 點擊素養:本題探究了 “等腰三角形中已知一腰中線的長度,可求等腰三角形面積最大值”的思維方法,其中利用幾何性質選腰長為主元,利用余弦定理和同角關系表示頂角的正弦,進而構建面積的函數關系式,凸顯了合理構建模型簡化求解實際問題的數學素養。 例6 (2017屆江蘇泰州中學高三上學期期中)圖3所示的是太湖的一個角形湖灣AOB,∠AOB=2θ(常數θ為銳角)。擬用長度為l(l為常數)的圍網圍成一個養殖區,有以下兩種方案可供選擇: 圖3 方案二:如圖5,圍成三角形養殖區OCD,其中CD=l。 (1)求方案一中養殖區的面積S1。 (2)求方案二中養殖區的最大面積S2。 圖4 (3)為使養殖區的面積最大,應選擇何種方案?并說明理由。 解析:(1)借助題設條件運用弧長公式建立函數關系。設OP=r,則l=r2θ,即r=,所 圖5 (2)借助題設運用余弦定理與基本不等式求解。設OC=a,OD=b,由余弦定理得l2=a2+b2-2abcos2θ,所以l2≥2ab-2abcos2θ,所以,當且僅當a=b時,“=”成立。所以 (3)注意兩個面積式子的分子相同的特點,取倒數作差構建含角和三角函數的新函數模型,運用導數的有關知識進行分析探求。 點擊素養:選角為主元可構建“含角和三角函數模型”求最值或范圍,注意角的取值范圍,對目標函數求導研究區間上的單調性進而求得,這是常用的通法“簡單且具有操作性”。素養6:構建“含角和三角函數”的模型用導數求解最值或范圍