立體幾何易錯題歸類剖析

■河南省商丘市第一高級中學 郭 永

立體幾何由三部分組成,一是空間幾何體,二是空間點、直線、平面的位置關系,三是立體幾何中的向量方法。高考在命制立體幾何試題時,對這三個部分的要求和考查方式是不同的。在空間幾何體部分,主要是以空間幾何體的三視圖為主展開,考查空間幾何體三視圖的識別判斷,通過三視圖給出的空間幾何體的表面積和體積的計算等問題,試題的題型主要是選擇題或者填空題,在難度上也進行了一定的控制,盡管各地有所不同,但基本上都是中等難度或者較易的試題。但是,有些題是看起來簡單做對卻很難。因為立體幾何有好多易錯題,所以我們對易錯題進行歸類剖析就很容易在該知識點的解答中拿高分。

易錯點1——求異面直線所成的角,若所成角為90°,容易忽視用證明垂直的方法來求夾角大小這一重要方法

例1 在三棱柱ABC-A1B1C1中,若AB=2BB1,則AB1與C1B所成角的大小為( )。

A.60° B.90° C.105° D.75°

易錯點分析：忽視垂直的特殊求法導致方法使用不當而浪費很多時間。

解析：如圖1,D1,D分別為B1C1,BC的中點,連接AD,D1C。設BB1=1,則AB=2,則AD為AB1在平面BC1上的射影。又BE=BE2+BD2-2BE·BD·所以∠BED=90°,所以AB1與C1B垂直。

圖1

知識點歸類點撥：求異面直線所成的角、直線與平面所成的角和二面角時,對特殊的角,如90°,可以采用證明垂直的方法來求之。

易錯點2——對幾何體的概念不清,找不出空間幾何體定義的關鍵要素

例2 設有四個命題：①底面是矩形的平行六面體是長方體;②棱長都相等的直四棱柱是正方體;③有兩條側棱都垂直于底面一邊的平行六面體是直平行六面體;④對角線相等的平行六面體是直平行六面體。

其中真命題的個數是( )。

A.1 B.2 C.3 D.4

易錯點分析：不能理清各種棱柱之間的聯系與區別。

解析：命題①是假命題。因為底面是矩形的直平行六面體才是長方體。底面是矩形,側棱不垂直于底面,這樣的四棱柱是斜平行六面體。命題②是假命題。底面是菱形,底面邊長與棱長相等的直四棱柱不是正方體。命題③是假命題。因為由兩條側棱垂直于底面一邊不能推出側棱與底面垂直。命題④是真命題,如圖2所示,平行六面體ABCDA1B1C1D1中所有對角線 相 等,對 角 面B1BDD1是平行四邊形,對角線BD1=B1D,所以四邊形B1BDD1是矩形,即BB1⊥BD,同理四邊形A1ACC1是矩形,所以AA1⊥AC,由AA1∥BB1知BB1⊥底面ABCD,即該平行六面體是直平行六面體。故選A。

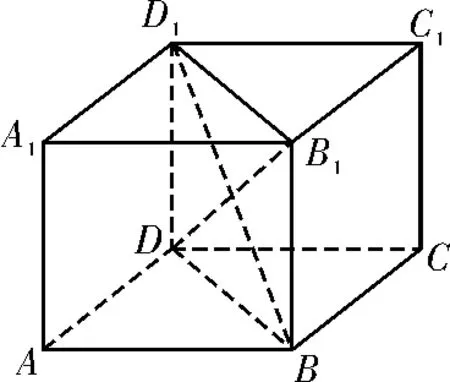
圖2

知識點歸類點撥：解這類選擇題的關鍵在于理清各種棱柱之間的聯系與區別,要緊扣底面形狀及側棱與底面的位置關系來解題。

易錯點3——對經度和緯度兩個概念容易混淆,弄不清楚經度是二面角,緯度是線面角

例3 如圖3,在北緯45°的緯線圈上有A,B兩點,它們分別在東經70°與東經160°的經度上,設地球的半徑為R,求A,B兩點的球面距離。

解析：設北緯45°緯線圈的圓心為O1,地球中心為O,則∠AO1B=160°-70°=90°,∠OBO1=45°,OB=R,O1B=O1A=R,AB=R,連接AO,AB,則AO=BO=AB=R,所以∠AOB=。故A,B兩點間的球面距離為

圖3

知識點歸類點撥：數學上,某點的經度是經過這點的經線與地軸確定的平面與本初子午線(0°經線)和地軸確定的半平面所成的二面角的度數。某點的緯度是經過這點的球半徑與赤道面所成的角的度數。

易錯點4——對于常見幾何體的體積計算公式,特別是棱錐、球的體積公式容易忽視公式系數,導致出錯

例4 如圖4,已知斜三棱柱ABCA1B1C1的底面△ABC是直角三角形,∠C=90°,BC=2cm,B1在底面上的射影D恰好是BC的中點,側棱與底面成60°角,側面AA1B1B與側面BB1C1C所成角為30°,求斜棱柱的側面積與體積。

易錯點分析：B1在底面ABC上的射影D為BC的中點,提供了線面垂直,即B1D⊥平面ABC。又∠C=90°,即AC⊥BC,可以得到AC⊥平面BB1C1C。利用這兩個線面垂直關系,可以方便地找到條件中的線面角以及二面角的平面角。

解析：因為B1在底面ABC上的射影D為BC的中點,所以B1D⊥平面ABC。所以∠B1BD為側棱B1B與底面ABC所成的角,即∠B1BD=60°。

因為∠C=90°,即AC⊥BC,又AC⊥B1D,所以AC⊥平面BB1C1C。過點A作AE⊥B1B于點E,連接CE,則CE⊥B1B。

所以∠AEC是側面AA1B1B與側面CC1B1B所成二面角的平面角,所以∠AEC=30°。

在Rt△CEB中,因為∠CEB=60°,BC=2,所以CE=3。

在Rt△ACE中,因為∠CEA=30°,CE=3,所以AC=ECtan30°=1,AE=2AC=2。

圖4

在Rt△B1DB中,∠B1BD=60°,BD=BC=1,所以BB1=2BD=2,B1D=BB1sin60°=3。

所以S側=CE·BB1+AE·BB1+AC·AA1=(3+2+1)×2=2(3+3)(cm2)。

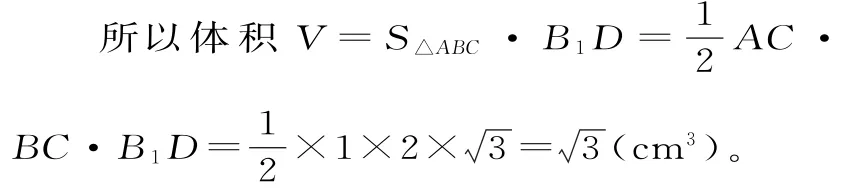
知識點歸類點撥：計算簡單幾何體的體積,要選擇某個面作為底面,選擇的前提條件是這個面上的高易求,本例中的△ACE是斜棱柱的一個截面,而且有側棱與該截面垂直,這個截面稱為斜棱柱的直截面,我們可以用這個截面把斜棱柱分成兩部分,并且用這兩部分拼湊成一個以該截面為底面的直棱柱,斜棱柱的側面積等于該截面的周長乘以側棱長,體積為該截面的面積乘以側棱長。