風電葉片疲勞試驗損傷在線評估的研究

烏建中，葉國忠

（同濟大學機械與能源工程學院,上海201804）

0 引言

風電葉片是風力發電機組的重要組成部分，其性能對整個機組的運行產生重大影響。資料顯示，由交變載荷產生的疲勞破壞約占葉片失效總數的80%[1]，是葉片失效的主要原因，因此需對新型葉片進行疲勞加載試驗。為了評估疲勞試驗后結構的損傷程度，傳統的做法是采集并保存試驗過程中的載荷數據，待試驗結束后進行疲勞損傷分析[2]。該做法無法保證在設計載荷循環次數下達到目標損傷，為確保疲勞試驗效果，一般需要適當增加載荷循環次數，造成不必要的能量損耗并延長試驗臺占用時間，影響效率。童第華等人雖在文中提及利用Markov矩陣法進行疲勞損傷計算基本可在數據采集階段實時完成，但未給出具體做法[3]。針對上述做法無法實時評估葉片損傷的局限性，本文設計一種風電葉片疲勞試驗損傷實時評估系統。該系統可在疲勞加載過程中，根據葉片表面的應變數據實時評估葉片各部位的損傷程度，為及時調整加載參數和判斷何時達到試驗指標提供依據。

（98）齒萼羽苔 Plagiochila hakkodensis Steph.熊源新等（2006）；楊志平（2006）

1 風電葉片疲勞加載系統

風電葉片疲勞加載系統如圖1所示，將葉片一端固定在塔筒上，在葉片上安裝激振器對其進行激勵，使葉片產生上下擺動。在葉片主要截面上布置應變傳感器，采集加載過程中葉片表面的應變數據，用于計算疲勞損傷。

《中國互聯網發展報告2018》顯示，2017年，中國數字經濟總量達到27.2萬億元，占GDP比重達到32.9%，數字經濟對GDP增長貢獻達55%。其中，數字經濟對服務業、工業和農業的滲透率分別達到32.6%、17.2%和6.5%。數字技術不僅改變著人們的生活，也改變著產業生態。

圖1 風電葉片疲勞加載系統簡圖

2 疲勞損傷理論和載荷許用循環次數確定

對葉片進行等幅疲勞加載時，材料承受載荷與載荷許用循環次數之間的關系通過S-N曲線來描述，如圖2所示。金屬材料的S-N曲線一般由試驗測定，但對于葉片的復合材料而言，試驗數據較少，一般通過經驗方程描述。工程上最常用的是冪函數形式的經驗方程，即

2組治療后的Scr和BUN水平高于且GFR水平低于治療前(P<0.05)；治療前后，2組Scr、BUN和GFR水平差異均無統計學意義(P>0.05)，見表2。

式中：S為載荷幅值；N為載荷許用循環次數；m為S-N曲線的斜率參數（對于葉片復合材料，取m=10）；RK，A為載荷許用循環次數N=1時的載荷強度（靜載荷強度）。

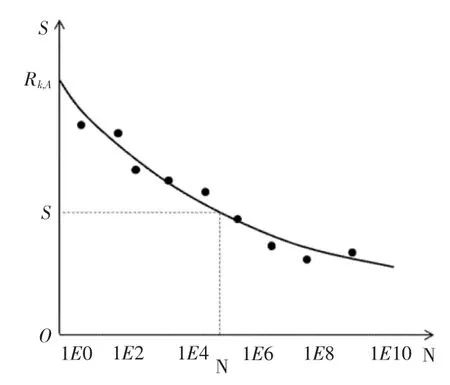
圖2 材料S-N曲線

上述S-N曲線僅考慮了載荷幅值對疲勞壽命的影響，實際加載過程中，需同時考慮載荷均值和幅值對葉片壽命的影響，利用圖3所示Goodman圖確定等效載荷[4]。為防止試驗過程中葉片發生災難性破壞，對最大載荷均值和最大載荷幅值分別取安全系數γMa＞1和γMb＞1，則實際S-N曲線向下平移，如曲線2所示，其表達式為：

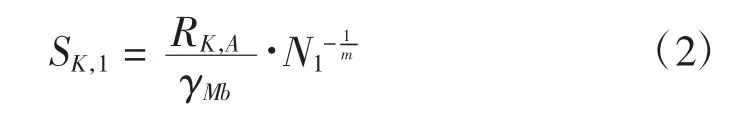
若某一次載荷循環中的載荷峰谷值分別為Smax和Smin，則相應地載荷均值SK，M和SK，A載荷幅值可以表示為：

大內三品侍衛李駟峋，江湖上人稱“三眼李耳”的高手，居然自焚而死，死時渾身散發異香。這條驚人消息如同插上翅膀，迅速傳遍京城。

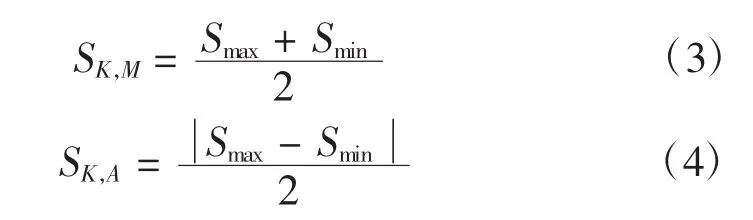
進行風電葉片疲勞加載試驗時，葉片某截面的彎矩通過該截面的應變測量值乘以靜態標定系數求得，未經處理的彎矩波形中包含了很多噪聲信號，如圖4（a）所示。為從彎矩波形中獲取彎矩峰谷值序列，須對彎矩波形進行最小二乘二次擬合。

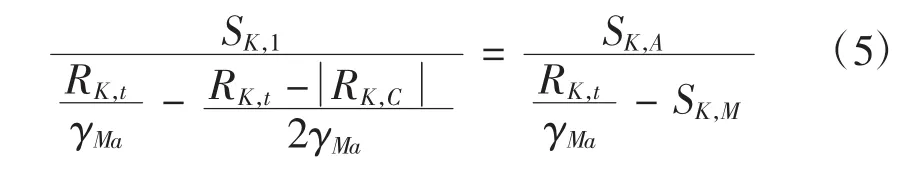
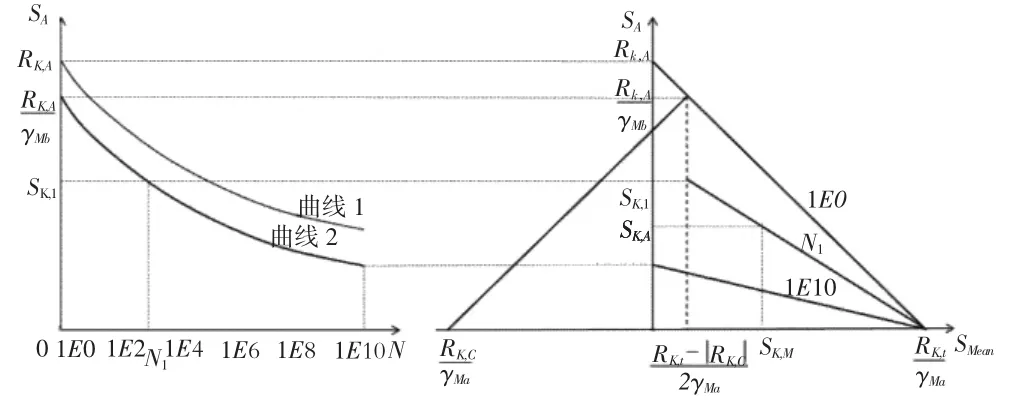
圖3 材料S-N曲線和Goodman圖對應關系

結合式（2）、（3）、（4）、（5）可得，載荷許用循環次數為：

式中，Rk，t為材料的拉伸強度特征值；Rk，c為材料的壓縮強度特征值；γMa為材料的局部安全系數（靜強度）；γMb為材料的局部安全系數（疲勞強度）；

3 由Markov頻次矩陣計算疲勞損傷

疲勞載荷歷程中的每個峰谷點，都是一種特定的載荷狀態，載荷歷程就是載荷狀態的不斷變換。利用Markov頻次矩陣計算疲勞損傷，即求取一段載荷歷程中不同載荷循環出現的頻次，并據此累計該段載荷歷程造成的總損傷。Markov頻次矩陣是一個二維方陣，如表1所示，其第i行第j列的元素nij表示前一次載荷為si，后一次載荷為sj的情況在特定數據段中總共出現了nij次。

表1 Markov頻次矩陣

由式（13）可求得擬合曲線的a，b，c三個參數。經過n/m次（n為載荷歷程數據段長度）擬合計算，可將圖4（a）所示的含噪曲線轉化為圖4（b）所示的由二次曲線拼接而成的平滑曲線。對該曲線求導取極值可獲得彎矩的峰谷值序列，為確保邊界處的峰谷值能求出，取前段波形的最后mλ/4個數據疊加到后一段波形中，并剔除重復的峰谷值，得到結果如圖4（c）。

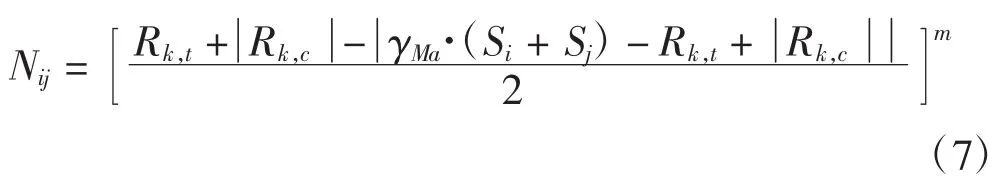
每次從彎矩波形中讀取一段數據段（xi，yi）（i=1，2，…，m），為保證擬合曲線峰谷值位置的準確性，應滿足數據長度2≤m≤mλ/4（mλ為兩個最近波峰之間的數據長度）。利用二次曲線p（x）=a+bx+cx2擬合數據段，則數據段與擬合曲線的均方誤差可表示為：

則次載荷循環造成的疲勞累積損傷為：

一段載荷歷程造成的疲勞累積損傷：

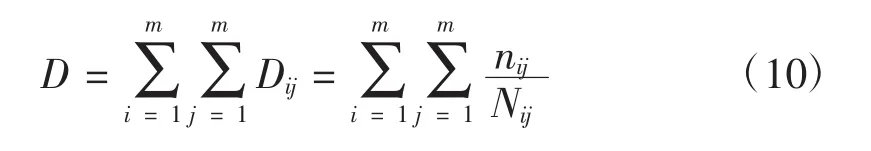
4 葉片載荷數據實時處理

其等效循環載荷SK，1可在Goodman圖中利用相似三角形求得：

根據Miner線性疲勞累積損傷理論[5]，單次載荷循環造成的相對疲勞損傷可以表示為：

由多元函數極值原理，均方誤差的極小值minQ（a，b，c）應滿足:

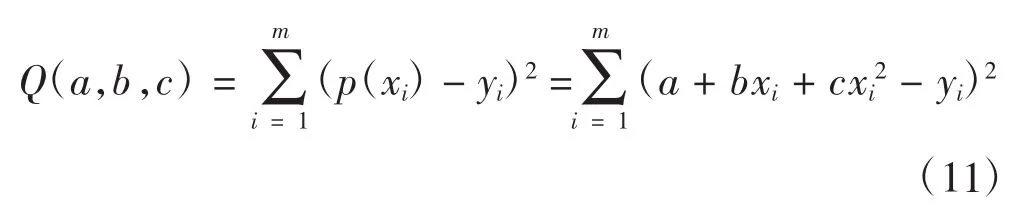
抽煙男不可思議地看了看自己的腹部，一股又一股鮮紅的血液涌了出來，噴濺在地上，他“啪”的一聲摔倒在血泊中。

根據Markov頻次矩陣中的每一個元素對應的載荷變化情況確定相應的許用循環次數：

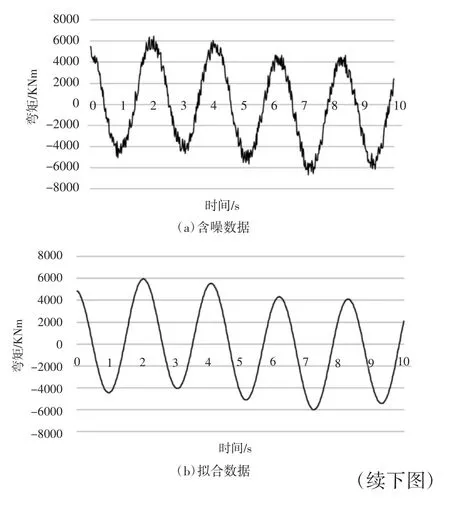
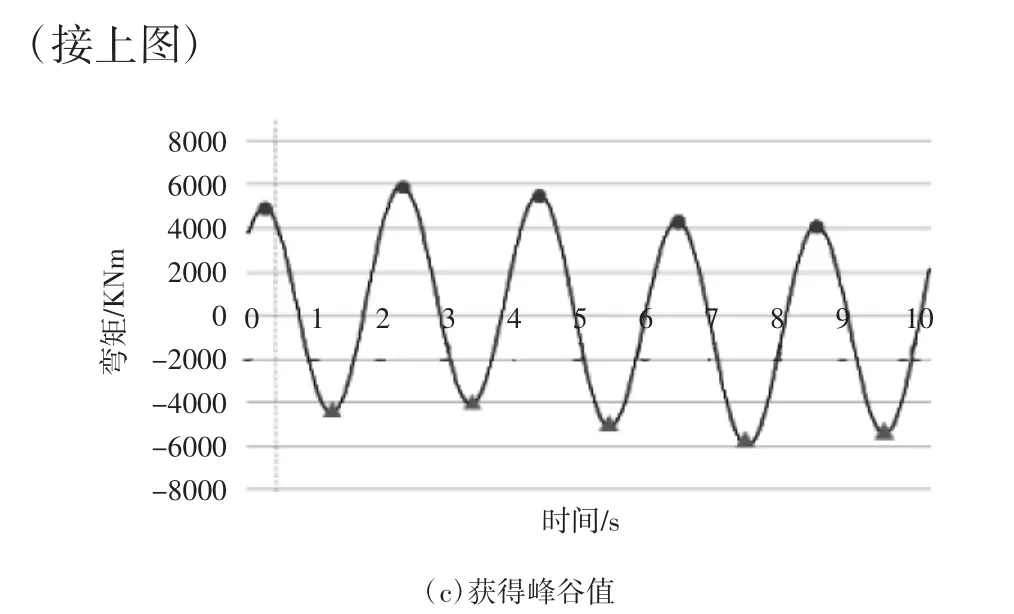
圖4 載荷數據預處理

5 葉片疲勞損傷實時評估軟件程序設計

采用“生產者-消費者”設計模式來實現載荷數據的在線處理。通過LabVIEW和某型動態應變儀的上位機軟件共享物理內存來獲得應變數據，存儲在緩沖區中。數據處理程序每隔一定時長從緩沖區中讀取數據并進行損傷計算，并將結果寫入數據庫。若主要截面有12個，應變儀采樣頻率為50Hz，數據處理程序每隔10 s讀取一次數據，則單次需要處理的數據量為6 000個，處理時間t＜1 s，不會造成緩沖區溢出。軟件實現流程如圖5所示。

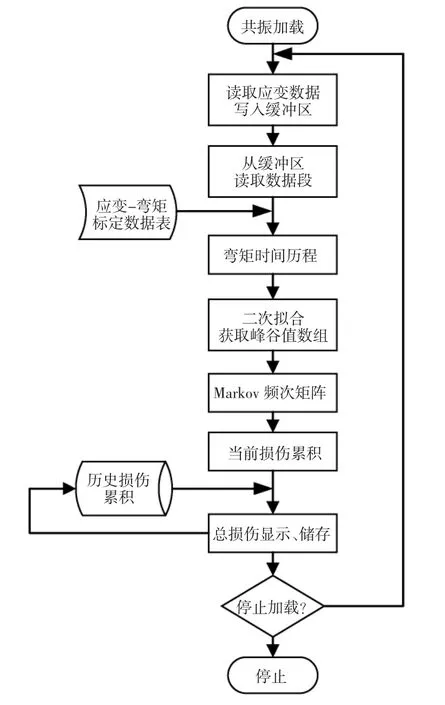
圖5 葉片疲勞損傷實時評估系統軟件實現流程

6 實驗效果

為驗證風電葉片疲勞試驗損傷實時評估系統的準確性，對某型56.5 m葉片疲勞加載試驗的損傷分別進行實時處理和后處理，兩者結果對比如圖6所示，圖6中PS面為葉片迎風面，水平固定時朝上，SS面為背風面，水平固定時朝下。可看出，實時處理的結果和后處理的結果基本吻合，但各截面實時處理的結果普遍比后者偏高2%左右。這是由于進行后處理時，為了提高程序運行效率，對彎矩峰峰值小于額定值80%的數據進行了舍棄，而實時評估系統則考慮了所有載荷造成的損傷。

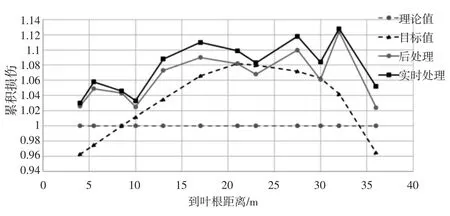
圖6 某型56.5 m葉片疲勞試驗損傷對比

7 結論

（1）對風電葉片疲勞試驗損傷數據進行實時處理，每次處理的數據量非常有限，降低了對計算機運算能力的要求；

（2）風電葉片疲勞試驗中的載荷變化近似符合正弦曲線，通過二次擬合后可由求導方式直接獲得載荷峰谷值，不必進行“雨流法”循環計數；

“在這樣的崗位，你得隨時面對新問題，也要隨時解決，只有一股干活的蠻勁而沒有文化是不行的。”領導對董松江說。

（3）進行風電葉片疲勞損傷實時評估可以在疲勞試驗過程中及時獲知葉片各截面損傷情況，且整個加載周期的累計結果和載荷數據后處理的結果基本一致，具備及時性和準確性。