不完全無誤判金標準下二重抽樣設計中樣本量的確定
邱世芳,曾小松
(重慶理工大學 理學院, 重慶 400054)
1 背景
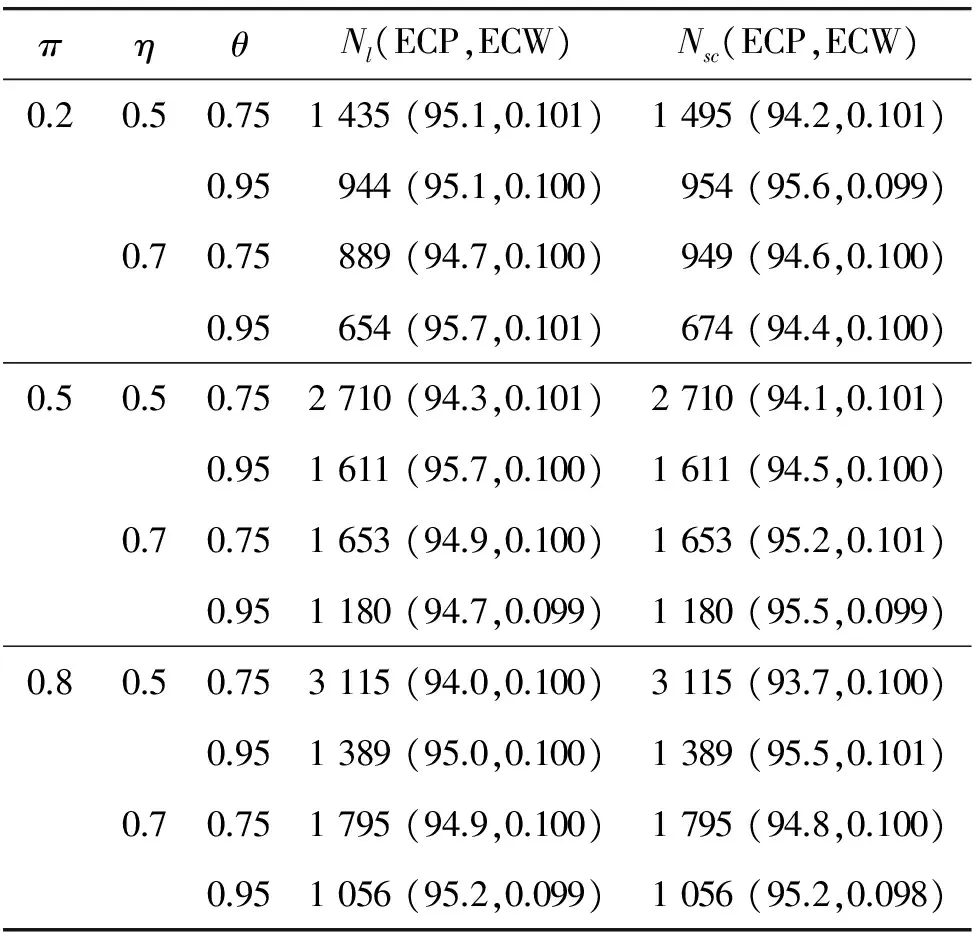
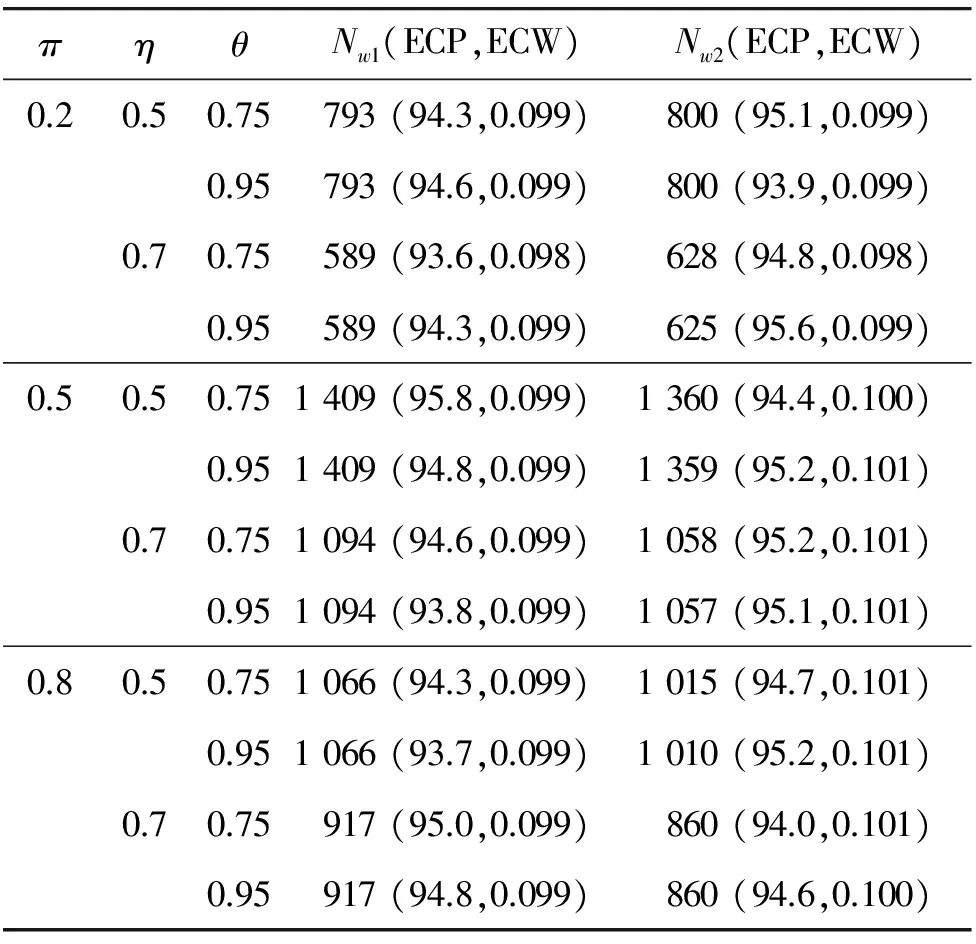
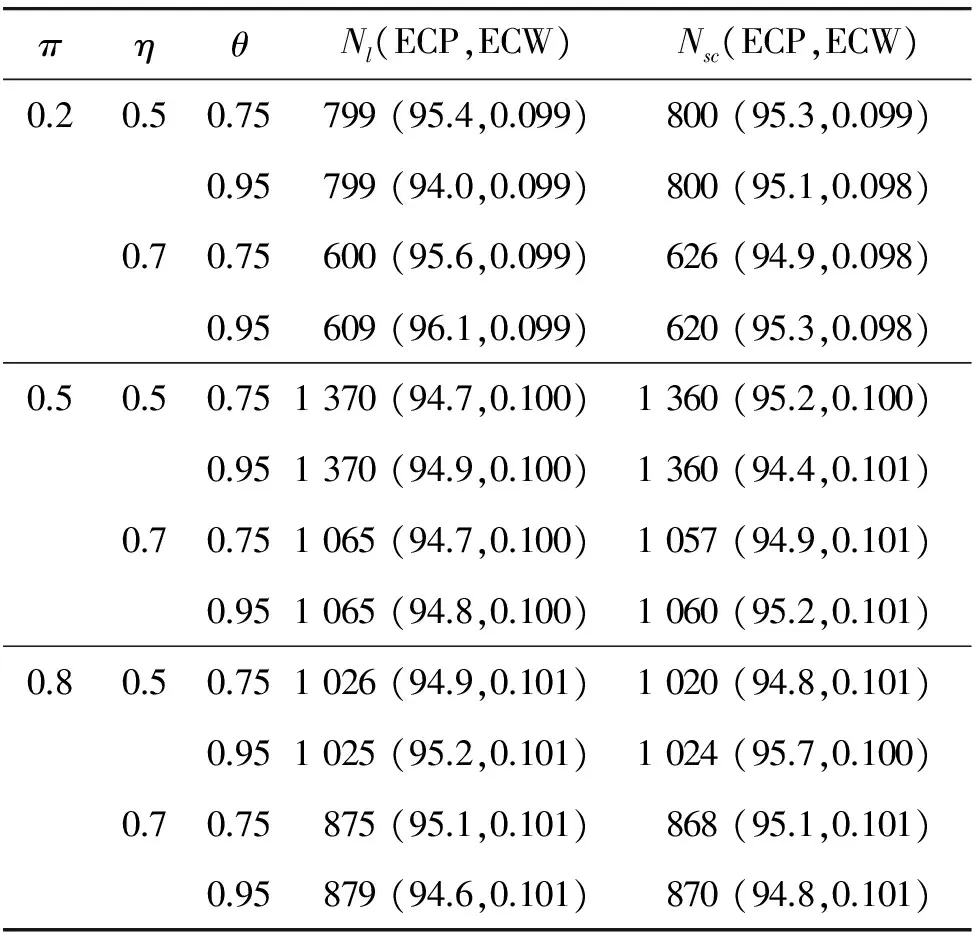
在生物醫學和流行病學研究中,為了分析一種疾病的流行率,人們通常使用價格便宜的篩檢方法對感興趣的個體是否感染這種疾病進行第1次臨床診斷。但是,這種篩檢方法經常導致因不可忽略的診斷誤差而出現存在誤判的分類數據;另一方面,雖然可以選擇一種完全準確的金標準檢驗,但是這種檢驗具有價格昂貴、耗時長而且對檢驗個體有副作用等不足。為了克服這兩種方法的不足,常采用二重抽樣方法獲得部分核實數據,即從感興趣的總體中隨機抽取N個個體,對每個個體都使用篩檢方法進行診斷檢測,然后再從中隨機抽取n(n 在完全無誤判的金標準存在時,已有文獻對基于部分核實數據的統計推斷問題進行研究。例如:Boese[4]對二重抽樣設計下有假陽性錯誤分類時,提出了關于二項分布參數的幾種基于似然的近似區間估計;Morvan[5]對篩檢過程的準確性以及兩階段調查中疾病流行率的修正估計的準確性提出了兩種評價方法;對于單個樣本情形,Tang等[3]基于疾病的流行率提出了有實際意義的統計假設,并對此假設考慮了Score檢驗統計量、似然比檢驗統計量以及兩種Wald型檢驗統計量,從大樣本的角度考慮了漸近的檢驗過程以及從小樣本的角度考慮了近似非條件的檢驗過程;Tang等[6]基于上述檢驗統計量提出了關于疾病流行率的12種區間估計方法;Qiu等[7]分別從顯著性檢驗的角度和置信區間的角度研究了疾病流行率顯著性檢驗的樣本量的計算公式。對于兩組獨立樣本情形,Tang等[8]基于疾病流行率之差考慮了兩組獨立樣本下疾病流行率的顯著性差異的假設檢驗問題,分析了多種檢驗統計量(如Score或者Score型檢驗)的大樣本的漸近檢驗過程和小樣本的近似非條件的檢驗過程,并從檢驗功效的角度研究了樣本量的確定問題; Qiu等[9]基于比例差對不同組的流行病治愈率的等價性評價進行了研究,從置信區間的角度提出了等價性檢驗中基于比例差的置信區間的估計方法。 以上內容都是基于有完全無誤判金標準存在時部分核實數據的研究。事實上,完全無誤判的金標準通常是不存在的,接受核實驗證的個體通常接受的是不完全無誤判金標準檢驗。當這種不完全金標準檢驗比篩檢有更高的敏感度和特異度時,這樣的二重抽樣設計仍然可以降低統計推斷的偏差,因而基于不完全無誤判金標準下的核實數據的統計推斷更具有現實意義和實際研究價值。一個典型的例子是Nedelman[10]利用二重抽樣方法對瘧疾病的流行率進行了研究,根據年齡的不同將總體分為了7個年齡組。首先初級的顯微鏡醫生對每一個年齡組的個體進行檢驗,然后從中隨機抽取一部分個體再接受高級顯微鏡醫生的檢驗,從而得到部分核實數據。在此研究中,高級顯微鏡醫生雖然比初級醫生有更高的敏感度,但是他們的檢驗仍然有誤判可能性。基于這樣的部分核實數據,Qiu[11]在沒有假陽性假定下對疾病流行率的區間估計進行了研究,考慮了兩種模型下的多種有效的區間估計方法。但是,實驗樣本量的確定問題是實際醫務工作者最為關心的問題之一,而從區間估計的角度對該問題的研究還沒有文獻涉及,因此本文對不完全無誤判金標準下的二重抽樣設計中所需要的樣本量進行研究。 假設從感興趣的總體中隨機抽取N個個體并用篩檢方法進行檢驗,檢驗結果用變量J表示,J=1表示陽性,J=0表示陰性。然后從抽取的N個個體中再隨機抽取n個個體接受不完全無誤判金標準檢驗,檢驗結果用變量S表示,S=1表示陽性,反之則表示陰性。二重抽樣的數據結構如表1所示。 表1 二重抽樣的數據結構 假設D表示個體患病狀態變量,D=1表示患有疾病,反之表示正常。令π=Pr(D=1),η=Pr(J=1|D=1)和θ=Pr(S=1|D=1),即η和θ分別表示篩檢和不完全金標準檢驗的敏感度。本文考慮不存在假陽性誤判的情形,因而它們的特異度皆為1。 假定兩種檢驗方法滿足條件獨立性,即Pr(J,S|D)=Pr(J|D)Pr(S|D)時,Nedelman[10]提出了一種模型(記為模型1),其概率結構如表2所示。 表2 模型1的概率結構 令m=(n11,n10,n01,n00,x,y),則在此概率模型下m=(n11,n10,n01,n00,x,y)的似然函數為: L1(m;π,η,θ)=A1(πηθ)n11(π(1-η)θ)n10(πη(1-θ))n01(1-π(η+θ-ηθ))n00(πη)x(1-πη)y= A1πn-n00+xηn+1+x(1-η)n10θn1+(1-θ)n01(1-π(η+θ-ηθ))n00(1-πη)y 其中A1是與參數無關的常數,其對數似然函數為 l1(m;π,η,θ)=C1+(n-n00+x)logπ+(n+1+x)logη+n10log(1-η)+n1+logθ+ n01log(1-θ)+n00log(1-π(η+θ-ηθ))+ylog(1-πη) (1) 其中C1=logA1為常數。 令λ1=Pr(S=1|J=1),λ2=Pr(S=1|J=0)和p=Pr(J=1),則λ1=θ,λ2=π(1-η)θ/(1-πη),p=πη,因此對數似然函數(1)變為: l1(m;λ1,λ2,p)=C1+n11logλ1+n01log(1-λ1)+ n10logλ2+n00log(1-λ2)+(n+1+x)logp+(n+0+y)log(1-p) 則λ1、λ2和p的極大似然估計為: 由此易得到,當n11n00≥n10n01時,π、η和θ的極大似然估計分別為: (2) (3) 假定兩種分類器不具有條件獨立性時, Lie等[12]提出了一種模型(記為模型2),其概率模型結構如表3所示。 表3 模型2的概率結構 在此概率模型下m=(n11,n10,n01,n00,x,y)的似然函數為 L2(m;π,η,θ)=A2(π(η-1+θ))n11(π-πη)n10(π-πθ)n01(1-π)n00(πη)x(1-πη)y= A2πn-n00+x(1-π)n00ηx(1-η)n10(1-θ)n01(η+θ-1)n11(1-πη)y 其對數似然函數為: l2(m;π,η,θ)=C2+(n-n00+x)logπ+n00log(1-π)+xlogη+n10log(1-η)+ n01log(1-θ)+n11log(η+θ-1)+ylog(1-πη) (4) 其中A2和C2為與參數無關的常數。 在此模型下,由λ1、λ2和p的定義可得λ1=(η+θ-1)/η,λ2=π(1-η)/(1-πη)和p=πη。采用和模型1類似的方法可得π、η和θ的極大似然估計分別為: (5) (6) 本文假設核實驗證比例為κ,即在κ=n/N情況下考慮實驗樣本量的確定問題。 其中zα/2為標準正態分布的上α/2分位數。為了將置信區間寬度控制在2ω以內,當ω≤π時設zα/2σ=ω,否則π+zα/2σ=2ω。由此得到基于Wald檢驗的100(1-α)%置信區間寬度控制在指定寬度2ω所需的樣本量(即N),其計算公式為: (7) 其中:對于模型1有 對于模型2有 由此容易發現:在模型2下的樣本量與不完全無誤判金標準的敏感度無關。 3.2.1 基于限制性極大似然估計下方差的Wald置信區間 (8) 此方程組沒有顯示解,因此可通過一種迭代方法(如牛頓迭代法)獲得。 其中:a=π0(N-n00);b=N-y-n00+π0(N-n+0);c=b2-4a(x+n+1)。 在模型2下,有 3.2.2 基于似然比檢驗的置信區間 兩種模型下的似然比檢驗統計量為 3.2.3 基于Score檢驗的置信區間 對于模型1,Score函數為: 對于模型2, Score函數為: 則對于假設檢驗H0:π=π0的Score檢驗統計量為 或 其中I11的表達式見附錄。在原假設下Tsc漸近服從標準正態分布,因而基于Score統計量的(1-α)100%的置信區間[πl,πu]的上下限可利用迭代方法通過以下方程得到: Tsc=±z1-α/2 其中πl,πu分別對應方程中取“+”和“-”得到。 3.2.4 樣本量的求解算法 由于基于以上檢驗統計量Tw2、Tl和Tsc的置信區間都沒有顯表達式,因此考慮以下搜索算法獲得近似樣本量的估計: 步驟1 給定π,η,θ,N和κ的值,產生K組隨機樣本m=(n11,n10,n01,n00,x,y),其中:在模型1中,(n11,n10,n01,n00)~M(Nκ;πηθ,π(1-η)θ,πη(1-θ),π(1-η)(1-θ)+1-π);在模型2中,(n11,n10,n01,n00)~M(Nκ;π(η+θ-1),π(1-η),π(1-θ),1-π)。在兩種模型下(x,y)都服從二項分布B(N(1-κ),πη),其中M(·)表示多項分布。 步驟2 基于步驟1產生的每一個樣本,計算π的(1-α)100%置信區間,并通過K個置信區間寬度的平均值計算近似的區間寬度,記為2ω*(N)。 步驟3 若2ω*(N)小于(大于)2ω,那么減少(增加)N的值,重復步驟1和步驟2。 步驟4 重復步驟3直到近似的半區間寬度ω*(N)非常接近于給定的區間寬度ω,則N=minN:|ω*(N)-ω|≤0.001},即為滿足條件的近似樣本量。 通過以上搜索方法獲得的基于Tw2、Tl和Tsc的置信區間的樣本量公式分別記為Nw2、Nl和Nsc。 為了評價本文所提出方法的效果,考慮將置信水平1-α=0.95下的置信區間寬度的一半控制在ω=0.05下的樣本量的確定,并在估計的樣本量(即Nw1,Nw2,Nl和Nsc)下,通過模擬分別研究各置信區間的經驗覆蓋概率和經驗覆蓋寬度。假設核實比例即接受不完全金標準檢驗的個體比例κ=0.2,參數設置為π=0.2、0.5和0.8,由于不完全無誤判金標準檢驗不劣于篩檢方法,因而對于敏感度設置為η=0.5和0.7,θ=0.75和0.95,總共3(π的取值)×2(η的取值)×2(θ的取值)=12種參數組合進行蒙特卡洛模擬。 在給定參數組合下,估計出樣本量Nw1、Nw2、Nl和Nsc,在估計的樣本量下,產生2 000個隨機樣本m=(n11,n10,n01,n00,x,y),基于每個統計量計算相應的置信區間,從而得到置信區間的經驗覆蓋概率(ECP)和經驗覆蓋寬度(ECW)。模型1的模擬結果見表4,模型2的模擬結果見表5。 πηθNl(ECP,ECW)Nsc(ECP,ECW)0.20.50.751435(95.1,0.101)1495(94.2,0.101)0.95944(95.1,0.100)954(95.6,0.099)0.70.75889(94.7,0.100)949(94.6,0.100)0.95654(95.7,0.101)674(94.4,0.100)0.50.50.752710(94.3,0.101)2710(94.1,0.101)0.951611(95.7,0.100)1611(94.5,0.100)0.70.751653(94.9,0.100)1653(95.2,0.101)0.951180(94.7,0.099)1180(95.5,0.099)0.80.50.753115(94.0,0.100)3115(93.7,0.100)0.951389(95.0,0.100)1389(95.5,0.101)0.70.751795(94.9,0.100)1795(94.8,0.100)0.951056(95.2,0.099)1056(95.2,0.098) 表5 基于模型2的95%置信區間寬度控制在2ω=0.1下的近似樣本量、經驗覆蓋概率(%)和經驗區間寬度 πηθNl(ECP,ECW)Nsc(ECP,ECW)0.20.50.75799(95.4,0.099)800(95.3,0.099)0.95799(94.0,0.099)800(95.1,0.098)0.70.75600(95.6,0.099)626(94.9,0.098)0.95609(96.1,0.099)620(95.3,0.098)0.50.50.751370(94.7,0.100)1360(95.2,0.100)0.951370(94.9,0.100)1360(94.4,0.101)0.70.751065(94.7,0.100)1057(94.9,0.101)0.951065(94.8,0.100)1060(95.2,0.101)0.80.50.751026(94.9,0.101)1020(94.8,0.101)0.951025(95.2,0.101)1024(95.7,0.100)0.70.75875(95.1,0.101)868(95.1,0.101)0.95879(94.6,0.101)870(94.8,0.101) 模擬研究表明:在基于限制性極大似然估計下方差的Wald置信區間、似然比置信區間和Score置信區間確定的樣本量下,它們的經驗覆蓋概率接近事先給定的置信水平,且半區間寬度很好地控制在ω以內,因而基于這3種方法確定的樣本量準確有效。但是,在基于非限制性極大似然估計下方差的Wald置信區間確定的樣本量下,其經驗覆蓋概率不能保證其接近給定的覆蓋概率。其次,隨著患病概率的增大,要使95%的置信區間寬度控制在2ω以內,所需要的樣本量就越大,隨著兩種檢驗的敏感度的增大,所需的樣本量相應減少。通過對比4種方法可以看到:模型1基于非限制性極大似然估計下方差的Wald置信區間、似然比置信區間和Score置信區間確定的樣本量很接近,沒有顯著差別,只有當π比較小的時候相差較大,限制性極大似然估計下方差的Wald置信區間與其他3種方法相差較大;而模型2基于限制性極大似然估計下方差的Wald置信區間、似然比置信區間和Score置信區間確定的樣本量相差不大,沒有顯著差異,基于非限制性極大似然估計下方差的Wald置信區間與這3種方法所計算的樣本量大概相差40。最后,在相同的參數設置下,基于模型2所需要的樣本量通常比模型1要小。因此,當兩種檢驗不滿足條件獨立性時,應考慮模型2的統計分析。 首先,對于引言中的瘧疾數據,采用本文提出的方法進行研究。由于篇幅的限制,僅列出小于1歲的年齡組的分析結果,其他年齡組的結果不再一一列出。此年齡組的觀測數據為n11=165、n10=8、n01=7、n00=80、x=1736、y=799,即n=260、N=2795。通過數據易知:核實數據的比例約等于0.09,在模型1中參數π、η和θ的極大似然估計分別為0.712 7、0.957 8和0.959 3,在模型2中參數的極大似然估計分別為0.711 5、0.959 5和0.961 0。因此,在樣本量的估計中,令κ=0.1,π=0.70,η=0.95,θ=0.95,置信水平為95%,半區間寬度ω=0.05,利用本文提出的樣本量估計方法,分別得到兩種模型下的樣本量的估計值,并計算在估計的樣本量下95%置信區間的經驗覆蓋概率和經驗覆蓋寬度。在模型1下,Nw1=786,Nw2=846,Nl=816,Nsc=856,其經驗覆蓋概率(覆蓋寬度)分別為92.3%(0.097 7),96.1%(0.100 4),95.6%(0.100 3)和95.1%(0.100 7);在模型2下,Nw1=757,Nw2=800,Nl=799,Nsc=813,其經驗覆蓋概率(覆蓋寬度)分別為93.5%(0.097 6),95.1%(0.099 8),95.4%(0.098 7)和95.3%(0.101 4)。由此可見,要使95%的置信區間寬度控制在0.10內,現有的樣本量是滿足的。 其次,對Qiu等[7]使用的移植時年齡小于20歲的再生障礙性貧血患者數據進行分析,原始數據為:n11=6、n10=4、n01=3、n00=18、x=12、y=49,即n=31、N=92。在k=0.3,π=0.4,η=0.55,θ=0.75且置信水平為95%、半區間寬度ω=0.05下,基于4種方法在模型1下的樣本量分別為Nw1=1 424,Nw2=1 534,Nl=1 424,Nsc=1 454,模型2下樣本量分別為Nw1=866,Nw2=837,Nl=841和Nsc=840。 在有金標準的情況下(Qiu等[7])結果為:Nw1=650,Nw2=656,Nl=657和Nsc=665。通過比較可以看到:有金標準所需的樣本量比沒有金標準所需樣本量小,并且無論在哪種情況下現有的樣本量都不能使95%的置信區間寬度控制在0.10內。 本文在不完全無誤判金標準下,基于部分核實數據從置信區間的角度研究檢驗所需的樣本量,分別考慮了兩種Wald檢驗、似然比檢驗和Score檢驗4種方法在兩種模型下樣本量的確定情況,然后對這些方法進行模擬研究,通過經驗覆蓋率和區間寬度評價本文所提出方法的準確性。通過模擬結果發現:在相同的參數設置下,基于模型2所需樣本量比模型1小,且樣本量的大小與不完全無誤判金標準檢驗的敏感度θ無關。基于限制性極大似然估計方差的Wald檢驗、似然比檢驗和Score檢驗的樣本量公式具有良好的統計性質,在估計的樣本量下的置信區間的經驗覆蓋概率和經驗覆蓋寬度都很接近給定的置信水平和區間寬度,因而可推薦用于實際應用中。 模型1假設兩種檢驗滿足條件獨立性,這個條件在實際中不一定滿足,所以在實際應用時要先判斷用于診斷的檢驗方法是否滿足條件獨立性。模型2的假設在實際中同樣可能不成立,所以應根據具體實際情況來選擇相應的模型。通過對實際數據的分析可以看到:本文研究成果具有實際應用價值,可為醫務工作者提供指導。本文從經典的頻率統計方面對樣本量的問題進行研究,在未來的研究中還可考慮采用貝葉斯等方法。 [1] TENENBEIN A A.A double sampling scheme for estimating from binomial data with misclassifications[J].Journal of the American Statistical Association,1970,65:1350-1361. [2] YIU C F,POON W Y.Estimating the polychoric correlation from misclassified data[J].British Journal of Mathematical and Statistical Psychology,2008,61:133-161. [3] TANG M L,QIU S F,POON W Y,et al.Test procedures for disease prevalence with partially validated data[J].Journal of Biopharmaceutical Statistics,2012,22:368-386. [4] BOESE D H,YOUNG D M,STAMEY J D.Confidence intervals for a binomial parameter based on binary data subject to false-positive misclassification[J].Computational Statatistics and Data Analysis,2006,50:3369-3385. [5] MORVAN J,COSTE J,ROUX C H,et al.Guillemin F.Prevalence in two-phase surveys:accuracy of screening procedure and corrected estimates[J].Annuals of Epidemiology,2008,18:261-269. [6] TANG M L,QIU S F,POON W Y.Confidence interval construction for disease prevalence based on partial validation series[J].Computational Statistics and Data Analysis,2012,56:1200-1220. [7] QIU S F,POON W Y,TANG M L.Sample size determination for disease prevalence studies with partially validated data[J].Statistical Methods in Medical Research,2016,25(1):37-63. [8] TANG M L,QIU S F,POON W Y.Comparison of disease prevalence in two populations in presence of misclassification[J].Biometrical Journal,2012,54(6):786-807. [9] QIU S F,POON W Y,TANG M L.Confidence intervals for proportion difference from two independent partially validated series[J].Statistical Methods in Medical Research,2016,25(5):2250-2273. [10] NEDELMAN J.The prevalence of malaria in Garki,Nideria:double sampling with a fallible expert[J].Biometrics,1988,44(3):635-655. [11] QIU S F,LIAN H,ZOU G Y,et al.Interval estimation for a proportion using a double sampling scheme with two fallible classifiers[J].Statistical Methods in Medical Research,2016.DOI:10.1177/0962280216681599. [12] LIU R T,HEUCH I,IRGENS L M.Maximum likelihood estimation of the proportion of congenital malformation using double registration systems[J].Biometrics,1994,50:433-444. 附錄 Score檢驗統計量的有關推導: 在模型1下, Fisher信息矩陣中各元素分別為: Fisher信息矩陣的逆矩陣中第一個對角元素為: 在模型2下,Fisher信息矩陣中各元素分別為: Fisher信息矩陣的逆矩陣中第1個對角元素為:2 模型與參數估計

2.1 模型1及其參數估計

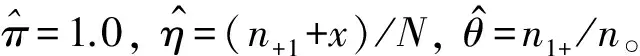
2.2 模型2及其參數估計

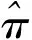
3 樣本量的確定
3.1 基于Wald置信區間的樣本量
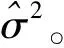
3.2 基于限制性極大似然估計下方差的Wald置信區間、似然比置信區間和Score置信區間的樣本量
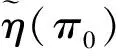
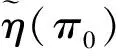
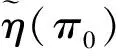
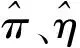
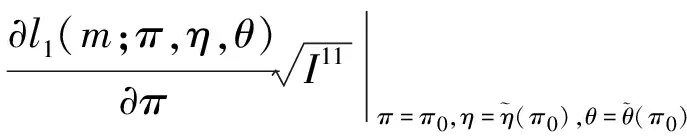
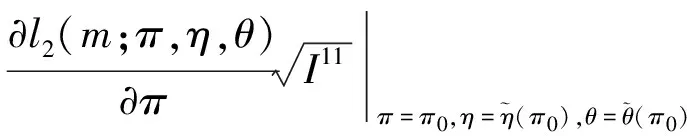
4 模擬研究
5 實例分析
6 討論

