基于維基百科的短文本相關度計算

荊 琪,段利國,李愛萍,2,趙 謙

(1.太原理工大學 計算機科學與技術學院,太原 030600; 2.武漢大學 軟件工程國家重點實驗室,武漢 430072)

0 概述

語義相關度計算作為自然語言處理領域一項基本性的研究工作,廣泛地應用于查詢擴展、詞義消歧、機器翻譯、知識抽取、自動糾錯等領域[1]。隨著社交媒體的出現,例如BBS、貼吧、聊天工具等,文本已成為重要的信息載體,其規模呈現出爆炸式的增長趨勢,尤其是短文本,作為一種新興的文本信息源,已成為了人們交流以及表達的重要形式。

目前,對于中文語義相關度的計算方法大多以相似度計算為基礎,然而相似度并不能完全替代相關度,相似度指的是“相像、相類”,具有可替代性;相關度反映的是“互相涉及、彼此關聯”,通常高頻出現在同一語境中的共現詞相關度較高,即相關性具有不可替換性。可以把相似性當作相關性計算的一個特征因子,作為最終結果的一部分。

由于短文本所表達的信息有限,因此需要大量的背景知識來對樣本特征進行擴展,獲取背景知識的方法可以分為2類:一類是基于語義詞典,如WordNet、Hownet等;另一類是對大規模語料庫進行統計分析來獲取背景知識。

維基百科是目前世界上最大的、多語種的、開放式的在線百科全書。目前含有35萬條中文條目,這些條目之間相互鏈接構成了一個巨大的語義網絡,很多研究者都青睞于利用維基百科來計算語義相關性。文獻[2]將基于Wordnet的一些經典算法用到維基百科的分類圖中,證明了維基百科在相關度計算中的可行性。文獻[3]提出了利用維基百科解釋文檔來計算兩個純文本之間的相關度,該算法被稱為明確語義分析(Explicit Semantic Analysis,ESA),但是該方法沒有考慮短文本的結構信息。文獻[4]通過從維基百科中收集突出的概念以及概念的解釋文檔,對ESA方法進行改進,提出了突出語義分析(Salient Semantic Analysis,SSA)方法,但該方法的缺點在于構建語義空間的過程中,不斷稀釋原文本的語義信息,因此在短文本相關度計算方面具有局限性。

隨著維基百科的普及和盛行,近年來越來越多的學者投入到中文維基百科的研究中。文獻[5-6]利用維基百科文檔間的鏈接結構提取了近40萬對語義相關詞,并計算了語義相關度。但該方法沒有考慮到維基百科類別信息。文獻[7-8]采用倒排索引進行加權,通過兩向量間的余弦夾角計算兩個詞語的語義相關度。文獻[9]利用類別信息擴展文本特征,進而對文本之間的相關度進行計算。文獻[10-11]采用統計規律和類別信息相結合的方式,通過構建概念集合的方式擴展短文本向量的信息,從而實現短文本之間的相關度計算。這些方法都只對維基百科的結構進行直接利用,并沒有深入挖掘維基百科中的語義信息以及結構信息,也沒有考慮短文本中詞語權重的問題。

本文將維基百科作為外部語義知識庫,利用維基百科的結構特征,如維基百科的分類體系結構、摘要中的鏈接結構、正文中的鏈接結構以及重定向消歧頁等,提出類別相關度與鏈接相關度相結合的詞語相關度計算方法。在此基礎上,提出基于詞形結構、詞序結構以及主題詞權重的句子相關度計算方法。

1 基于維基百科的詞語相關度計算

維基百科具有多樣的數據結構。圖1展示了一個基本的維基百科文檔頁面,并對本文所用到的鏈接結構、重定向、消歧頁、摘要、類別等信息進行說明。

1.1 類別相關度

維基百科中的每個條目對應于網站上的一個頁面,每個條目都歸屬于一個或多個類別。例如:“實驗”所屬的類別為“化學”和“物理”。維基百科提供了類別索引這一工具來組織和表達文檔之間的層次以及類別結構,除了根結點之外,其余的每個條目都可以在維基百科中找到其相應的位置。維基百科的層次分類結構如圖2所示。

傳統的語義相關度計算方法使用的是分類圖最短路徑方法,該方法首先將兩個詞匹配到一個語義網絡的概念結點,然后利用概念結點在分類圖上的路徑信息實現相關度計算[12]。對于待比較的兩個詞wa和wb,在分類圖中查找兩詞語的最小公共父類los,計算兩個詞語到最小公共父類的距離len(a)、len(b),距離越遠,相關關聯越小。兩個詞語的相關度計算為:

loga(len(wa)+len(wb))

(1)

其中,len(a)、len(b)分別表示詞語wa、wb到最小公共父類的距離。

利用數據結構的知識,可以把維基百科的層次分類圖轉化為樹狀結構。在樹狀結構中,需要考慮詞語類別的深度信息,深度信息可以說明它在維基百科分類體系中的地位。在以上公式的基礎上加入深度信息可以得到如下公式:

Simdca(wa,wb)=Simca(wa,wb)×

(2)

其中,depth(wa)表示詞語wa在維基百科分類樹中的深度。

1.2 鏈接相關度

維基百科中每個條目的解釋文檔中還含有豐富的鏈接信息,除了普通的解釋條目外,維基百科還含有多種引導性的條目,例如重定向條目和消歧義條目,利用這些鏈接可以有效計算兩個詞條的相關度。維基百科的鏈接結構如圖3所示。

圖3 維基百科鏈接結構示意圖

1.2.1 鏈接的重定向

維基百科向用戶提供了命名重定向功能,如果兩個條目的相關度達到一定程度,就將它們合并到同一個條目中,避免同一個事物有多個不同的條目。絕大多數情況下,維基百科重定向是對完全同一種事物的2種說法,例如周樹人與魯迅。少數情況下是將2個關聯性很強的條目放在一起,例如病態矩陣與條件數。所以,對于待比較的兩個詞語wa、wb,首先在維基百科的重定向列表中查找,若兩個詞互為重定向詞或者含有相同的重定向詞,則認為相關性為1;否則,查找各自的重定向詞,用其代替該詞參與之后的計算;若兩詞無重定向詞,則跳過此步。

1.2.2 鏈接的向量構建

根據維基百科解釋頁面的特點:每個頁面的首段為概念的摘要,所以出現在摘要中的詞語更能表達該條目的含義,帶有更強的語義信息,應該賦予更高的權重。維基百科中鏈接詞的數目過于繁多,構建出的向量維度過大,計算出的相關度過小。因此對摘要和全文分別計算其鏈接相關度,并賦予相應的權重。

對于詞w可以構建它的摘要、文檔鏈接向量:

Abstractw=[ (w1,fa(w1)),(w2,fa(w2)),…,

(wi,fa(wi)),…,(wn,fa(wn))]

(3)

Textw=[ (w1,ft(w1)),…,(w2,ft(w2)),…,

(wi,ft(wi)),…,(wn,ft(wn))]

(4)

其中,wi表示出現在摘要、文檔中的鏈接條目,fa(wi)表示wi這一條目在摘要中出現的頻率,ft(wi)表示wi這一條目在該概念文檔里出現的頻率。

1.2.3 鏈接的相關度計算

對于兩個詞語之間的摘要鏈接相關度,用向量之間的內積來表示:

(5)

其中,m、n分別代表詞語wa、wb摘要中鏈接條目的數目。

對于兩個解釋文檔的鏈接向量,由于概念文檔所含的條目過于繁多,因此頻率值過小,對它進行開方運算以達到放大頻率的目的,使得求得的相關度不會接近于0。利用向量之間的夾角余弦值計算,如式(6)所示。

(6)

其中,m、n分別代表詞語wa、wb的解釋文檔中鏈接條目的數目。

因此,兩詞語之間的鏈接相關度可以表示為:

simlinks(wa,wb)=α×simabstract+β×simtext

(7)

其中,α、β表示權重調節因子,且α+β=1。經實驗,當α=0.6,β=0.4時結果最優。

1.3 兩者結合的相關度計算

綜合類別相關度和鏈接結構的相關度計算,利用式(2)可以獲得維基百科的深度加權類別相關度,利用式(7)可以獲得兩個詞語基于鏈接結構的鏈接相關度計算,所以詞語wa與wb之間的綜合相關度為:

sim(wa,wb)=α×simdca+β×simlinks

(8)

其中,α、β表示權重調節因子,且α+β=1。經實驗,當α=0.75,β=0.25時結果最優。

2 基于維基百科的短文本相關度計算

2.1 詞形相關度

詞形相關度主要依賴于兩個短文本的共現詞語的頻率,即兩個待比較的文本經過預處理之后,共現詞語的頻率越高,相關度越大。在計算頻率時,用出現相同詞語的最少次數來計算,詞形相關度可用式(9)計算。

(9)

其中,same(A,B)表示兩個短文本中相同詞語的次數,而count(X)表示短文本X包含的詞語個數(包含相同詞語)。

2.2 詞序相關度

在對短文本語義相關度研究中,需要考慮詞序,例如:“青蛙吃昆蟲”與“昆蟲吃青蛙”兩句話的詞形相似度為1,而語義相似度并不一致。在相關度計算中,詞序可以作為一個權重較弱的特征來考慮。短文本的詞序主要表現為同一詞語在各短文本中序號不同,設same(A,B)為在短文本A和B中共現且只出現一次的詞語集合,對短文本A中的詞語依次進行編號,按照此編號來形成短文本B的詞序向量,進而得到該向量所構成的自然數的逆序數,代表兩個短文本中詞語順序不同的個數,逆序數越大,詞序相似度越低。因此,詞序相似度可用式(10)計算。

(10)

其中,Inverse(A,B)表示短文本B相對于A的逆序數,|same(A,B)||same(A,B)-1|為逆序數最大值的2倍。

2.3 基于詞對的語義相關度

短文本在語義上的相關度依賴于詞對之間的關聯,除了考慮短文本詞形、詞序的結構特點,還需考慮短文本的深層語義信息,并且語義相關度占有較大比重。傳統的短文本相關度計算方法是通過對各詞對的相關度求平均值來獲取的,為了突出更強的語義信息,本文選取兩個詞對中相關度最高的詞對計算。

1)詞對相關度矩陣構建

對于待比較的兩個短文本A、B,首先經過詞形標注等預處理,提取出具有實際意義的名詞。在構建矩陣之前,首先得到兩個短文本的特征詞集合向量A={a1,a2,…,an},B={b1,b2,…,bm},通過兩向量的笛卡爾積計算兩詞語的相關度,構建的兩個向量詞對相關度矩陣如下:

(11)

其中,sij表示短文本A中的第i個特征詞與短文本B中第j個特征詞之間的相關度。

2)最大匹配組合選擇

本文算法從相關度矩陣M中由大到小地選取min(m,n)個詞語組合的相關度值,要求每個詞語只出現一次,即在另一短文本中找到與其互為相關度最大的詞。選取的規則為:選擇矩陣中相關度最高的詞aij,即兩個短文本中相關度最高的詞語對,去掉第i行第j列,形成一個(m-1)×(n-1)的矩陣,將該矩陣作為待選擇的矩陣,重復以上步驟直到矩陣為空。經過選擇后,設最大序列為maxL={a23,a12,a3i,…,am1}。將平均值作為兩個短文本之間的相關度,公式為:

(12)

結合詞形詞序的計算公式,可以得出短文本相關度的計算公式:

Sim(A,B)=α×Simsa(A,B)+β×Siminv(A,B)+

γ×Simword(A,B)

(13)

其中,α+β+γ=1。經實驗,當α=0.25,β=0.15,γ=0.6時結果最優。

2.4 基于聚類的相關度計算方法

基于詞對的相關度比較的是兩個短文本中特征詞之間的相關度,而在短文本中,由于每個特征詞在短文本中的結構不同,所表達的信息強度也不同,因此每個特征詞在短文本中的重要性程度對短文本相關度計算也有很大影響。對待比較的短文本進行聚類,將相關度較高的聚為一類,利用這種方法可以更好地表達短文本的語義信息。聚類的算法如圖4所示。

圖4 文本間聚類的過程

短文本經過聚類得到組塊,每個組內詞語之間的相關度較高,實驗認為在一個組內的詞語數量越多,所表達的語義信息也更強烈,因此也更能代表整個短文本的含義,應該賦以更高的權重,計算權重的公式為:

(14)

其中,Count(Ai)表示詞語ai所在的組中詞語的個數,m表示短文本A中的詞語個數。聚類相關度計算公式如式(15)所示。

(15)

其中,Sim(ai,bj)表示短文本A中第i個詞語與短文本B中第j個詞語的相關度,計算公式為1.3節中的式(8)。

2.5 短文本相關度計算

綜合以上計算短文本的相關度方法,得到短文本相關度計算步驟如圖5所示。首先對短文本進行預處理,完成詞形相關度、詞序相關度的計算方法;其次通過詞對相關度矩陣的構建,完成基于詞對的語義相關度計算,綜合3種方法可得到短文本相關度;最后利用聚類方法對主題詞進行加權,得到聚類相關度。

圖5 短文本相關度計算步驟

3 實驗設置與結果分析

3.1 維基百科數據預處理及測試集

維基百科作為最大的百科知識全書,包含有一些特殊的語義結構,例如重定向、消歧頁面、導航(分類索引、特色內容、新聞動態、最近更改、隨機頁面)、幫助、工具等其他服務。本文所運用到的語言信息包括:詞語解釋文檔及文檔之間的鏈接信息和分類數據,重定向頁面和消歧頁面來處理同義詞和多義詞。

關于詞語相關度計算的測試集選用了人工翻譯WordSimilarity-353測試集[13-14]以及國防科學技術大學所統計的Words-240[15-16]。短文本相關度的測試集選擇中國數據庫萬維網知識提取大賽所提供的短文本語義相關度比賽評測數據集。

3.2 實驗結果分析

本實驗首先實現的是詞語的語義相關度計算,將各種方法計算所得的詞對相關度與人工標注的從高到低排列,隨機選取的部分詞對經過實驗得到的結果如圖6所示。

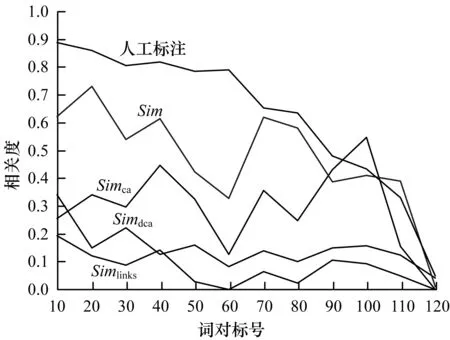
圖6 部分詞語相關度計算結果

經過實驗結果分析,可以得出這4種方法在計算詞語相關度時都有一定的合理性,但是Simdca作為一種Simca的改進算法,結果并沒有比Simca更好,原因在于Simdca加入了深度這一不穩定因素,對于同一深度差的詞對相關度計算并不明顯,Simlinks的結果基本都比較小,不超過0.2,因為維基百科中每個概念的解釋頁面包含太多的鏈接信息,兩個詞的公共鏈接所占的比率會比較低,相關度會比較小。結合表1各個算法所求得的Spearman相關系數可以看出Sim方法求得的相關系數最高,并且在0.7以上,與人工標注的更接近,實驗結果最為理想。其中,*表示相關性在 0.05 層上顯著(雙尾),**表示相關性在 0.01 層上顯著(雙尾)。

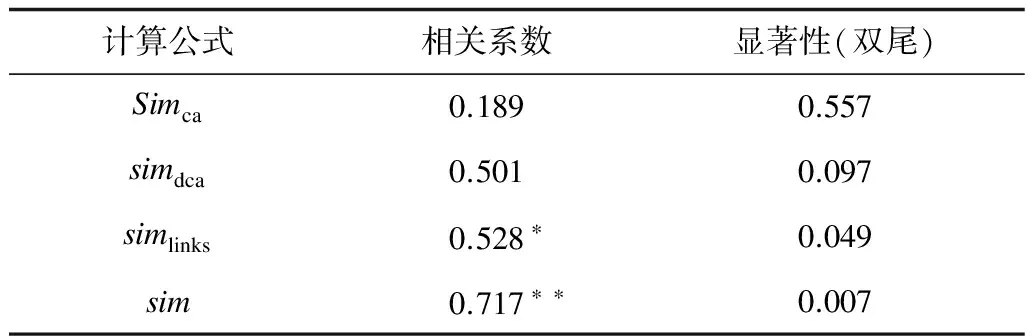
表1 Spearman相關系數

在實現詞語間語義相關度計算的基礎上,完成了對句子間相關度的計算。由于測試集的測試標準分為4個等級,并沒有給出具體的相關度數值,因此也將實驗的計算結果劃分為4個等級(相關度為0～0.25對應測試集中的0;0.25～0.5對應測試集中的1;0.5～0.75對應測試集中的2;0.75～1.0對應測試集中的3)。 隨機抽取的計算結果如表2所示,準確率的計算結果如圖7所示。

圖7 準確率比較

從結果中可以看出基于詞形詞序的準確率較低,因為這2種方法沒有考慮語義的信息,只考慮了句子的表征信息,基于詞序的方法準確率最低,因為詞序在相關度計算中僅起次要作用,詞序不同的情況下兩個短文本的相關度有可能很高,所以準確率最低。而其余的3種方法由于考慮到語義這一層面,取得了較好結果,準確率均在50%以上。但使用聚類并沒有提高準確率,究其原因在于測試集中短文本中可聚類的詞語并不很多,沒有達到提高句子主題詞權重的目的。

4 結束語

本文在目前基于維基百科的語義計算的基礎上,采用維基百科的類別與鏈接結構特征提出了一種計算詞語間相關度的方法,該方法利用摘要以及全文的鏈接相關度,極大地提高了結果的準確性。在計算出詞語相關度的基礎上,結合詞形詞序,并且根據文本間的聚類來對句子關鍵詞賦予較高權重,實現了句子間相關度計算的方法。實驗結果顯示,與人工判斷的結果相比較的Spearman相關系數,比傳統算法高出了很多,短文本間相關度的準確率也提高了不少。證明了該方法是可行和有效的。

該方法還有很多需要進一步探討和研究的地方,例如:由于聚類的算法需要額外進行詞語間的距離以及計算詞語間的相關度,因此時間復雜度較高。如何提高該方法的時間效率將是下一步研究的問題之一。

[1] 張紅春.中文維基百科的結構化信息抽取及詞語相關度計算[D].武漢:華中師范大學,2011.

[2] STRUBE M,PONZETTO S.Wiki Related Computing Semantic Relatedness Using Wikipedia[C]//Proceedings of the 21st National Conference on Artificial Intelligence.New York,USA:ACM Press,2006:1419-1424.

[3] GABRILOVICH G,MARKOVITCH S.Computing Semantic Relatedness Using Wikipedia-based Explict Semantic Analysis[C]//Proceedings of the 20th International Joint Conference on Artificial Intelligence.Berlin,Germany:Springer,2007:1606-1611.

[4] HASSAN S,MIHALCEA R.Semantic Relateness Using Salient Semantic Analysis[C]//Proceedings of the 25th AAAI Conference on Artificial Intelligence.[S.l.]:AAAI Press,2011:884-889.

[5] 李 赟.基于中文維基百科的語義知識挖掘相關研究[D].北京:北京郵電大學,2009.

[6] 李 赟,黃開妍,任福繼,等.維基百科的中文語義相關詞獲取及相關度分析計算[J].北京郵電大學學報,2009,32(3):109-112.

[7] 劉 軍,姚天昉.基于Wikipedia的語義相關度計算[J].計算機工程,2010,36(19):42-46.

[8] 涂新輝,張紅春,周琨峰,等.中文維基百科的結構化信息抽取及詞語相關度計算方法[J].中文信息學報,2012,26(3):109-115.

[9] 王 錦,王會珍,張 俐.基于維基百科類別的文本特征表示[J].中文信息學報,2011,25(2):27-31.

[10] 范云杰,劉懷亮.基于維基百科的中文短文本分類研究[J].現代圖書情報技術,2012,28(3):47-52.

[11] 汪 祥,賈 焰,周 斌,等.基于中文維基百科鏈接結構與分類體系的語義相關度計算[J].小型微型計算機系統,2011,32(11):2237-2242.

[12] 諶志群,高 飛,曾智軍.基于中文維基百科的詞語相關度計算[J].情報學報,2012,31(12):1265-1270.

[13] FINKELSTEIN L,GABRILOVICH E,MATIAS Y,et al.Placing Search in Context:The Concept Revisited[J].ACM Transactions on Information Systems,2002,20(1):116-131.

[14] 夏 天.中文信息處理中的相似度計算研究與應用[D].北京:北京理工大學,2005.

[15] 孫琛琛,申德榮,單 菁,等.WSR:一種基于維基百科結構信息的語義關聯度計算算法[J].計算機學報,2012,35(11):2361-2370.

[16] 伍 賽,楊冬青,韓近強.一種基于單詞相關度的文檔聚類新方法[J].計算機科學,2004,31(10):261-263.