關于二次函數綜合題的探究與思考

程艷

[摘? 要] 以二次函數為背景的綜合題，一般借助函數圖像上點的坐標建立與幾何圖形、圖形運動的關系，使問題形式多樣化. 掌握學習方法，參透函數知識，總結解題策略是突破綜合題的關鍵，本文以一道二次函數綜合題為例，進行解題探析.

[關鍵詞] 二次函數;綜合題;數形結合;平移;幾何;策略

問題背景解讀

二次函數是一次函數與反比例函數的延伸學習，也是代數與幾何相結合的代表性內容，對于該內容的學習從兩個方面進行：一是函數表達式，二是函數的圖像. 二次函數的表達式可以視為二元二次方程，求解函數參數的過程可以視為是解方程組的過程;而二次函數的圖像具有自身的特性，如開口方向和單調性，并且其性質與函數的參數有著直接的關系，也是初中階段研究的重點.

中考對于二次函數的考查通常以綜合題的形式進行，并且緊抓其幾何與代數的相融性，以直角坐標系為載體，借助點的坐標構建兩大知識領域的聯系. 近幾年的中考二次函數綜合題涉及的幾何圖形有三角形、圓、矩形、菱形、平行四邊形等，融合了平移、旋轉、翻折等內容，考查坐標求值、線段比例、面積構建、圖形構造等問題，對其進行深入探究具有十分重要的意義.

考題解例示范

二次函數綜合題的復雜不僅在于其計算過程的復雜，更在于解題的分析過程，以涉及平移并結合幾何圖形的二次函數題為例，需要把握函數解析式與圖形之間的坐標聯系，緊抓平移特性開展解題探索，下面對2018年上海市的二次函數壓軸題進行分析.

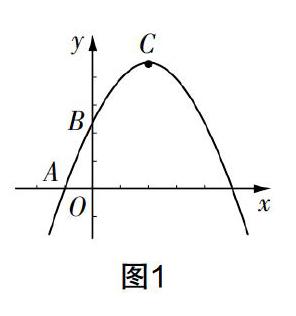
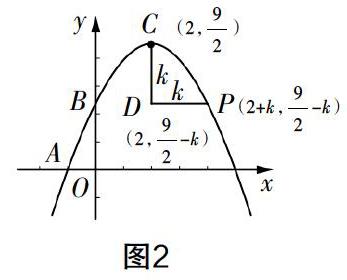
（2018年上海市中考卷第24題）如圖1所示，在平面直角坐標系中，拋物線y= -1/2x²+bx+c經過點A（-1，0）與B（0，5/2），點C是拋物線的頂點，點D在拋物線的對稱軸上且位于點C的下方，將線段CD繞點D順時針旋轉90°，點C正好落在拋物線的點P處.

（1）求拋物線的表達式;

（2）求線段CD的長;

（3）將拋物線平移，使得點C與原點O相重合，此時點P落在點E處，點M落在y軸上，如果以四點O，M，E，D為頂點的四邊形面積為8，試求點M的坐標.

破題第一招——細致讀題，標畫提煉

一般函數壓軸題的題干文字敘述較多，關鍵的條件均隱含在其中，因此在讀題時需要放平心態，集中注意力. 讀題可以分兩步進行：第一步是全題通讀，標注其中的關鍵詞語;第二步是條件提煉，即關注題干描述函數圖像的詞語，從中提煉拋物線的特征，如開口方向、頂點坐標和對稱軸等，通過這樣的細致讀題來構建二次函數的框架.

破題第二招——構建模型，理清思路

求解二次函數最為有效的方法是構建特定的模型，問題的分析應建立在具體模型上. 如求解二次函數的表達式應根據待定系數法，構建“點坐標——方程組——函數參數”的模型;求解線段長應把握幾何與代數的聯系性，構建“幾何性質——點坐標——線段長”的模型，或者基于方程思想構建求解幾何線段的函數方程;而求解圖形面積問題時，則需要構建研究圖形的面積模型，將問題轉化為求解關鍵點的坐標.

破題第三招——有理有據，有序全面

數學解題過程講求“有理有據，有序全面”八字原則，“有理有據”即分析時必須依據基本的數學原理和性質，所進行的推導必須在教材中有出處，尤其是解函數綜合題，對題干條件進行轉化時都必須有依據. 而“有序全面”則指的是在對問題進行拆解、結論推演時必須按照一定的次序，遵循一定的邏輯，并且問題分析要全面，做到不遺漏不重復. 這與命題的過程和原則是一致的，必要時可以采用分類討論的方法，確保所獲得的答案全面準確.

考題解后思考

上述考題以旋轉、平移作為載體，主要考查了二次函數表達式、平移性質、求解線段長和幾何面積模型等內容. 從解題過程的思想方法來看，考查了方程思想、數形結合思想，理順幾何與函數之間的聯系是突破考題的關鍵，下面進一步反思解題，總結學習經驗.

1. 透視函數知識，數形角度思考

二次函數知識是初中數學的重難點知識，其幾何與代數的雙重性質往往是中考壓軸題的命題素材，對于二次函數知識應該從幾何與代數兩個視角進行概念、性質透視. 如對于二次函數的表達式學習應結合代數的多元方程，而對于函數性質特征的學習則需要結合對應的圖像，可根據圖像的變化理解二次函數的頂點坐標、開口方向、單調性和最值. 同時，對于二次函數的學習還需要進行數形對照，如結合圖像理解參數a的大小和符號，根據圖像理解頂點坐標與對稱軸的關系等. 二次函數學習的關鍵是建立一個完善的研究體系，然后采用合理的方法透視內容.

2. 緊抓知識聯系，構建分析策略

二次函數綜合題是中考的重點題型，上述題目將平面幾何、圖形運動相結合只是其中較為常見的形式，求解這類綜合問題的關鍵是抓住知識之間的紐帶，從知識聯系性角度突破. 如函數與平移、旋轉問題則需要結合圖形運動的不變性，從動態問題中提煉不變條件和變化規律，建立函數運動的模型，探究點運動的規律;而對于函數與幾何圖形結合問題，則應基于數形結合研究方法，依據“圖像←→特征←→線段←→點坐標←→函數表達式”的解題策略進行單向或多向探究，充分利用“點坐標”的銜接作用對問題進行轉化. 對于函數中的幾何問題，可以結合點坐標，基于方程思想構建研究模型，通過解方程的方式實現求解. 解決函數綜合題實際上就是策略運用和模型構建的過程，掌握解題策略即可顯著提升解題能力.

寫在最后

任何知識都不是孤立存在的，這也是函數綜合問題命制的背景，因此我們在學習二次函數知識時要將其放在整個知識體系中，把握二次函數的特性進行多視角的知識透視梳理，只有這樣才有利于后續的知識遷移、拓展學習，也有利于構建二次函數綜合題的解題策略.