一道基于鏡像法對電場的嚴格求解問題

黃志豪 張 雪,2 李 軒 張冠中

(1.東北師范大學物理學院,吉林 長春 130024;2.鄭州市第四十二中學,河南 鄭州 450000)

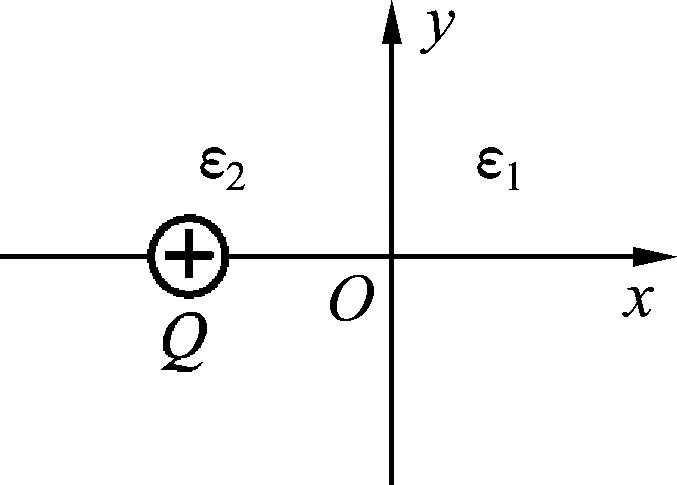
圖1

如圖1所示,x>0和x<0區域分別充滿電容率ε1和ε2的各向同性線性介質,x<0區域有一點電荷Q,它到分界面x=0的距離為d(d<0),求各區域的電場分布.

文獻[1]將上文作為例題促進學生對鏡像法一節的理解,隨后在解題步驟中根據唯一性定理設出“像點荷的大小為q′,位置x=-d”作為條件進行求解,這是典型的“嘗試法”解題思路.盡管最后結果正確,但由于解題過程不甚嚴格,導致部分學生對其理解存在困難,同時也不利于學生對鏡像法基本思想的準確把握,甚至有部分學生產生了“利用鏡像法求解場方程表達式一般不可準確求解”的錯誤思想.本文提出了一種嚴格求解的方法得到場方程表達式,并作出相互正交的等勢線和電場線簇圖形,討論了分界面兩側介質電容率之比對圖形的影響.

1 場問題的嚴格求解

記x>0區域電勢為φ1,x<0區域電勢為φ2.

定義

首先對x>0區域電勢分析,根據唯一性定理,可設像點荷為Q′(a,0,0)(a<0).則x>0空間任一點電勢可表示為

(1)

對于x<0區域電勢,同理可設像點荷電量為Q′(b,0,0)(b>0).則x<0空間任一點電勢可表示為

(2)

根據邊值關系,分界面x=0上有

φ1|x=0=φ2|x=0.

(3)

(4)

即

(5)

(6)

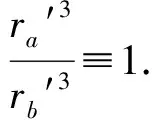
a=-b,Q′=-Q″.

(7)

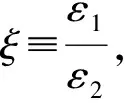
(8)

同理可得Q″=ηQ,Q′=-ηQ,a=-b=d,即

a=-b=d,ra=rd,ra′=rb′=rd′.

(9)

(10)

利用E=-φ得電場強度

(11)

(12)

式(11)所得結果和嘗試法所得結果完全一致,證明本文嚴格求解的方法是正確的.

2 電場線和等勢線簇圖形

為簡單起見,考慮到Q為固定值,則可將等勢線簇函數表示為

(13)

(14)

電場線簇函數為

(15)

(16)

研究ξ對z=0面等勢線和電場線簇圖形的影響,作出對應的等勢線和電場線簇圖形,如圖2所示.

設定參數:點電荷坐標Q(-1,0,0),介質電容率之比分別為ξ1=15、ξ2=5、ξ3=1、ξ4=0.05.

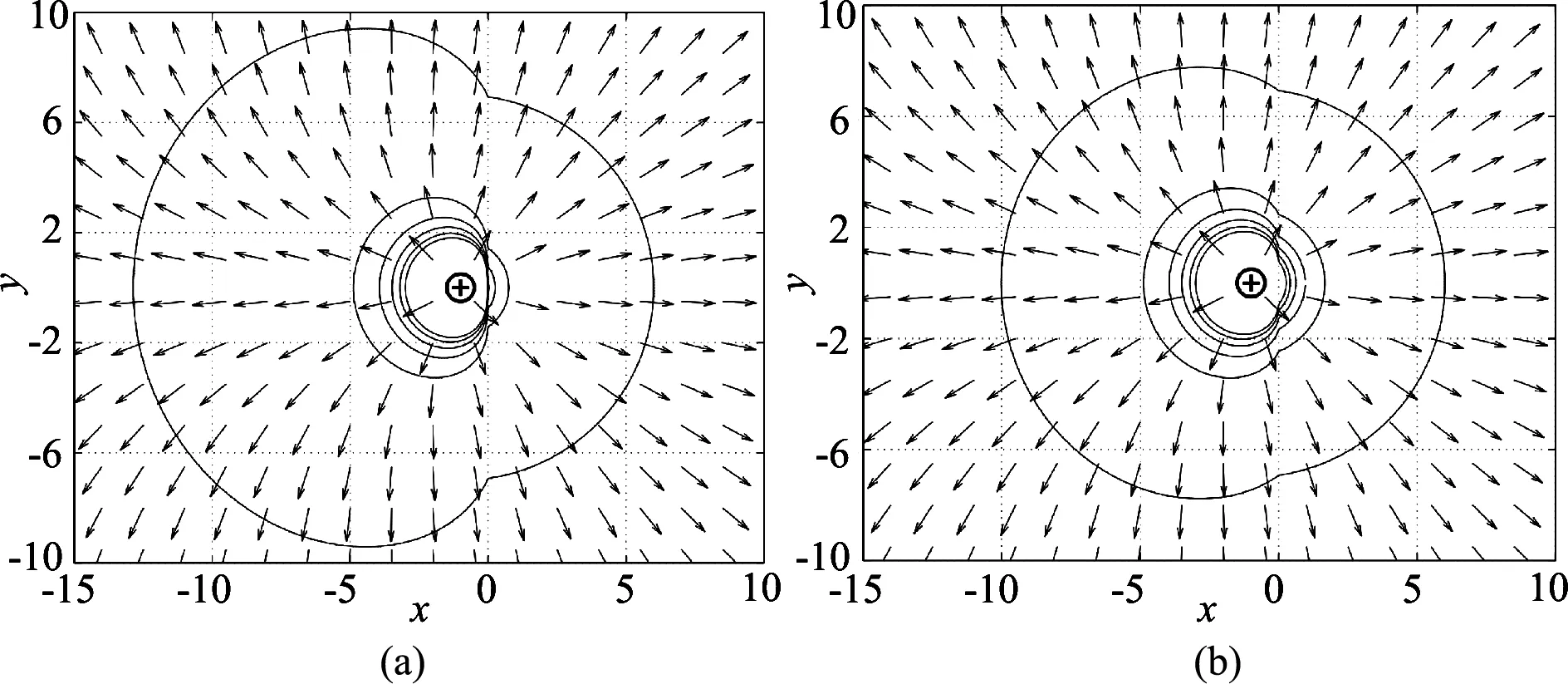
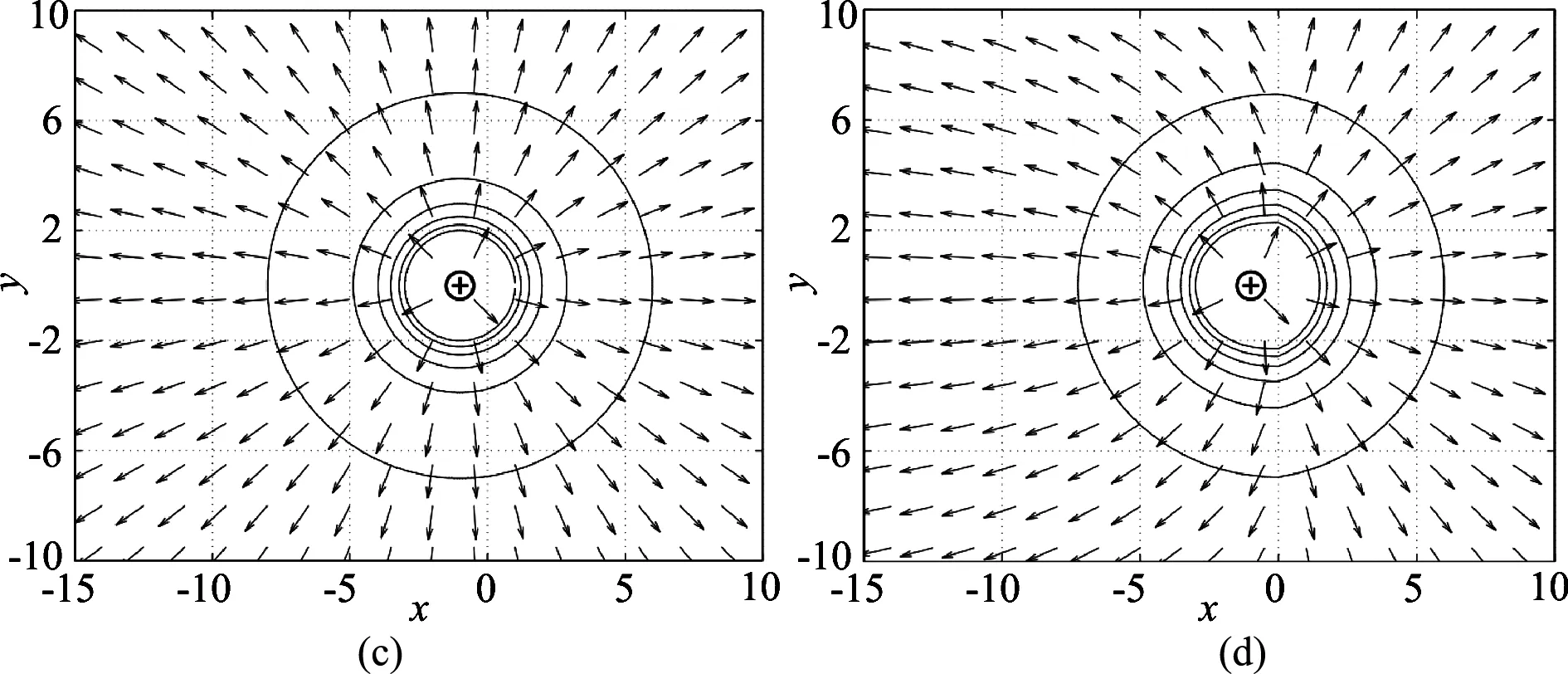
圖2 z=0平面不同ξ值下電勢電場正交簇圖形

(圖aξ1=15; 圖bξ2=5； 圖cξ3=1； 圖dξ4=0.05)

由圖可知,每處箭頭方向代表電場方向,……