牽引車動力總成懸置系統優化分析*

鄭利鋒 王鐵 張瑞亮

（太原理工大學，太原 030024）

1 前言

車輛舒適性主要受振動影響，引起車輛振動的主要振源有發動機工作振動激勵、路面隨機激勵及發動機以外旋轉部件的不平衡激勵。其中發動機作為激勵源對整車NVH性能和舒適性有較大影響。

本文針對某牽引車使用鋁殼代替鑄鐵殼變速器，動力總成升級后出現怠速工況振動較大問題，通過AD?AMS軟件對懸置系統剛體模態進行仿真分析，并結合模態測試分析驗證仿真模型的有效性。以懸置剛度為優化參數，懸置系統主振動能量分布的加權組合為優化目標，給出優化后懸置剛度參數。最后，在怠速工況下對轉向盤振動量和懸置傳遞率進行測試，分析并評價懸置系統優化后對整車振動性能的改善效果。

2 動力總成懸置系統分析

考慮到本文研究的牽引車動力總成通過四點平直橡膠懸置安裝到車架上，為了建立相應的理論分析模型，做了以下簡化假定：

a.動力總成相對平衡位置的位移較小，可認為動力總成的隨動坐標與整體坐標重合；

b.由于動力總成的剛度遠大于懸置剛度，動力總成簡化成剛體；

c.橡膠懸置在局部坐標下，考慮3個方向的平動剛度和阻尼，忽略旋轉剛度和阻尼；

d.動力總成慣性矩和慣性積不隨時間變化；

e.車架及底盤被看作剛體支撐。

2.1 建立動力總成運動方程

牽引車動力總成系統模型由發動機、離合器、變速器及附件組成，通過4個平置橡膠懸置連接到車架上，布置示意圖如圖1所示。坐標系Goxyz固定到動力總成的質心上并處于系統靜平衡位置。x軸平行于車輛前進方向，z軸垂直向上，y軸垂直于xy平面向左。橡膠懸置按照圖1所示進行布置。其中，1-4代表懸置布置位置。

圖1 動力總成懸置系統6自由度模型示意圖

基于假設和Lagrange原理，得到動力總成6自由度運動方程如下：

2.2 系統評價要求

動力總成懸置系統設計的優劣主要通過系統頻率是否匹配合理來進行評價。圖2為不同阻尼下放大系數隨頻率變化的曲線。懸置頻率匹配的目的是降低發動機振動向車架的傳遞，同時減少來自路面激勵向發動機的傳遞。為了獲得較好的發動機隔振效果，動力總成懸置系統的各階固有頻率一般不應高于發動機激勵頻率的倍。對本文研究的牽引車搭載六缸四沖程發動機，怠速轉速為600 r/min，發動機點火頻率為30 Hz，因此懸置系統的頻率不應高于21.2 Hz。為避開路面激勵的低頻振動，懸置系統固有頻率應大于路面激勵頻率的4/3倍。由于路面激勵頻率通常不超過3 Hz，因此要使懸置系統的固有頻率大于3 Hz/0.75（即4 Hz）。考慮到懸架和車身的固有頻率也在低頻范圍，接近5 Hz，因此，懸置系統的各階固有頻率一般設計在5~21.2 Hz之間。

3 動力總成懸置系統模態仿真分析

應用ADAMS軟件對動力總成懸置系統剛體模態進行仿真計算，并結合采用序列二次規劃法SQP（Sequen?tial Quadratic Programming）算法進行優化分析。

圖2 傳遞率隨頻率比變化曲線

3.1 建立動力總成6自由度計算模型

假定動力總成為剛體模型，輸入參數不隨時間變化；橡膠懸置通過Bushing單元模擬，只考慮3個平動方向的剛度和阻尼；車架為剛體模型。以下研究的牽引車動力總成通過4點平置、左右對稱橡膠懸置支撐，質量M和慣性參數Iij見表1，動力總成質心坐標和懸置位置坐標見表2。

表1 動力總成質量和慣性參數

表2 動力總成質心位置和懸置坐標

對于同一橡膠懸置軟墊，隨著頻率增加，其動剛度值相應增加，在低頻段動剛度隨頻率變化較快，在高頻段變化較平緩；振動動態幅值越大，動剛度越小；振動動態幅值越小，動剛度值越大[1]。一般來說，動剛度大于靜剛度，動靜比在1.2-3之間，有些可能會大于3，通過試驗測得靜剛度（Ku、Kv、Kw）及動剛度系數見表3。

表3 懸置元件參數

通過計算得到動力總成系統沿各方向的固有頻率和模態能量分布百分比如表4所示。從表4可以看出，系統固有頻率繞X軸的旋轉頻率最大，最大值28.5 Hz，超出目標值21.2 Hz，接近發動機的激勵頻率；模態能量相互耦合，解耦率普遍較低。因此認為懸置匹配不合理和模態耦合是引起整車怠速振動較大的主要原因。

表4 動力總成固有頻率和模態能量分布

3.2 模態測試

本文采用LMS公司的錘激法（Impact Testing）進行測試得到頻響函數（FRF），然后使用Modal Analysis模塊對得到的FRF數據進行分析處理，通過Polymax方法進行識別得到懸置系統的固有頻率及對應振型。為了更直觀查看動力總成6個自由度的振型，使用8個三向加速度傳感器成矩形布置在發動機缸體表面，見圖3。由于操作空間限制，考慮到發動機的激勵主要在Z向和繞X的旋轉，因此捶擊激勵施加在Z向和Y向，激勵點選擇在傳感器附近[2-3]。

由于懸置系統是搭載整車上進行測試而非臺架上，車架在這個區間也存在部分模態頻率，在模態數據分析過程中需要剔除車架振動的影響。消除干擾頻率后，測試得到系統固有頻率見表5，對應的振型見圖4。測試過程中，測試方案的激勵在X向的響應并不明顯，在數據分析中沒有識別到X向固有頻率和振型。從結果對比可以看出，計算結果與測試結果趨勢一致；Rx方向模態和測試結果比較接近，因此，使用該模型對懸置系統進行優化可行。

圖3 傳感器布置

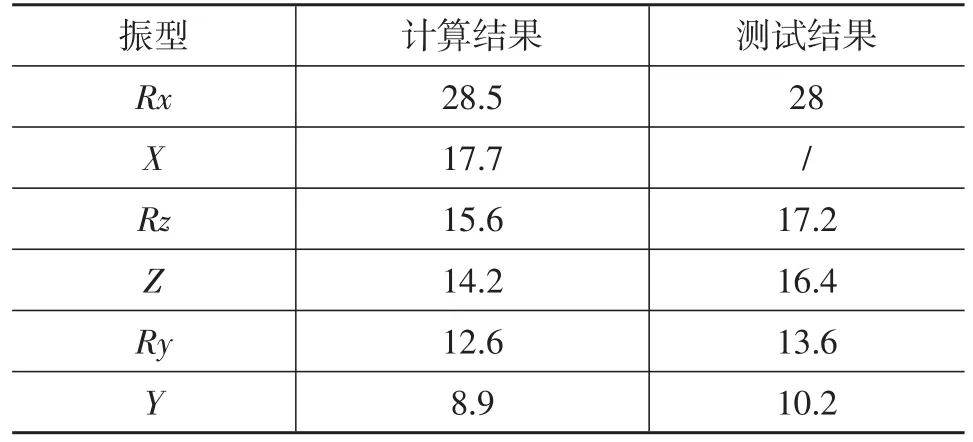
表5 計算結果和測試結果對比 Hz

3.3 系統優化分析

動力總成懸置系統優化一般通過選擇合適的懸置剛度、合理的懸置布置位置及合適的布置角度，使系統固有頻率遠離發動機激勵，同時降低各模態之間耦合程度，最終使發動機振動傳到車架上的振動達到最小。

a.優化變量設定

考慮到動力總成的安裝位置、布置空間的限制、成本及開發時間的限制，懸置系統近似成對稱布置，因此選取前、后懸置參數為優化參數。

圖4 固有頻率及振型

b.優化目標設定

基于能量理論，懸置系統作j階模態振動時，第k個廣義坐標的能量表示為：

以動力總成懸置系統主振動能量分布的某種組合作為優化設計的目標函數，如下：

c.約束條件設定

根據上述系統評價要求，系統在6個方向的固有頻率必須在5-21.2Hz之間。

d.優化分析

利用ADAMS的優化工具，采用序列二次規劃法SQP算法，以懸置系統振動能量解耦程度最大為優化目標，對其進行優化[4-5]，優化后懸置剛度參數見表6。

表6 優化后的懸置剛度參數

使用優化后的懸置剛度參數進行模態分析，得到系統的固有頻率和模態能量分布見表7。

從表7可以看出，繞X軸（Rx）的能量達到96.3%解耦率很高；模態能量分布在Z向和俯仰方向（Ry）存在耦合，但在Z方向的主振動能量達到66%，考慮到固有頻率遠離發動機激勵頻率，可以接受；其它方向模態解耦程度較高。系統各階模態的固有頻率均滿足頻率匹配要求（5-21.2 Hz）。總體來說，優化后的計算結果基本滿足設計要求。

表7 優化后的固有頻率和模態能量分布

4 整車性能測試評估

4.1 轉向盤的測試結果對比

為了更好的評估動力總成懸置系統優化前、后對整車性能的影響，在整車怠速下對轉向盤進行主觀評估和振動測試，測試布點在轉向盤回正后12點位置。

測試得到的動力總成懸置系統優化前、后轉向盤在怠速下振動加速度均方根值如圖5所示。從圖5可以看出，優化后加速度明顯降低，說明動力總成懸置系統優化可有效改善整車振動。

圖5 怠速工況下轉向盤優化前、后結果對比

4.2 優化前、后懸置傳遞率對比

為了評估懸置系統隔振性能，對優化前、后懸置點的振動傳遞率進行測試，如表8所示。從表8中可以看出，懸置參數優化后，傳遞率明顯降低，有效改善了發動機激勵向整車的傳遞。

5 結束語

針對某牽引車使用鋁殼代替鑄鐵殼變速器，動力總成升級后出現怠速工況振動較大問題，利用ADAMS軟件對懸置系統剛體模態進行了仿真分析，得到以下結論：

a.分析了引起整車怠速振動的原因，提出了優化方向；

b.通過模態試驗驗證了仿真模型的有效性，并給出了優化后的懸置參數；

c.在怠速工況下，通過對優化前、后轉向盤振動量和懸置傳遞率進行測試和主觀評估表明，優化后整車振動得到明顯改善。

表8 不同懸置位置的振動傳遞率

[1]劉祖斌,劉英杰.發動機懸置設計中的動、靜剛度參數研究.汽車技術,2008（6）：21-23.

[2]劉習軍,賈啟芬.工程振動理論與測試技術.北京：高等教育出版社,2006.

[3]張武,陳劍,陳鳴.汽車動力總成懸置系統多工況運行模態試驗研究.中國機械工程,2013（22）：3118-3123.

[4]陳大明,上官文斌.動力總成懸置系統剛體模態優化設計方法的研究.汽車技術,2011（2）：34-38.

[5]Boggs P.T.and Tolle J.W.Sequential Quadratic Programming.Acta Numerica 1996:1-52.