模態綜合法在航天器結構動力學分析中的應用研究

尹家聰，謝偉華，陳 曦，劉 波

(中國空間技術研究院通信衛星事業部，北京100094)

0 引言

部件模態綜合法(Component Mode Synthesis， CMS)又簡稱模態綜合法，起源于20世紀50年代初，最早用于計算飛機機翼及整機的固有振動問題。1960年起，Hurty首先確立了模態坐標、模態綜合等概念[1]，并逐步發展出以Craig-Bampton為代表的固定界面模態綜合法[2]和自由界面模態綜合法[3-5]，以及混合界面模態綜合法[6-7]等多種方法。Craig在2000年對模態綜合法的發展進行了詳細綜述[8]。

模態綜合法具有兩大優勢和一是可以大幅縮減結構自由度(縮減后的有限元模型稱為縮減模型或縮聚模型)，提高計算效率，節約計算成本；二是可以封裝產品設計的幾何和材料信息，保護企業知識產權。

本文將首先回顧模態綜合法在國內外航天器結構動力學分析中的應用現狀和模態綜合法的基本理論，然后重點研究模態綜合法在航天領域結構動力學分析應用中受限的兩個問題，即部組件有限元物理模型一級縮聚的接口匹配問題和縮聚/物理混合模型的二級縮聚問題。

1 模態綜合法在航天工業中的應用現狀

目前，模態綜合法已集成到各大結構動力學計算商業軟件中，并在航天工業領域得到了廣泛應用。例如，NASA在1990年采用MSC. Nastran軟件的超單元模態綜合分析功能，計算了國際空間站在軌多種動力載荷下的響應特性[9]；MIT在1999年利用詹姆斯韋伯空間望遠鏡(JWST)的模態綜合后的有限元縮聚模型(見圖1)，完成了結構-光學-控制一體化的集成建模模型，并進行了初步的微振動分析[10]；21世紀初，國外某公司研制的某衛星，其整星有限元模型也是采用模態綜合法進行建模(見圖2)，其中星本體采用有限元物理模型建模，而太陽翼、天線等則采用模態綜合法得到一級縮聚模型建模。(注：本文中，一級縮聚模型指采用模態綜合法，直接由有限元物理模型縮聚得到的模型；縮聚/物理混合模型指將多個一級縮聚模型分別與未縮聚的有限元物理模型裝配在一起的混合模型；二級縮聚指將縮聚/物理混合模型再次采用模態綜合法進行縮聚，從而把一級縮聚模型未縮減的界面自由度進一步縮減的過程。)

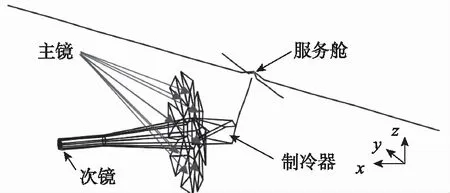
圖1 詹姆斯韋伯望遠鏡的有限元縮聚模型Fig.1 The reduced finite element model of JWST

圖2 某衛星有限元縮聚/物理混合模型Fig.2 A hybrid finite element model of a satellite contained both unreduced and reduced sub-structures

圖3 我國為巴基斯坦研制的通信衛星的有限元模型[18]Fig.3 The finite element model of a Pakistani telecommunication satellite made by China

我國航天工業部門在20世紀80年代已認識到模態綜合法的優勢[11]，模態綜合法在運載火箭的全箭建模[12]、航天器/火箭的器箭耦合載荷分析[13]、剛柔耦合及全柔性航天器動力學建模[14]，以及大型航天相機[15]、通信衛星[16]、空間站[17]結構動力學分析中均已得到應用。例如在我國在為巴基斯坦研制衛星過程中，在完成衛星動力學分析后，將衛星的有限元物理模型(見圖3)采用模態綜合法進行一級縮聚，提供給運載方開展耦合載荷分析，預示運載火箭發射過程中的衛星響應，并為衛星地面力學試驗條件制定提供參考依據。

總之，模態綜合法可以有效解決航天器研制過程中，部組件級、航天器系統級、航天器/運載器大系統級的結構耦合分析問題，但也有一些因素制約了模態綜合法在航天器結構動力學分析的工程實踐。航天器總體設計部門習慣采用傳統有限元物理模型開展動力學分析，模態綜合法在組件級、航天器系統級、航天器/火箭大系統級的動力學分析中的應用尚未形成系統，其應用帶來的流程變化成熟度也有待提高。

為了拓展模態綜合法的工程實踐，本文重點研究了模態綜合法在應用過程中的兩個限制性問題：

1)一級縮聚的接口匹配問題。一些航天器研制過程中，部組件有限元模型越建越細，自由度數目巨大，造成航天器系統結構動力學分析無法計算或計算效率低下，需采用模態綜合法對部組件模型進行一級縮聚，以便于航天器系統開展分析。然而，部分部組件模型的建模軟件與航天器系統不匹配，使得一級縮聚模型無法有效傳遞。為此，航天器總體設計部門應研究一級縮聚的接口匹配問題，從而解決和規范部組件縮聚模型的接口。

2)縮聚/物理混合模型的二級縮聚問題。一些航天器與運載的耦合載荷分析，僅針對航天器有限元物理模型的一級縮聚(見圖3)，但隨著航天器部組件一級縮聚模型的應用，航天器結構動力學分析必然會出現縮聚/物理混合的有限元模型(見圖2)。因此航天器總體設計部門應解決縮聚/物理混合模型的二級縮聚問題，從而解決和規范航天器系統和運載的縮聚模型接口。

本文通過Fortran/ Matlab混合編程和采用Nastran DMAP語言二次開發，在一級縮聚的接口匹配和縮聚/物理混合模型的二級縮聚問題上進行了探索，并在航天器型號研制過程中得到了初步應用。

2 模態綜合法原理

模態綜合法本質上是一種Rayleigh-Ritz降階方法，即通過把子結構的物理坐標x表示為幾種已知部件模態集的線性組合，實現從物理坐標空間到混合界面坐標空間的變換，并縮減子結構的自由度獲得縮聚模型。模態綜合法的基本原理可通過Majed等于2005年提出的一種剩余柔度混合界面模態綜合法(Residual Flexibility Mixed- Boundary Method，RFMB)[7]統一歸納如下：

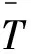
(1)

其中對應于各個模態集的廣義坐標用q表示，各模態集的具體計算方法詳見Craig的綜述[8]。

式(1)可進一步展開寫為：

xb=qC

(2a)

(2b)

(2c)

或矩陣形式:

(3)

其中q1表示廣義坐標空間。由式(2a)和(2b)可得:

(4)

記qN=qk，那么有q1=T2q2，即:

其中q2表示混合界面坐標空間。

由式(3)和式(5)可得RFMB方法從物理坐標空間到混合界面坐標空間的變換：

x=T1T2q2

(6)

或

(7)

其中，

(8)

(9)

3)另一種常用的混合界面模態綜合法(Modified Hintz’s Mixed-Boundary Method, MHMB)，是Hintz’s Mixed-Boundary Method (HMB)[6]的一個改進，其坐標變換可寫為:

(11)

該方法是Nastran軟件混合界面模態綜合法的默認算法[19]。

在工程應用中，一般根據實際需求選擇不同的模態綜合法：1) 固定界面模態綜合法的優點在于原理清晰，算法簡單，因此當主要目的在于縮聚子結構的自由度，而無需顯示子結構的振動形態時，使用固定界面模態綜合法將子結構與其他結構的連接面固支進行自由度縮聚，即可滿足工程需求；2) 自由界面模態綜合法的優點在于自由邊界的子結構模態試驗容易實現，模態綜合參數易于得到試驗驗證，因此當需要通過自由邊界模態試驗修正子結構建模結果時，可以采用自由界面模態綜合法；3) 混合界面模態綜合法的優點在于既可以充分縮減子結構的自由度，還可以通過輪廓顯示單元將縮聚后的固定界面和自由界面點連接起來，以顯示子結構的幾何輪廓及其在動力載荷下的振動響應，且無需經過數據恢復即可獲得自由界面點上的動力響應，縮聚后的模型特別適合于代替子結構的有限元物理模型用于不同設計部門間的模型傳遞。

3 有限元一級縮聚的接口匹配問題

早在1966年，為了滿足航空航天工業對結構分析的需求，NASA就主持開發了商業有限元軟件Nastran。經過半個多世紀的發展，Nastran已成為航天工業有限元分析的國際標準。我國各航天器總體部門也多采用Nastran進行航天器有限元建模和結構力學分析。然而，部分航天器部組件研制單位習慣采用ANSYS或其他非Nastran的有限元商業軟件進行力學分析；不同軟件在使用模態綜合法縮聚子結構模型時具有不同的格式，這為部組件一級縮聚模型向航天器系統級的傳遞帶來了困難。

以ANSYS軟件建立的部組件有限元模型為例，本文采用如下流程解決一級縮聚的接口匹配問題：1)用ANSYS的HBMAT命令輸出部組件模型，以Harwell-Boeing稀疏矩陣格式存儲的剛度和質量矩陣，以及結點坐標和自由度編號信息；2) 用Fortran軟件編程快速讀取ANSYS輸出的剛度、質量矩陣，并轉換為Matlab可以識別的三元組稀疏矩陣格式；3) 用Matlab讀取步驟1、2的輸出數據，并用Matlab編程實現Nastran的混合界面模態綜合法，生成可以被Nastran識別的一級縮聚模型，包括縮聚后的剛度、質量矩陣，界面自由度和廣義自由度的編號信息，界面點的坐標以及輪廓顯示單元的定義；4) 用Nastran軟件讀取一級縮聚模型，并完成其與航天器系統級有限元模型的裝配。

作為示例，圖4(a)設定了某衛星推進分系統的氣瓶ANSYS有限元模型。該模型采用體單元建模，在自由邊界條件下大約有5萬個結點，1.7萬個單元，15萬個自由度。通過自編的Fortran/Matlab混合界面模態綜合法程序，可以將此ANSYS有限元物理模型一級縮聚為Nastran可識別的縮聚模型，如圖4(b)所示。圖4(b)中，結點1、2的自由度設置為氣瓶在整星安裝的固定界面自由度；結點3～14的自由度設置為自由界面自由度。結點1～14通過24個PLOTEL輪廓單元組成氣瓶縮聚模型的顯示框架。縮聚后的模型僅有104個自由度(包括50個正交模態即k=50)，相對于原模型大幅減少了自由度。

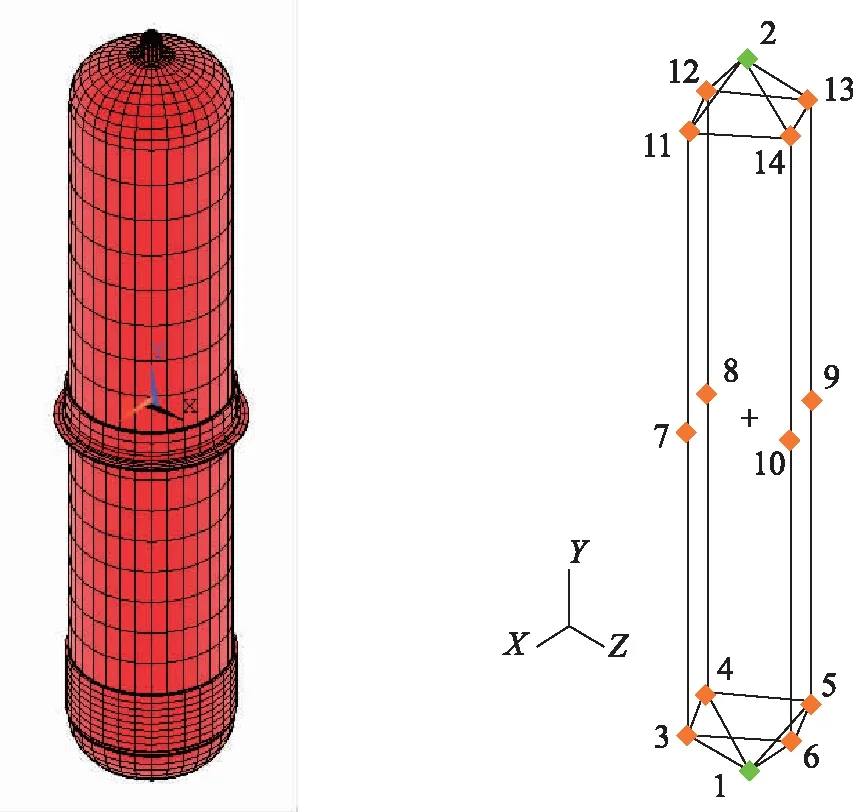
(a)縮聚前ANSYS模型 (b) 縮聚后Nastran模型圖4 某氣瓶縮聚前后的有限元模型Fig.4 The original ANSYS finite element model of a gas tank (left) and its reduced model in Nastran(right)

表1給出了某氣瓶縮聚前后自由邊界條件下的固有頻率對比結果：其中，前6階剛體頻率雖然由于計算誤差不完全為0，但計算結果相近，且縮聚前后前6階剛體模態在各個自由度方向的模態有效質量百分比之和均為100%。圖5給出了某氣瓶縮聚前后自由邊界下第7階固有頻率的模態振型。由表1和圖5可知：縮聚算法正確有效，氣瓶的Nastran縮聚模型可以用于航天器整體的有限元建模。

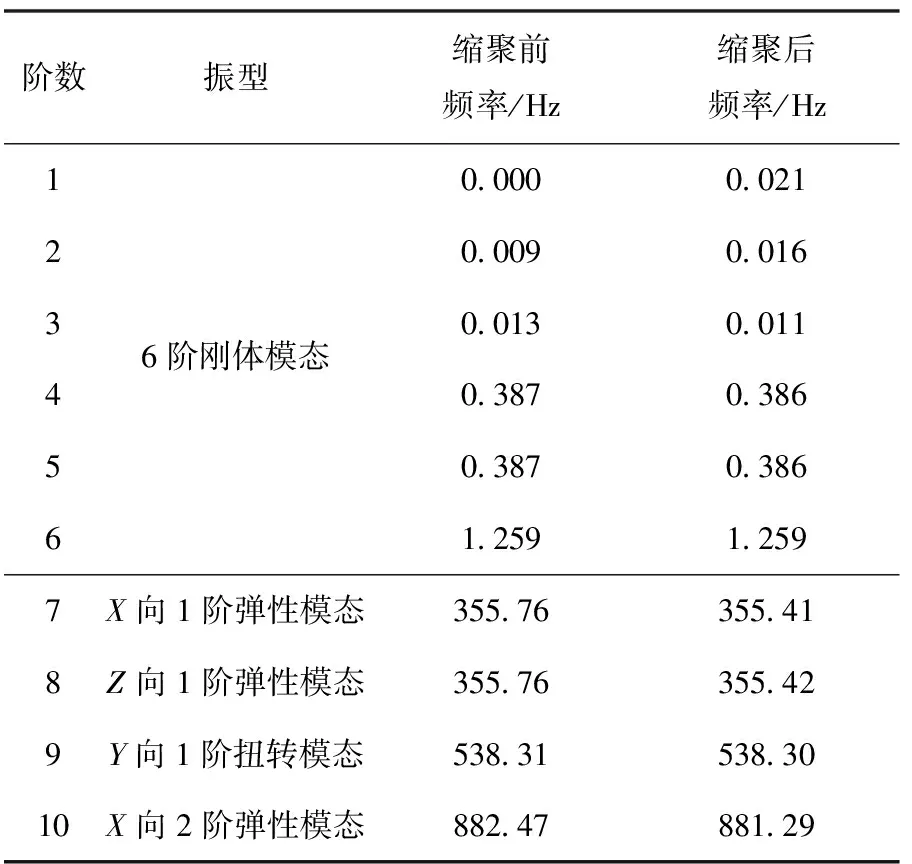
表1 某氣瓶縮聚前后自由邊界條件下的固有頻率對比Tab. 1 Comparison of natural frequencies forthe original and reduced models of a gas tank in free-free boundary condition

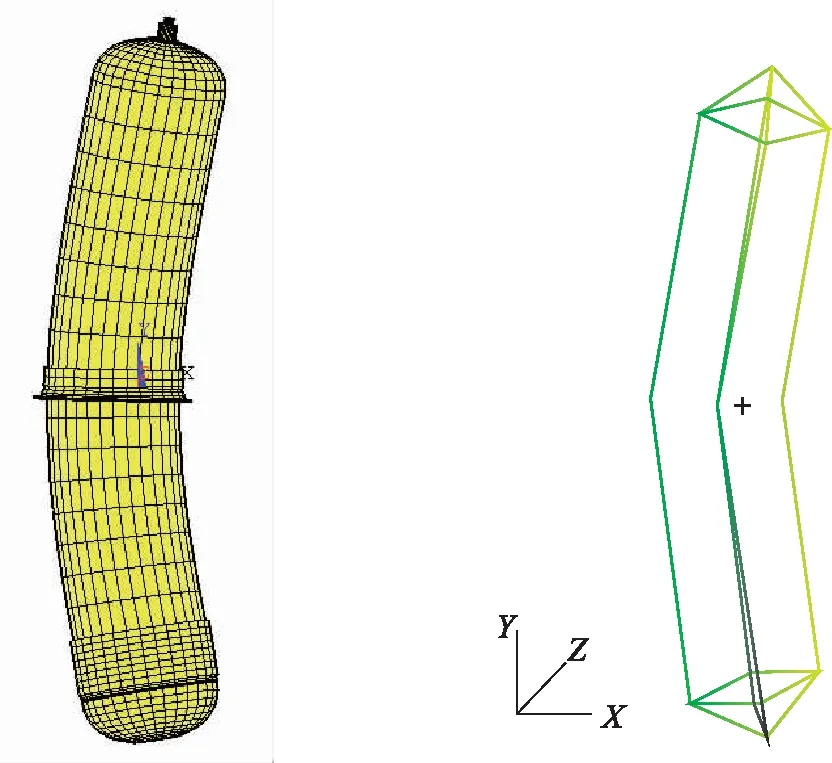
圖5 某氣瓶縮聚前后自由邊界下第7階模態振型對比圖Fig.5 Comparison of the 7th modal shapes for the original and reduced models of a gas tank

4 縮聚/物理混合模型的二級縮聚問題

耦合載荷分析(Coupled Load Analysis，CLA)是航天器研制過程中與運載火箭協同開展的一項極為重要的分析工作。流程是：先將航天器的有限元物理模型利用模態綜合法縮聚到航天器與火箭的連接界面上；然后將航天器的縮聚模型提供給運載方，由運載方完成航天器模型和火箭模型的裝配，并仿真分析出火箭飛行過程中器箭界面處和航天器內部典型位置的動力響應。

本文采用Matlab和Nastran DMAP二次開發語言實現了航天器縮聚/物理有限元混合模型的二級縮聚，并開展了虛擬耦合載荷分析驗證。作為示例，圖6給出了某衛星縮聚/物理有限元模型，該模型包含1個一級縮聚天線，安裝在衛星+Z側艙板上；其余部組件和星本體結構均為有限元物理模型。使用二級縮聚方案對該模型進行二級縮聚前后的固有頻率對比如表2所示；其中縮聚前后，前6階剛體模態在各個自由度方向的模態有效質量百分比之和均為100%。對比結果顯示了二級縮聚方案的正確性。

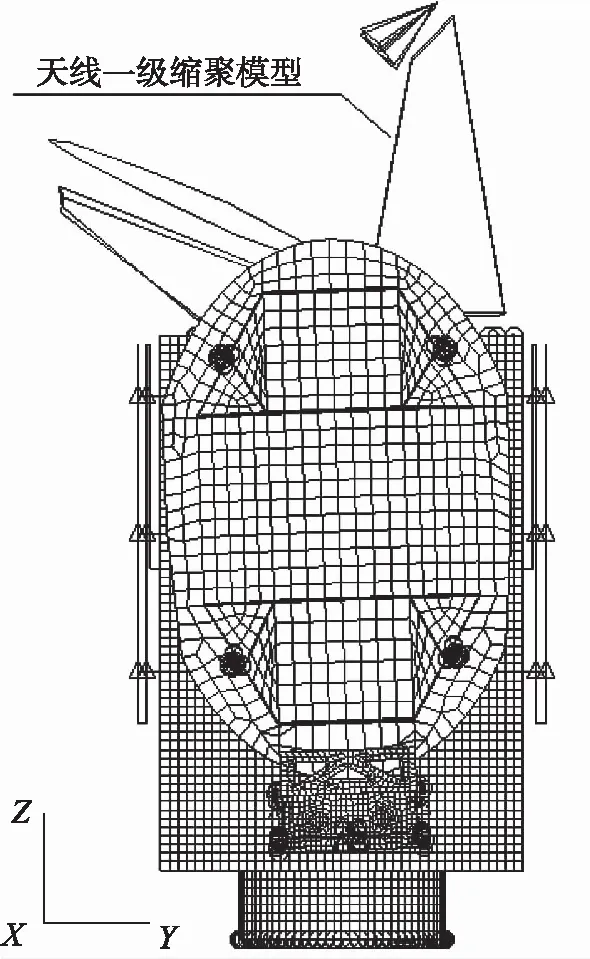
圖6 某衛星縮聚/物理混合模型Fig.6 Another hybrid finite element model of a satellite contained both unreduced and reduced sub-structures

為了進一步驗證二級縮聚解決方案在CLA中的正確性，把衛星的有限元縮聚/物理混合模型和二級縮聚模型分別裝配到一個相同的虛擬火箭模型上，再分別施加相同的虛擬氣動力進行虛擬CLA(見圖7)以對比分析結果。圖8給出了虛擬CLA在星箭界面點X向自由度的典型響應曲線，高度一致的對比結果證明了本文二級縮聚方案的正確性。

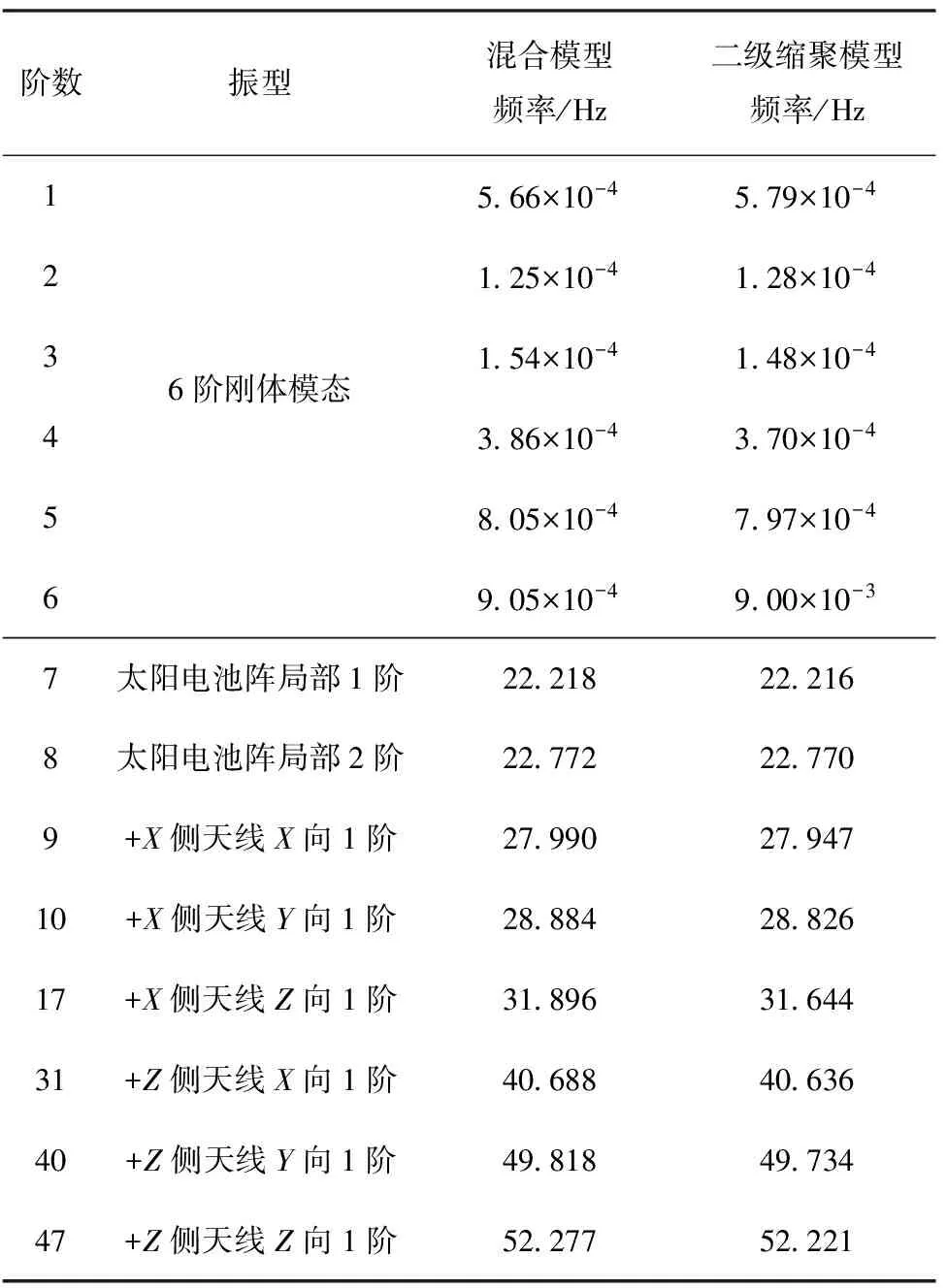
表2 某衛星有限元縮聚/物理混合模型和二級縮聚模型在自由邊界條件下的固有頻率對比Tab.2 Comparison of natural frequencies for the hybrid satellite model and its second-time reduced model in free-free boundary condition

圖7 器箭耦合載荷分析二級縮聚模型的驗證示意圖Fig.7 A pseudo coupled load analysis for the verification of an obtained second-time reduced model

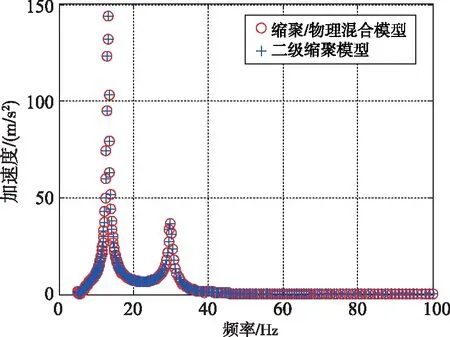
圖8 衛星混合模型和二級縮聚模型的虛擬CLA結果對比Fig.8 Comparison of a pseudo coupled load analysis results for the hybrid satellite model and its second-time reduced model

5 結論

本文簡要介紹了模態綜合法的基本原理和在國內外航天領域的應用發展，重點研究了模態綜合法在航天領域結構動力學分析應用中受限的兩個問題：1) 通過采用Fortran/Matlab混合編程實現Nastran的混合界面模態綜合法，將ANSYS版本的有限元物理模型直接縮聚為Nastran可識別的一級縮聚模型，從而初步解決了航天器部組件有限元模型的一級縮聚接口匹配問題；2) 通過Matlab和Nastran DMAP二次開發語言，初步解決了包含一級縮聚部組件模型的航天器縮聚/物理混合模型的二級縮聚問題，并通過虛擬耦合載荷分析證明了二級縮聚方案的正確性。相關技術成果可拓寬模態綜合法在我國航天器結構動力學分析中的應用范圍，并進一步促進我國航天器總體技術設計能力的提高。

[1] Hurty W C. Vibrations of structural systems by component-mode synthesis[J]. Journal of the Engineering Mechanics Division, ASCE, 1960, 86(4)：51-69.

[2] Bampton M C C, Craig R R. Coupling of substructures for dynamic analysis[J]. AIAA Journal, 1968, 6(7)：1313-1319.

[3] Hou S N. Review of model synthesis techniques and a new approach[J]. Shock and Vibration Bulletin, 1969, 40(4)：25-39.

[4] MacNeal R H. A hybrid method of component mode synthesis[J]. Computers & Structures, 1971, 1(4): 581-601.

[5] Rubin S. An improved component-mode representation[J]. AIAA Journal, 1975, 13(8)： 995-1006.

[6] Hintz R M. Analytical methods in component modal synthesis[J]. AIAA Journal, 1975, 13(8)：1007-1016.

[7] Majed A, Henkel E E, Wilson C. Improved method of mixed-boundary component-mode representation for structural dynamic analysis[J]. Journal of Spacecraft and Rockets, 2005, 42(5)：825-831.

[8] CraigJr R R. Coupling of substructures for dynamic analyses: an overview[R]. AIAA 2000-1573, 2000.

[9] Del Basso S, Singh S K, Lindenmoyer A J. A superelement methodology for coupled loads analysis of Space Station Freedom[C]. 31stStructures, Structural Dynamics and Materials Conference, 1990.

[10] DeWeck O L. Integrated modeling and dynamics simulation for the next generation space telescope[D]. Boston：Massachusetts Institute of Technology, 1999.

[11] 馮振興. 模態綜合法在大型、復雜宇航結構振動特性分析中的應用[C]. 第三屆全國振動理論及應用學術會議, 1987.

[12] 杜飛平, 譚永華, 陳建華, 等. 航天器子結構模態綜合法研究現狀及進展[J]. 火箭推進, 2010, 36(3)：39-44.

[13] 邱吉寶, 張正平, 李海波, 等. 動態子結構法在航天工程中的應用研究[J]. 振動工程學報, 2015, 28(4)：510-517.

[14] 史紀鑫, 曲廣吉. 可變構型復合柔性結構航天器動力學建模研究[J]. 宇航學報, 2007, 28(1)：130-135.

[15] 賈海濤, 馬洪亮, 吳清文, 等. 超單元在大型復雜航天相機結構中的應用[J]. 微計算機信息, 2009, 25(24)：161-163.

[16] 錢志英, 羅文波, 阮劍華. MSC.Nastran子結構法在航天器結構動力學分析中的應用[J]. 航天器工程, 2011, 20(5)：55-60.

[17] 葛東明, 鄒元杰, 史紀鑫. 固定界面模態綜合法在空間復雜結構系統中的應用研究[C]. 五院航天動力學論壇第二屆學術研討會, 2016.

[18] 馬興瑞, 韓增堯, 等. 衛星與運載火箭力學環境分析方法及試驗技術[M]. 北京：科學出版社，2014.

[19] Nastran M S C. Superelement user’s guide[R]. Moscow, MSC Public, 2013.