借教材練習掃盲點，實現計算“小目標”

吳靜媛

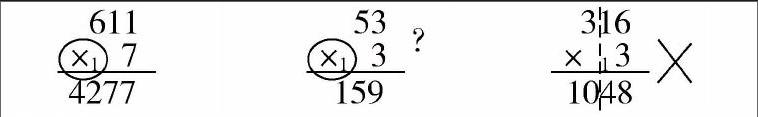
【摘要】通過使用人教實驗版和人教課標版（2011年版）的教學實踐，本人發現：在運用人教版數學教材時，需要教師能夠靈活選擇、變通、創造性地使用教材.本文結合“多位數乘一位數”的教學案例，先分析教材和學情，然后結合案例闡述在教學設計和教學過程中怎樣創造性地使用教材及使用效果.

【關鍵詞】借；變；計算；盲點

本人在近幾年的教學過程中，陸續使用了兩個版本教材，發現無論是人教實驗版和人教課標版（2011年版）教材，都更新穎、更具靈活性，在知識結構、呈現方式、教學方式和評價體系上都有較大突破和創新.這也給教師提出了更大的挑戰性，有很多地方需要教師延伸、拓展、創造性地使用教材.創造性地使用教材要求教師在充分了解和把握課程標準、學科特點、學生情況、教學目標的基礎上，以教材為載體，靈活有效地組織教學.

【問題呈現】

運算能力在《數學課程標準（2011年版）》中被作為核心概念重提，會算法、懂算理，這兩個運算能力的重要組成部分也再次受到大家的廣泛關注.但是，從教學中我們經常會碰到如此情況，教師重視了算理的教學，學生也能說出基本的算理、能模仿例題進行類似的計算，可是遇到含有“進位”“退位”等較復雜的計算時，學生錯誤率就會大幅提高，錯誤種類增多，在計算錯例中仍能發現一些頻次比較高的類型.由此，我們發現在學生對算理“聽得懂”“講得出”“想得到”之間還有一些距離.我一直在思考和尋找，期許能有所收獲.

【教材分析】

人教課標版義務教育教科書關于多位數乘一位數筆算部分安排在三年級上冊第六單元.這部分內容是本單元教學的重點，它是多位數乘法的基礎，同時在日常生活中有廣泛應用.教材在幫助學生借助操作活動理解筆算算理的基礎上，采取各個突破的辦法來克服筆算乘法的難點.例題分兩個層次編排：（1）通過“兩位數乘一位數（不進位）”——例1，引出筆算豎式，幫助學生理解筆算的算理；（2）通過“兩位數乘一位數（進位）”——例2、例3，“三位數中間（末尾）有0的乘法”——例5、例6.突破筆算乘法的難點.主要解決兩個問題：一是進位問題，二是因數的中間和末尾有0的問題.在進位中，先出不連續進位的，再出連續進位的，兩種情況都以兩位數乘一位數為主.這樣編排重點突出，分散了難點，便于學生在已學知識的基礎上，用類推的方法掌握知識.

【學情分析】

學生在一年級已學習了20以內加、減法.另外，學生在二年級學習了乘法的意義，并能運用口訣口算一位數乘一位數.但對學生而言，筆算乘法與筆算加、減法有很大差異，在計算過程中，多位數乘一位數不只是相同數位上的數相乘，而是要用一位數分別去乘另一個乘數的每一位，再把所得的積相加.計算步驟較多，需要注意的問題也很多，學生在計算過程中往往能說出“相同數位對齊”“從個位乘起”“注意進位”等事項，但在具體計算中“如何理解豎式中每一步計算的含義”“如何注意”，卻是個難點.特別是部分學生提前學習了筆算方法，會出現教師講，學生就響應，但讓學生自己講算理卻說不清、算不明的情況.兒童心理發展的規律表明，小學生的知覺常常出現籠統、局部、不精準的特點，特別是計算過程中缺乏耐心或急于求成，很難在具體問題中充分調用對算理的具體理解，更易受到題目中某些數據特點的影響.

如，三年級上冊“多位數乘一位數”中進位數寫錯錯例.

錯例中不難發現，學生對“要不要進？”“向哪一位進？”“進幾？”這樣的問題缺乏足夠的思考.

【教材使用案例及效果】

借練習變數學課堂“問題引領”，使學生看到自己的思考.

新課標要求：“不同的人在數學上得到不同的發展.”因此，教師應有意識地將學生的認知發展水平及已有經驗與新知識進行對比，將問題分層次在全體學生中平穩分布.

一、設計有效復習問題，加速從舊到新

通過與新知有聯系的舊知復習，喚起學生回憶，有效搭建通往新知的橋梁，才能使學生的思維由“未知區”向自己的“最近發展區”，最后向“已知區”轉化.

如，，也就是（ ）.

避免學生只看數位上的數字不想數值，同時促進學生自己理解為什么十位上滿十向百位進位.學生在計算多位數的每一位與一位數相乘時，直接用口訣，而不會去算幾十或幾百乘一位數，計算的結果需要進位時部分學生就將口算結果直接寫在相應的位置.

二、鋪設小目標問題，使學生能拾級而上

學生已有的知識水平和思維特點不同，問題由易到難，由淺入深，由形象到抽象，層層遞進，這樣才能使不同層次的學生思維充分暴露，設置有針對性、有層次性的問題，將目標細化.

1.算理過程填空練習，暴露學生對算理的提取過程，縮小自覺化的快慢差距.

教室內不應該出現“被遺忘的角落”，要“設臺階、展過程、示學法、預生成”，要鼓勵所有的學生認真思考，使不同層次的學生都有回答問題的愿望.邏輯思維強、綜合思維強的學生能較快地理解算理，并能連貫地表達算法的每個步驟.但對于綜合思維不那么強的學生，需要有提示作為抓手幫助他們提取算理流程，并借助下面這樣的直觀形成具體表征.

想一想，填一填.

2.題組對比練習，暴露學生計算的每一步以及步與步之間的銜接的原生態思考，幫助學生更了解自己的解析過程和解析特點.

教材61頁例2中出現 ，在隨后的“做一做”中出現了 ，這幾題看似都圍繞著多位數乘一位數（進位）這一課時目標，實則有多位數數位不同，進而進位位置不同，以及多位數位數不同積的位數也不同這樣的小目標.因此，在教學時，我有意將這些意圖呈現在變式練習中（見下圖），通過對比理解算理相同，但在具體計算時遇到不同的情境要做相應的變化，從而使學生盡早發現小目標與大目標之間的聯系和區別.

從個位滿一十向十位進一到十位滿一十向百位進一，再到十位滿二十向百位進二，學生能直觀地看到進位位置和數值的變化，也能較快地梳理出“哪一位滿幾十就向前一位進幾”這樣的規律.

綜上所述，在教學中想要重視算理算法，進行合理調整和補充，就要真正做到基于教材又不拘泥于教材，既要深入分析教材，又要“跳出”教材，以更寬闊的視野“重塑”教材.只有清掃學生思維盲點，通過一個個課時學習學生在一些小點上算理更清，計算時朝著更準、更快的方向提高學習能力和學習效率，才能進而積累達到培養運算能力、提高核心素養的大目標.

【參考文獻】

[1]溫寒江，陳立華，魏淑娟.小學數學兩種思維結合學習論：馬芯蘭教學法的研究與實踐[M].北京：教育科學出版社，2016.

[2]人民教育出版社，課程教材研究所小學數學課程教材研究開發中心.義務教育教科書·數學·三年級（上冊）[M].北京：人民教育出版社，2014.

[3]人民教育出版社，課程教材研究所小學數學課程教材研究開發中心.義務教育教科書·教師教學用書·數學·三年級（上冊）[M].北京：人民教育出版社，2014.

[4]教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[5]潘可可，唐彩斌.發展學生運算能力應當“法理并重”[J].小學數學：教學版，2016（5）：13-15.

[6]鄢曉欽，劉自強.悟教材之本，成教學之實——以新理念指導教材分析[J].小學教學研究，2016（10）：10-13.