一種耦合外部電路的脈沖感應推力器磁流體力學數值仿真模型?

車碧軒 李小康 程謀森 郭大偉 楊雄

(國防科技大學航天科學與工程學院,長沙 410073)

1 引 言

脈沖感應推力器(pulsed inductive thruster,PIT)是一種通過脈沖感應電磁場電離和加速等離子體從而產生沖量的空間電推進裝置,具有工質適用范圍廣、比沖效率較高、負荷大功率、推力變比高等諸多優點,是未來行星際空間貨物運輸或載人深空探測任務的優選推力器之一,近年來引起了廣泛關注[1?4].PIT尺寸較大,工作電壓達數十千伏,需要在高真空環境下開展實驗,實驗系統十分復雜;其所涉及的等離子體過程具有微秒尺度的強瞬態特性,諸多等離子體診斷手段并不適用.因此,數值仿真成為研究PIT中等離子體瞬態參數特性、預測其推進性能的重要手段.

PIT的單個脈沖工作過程中存在驅動電路放電和等離子體感應加速兩類基本物理過程,二者通過激勵線圈產生強烈的感應耦合作用.Lovberg和Dailey[4?6]最早提出機電模型,將電路和等離子體依次等效為變壓器的主次級,并將等離子體視作質量不斷增長的“雪耙”電流片,建立集總參數的電流片運動及電路方程組求解;Polzin等利用機電模型研究了推力器性能優化的動態參數匹配問題[7,8],并引入對Ar等離子體物性參數的計算[9];Martin等[10]將其適用范圍由平板型線圈拓展至錐形.機電模型能較好地反映電路與等離子體之間的耦合關系,但忽略了復雜的等離子體參數分布,計算結果不夠準確;還存在初始電流片厚度、電流片-激勵線圈互感等諸多關鍵參數需要根據實驗甚至經驗給出,其計算結果的正確性難以判斷[11].針對這一缺陷,近年來開始采用二維軸對稱的磁流體力學(magnetohydrodynamic,MHD)模型計算等離子體感應加速過程:Mikellide等[12?14]利用MACH2代碼對NH3工質的推力器MK-Va進行了數值仿真,其依據實驗所得電路電流曲線給出MHD中的時變磁場邊界條件,計算所得推力器單脈沖沖量及放電前1/4個周期內的等離子體瞬態磁場分布與實驗數據均能較好地匹配;成玉國等[15,16]采用M-AUSMPW格式計算了正弦時變磁場激勵下Ar等離子體的瞬態參數分布,證實在感應加速過程中等離子體形成了“雪耙”型的電流片結構.相較于集總參數的機電模型,MHD模型側重于對等離子體流場形態進行計算,考慮了復雜的各類等離子體物理過程,計算結果更加可靠.然而,已有各類MHD模型均采用外部給定的瞬時磁場邊界條件驅動等離子體,沒有考慮等離子體對電路的反向耦合作用,隨著計算時間的推進,計算結果會逐漸偏離實際[14],因此計算結果的準確性有待提升.綜上,對于PIT這樣一個涉及強瞬態等離子體流動過程且電路-等離子體高度耦合的復雜系統,數值仿真研究還有待進一步拓展.

本文結合兩類數值仿真模型的優缺點,在COMSOL平臺中建立了一種耦合外部電路的二維瞬態軸對稱MHD模型并開展數值仿真研究.本文第二部分系統介紹了PIT的工作原理以及數值模擬所采用的物理模型;第三部分對比了模型計算結果與文獻實驗數據,驗證了計算結果的有效性;第四部分對計算結果進行了分析與討論,合理解釋了PIT的工作物理圖景,并對電路與等離子體之間的雙向耦合作用進行了分析;第五部分為總結.本文建立的數值仿真模型實現了對驅動電路放電過程和等離子體二維流場形態演化過程的同步耦合求解,計算結果更加可靠、準確.模型可用于研究PIT的工作原理,預測其推進性能,為推力器結構設計、參數優化提供了技術支持和可行的計算方法.

2 模型簡介

2.1 工作原理

圖1 美國TRW公司MK-1推力器 (a)推力器實物照片[26];(b)激勵線圈構型及線圈面板Fig.1.American TRW Company’s MK-1 thruster:(a)Photograph of the thruster assembly;(b)drive-coil con fi guration and coil-faceplate.

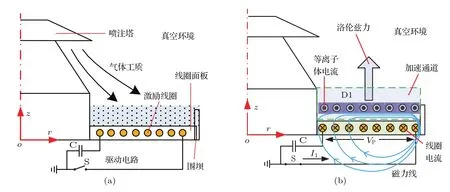
圖2 PIT工作原理示意圖 (a)氣體噴注;(b)感應加速Fig.2.Schematic plot of PIT’s working principle:(a)Gas injection;(b)inductive acceleration.

以美國TRW公司1 m直徑的推力器MK-1作為數值模擬對象,其基本結構如圖1(a)所示,由噴注塔、激勵線圈、電容組C、開關S等組成.其中,激勵線圈如圖1(b)所示,一般由多組螺旋線形導線按軸對稱方式并聯排布而成,再封裝于絕緣材料制成的平板型線圈面板中以避免和等離子體直接接觸.推力器的工作原理如下:如圖2(a),首先噴注塔以脈沖方式將數毫克氣體噴注至線圈面板表面使其達到較為均勻的徑向分布;緊接著如圖2(b),在氣體噴注完成瞬間,S接通C放電形成迅速上升的脈沖強電流I1,電流通過激勵線圈在空間中激發徑向發散型的時變磁場;根據“法拉第”電磁感應定律,這一時變磁場將感生出周向閉合的渦旋電場;渦旋電場擊穿氣體并建立起周向閉合的等離子體電流;等離子體電流(垂直紙面向外)與線圈電流(垂直紙面向內)相當于兩個異號的電流片,其洛倫茲力相互排斥,從而對等離子體實現軸向加速;等離子體電流片在向前運動的過程中不斷電離和帶走下游氣體,最終噴射進入真空環境,完成一個工作脈沖.線圈對等離子體的有效耦合距離約數厘米,為了約束氣體在面板外徑處設置一圈與耦合距離等高的圍壩,圍壩所圍成的中空柱形區域即是等離子體的加速通道[12].

2.2 物理模型

2.2.1 模型總體方案

根據PIT工作原理及國內外已有研究成果,本文建立模型時所考慮的各類物理過程所具備的主要特征以及相應的假設和近似處理總結如下:1)假設等離子體電流只存在周向分量,且主要為電子電流,忽略離子電流;2)載流的電子受洛倫茲力作用與離子產生軸向空間電荷分離,離子的加速本質上由分離電場實現,但由于電子數密度較高,其分離尺度相較于電流片尺度可以忽略,電子和離子視作單一流體被加速,滿足等離子體的宏觀電中性條件[5];3)圍壩、線圈面板、噴注塔等表面不存在明顯燒蝕,鞘層現象被證明可以忽略;4)電子和離子幾乎處于熱力學平衡狀態,等離子體溫度可達2 eV以上,存在顯著的多級電離和等離子體輻射[12].

本文借助多物理場仿真平臺COMSOL MultiphysicsTM建立和求解計算模型,采用如圖3所示的二維軸對稱計算區域,假設等離子體只存在于激勵線圈前側的矩形加速通道域D1內(對應圖2(b)虛線內);激勵線圈則等效為長條形區域D2,具有垂直于紙面方向的周向電流密度分布jC,θ;噴注塔、圍壩、線圈面板及推力器工作時所處的真空環境等因其電導率均為0而統一作為真空域D3;為了準確計算推力器磁場在空間中的分布,D3尺寸遠大于D1,D2.

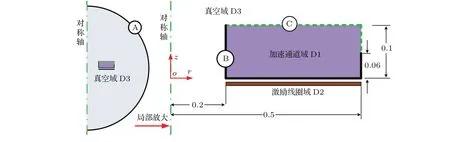
圖3 計算模型區域劃分與邊界Fig.3.Computational domains and boundaries.

圖4 計算模型中所采用的各物理場耦合關系及模型求解流程Fig.4.Coupling relationship between physical fi elds in the computational model and its solving fl ow chart.

對應的模型多物理場耦合關系及求解流程如圖4:第一步,考慮如圖2所示的驅動電路,設激勵線圈端口間的電勢降為VP,建立集總參數的電路方程組計算線圈總電流I1,其中,VP根據D2的周向感應電場強度Eθ分布及激勵線圈幾何構型計算;第二步,根據激勵線圈幾何構型及I1,計算D2中的等效線圈電流密度分布jC,θ,將jC,θ作為外部電流密度施加至D2,采用磁場模塊同時計算D1,D2,D3組成的半圓形區域磁場分布,再單獨計算D1的歐姆熱功率密度j2/σ和洛倫茲力密度j×B,以及D2中的周向感應電場強度Eθ;第三步,將j2/σ和j×B分別作為體積熱源項和體積力項引入Navier-Stokes(N-S)方程組中的能量方程和動量方程,采用高馬赫數流動模塊計算D1的溫度T、壓力p等狀態參數分布及速度分布u,從而實現對MHD過程的求解.其中,A○為磁場邊界,B○,C○依次為流場的壁面和出口邊界.

特別地,D1區域所涉及的等離子體其電離組分不斷變化,等離子體的熱力學性質、輸運性質等隨等離子體狀態不同而有很大差異.假設其處于局部熱力學平衡狀態(local thermal equilibrium,LTE),電子和重粒子組分具有相同的溫度T,給定狀態參數(p,T)即可惟一確定等離子體的組分及各項物性參數.本文基于LTE模型預先計算出Ar等離子體在p=1—106Pa,T=298—105K參數范圍內的電離組分及物性參數,將其制作為按(p,T)索引的二維插值數表,在每一時間步更新.

2.2.2 控制方程組

1)磁場控制方程

磁場控制方程應用于圖3所示的所有計算域,其基本形式如下:

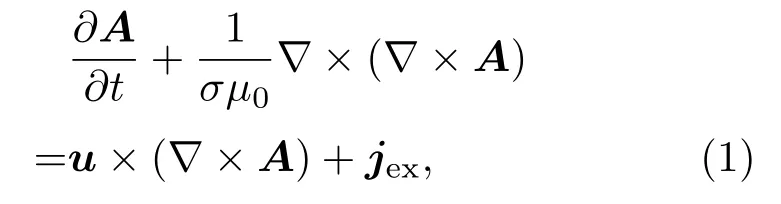
式中,磁場通量密度B采用矢量磁勢A(B=?×A)形式求解,從而避免了在MHD數值計算中因磁場散度清除條件?·B=0限制帶來的數值誤差[17];σ,μ0表示電導率、真空磁導率;u為速度矢量;u×(?×A)表示由導體宏觀定向運動引起的感生電場,該項只在D1中存在;jex表示外部電流密度分布矢量,該項只在D2中存在且只含周向分量,等于線圈電流密度分布jC,θ.

2)流場控制方程組

采用可壓縮黏性流體控制方程組,只在D1域求解,具體形式如下:

連續方程

動量方程

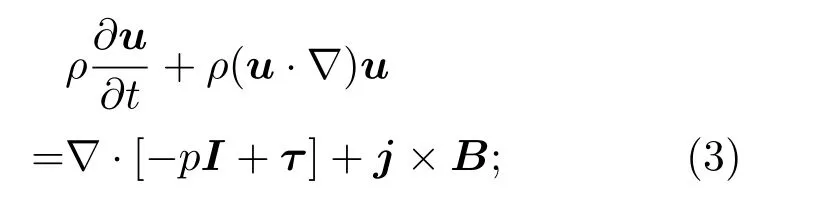
式中,ρ為密度,I為單位對角張量,τ為黏性應力張量,B為磁感應強度j×B為洛倫茲力體積力;能量方程[18]

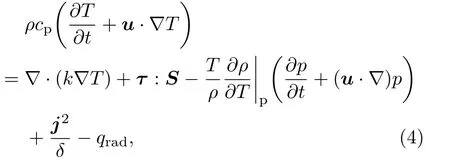
式中,cp表示等離子體定壓比熱,k為等離子體熱導率,S為流體微元應變張量;等號右邊五項依次為熱傳導項、黏性耗散項、壓力耗散項、等離子體歐姆熱源項、等離子體輻射損失項qrad.

3)狀態方程

在COMSOL中采用如下形式的氣體狀態方程:

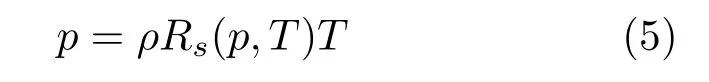
其中,在常溫下Rs一般表示理想氣體常數;對于本文涉及的高溫電離氣體,因其存在多級電離組分,Rs不再是常數,而是等離子體狀態參數(p,T)的函數[19],Rs計算方法將在后文闡述.

4)電路控制方程組

考慮圖2所示的驅動電路建立集總參數的電路方程組:

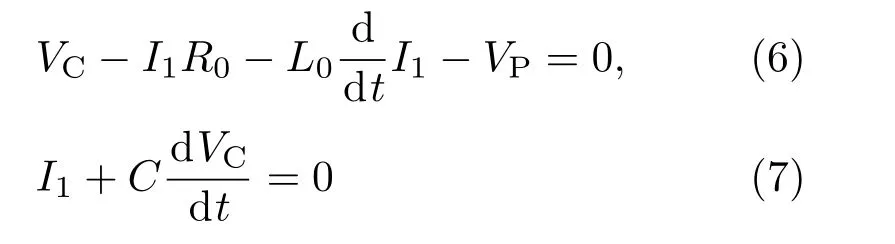
其中,I1為驅動電路總電流,IP為等離子體總電流,R0為電路寄生電阻,L0為電路寄生電感,C為電容組總容值,VC為電容電壓,VP為激勵線圈端口間的電勢降.

5)電路-等離子體雙向耦合參數計算方程

驅動電路與等離子體通過激勵線圈相互耦合,耦合參數jC,θ,VP分別表示電路對的等離子體的激勵與反饋作用,與激勵線圈的幾何構型緊密相關.對MK-1的激勵線圈,其單支螺旋線可表示為如圖5所示的等速螺旋線,導線由線圈外側r2處回繞至r1處,再由絕緣面板的背側連出.其兩端IO通過同軸電纜與電容及開關相連,螺旋線線形可表示為

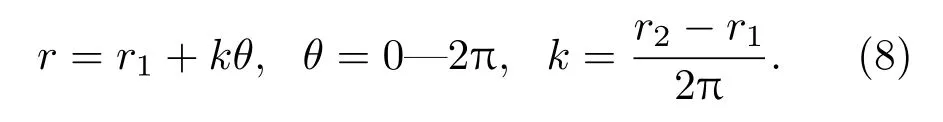
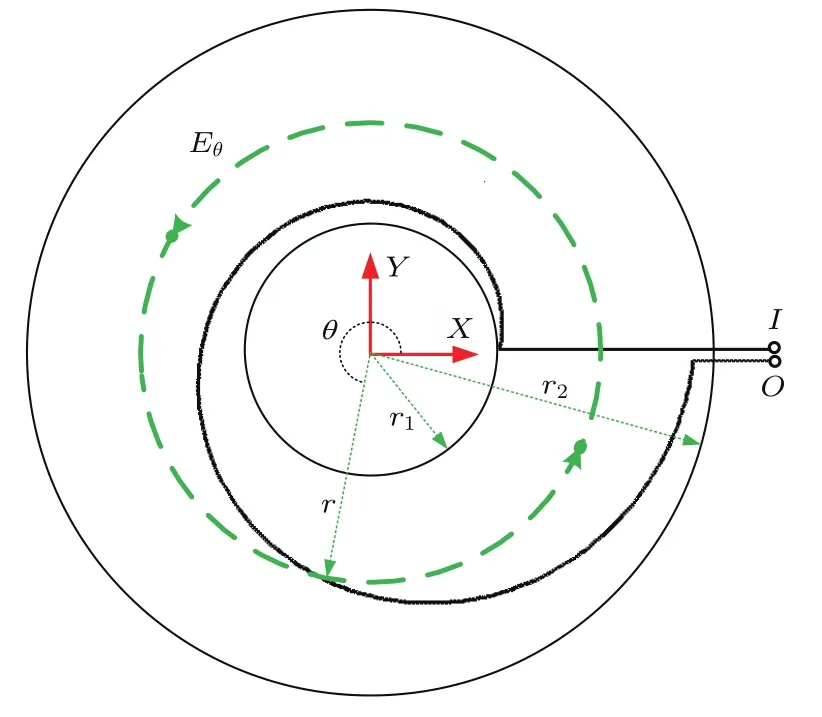
圖5 激勵線圈中的單支螺旋線導線幾何形狀Fig.5.The geometry of one individual spiral conductor in drive-coil.

激勵線圈域D2中任意位置處的等效周向電流密度jC,θ可表示為

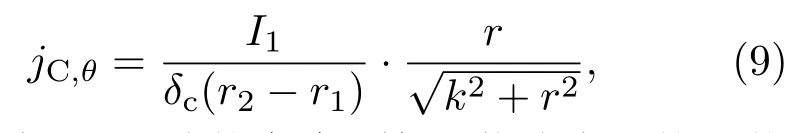
式中,δc為D2區域的高度,等于激勵線圈的導體直徑.

激勵線圈端口電勢降VP則等于周向電場強度Eθ沿螺旋線導線的積分,

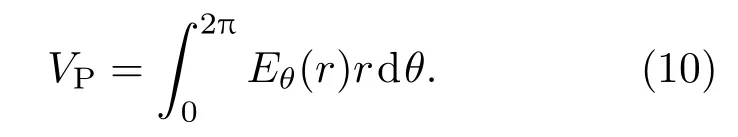
對上式做積分變換可得適用于二維軸對稱的表達式:

其中,Eθ可根據磁場分布情況由式Eθ=(??A/?t)θ計算.

2.2.3 初邊值條件

1)初值條件

電路控制方程組初值條件:初始電路電流I1=0,初始電容電壓V=V0.

D1,D2,D3域磁場初值條件:A=0.

D1域流場初值條件:本文不考慮中性氣體的擊穿過程,假設在初始時刻加速通道內的工質已被輕度電離,其等離子體溫度T=0.5 eV;根據室溫下給定的中性氣體密度分布,計算其T升高至0.5 eV時的p分布,以之作為p分布的初值條件.

2)邊值條件

對于磁場邊界條件,由于三部分計算子域磁場是連續的,故只需給出圖示邊界A○的磁場邊界條件,這里采用磁絕緣邊界條件;對于流場邊界條件,線圈面板、噴注塔及圍壩組成的壁面B○采用速度無滑移、絕熱壁面邊界條件;開口邊界C○采用遠場邊界條件.

2.2.4 等離子體物性參數

1)電離組分

計算等離子物性參數,首先需要獲得其電離組分,針對Ar工質在LTE假設下考慮6級平衡電離復合反應,聯立沙哈平衡方程組(12)、電荷守恒方程(13)及混合組分氣體狀態方程(14)求解[9]:

式中,ne表示電子數密度;ns表示s級(s=0—6)電離離子數密度,特別地,當s=0時n0表示中性原子數密度;me為電子質量;κB為玻爾茲曼常數;h為普朗克常數;εsl為s級電離離子的第l能級,gsl為相應的統計權重.

2)熱力學參數

根據電離組分的數密度計算等離子體總ρ,得到其Rs(p,T):

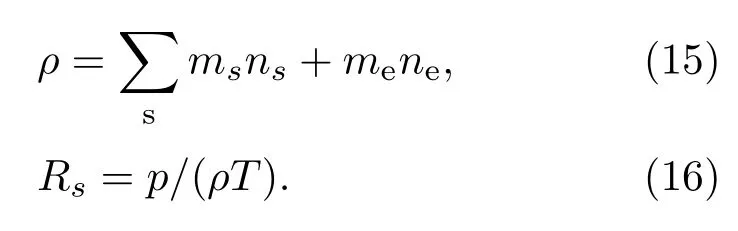
cp通過比焓ht計算[20]:

對于單原子分子等離子體,ht由平動能貢獻htran,重粒子內部電子的激發能貢獻hex及電離離子的電離能貢獻hi組成:

各部分貢獻的計算式依次為:

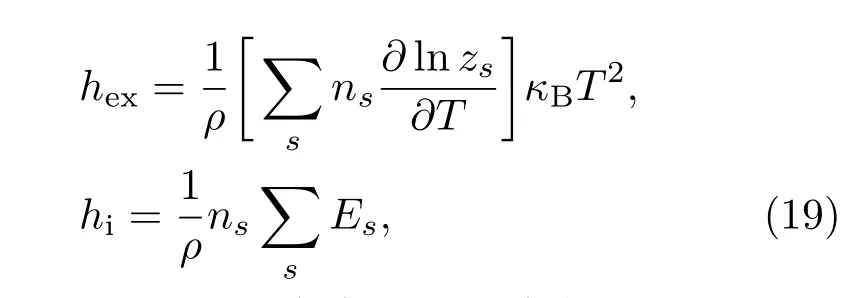
式中,Es表示s級電離離子的電離能,zs表示s級電離離子的內部配分函數.

3)輸運系數

在等離子體的輸運性質中,電導率是極其重要的一種,本文所涉及的等離子體可能處于完全電離或弱電離之間的任意電離狀態,需要同時考慮長程碰撞和短程碰撞的作用.忽略磁場對電導率的影響,假設電導率為各向同性的標量σ,采用Kantrowitz[21]提出的電導率并聯模型計算復合電導率:

其中,Spitzer[22]給出了完全電離等離子體的電導率σc計算公式:

對于弱電離等離子體電導率σw,采用經典碰撞理論計算:

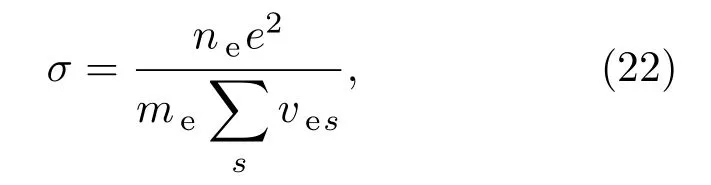
式中e為電子電荷量,ves為能量加權平均的電子和s級電離離子之間進行動量交換的碰撞頻率[23,24].

對于等離子體輻射,其光學厚部分作為等離子體熱傳導的一種增強機制,依據文獻[25—27]計算了等離子體復合熱導率;其光學薄部分作為體積熱源項qrad引入能量方程.qrad及黏性系數μ依據文獻[25]計算.

3 數值模擬與實驗數據對比

數值仿真所采用的初始ρ分布如圖6,取自文獻[26]給出的MK-1推力器實測值,對應的脈沖氣體質量mbit=15 mg,電容初始電壓V0=20 kV.為驗證計算結果的有效性,本文對比了不同時刻下徑向磁場強度Br沿內外徑中線處的軸向分布(圖7)、軸向洛倫茲力密度(j×B)z的二維分布(圖8)、推力器推力-時間曲線(圖9)以及V0=20—24 kV下的比沖Isp、效率η等性能參數(圖10)的數值仿真結果與實驗測量數據.

圖6 數值仿真所采用的加速通道初始氣體ρ/(kg/m3)分布,數據取自文獻[26]Fig.6.Initial ρ/(kg/m3)distribution in the acceleration channel used in simulation,data from reference[26].

3.1 徑向磁場強度Br

通常情況下,Br將隨軸向距離z的增大而按指數衰減,但在如圖7所示的2μs時刻z=0—0.02 m區間卻形成了磁場強度達0.35 T的均勻磁場區域.這是由于等離子體電流片的存在壓縮了其與激勵線圈之間的磁場.伴隨電流片逐漸遠離線圈,該均勻磁場區域的范圍逐漸擴大,磁場強度逐漸減小.數值仿真結果重現了這一磁場演化趨勢,同時在磁場強度的大小及軸向分布上也與實驗數據基本一致.

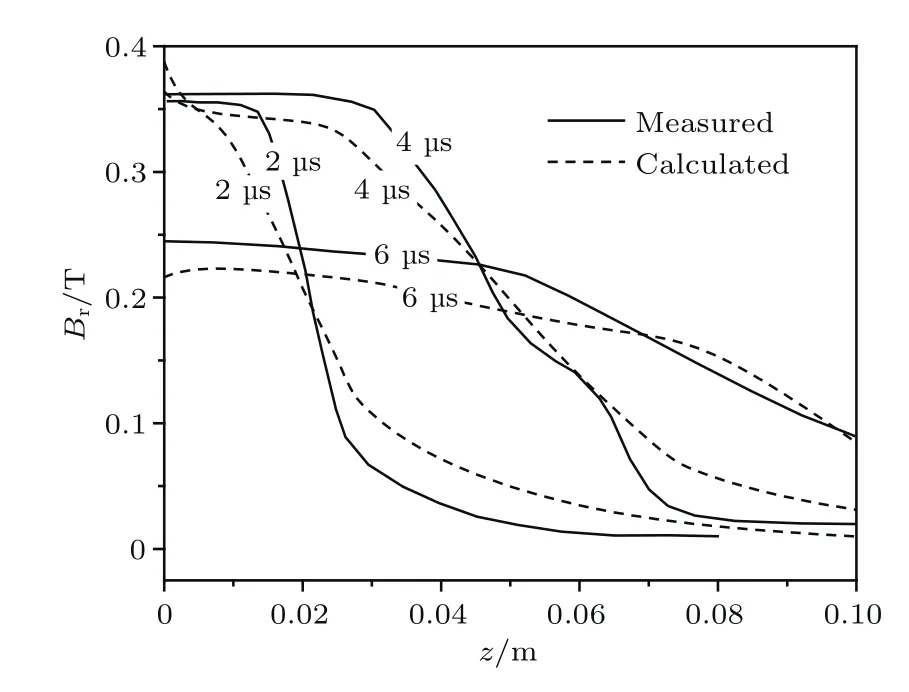
圖7 t=2,4,6μs時刻加速通道內外徑中線處Br計算結果與文獻[28]實驗數據Fig.7.Calculated and experiment measured[28]Bron the middle line of the acceleration channel at t=2,4,6μs.

3.2 軸向洛倫茲力密度(j×B)z

(j×B)z分布呈現出與Br不同的演化趨勢:其峰值區域在t=2μs首先出現在z=0附近;但在t=3μs,線圈附近的(j×B)z開始減小,其峰值區域向前推進,洛倫茲力的作用似乎穿透了均勻磁場區域而主要作用在電流片上;由于初始氣體ρ分布的不均勻,靠近內徑處的(j×B)z峰值區域運動得比靠近外徑處更快.圖8(b)所示的計算結果基本呈現出了與實驗數據一致的演化規律,其(j×B)z分布在t=2μs時刻與實驗數據符合較好,在t=3μs存在一定差異.

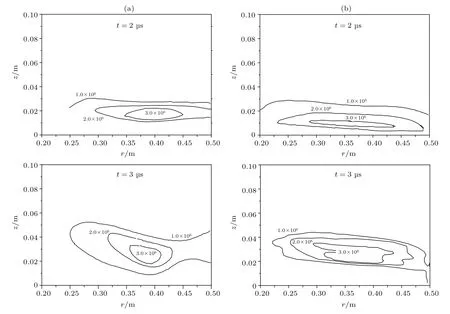
圖8 t=2,3μs時刻(j×B)z/(N/m3)分布文獻[26]實驗數據(a)與本文計算結果(b)Fig.8.Calculated(a)and experiment measured[26](b)data of(j×B)z/(N/m3)at t=2,3μs.

3.3 推力-時間曲線

將工質所受洛倫茲力在加速通道內做體積積分即可得到推力器的推力-時間曲線.由圖9可見,推力器的推力主要產生在0—9μs時刻,在9—10μs期間短暫為負,10μs之后再次為正并逐漸衰減.數值計算結果在趨勢及大小上均與實驗數據一致,表明數值仿真正確反映了推力器在不同時刻的整體工作狀態.

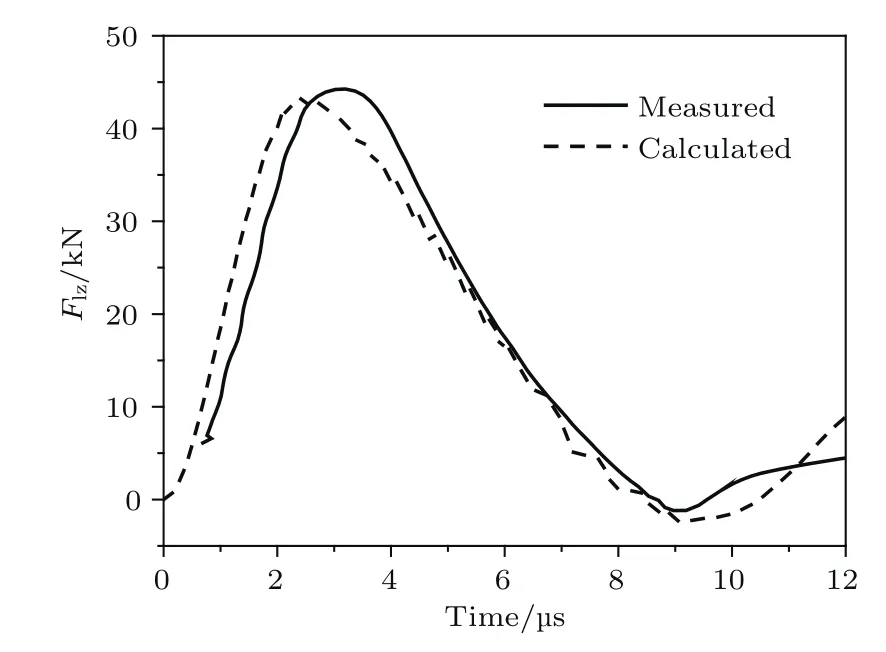
圖9 推力器-時間曲線計算結果與文獻[28]實驗數據對比Fig.9. Calculated and experiment measured[28]thrust vs.time.

3.4 不同放電電壓下的推力器性能

圖10給出了MK-1推力器在V0=18—24 kV下的推進性能實驗數據及計算結果對比,其中,單脈沖沖量I通過推力在0—20μs計算時間內的積分得到,比沖Isp=I/mbit,效率η為工質總動能與電容組儲能之比:

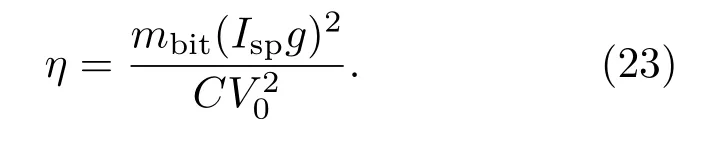
作為對比,圖中同時給出了Lovberg等[26]采用一維機電模型的計算結果.圖10表明,本文計算所得推力器性能略低于與實驗測量數據,但相較于“雪耙”模型的計算結果更加接近實驗結果,推力器性能隨V0的變化趨勢則與實驗數據基本一致.

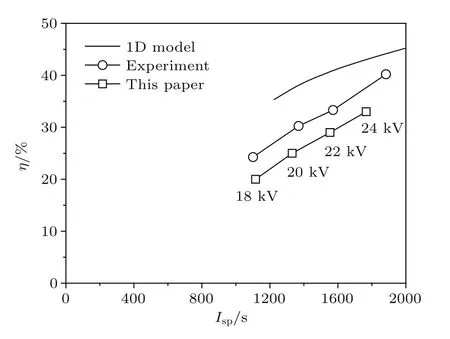
圖10 不同放電電壓下的推力器比沖Isp、效率η性能計算結果、實驗測試數據及一維“雪耙”機電模型計算結果對比Fig.10.Comparison of the thruster’s speci fi c impulse Isp and efficiency η:numerical results in this paper;experiment measured data in[26];numerical result from 1D circuit model in[8].

綜上,本文所采用的計算模型能較好地反映推力器工作過程中的各類物理過程,數值仿真成功復現了PIT的工作物理圖景,計算結果在等離子體瞬態參數分布、推力器工作狀態、推力器推進性能三個方面均與實驗取得了較好的一致.

4 計算結果分析與討論

4.1 推力器系統的工作物理圖景

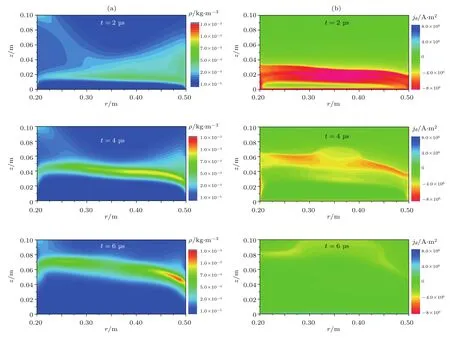
圖11 計算所得等離子體ρ分布(a)與jθ分布(b)Fig.11.Calculated plasma ρ (a)and jθ (b)distribution.

為了對推力器工作物理圖景建立更深刻的認識,圖11給出了不同時刻ρ和jθ的二維分布.如圖所示,t=2μs時激勵線圈附近產生了與線圈電流反向的(負號)等離子體電流jθ,jθ受洛倫茲力作用被軸向加速,帶動工質壓縮成片狀,同時在其后方留下了近乎真空的低ρ;由于這一區域ρ極低,載流電子較少,其σ也較低,因此電流片開始逐漸脫離線圈表面,線圈磁場也得以穿過這一區域,持續地對高ρ,高jθ的電流片區域進行加速;洛倫茲力在前期將等離子體壓縮成致密的片狀,伴隨電流片不斷遠離,激勵線圈磁場逐漸衰減,6μs時刻洛倫茲力不再足以維持其致密的片狀結構,電流片開始破裂,等離子體則向真空中自由膨脹.

4.2 電路-等離子體的雙向耦合作用

借助本文所建立的模型,可以實現對推力器工作過程中電路狀態與等離子體狀態的同步分析.圖12在同一坐標系內給出了驅動電路電流I1與等離子體總電流的相反數?IP隨時間變化的曲線,其中IP通過jθ在D1域的積分得到.由圖可見,在放電前期I1與?IP幾乎完全重合,隨后逐漸分離,但在變化趨勢上?IP始終跟隨I1.對應圖9所給出的推力-時間曲線可以得出,等離子體的感應加速主要集中在I1的前1/2個周期內I1與IP異號的階段;在9—10μs期間,I1與IP同號,推力為負;在10μs之后,I1與IP再次異號推力為正并逐漸衰減.這些現象表明,電路電流實際上決定了等離子體電流及等離子體的加速進程.另一方面,為了分析等離子體對電路電流的影響,本文通過在計算域中移除D1域計算了激勵線圈在真空下放電的空載電流曲線I?1.在圖12中對比I1與I?1可以見,耦合等離子體之后,I1相較于I?1振蕩周期明顯縮短,相當于其等效電感減小;圖13則給出了對應的空、負載放電狀態下的激勵線圈電勢降VP和V?P.由圖可見,耦合等離子體后VP顯著降低,且在t=0—2μs期間保持基本穩定,這一特殊現象說明VP受到了等離子體瞬時流場形態的影響.以上分析表明,在PIT工作過程中其驅動電路與等離子體相互影響,存在強烈的雙向耦合作用.

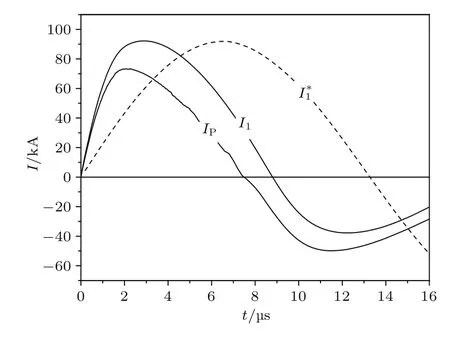
圖12 計算所得等離子體總電流IP與電路總電流I1隨時間的變化Fig.12.Calculated total plasma current IPand circuit current I1vs.time.

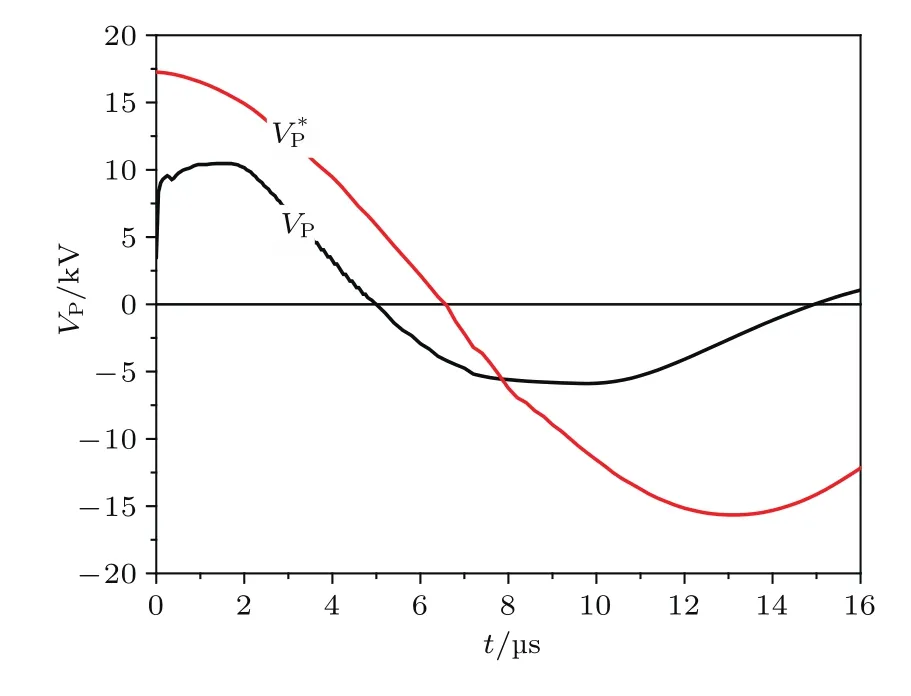
圖13 計算所得空、負載放電狀態下的VPFig.13. Calculated drive-coil VPwhen plasma is loaded or unloaded.

為了對這一雙向耦合作用進行定量化分析,首先將驅動電路和等離子體等效為如圖14的變壓器主次級.其中,LC為激勵線圈自感,LP為等離子體電流環自感,RP為等離子體等效總電阻;激勵線圈與等離子體之間的互感M體現了二者之間的感應耦合強度;顯然,LP,RP和M均將隨等離子體狀態參數及流場形態的演化而改變[6].

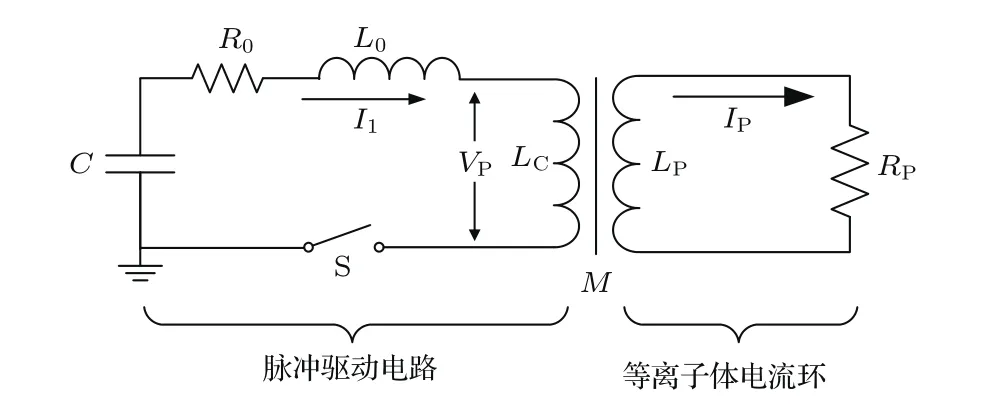
圖14 PIT電路等離子體系統的變壓器等效電路圖Fig.14. Transformer equivalent circuit scheme for PIT’s drive circuit and plasma load.

采用前期研究提出的方法[11]計算所得RP和M結果如圖15和圖16,下面對照已給出的等離子體jθ瞬態分布對電路-等離子體之間的雙向耦合作用進行定量分析:在放電初始時刻,激勵線圈表面附近建立起了環形的等離子體電流片,jθ因趨膚效應作用聚集在激勵線圈附近,與線圈電流幾乎重合,因而M≈LC=0.75μH;此后伴隨電流片被加速遠離線圈,M逐漸減小,其減小的速度也隨電流片運動速度的增大而增大;t=10μs時刻I1過零點附近,因jθ再次聚集于激勵線圈表面,M又開始迅速增大,隨后再次減小.Rp則體現了等離子體的總歐姆耗散,放電前;放電后0—6μs期間,Rp因氣體被持續電離而不斷減小;6—8μs伴隨感應耦合作用M的減弱,Rp開始增大;8—16μs再次下降.

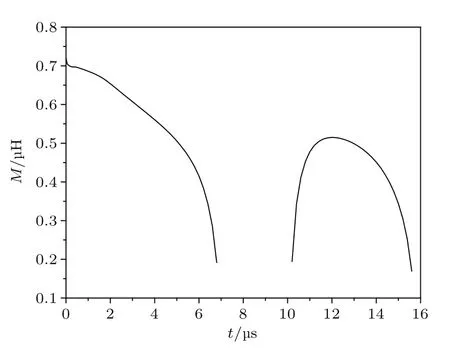
圖15 激勵線圈與等離子體之間的互感MFig.15.Mutual inductance M between plasma load and drive-coil.

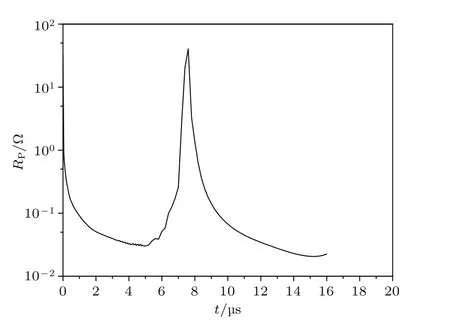
圖16 等離子體等效總電阻RPFig.16.Effective plasma total resistance RP.

綜上所述,耦合等離子體負載將驅動電路總體電阻增大,電感減小;等離子體與驅動電路的耦合作用強度隨等離子體瞬態參數分布及電路放電狀態的變化而變化;當等離子體電流在激勵線圈附近集聚時,M將增大,反之減小.

5 結 論

建立了一種耦合外部電路的磁流體力學模型,實現了對加速通道內等離子體二維流場結構演化過程及驅動電路放電過程的同步耦合求解.數值仿真成功復現了PIT的工作物理圖景,計算結果與實驗數據基本一致,借助這一新模型,實現了對電路-等離子體雙向耦合作用的定量分析.模型可用于研究PIT的工作原理,預測其推進性能,為推力器結構設計、參數優化提供技術支持和可行的計算方法.

[1]Polzin K A 2011J.Prop.Power27 3

[2]Martin A K,Dominguez A,Eskridge R H 201534th International Electric Propulsion ConferenceHyogo-Kobe,Japan,July 4–10,2015 p50

[3]Russell D,Poylio J H,Goldstein W 2004Space Conference and ExhibitSan Diego,America,September 28–30,2004 p6054

[4]Dailey C L,Loveberg R H 1987Pulsed Inductive Thruster Component TechnologyAFAL TR 07 012

[5]Dailey C L,Loveberg R H 1989AIAA/ASME/SAE/ASEE 25th Joint Propulsion ConferenceMonterey,America,July 10–12,1989 p2266

[6]Dailey C L,Lovberg R H 1993The PIT MkV Pulsed Inductive ThrusterNASA CR 19 1155

[7]Polzin K A,Choueiri E Y 2006IEEE Trans.Plasma Sci.34 3

[8]Polzin K A 2006Ph.D.Dissertation(Princeton:Princeton University)

[9]Polzin K A,Sankaran K,Ritchie A G,Reneau J P 2013J.Phys.D:Appl.Phys.46 475201

[10]Martin A K 2016J.Phys.D:Appl.Phys.49 025201

[11]Che B X 2015M.S.Thesis(Changsha:National University of Defense Technology)(in Chinese)[車碧軒2015碩士學位論文(長沙:國防科技大學)]

[12]Mikellides P G,Neilly C 2007J.Prop.Power23 51

[13]Mikellides P G,Ratnayake N 2007J.Prop.Power23 854

[14]Mikellides P G,Villarreal J K 2007J.Appl.Phys.102 103301

[15]Cheng Y G,Xia G Q 2017Acta Phys.Sin.66 075204(in Chinese)[成玉國,夏廣慶 2017物理學報 66 075204]

[16]Cheng Y G 2015Ph.D.Dissertation(Changsha:National University of Defense Technology)(in Chinese)[成玉國2015博士學位論文(長沙:國防科技大學)]

[17]ComsolMultiphysicsUsersGuide,Onlinevailable http://www comsol com/plasma-module/[2017-5-11]

[18]Li M,Liu H,Ning Z X 2015IEEE Trans.Plasma Sci.43 12

[19]John D A(translated by Yang Y)2011Hypersonic and High-Temperature Gas Dynamics(2nd Ed.)(Beijing:Aviation Industry Press)pp421–422(in Chinese)[小約翰D A著(楊永譯)2011高超聲速和高溫氣體動力學(第二版)(北京:航空工業出版社)第421—422頁]

[20]Cheng X 2009Thermal Plasma Heat Transfer and Flow(Bejiing:Science Press)pp50–55(in Chinese)[陳熙 2009熱等離子體傳熱與流動(北京:科學出版社)第50—55頁]

[21]Deb P,Agarwal R K 2001AIAA Aerospace Sciemces Meeting&ExhibitReno,America 2001,p794

[22]Tian Z Y 2008Ph.D.Dissertation(Changsha:National University of Defense Technology)(in Chinese)[田正雨2008博士學位論文(長沙:國防科學技術大學)]

[23]Ahangar M,Ebrahimi R,Shams M 2014Acta Astronaut.103 129

[24]Heiermann J 2002Ph.D.Dissertation(Stuttgart:Universitat Stuttgart)

[25]Sankaran K 2005Ph.D.Dissertation(Princeton:Princeton University)

[26]Glumb R J,Krier H 1986AIAA J.24 1331

[27]Lovberg R H,Dailey C L 1982AIAA/JSASS/DGLR 16th International Electric Propulsion ConferenceNew Orleans,America,November 17–19,1982 p1921

[28]Lovberg R H,Dailey C L 1982AIAA J.20 971