基于第一性原理分子動力學的填充方鈷礦熱輸運性質及微觀過程的研究?

王彥成 邱吳劼 楊宏亮 席麗麗 楊炯 張文清

1)(中國科學院上海硅酸鹽研究所,高性能陶瓷和超微結構國家重點實驗室,上海 200050)

2)(中國科學院大學,北京 100049)

3)(上海大學材料基因組工程研究院,上海 200444)

1 引 言

熱電材料需要優異的電輸運性質和低熱導率.理解低晶格熱導率的形成機理,對于提高熱電材料的性能非常重要[1].方鈷礦材料具有良好的電輸運性能,而且其內部特殊的籠狀結構能夠容納外來原子(填充原子),進而降低材料的晶格熱導率.因此,填充方鈷礦體系是一類在中溫區熱電性能十分優異的材料.再考慮到其不含鉛、碲等有毒元素的特點,在過去的十多年里,方鈷礦材料受到了研究人員的廣泛關注和研究[2?4],其性能也得到了大幅提升,尤其是以三元填充化合物為代表[5?7],熱電優值在800—850 K范圍達到了1.7—1.9.

然而在填充原子降低晶格熱導率的機理上,理論研究卻長期存在著爭論.傳統的觀點認為,填充原子與框架間較弱的化學鍵使其做類似于Einstein模式的大幅度獨立振動,并通過共振散射低頻的晶格聲子來降低晶格熱導率[8,9].一般來說,局域振動模式對材料自身性質所產生的影響,許多能夠在實驗上測得并在理論計算中得到一定程度的驗證[10].填充原子的這種特殊的振動行為則在非彈性中子散射和熱容測量的實驗研究中得到了確認[11?13].但另一方面,第一性原理計算表明填充原子與晶格框架存在著非簡諧的耦合[14],(La,Ce)Fe4Sb12的中子散射實驗結果也支持這一觀點,并認為填充原子與框架之間的作用似乎可以用聲子與聲子作用來描述,即將填充原子的振動描述為具有長程相干性和周期性特征的聲子行為[15].Li和Mingo[16]用第一性原理方法在三聲子框架下計算了全填體系YbFe4Sb12的聲子輸運性質,認為填充方鈷礦和其他常規材料一樣,填充原子的引入增強了三聲子的散射截面,因此降低了晶格熱導率,但其晶格熱導率的計算結果卻遠低于實驗值.以上的研究結果都表明了填充原子與晶格之間相互作用的復雜性,而這種復雜性與填充原子偏離平衡位置的大幅度振動行為密切相關.最近,在具有化學鍵層級特征的Cu3SbSe3化合物的研究[17,18]中發現,與周圍環境的成鍵較弱的部分,Cu原子會出現類似于非晶材料中協同特征明顯的低頻振動,其理論描述偏離了以晶態為基礎的“小參數”微擾近似.雖然在填充方鈷礦體系中填充原子處在封閉的籠子中,但是其同樣具有弱化學鍵下的動態漲落的亞晶格特征.因此,我們初步認為填充原子的振動行為偏離了微擾近似的圖像,相應地散射機理也可能同時存在非微擾的特征[18].本文要解決的關鍵問題是填充原子的運動是否偏離了微擾近似的范疇,并是否具有超出三聲子過程的散射機理,以及極低晶格熱導率的形成原因.

在半導體和絕緣體中,材料本征的晶格熱導率取決于其內部的聲子及其散射過程,可由聲子的玻爾茲曼輸運方程(Boltzmann transport equation)描述.基于零溫的第一性原理方法計算并預測材料晶格熱導率的準確程度,受到原子間作用力的計算和非彈性聲子散射機理選取的雙重影響[19].不同于利用凍聲子法[20,21]得到簡諧及非諧力常數的常規手段,本文采用考慮了有限溫度效應的第一性原理分子動力學(ab initiomolecular dynamics,AIMD)的方法,覆蓋了填充原子全部的相互作用,即充分考慮“全”相互作用的力常數.本文以YbFe4Sb12為例模擬填充原子這種大幅偏離平衡位置的振動行為,并捕捉得到其更為接近真實情況的軌跡與受力信息.AIMD的結果結合Hellman等[22,23]最近發展的溫度相關有效勢場(temperature-dependent effective potential,TDEP)方法,統計其動力學軌跡和相應的原子受力信息,擬合得到有效的二階、三階力常數.這實質上是將填充原子的作用等效為非諧作用進行考慮.在聲子非彈性散射方面,仍以三聲子過程為主要散射機理,計算聲子自能與壽命,以及晶格熱導率.通常情況下,這種做法在非諧作用較強的材料中符合較好,但是對于可能存在的非微擾的散射機理卻難以給予恰當的過程描述和機理解釋.從反證的角度來講,將計算得到的晶格熱導率和實驗結果相比較,進而檢驗填充原子引入的散射機理是否具有非微擾的特征,則可以為解釋相關體系熱導率降低的機理提供清晰的線索.因此,為了突出填充原子在熱輸運微觀過程的影響,選用Yb原子對方鈷礦進行填充.由于滿填體系具有最好的空間對稱性和最少的計算量,且CoSb3存在填充量上限我們選用YbFe4Sb12進行研究.

2 計算方法

非諧作用是聲子與聲子碰撞散射的主要原因,它會使聲子的頻率發生變化,而且峰也會產生一定的展寬,后者意味著聲子存在著有限的壽命.晶體的勢能展開形式可以寫為

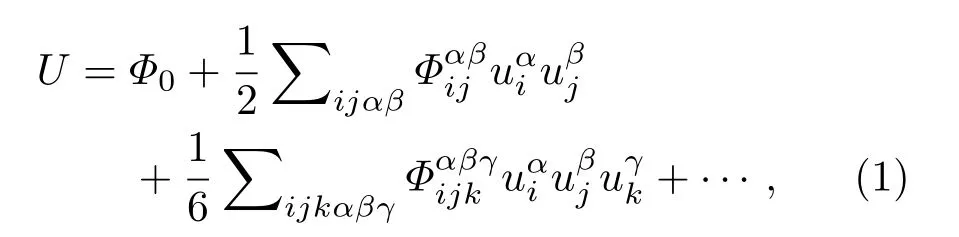
其中,Φ0為勢能的常數項;ui分別為原子i的位移;αβγ為笛卡爾分量的指標;表示二階與三階力常數;(1)式中右邊的第二、三項分別為簡諧勢與立方非諧勢,記為U2與U3.其中立方非諧勢的二次量子化形式可以寫作三聲子碰撞的形式,

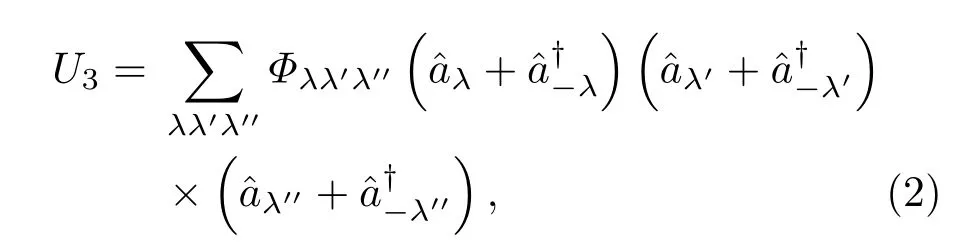
這里λ=(q,j),?λ=(?q,j),其中q,j分別為聲子模式的波矢和所在格波數,?a?λ和?aλ為聲子模式λ的增加和湮沒算符.Φλλ′λ′′為參與散射的三個聲子λ,λ′與λ′′間的作用強度,其表達式[24,25]為

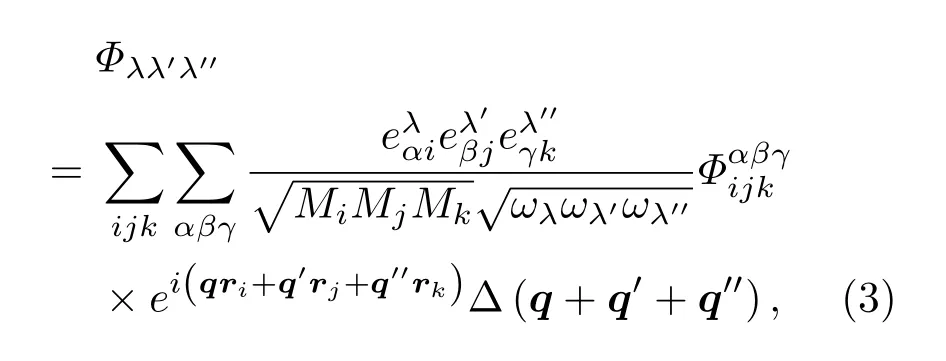
這里的?(q+q′+q′′)表達的是準動量守恒條件,即當q+q′+q′′為0或者等于倒格矢G的整數倍時取1,否則取0.在微擾理論下,考慮三聲子過程為一階近似,利用Fermi’s golden rule[24]得到聲子模式λ的自能虛部項Γλ(ω),

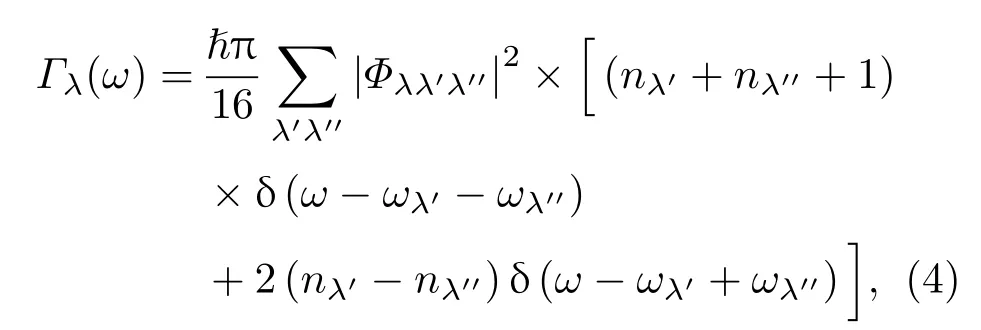
其中,nλ為平衡態時聲子的占據數.利用聲子壽命和聲子展寬2Γλ(ω)的關系,τλ(ω)=1/2Γλ(ω),可以計算得到晶格熱導率其中,Cλ為摩爾熱容.

采用基于密度泛函理論的平面波基矢軟件VASP軟件包進行第一性原理分子動力學的模擬,采用綴加平面波的方法,交換關聯勢采取廣義梯度近似(GGA)下的Perdew-Burker-Ernzerhof形式,平面波截斷能為300 eV,在正則系綜下模擬了YbFe4Sb12的2×2×2(272個原子)超胞在300,400,500和600 K等溫度下的動力學過程,其中溫度控制采取了Nosé thermostat的熱浴,布里淵區積分僅限于Γ點,在系統達到平衡狀態后模擬時間在30 ps以上,模擬時間步長為2 fs.為考慮熱膨脹的因素,不同溫度下YbFe4Sb12的晶胞常數采用了quasi-harmonic approximation(QHA)方法進行估算,所用的軟件為phonopy[20].使用TDEP軟件[22,23]對AIMD中原子的軌跡與受力進行最小二乘法擬合,進而得到二階與三階力常數.該方法中考慮了平移不變性和晶格自身的對稱性,以減少力常數矩陣中所需擬合的獨立矩陣元數目,進而減少了計算量.在計算中,取二階力常數的截斷半徑大致為10 ?,三階力常數的截斷半徑為5.0 ?.這是由于通常情況下三階力常數比較小[26],只需考慮較為鄰近的三原子對的受力情況即可.在二階和三階力常數的基礎上,采用11×11×11的q點網格來計算YbFe4Sb12的聲子壽命以及晶格熱導率等熱輸運性質.

3 結果與討論

所用AIMD模擬結合TDEP的方法的特點,能夠從更趨實際的原子運動軌跡中統計分析出材料的力常數等內在性質.高溫下材料內部原子大幅振動,并帶來顯著的非諧效應等,是這一方法的長處所在[23].而在低溫或者材料內原子位移參數(atomic displacement parameters,ADP)比較小的情況下,該方法和凍聲子法的圖像趨向一致.

方鈷礦材料最顯著的特點是框架部分與填充原子在振動幅度存在著較大的差別,框架原子主要是圍繞著平衡位置附近做較小的振動,而填充原子的振動幅度是前者的3—5倍之多.在討論填充體系YbFe4Sb12之前,用AIMD結合TDEP方法計算純方鈷礦Co4Sb12的熱輸運性質,來檢驗這一方法的有效性與準確性.

3.1 純方鈷礦材料Co4Sb12的聲子輸運性質

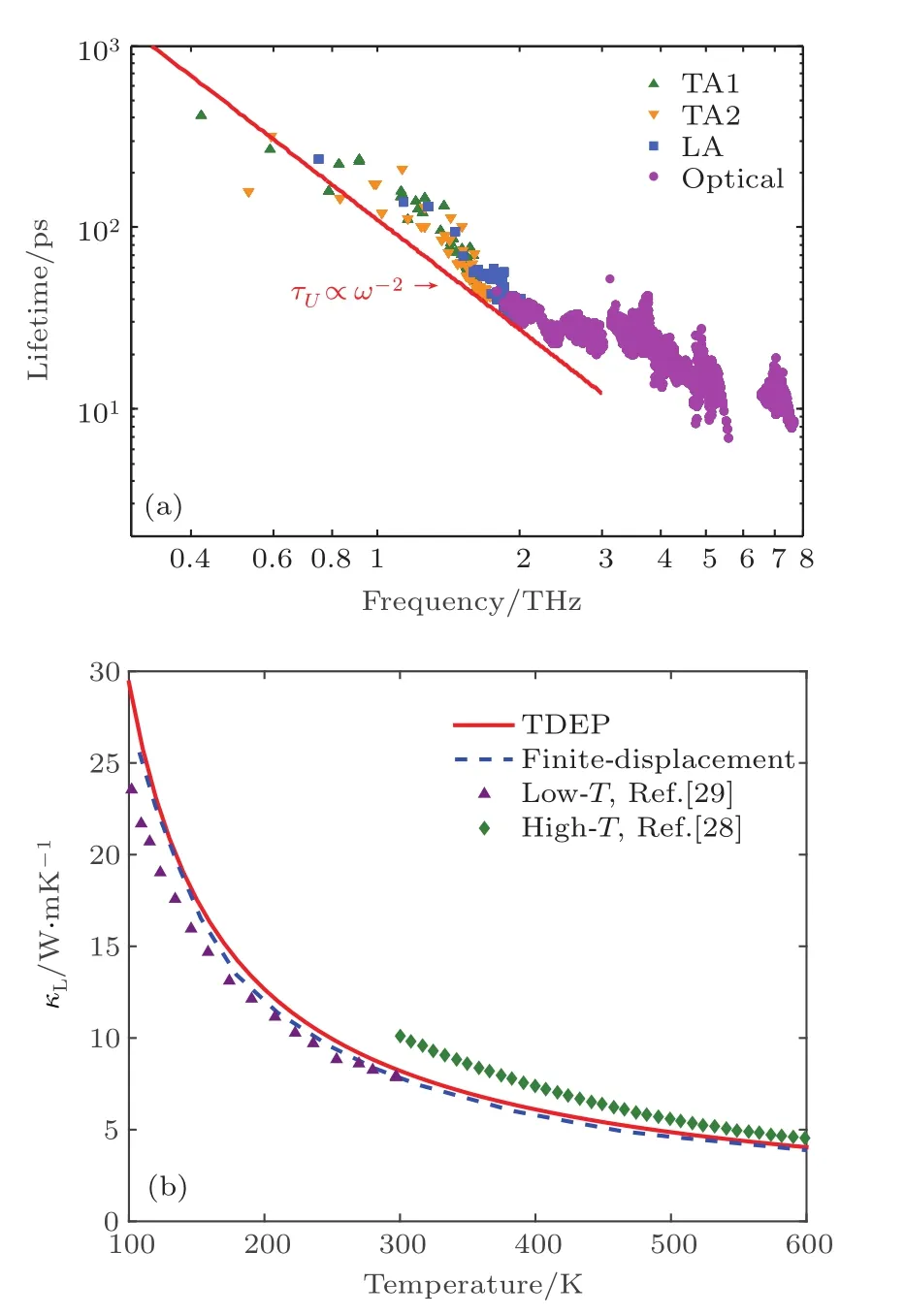
圖1 使用TDEP方法計算的Co4Sb12(a)在300 K的聲子壽命隨頻率變化的關系,(b)晶格熱導率 κL的溫度依賴關系(紅線),其中低溫和高溫實驗晶格熱導率分別來自Nolas等[29]和Chen等[28]的研究,作為對照的凍聲子法計算的κL(藍色虛線)來自于Guo等[30]的研究.Fig.1.(a)Phonon lifetimes of Co4Sb12at 300 K vs.frequency and(b)its lattice thermal conductivity vs.temperature,calculated by TDEP(red solid line).The experimental data of κLat low and high temperature is from references of Nolas et al.[29]and Chen et al.[28]respectively.The referent calculated κLby fi nite-displacement approach(blue dash line)is from reference of Guo et al.[30].

用AIMD模擬300 K時Co4Sb12的動力學行為,并用TDEP擬合得到其二階與三階力常數,計算得到了聲子壽命和晶格熱導率的結果,如圖1所示.從圖1(a)中可以看出Co4Sb12的聲子壽命τλ(ω)正比于ω?2.通常來說,非諧作用所帶來的聲子非彈性散射機理主要為三聲子U過程,其聲子壽命的表達式具有τU∝ω?2的關系[27].這一結果表明了在純方鈷礦Co4Sb12中,三聲子過程是其主要的散射機理.因此,在三聲子框架下計算得到的晶格熱導率同實驗結果[28,29]符合得比較好,而且該結果與Guo等[30]用凍聲子方法計算的結果(GGA potential的結果)幾乎一致,見圖1(b).這說明用AIMD模擬結合TDEP方法計算材料熱輸運性質,確實是有效可行的.

3.2 全填體系YbFe4Sb12的聲子輸運性質

不同于純方鈷礦材料Co4Sb12僅用三聲子相互作用就能計算得到較為準確的熱導率結果,填充原子的引入使得體系的熱導計算變得復雜起來.為研究填充原子對于方鈷礦材料熱輸運性質的影響,計算了YbFe4Sb12在300 K時的聲子壽命的頻率變化關系,并分析了填充原子振動模式的局域性特征,以及這些模式在壽命上所具有的特點.從圖2(b)中可以看到,相比于純的體系Co4Sb12,YbFe4Sb12的聲子壽命整體降低了許多,這表明后者的非諧作用比純的體系增強了很多.其中低頻的聲學支模式和部分光學支模式的壽命滿足ω?2的關系,但是在填充原子振動頻率附近的模式,其壽命相比τU∝ω?2趨勢有著顯著的降低.考慮到TDEP方法仍是在微擾近似的前提下,以三聲子過程為主要框架來計算聲子輸運性質的這一特點,我們認為這是由于填充原子的引入帶來了非常規的聲子散射機理所致.

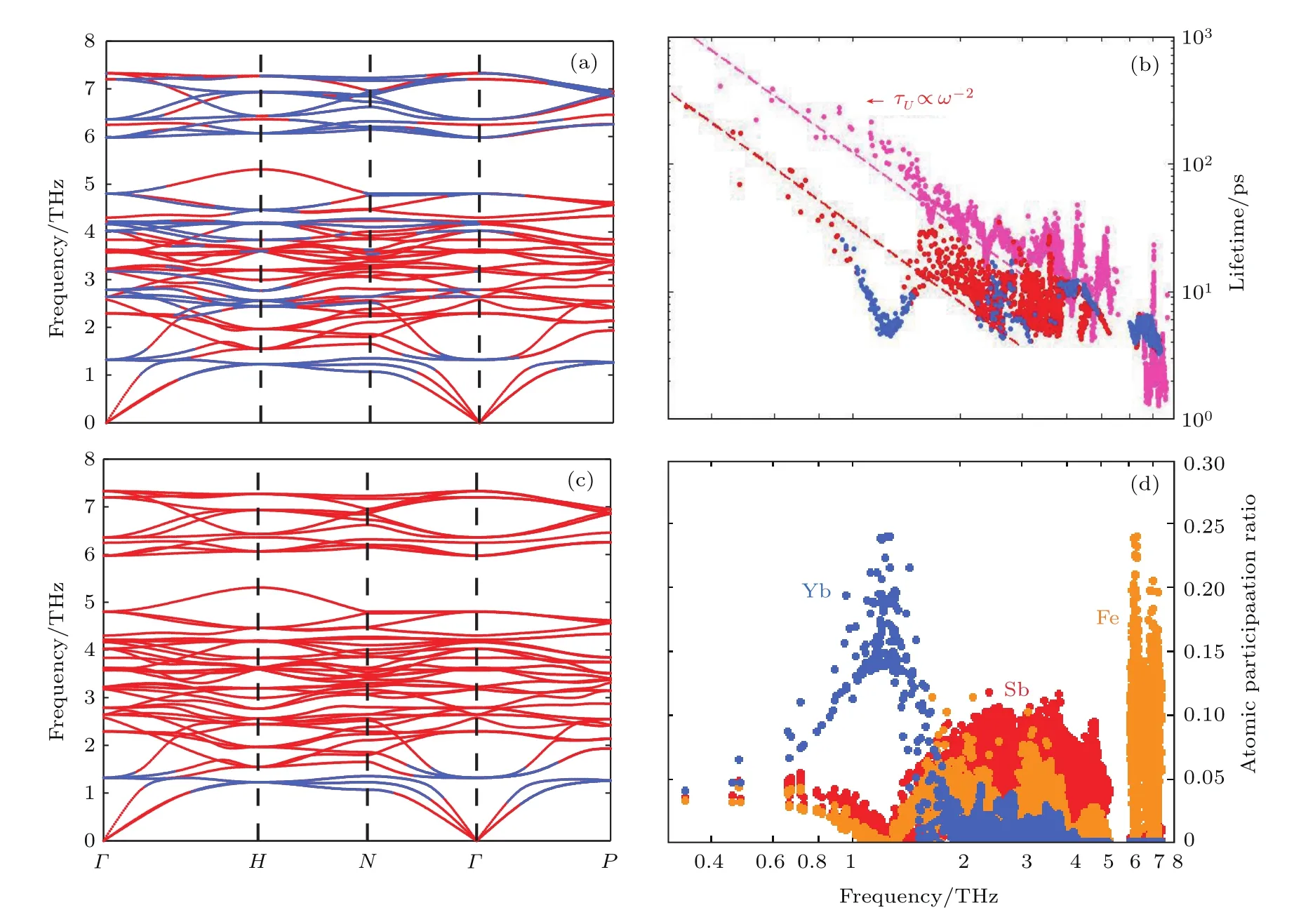
圖2 YbFe4Sb12的聲子色散關系(a),(c)和聲子壽命的頻率變化關系(b),以及不同頻率的原子參與率APR分布(d),其中(a)和(b)中的藍色部分為聲子參與率PR＜0.2部分,紅色部分為PR＞0.2部分,(b)中粉紅色點為Co4Sb12的聲子壽命,(b)中虛線為擬合得到的各自顏色部分的頻率變化趨勢,均為ω?2關系,(c)中藍色部分為填充原子APR(Yb)＞0.1的部分Fig.2.Calculated phonon dispersions of YbFe4Sb12(left),its phonon lifetimes(b)and atomic participation ratio for phonon modes of YbFe4Sb12(d).Blue parts of top panels(a),(b)mean modes with low PR(PR＜0.2).In panel(b)pink dots are phonon lifetimes of Co4Sb12,while red(PR＞0.2)and blue dots(PR＜0.2)are lifetimes of YbFe4Sb12,and dash lines are fi tted ω?2trends of lifetimes for U process.In panel(c),blue part means phonon modes with high APR of Yb,which is larger than 0.1.

為分析這部分振動模式的性質及其與Yb的關系,計算了聲子參與率p(ωλ)(participation ratio,PR)和原子參與率pi(ωλ)(atomic participation ratio,APR),它們分別描述了所有原子在聲子模式λ中的參與程度[31]與不同原子i對于聲子模式λ的貢獻[32],其公式如下:

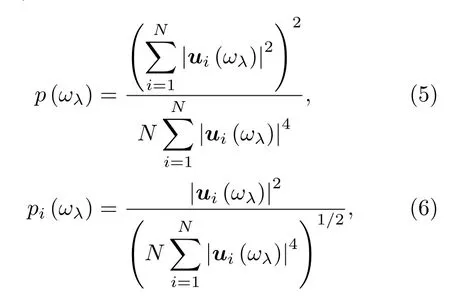
圖2(b)中偏離τU∝ω?2關系的振動模式,其PR值恰好小于0.2,可知這部分模式為局域振動模式.這些低頻局域模式的波矢分布可參見圖2(a)中 0—2 THz范圍內的藍色部分.而原子參與率APR的分析能夠幫助我們找到這些局域模式中的主要參與原子.圖2(d)中0.8—1.4 THz范圍內Yb的參與率要遠高于框架原子Fe和Sb,這一頻率范圍又和圖2(b)中的低頻局域振動模重合,其波矢分布(圖2(c)中藍色部分)與圖2(a)中局域振動模式的低頻部分一致.這些表明填充原子Yb的振動屬于分布在較大的波矢區間內的低頻局域振動模.因此可以認為聲子壽命偏離ω?2關系所對應的散射機理,實際是由填充原子Yb主導的局域振動模式參與的聲子散射過程.這一物理過程的實質是在材料內部傳播的晶格聲子,借助填充原子與局域振動模發生不停的轉換,而這種振動特征的變換,正是除去較強非諧作用之外填充方鈷礦材料熱阻的主要來源.這種相似的結論在Pailhès等[32]的研究中也有所體現.因此,鑒于填充原子Yb的局域振動特點,其對于晶格框架的影響原則上可以近似認為具有累加的特點,即當Yb的填充量減小時,填充體系的非諧作用以及非常規的聲子散射均會減弱.實驗上填充體系晶格熱導率隨填充量增加而降低[34],也印證了這一點.

從以上討論中,我們對填充原子帶來的散射機理有了較為初步的整體了解.接下來從細節的角度來驗證這一論斷,并分析填充原子在低熱導率成因中所起的具體作用.通常來講,非諧作用對于材料聲子譜的影響,主要表現在聲子的峰位和半高寬,峰位的變化即為頻率的位移,展寬則表明存在著聲子的阻尼,意味著其有限的聲子壽命.這分別對應著聲子自能Σ(?)=?(?)+iΓ(?)中的實部?與虛部Γ,其中?=E/?,E為中子的探測能量,這些都可以在聲子的中子散射截面σλ(?)中得到比較直觀的反映.其公式[35]寫作

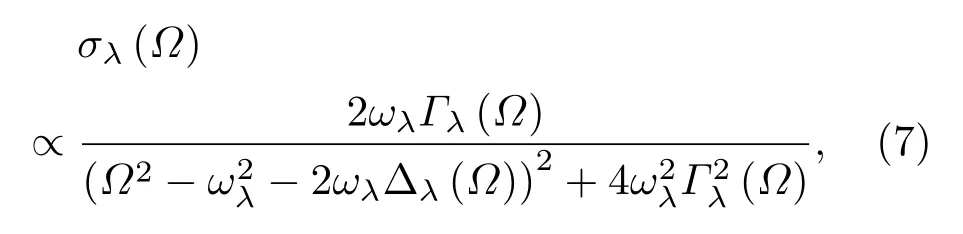
其中ωλ為聲子模式λ的本征頻率.

圖3(a)為Γ-P方向中子散射截面的計算結果.聲子模式振動特征的分析,顯示出YbFe4Sb12的低頻聲子具有類似于clathrate的avoid crossing[36]的特征,如圖3(a)中標識的橫光學支TO/TO′,與縱聲學支LA/LA′,在其相互臨近的區域(Q3點附近)產生作用,然后彼此分開(即為TO′與LA′部分).可以看出TO/TO′的展寬都比較大,相應地壽命都比較小.從圖2的結論中,我們了解到這部分振動模式中Yb的貢獻很大,通過分析振動模式中Yb原子的權重定量地得到了在avoid crossing前后部分TO/TO′,以及LA/LA′中填充原子Yb在聲子展寬上的具體貢獻,如圖3(b)和圖3(c)所示.可以看到,Q1,Q2,Q4和Q5處TO/TO′中Yb所貢獻的展寬較為一致,且都很高,這說明Yb的振動模式壽命比較低.而在Q3處,由于相互作用,TO中的Yb的振動有一部分轉移到了LA中,提高了LA的展寬.如果將Q3處TO與LA展寬中Yb的貢獻量加起來,得到的Yb振動模式的展寬同avoid crossing前后Q1,Q2,Q4和Q5處也保持相近的水平.這說明填充原子Yb的振動模式自身展寬比較大,壽命很低,而與之發生相互作用的聲學支聲子由于混入了低弛豫時間的填充原子Yb的振動,其壽命也隨之降低.這種圖像與填充原子Yb局域振動模參與的非常規的三聲子過程,令這部分模式的壽命比ω?2關系更低的結果是相近的,也能夠部分地解釋晶格熱導率降低的原因.

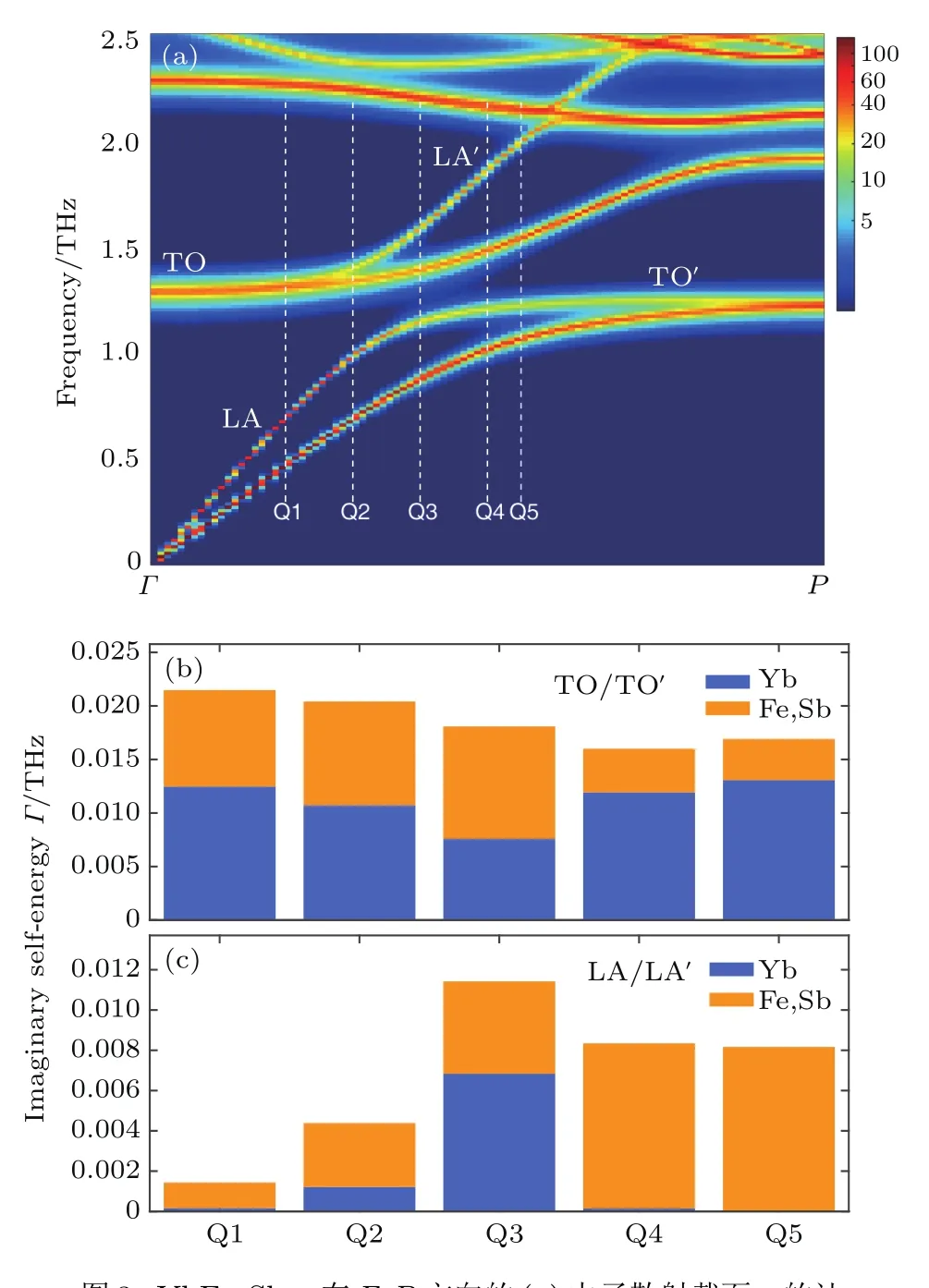
圖3 YbFe4Sb12在Γ-P方向的(a)中子散射截面σ的計算結果,其中顏色表示峰的強度;(b)橫光學支TO/TO′;(c)縱聲學支LA/LA′在avoid crossing前后部分的聲子自能虛部Γ;(b)和(c)中Q1—Q5對應(a)中白色虛線標識的5個波矢,藍色和橘色分別對應Yb和框架原子Fe/Sb各自的貢獻量Fig.3. (a)Calculated scattering cross section of YbFe4Sb12along Γ-P direction.Intensities is plotted on a logarithmic scale.Imaginary self energy Γ (ω)of TO/TO′branch(b)and LA/LA′branch(c)at Q1–Q5 wave vector points around the avoid crossing part,which are labeled in panel(a).In panels(b)and(c),blue and orange parts mean contributions of Yb and Fe/Sb atoms to Γ (ω)respectively.

3.3 動力學上填充原子的局域振動特征

以上討論均是從晶格動力學的角度出發,以聲子以及聲子與聲子相互作用為前提,即將晶體材料中原子的振動簡化為聲子這一集體振動的元激發行為.雖然前面的討論中,確定了填充原子Yb的振動模式具有局域振動的特征,但是填充原子之間的在振動行為上的關聯性質,以及是否適用于聲子的圖像,仍舊沒有確切的結論.而這又是回答填充原子以何種方式與框架原子或晶格聲子作用的物理圖像上關鍵的基礎問題.

我們從動力學的角度出發,分析填充原子與周圍框架原子在微觀運動過程中的關聯性質,力求為理解其相互作用構建一個清晰而準確的物理圖像.研究中引入了原子速度的相干性這一物理量,它實際上是歸一化的原子速度的互關聯譜.可以將原子對中的兩個原子的速度理解為兩個或隨機或存在著某種程度線性關系的信號,它們在特定頻率上的關聯性質可以用互關聯譜

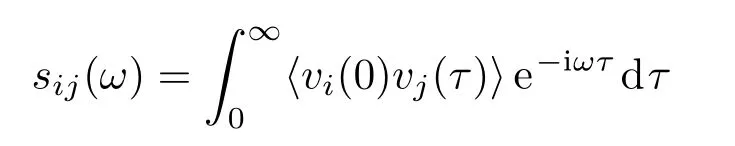
來表示.借助于和卷積相似的數學手段,除下原子i或j的速度自關聯函數的功率譜sii(ω)或sjj(ω),得到歸一化后的互關聯譜,

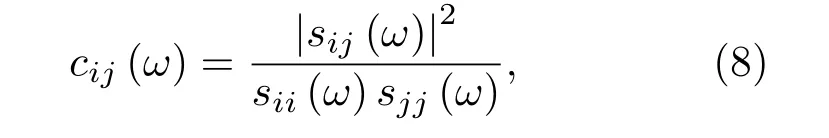
這里稱cij(ω)為原子i和j速度在頻率ω上的相干性;cij(ω)是一無量綱的數,取值范圍為0≤cij(ω)≤ 1. 當cij(ω)≈1.0時,vi(t)和vj(t)是線性相關的;當cij(ω)≈0時,vi(t)和vj(t)彼此之間是相互獨立和隨機的關系.

圖4是分析YbFe4Sb12在600 K時AIMD的數據得到的填充原子Yb和框架原子Fe/Sb之間的速度關聯性質的結果,其中原子對中原子的距離選為9.2 ?,即為晶胞Yb2Fe8Sb24的周期長度.從YbFe4Sb12的聲子分波態密度的結果中可知填充原子Yb振動模式的頻率范圍在1—1.3 THz,Sb原子的振動頻率主要在1—5 THz,Fe的振動頻率主要為6—7.5 THz.由圖4可以看到,在1—1.3 THz的特征振動頻率范圍內,原子對Yb-Yb的相干性小于0.1,可知其關聯性非常弱.而框架原子Sb-Sb和Fe-Fe的在其特征振動頻率范圍的相干性均在0.35左右,其關聯性比Yb要強很多.鑒于框架原子Fe/Sb這種具有關聯性的運動,通常被解釋為具有周期性和集體振動等元激發特征的晶格聲子,基本可以認為填充原子Yb這種關聯性較弱且周期性不明顯的運動偏離了聲子的圖像,更傾向于彼此間相互獨立的局域振動.有了這一認識,再將填充原子和框架部分的晶格聲子間的作用解釋為三聲子過程則是不合適的.前面部分中用TDEP的三聲子框架來計算聲子輸運性質,可以視作一種等效的處理,而等效的效果如何,則可以從其晶格熱導率的計算結果直觀地看出來.

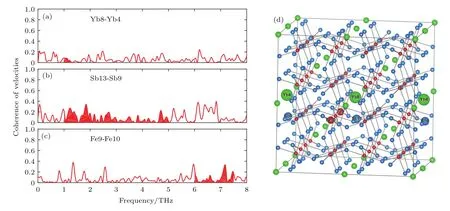
圖4 在600 K時YbFe4Sb12中不同種類原子對(a)Yb-Yb,(b)Sb-Sb,(c)Fe-Fe的原子速度相關性.為方便查看,各自原子主要貢獻的振動頻率范圍由紅色填充作為標識,且原子對中的原子編號在圖(d)中均有標明,其彼此間的距離均為9.2 ?Fig.4.Coherence of velocities between pairs of atoms in YbFe4Sb12at 600 K:(a)Yb-Yb,(b)Sb-Sb,(c)Fe-Fe,and numbers behind atom name are index of these atoms in the supercell.As a guide to see,the portion under curves within the range of vibration frequency dominated by each element is fi lled with red color.Distances between pairs of atoms in(a)–(c)labeled in panel(d)are both 9.2 ?.

3.4 YbFe4Sb12晶格熱導率的計算與修正

如圖5所示,在YbFe4Sb12的晶格熱導率的計算上做了以下的幾點嘗試.首先用300 K時的二階和三階力常數,計算得到的晶格熱導率隨溫度變化的關系,不出意料地滿足T?1的規律,這是其散射機理以三聲子過程為主所決定的.然后,考慮填充原子作用可能受溫度的影響,我們通過AIMD和TDEP方法得到了300—600 K幾個不同溫度下的力常數,在三聲子框架下分別計算得到各自溫度下的晶格熱導率.可以看到其溫度依賴關系不再為T?1的關系,變得和實驗數據的趨勢有些接近,這說明考慮溫度對于非諧或者填充原子作用的影響的思路是對的.但是在數值上,采用不同溫度力常數得到的結果與實驗結果仍然存在著一定的差距.結合動力學上原子關聯性討論的結果,我們認為這種差距的原因在于三聲子散射過程的圖像不適用于填充原子與晶格聲子的相互作用.

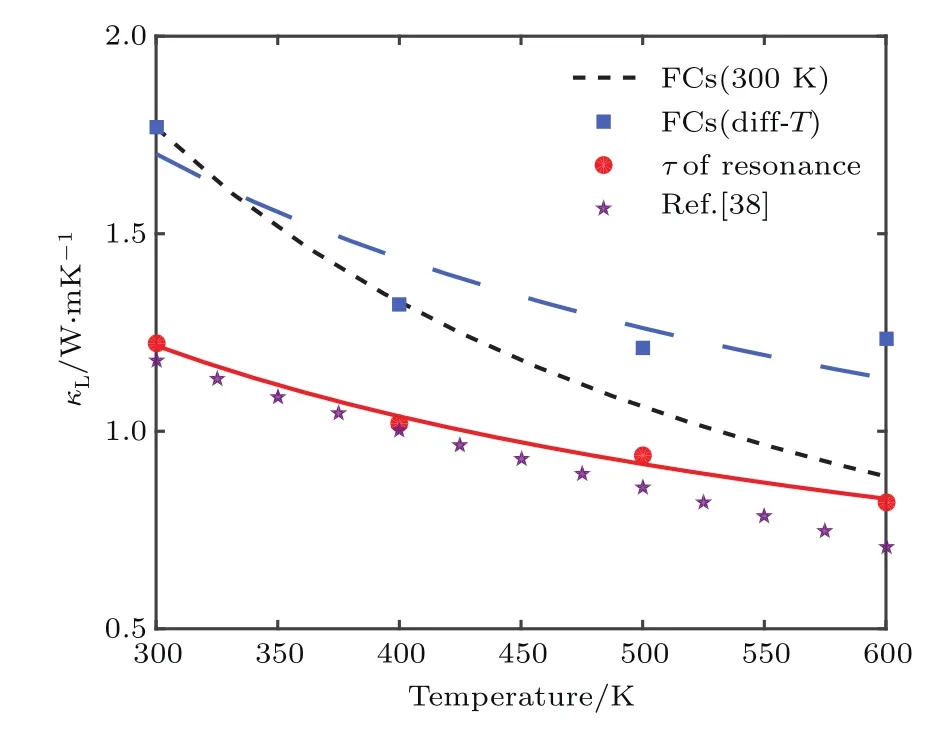
圖5 用TDEP方法計算得到的YbFe4Sb12晶格熱導率κL結果.黑色虛線為300 K的單一力常數的計算結果,藍色方塊為不同溫度下力常數計算得到的κL,紅色圓點為Yb振動模式壽命經過共振散射修正后所得到的κL,紫色五角星為YbFe4Sb12的實驗晶格熱導率結果,藍色、紅色線為各自數據擬合所得趨勢線Fig.5.Calculated lattice thermal conductivity κLof YbFe4Sb12vs.temperature through TDEP method.Black dash line is the calculated κLwith 2nd/3rdforce constants at 300 K and is proportional to 1/T.Blue squares are κLof 300–600 K calculated by 2nd/3rd force constants at each temperature.Red dots are κL got by modi fi ed lifetimes of Yb-dominant modes by resonant scattering form.Blue dash line and red solid line are fi tted by the data of blue squares and red dots respectively.Purple pentagrams are experimental κL of YbFe4Sb12from Ref.[38].

前面關于填充原子Yb的振動與聲學支聲子耦合,并降低其壽命的表述,也適合于共振散射的解釋.用共振散射的壽命形式[37],即

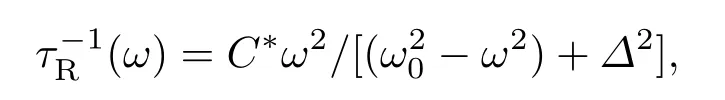
作為由Yb所主導的局域振動模式的壽命,其他模式的聲子壽命保持不變,代入到熱導率的計算中,即

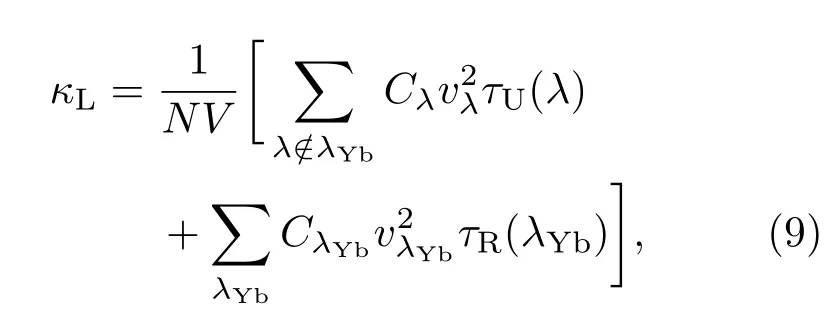
則可以將晶格熱導率大致降低到了和實驗結果[38]相近的水平.這說明了填充原子降低晶格熱導率的原因,需要用超出三聲子過程的非微擾的散射機理來解釋,而共振散射是其中的一種可能.

4 結 論

以全填充方鈷礦YbFe4Sb12為例,采用第一性原理分子動力學模擬(AIMD),并結合溫度相關有效勢場(TDEP)的方法研究了填充原子在熱輸運過程中的作用,發現填充原子Yb的振動模式具有強烈的局域特征,其降低晶格熱導率的機理超出了三聲子倒逆過程的范疇.由于AIMD充分考慮了有限溫度下填充原子與框架的相互作用,而TDEP方法將之納入到了等效的非諧力常數內.在此基礎上計算得到的聲子輸運性質表明,Yb局域振動模式通過與聲學支耦合,確實大幅降低了聲學支模式的壽命,但是將之作為三聲子倒逆過程考慮,理論計算的晶格熱導和實驗結果存在著嚴重的偏離.而且動力學過程中原子運動的關聯性質分析表明,填充原子Yb的運動存在明確的局域和獨立特征,不符合聲子周期性的集體振動圖像,所以填充原子散射晶格聲子、貢獻熱阻的機理具有超出傳統三聲子框架的特征.將填充原子Yb局域振動模式的壽命做共振散射的修正,可以將晶格熱導率的計算結果降到和實驗相符的水平.因此,在類似于Yb原子填充體系中,即在填充方鈷礦體系中存在強烈且孤立的局域振動模時,填充原子的局域振動通過與聲學支聲子耦合,以共振散射為主、聲子間相互作用為輔的形式大幅降低傳熱聲子的壽命,進而降低了材料的晶格熱導率.

[1]Shi X,Xi L L,Yang J,Zhang W Q,Chen L D 2011Physics40 710(in Chinese)[史迅,席麗麗,楊炯,張文清,陳立東2011物理40 710]

[2]Nolas G S,Morelli D T,Tritt T M 1999Annu.Rev.Mater.Sci.29 89

[3]Shi X,Bai S,Xi L,Yang J,Zhang W,Chen L,Yang J 2011J.Mater.Res.26 1745

[4]Rull-BravoM,MoureA,FernándezJF,Martín-González M 2015RSC Adv.5 41653

[5]Shi X,Yang J,Salvador J R,Chi M,Cho J Y,Wang H,Bai S,Yang J,Zhang W,Chen L 2011J.Am.Chem.Soc.133 7837

[6]Rogl G,Aabdin Z,Scha fl er E,Horky J,Setman D,Zehetbauer M,Kriegisch M,Eibl O,Grytsiv A,Bauer E 2012J.Alloys Compd.537 183

[7]Xi L L,Yang J,Shi X,Zhang W Q,Chen L D,Yang J H 2011Sci.China:Phys.Mech.Astron.41 706(in Chinese)[席麗麗,楊炯,史迅,張文清,陳立東,楊繼輝2011中國科學:物理學力學天文學41 706]

[8]Slack G A,Tsoukala V G 1994J.Appl.Phys.76 1665

[9]Nolas G,Cohn J,Slack G 1998Phys.Rev.B58 164

[10]Huang L F,Li Y L,Ni M Y,Wang X L,Zhang G R,Zeng Z 2009Acta Phys.Sin.58 306(in Chinese)[黃良鋒,李延齡,倪美燕,王賢龍,張國仁,曾雉 2009物理學報58 306]

[11]Keppens V,Mandrus D,Sales B C,Chakoumakos B C,Dai P,Coldea R,Maple M B,Gajewski D A,Freeman E J,Bennington S 1998Nature395 876

[12]Hermann R P,Jin R,Schweika W,Grandjean F,Mandrus D,Sales B C,Long G J 2003Phys.Rev.Lett.90 135505

[13]Dimitrov I K,Manley M E,Shapiro S M,Yang J,Zhang W,Chen L D,Jie Q,Ehlers G,Podlesnyak A,Camacho J,Li Q 2010Phys.Rev.B82 174301

[14]Feldman J L,Singh D J,Mazin I I,Mandrus D,Sales B C 2000Phys.Rev.B61 R9209

[15]Koza M M,Johnson M R,Viennois R,Mutka H,Girard L,Ravot D 2008Nat.Mater.7 805

[16]Li W,Mingo N 2015Phys.Rev.B91 144304

[17]Qiu W,Xi L,Wei P,Ke X,Yang J,Zhang W 2014Proc.Natl.Acad.Sci.USA111 15031

[18]Qiu W,Ke X,Xi L,Wu L,Yang J,Zhang W 2016Sci.China:Phys.Mech.Astron.59 627001

[19]Broido D A,Malorny M,Birner G,Mingo N,Stewart D A 2007Appl.Phys.Lett.91 231922

[20]Togo A,Oba F,Tanaka I 2008Phys.Rev.B78 134106

[21]Li W,Carrete J,A.Katcho N,Mingo N 2014Comput.Phys.Commun.185 1747

[22]Hellman O,Steneteg P,Abrikosov I A,Simak S I 2013Phys.Rev.B87 104111

[23]Hellman O,Abrikosov I A 2013Phys.Rev.B88 144301

[24]Srivastava G P 1990The Physics of Phonons(Boca Raton:CRC press)p88

[25]Hellman O,Broido D A 2014Phys.Rev.B90 134309

[26]Li C W,Hellman O,Ma J,May A F,Cao H B,Chen X,Christianson A D,Ehlers G,Singh D J,Sales B C,Delaire O 2014Phys.Rev.Lett.112 175501

[27]Slack G A,Galginaitis S 1964Phys.Rev.133 A253

[28]Chen L D,Kawahara T,Tang X F,Goto T,Hirai T,Dyck J S,Chen W,Uher C 2001J.Appl.Phys.90 1864

[29]Nolas G S,Fowler G,Yang J 2006J.Appl.Phys.100 043705

[30]Guo R,Wang X,Huang B 2015Sci.Rep.5 7806

[31]Hafner J,Krajci M 1993J.Phys.:Condens.Matter5 2489

[32]Pailhes S,Euchner H,Giordano V M,Debord R,Assy A,Gomes S,Bosak A,Machon D,Paschen S,de Boissieu M 2014Phys.Rev.Lett.113 025506

[33]Euchner H,Pailhès S,Nguyen L T K,Assmus W,Ritter F,Haghighirad A,Grin Y,Paschen S,de Boissieu M 2012Phys.Rev.B86 224303

[34]Zhao X Y,Shi X,Chen L D,Zhang W Q,Bai S Q,Pei Y Z,Li X Y,Goto T 2006Appl.Phys.Lett.89 092121

[35]Cowley R A 1968Rep.Prog.Phys.31 123

[36]Christensen M,Abrahamsen A B,Christensen N B,Juranyi F,Andersen N H,Lefmann K,Andreasson J,Bahl C R,Iversen B B 2008Nat.Mater.7 811

[37]Pohl R 1962Phys.Rev.Lett.8 481

[38]Qiu P F,Yang J,Liu R H,Shi X,Huang X Y,Snyder G J,Zhang W,Chen L D 2011J.Appl.Phys.109 063713