基于參數不確定性分析的SAR土壤水分反演精度控制方法

陳魯皖，韓 玲，王文娟，秦小寶

(長安大學 地質工程與測繪學院，陜西 西安 710064)

土壤水分，是全球氣候系統的核心變量之一[1]。對于地球表層的能量和水分平衡具有重要作用，土壤水分的時空分布與動態變化對陸地-大氣間熱量平衡、大氣環流產生顯著影響[2]。土壤水分的空間分布對于干旱檢測、農業生產和田間灌溉管理也具有極為重要的意義，尤其是在干旱半干旱的中國西北地區。對土壤水分進行動態、實時、大范圍和較高精度的估算，利用空間分辨率較高的微波遙感反演是較為有效的手段。

土壤水分反演過程中的不確定性分析是當前研究的熱點，E. De Keysera等[3]提出了一種基于線性回歸的粗糙度參數化方法，并使用概率分布對其不確定性進行估計，通過反演模型進一步的傳播不確定性，得到反演土壤水分的概率分布。J. FernA′ ndez-GA′ lvez等[4]認為大多數土壤水分反演方法依賴于土壤水分與介電特性之間的關系，比較了包含這種關系的9種反演模型，并對土壤水分和介電特性之間的不確定性引起的誤差進行量化。Ma C等[5]提出了一種基于貝葉斯定理和馬爾可夫鏈蒙特卡羅方法的土壤水分概率反演(PI)算法，能夠定量描述土壤水分反演的不確定性，通過最大似然估計得到高精度的土壤水分估計。李大治[6]通過集合反演來研究土壤水分反演過程中由觀測誤差、模型參數誤差以及不同的反演策略所引起的不確定性。verhoest等[7]研究發現，利用SAR進行土壤水分反演，地表粗糙度參數的不確定性是導致土壤水分反演誤差的重要來源。現有的不確定性研究大都集中在如何定量描述模型參數的不確定性，以及研究參數的不確定性對土壤水分反演結果不確定性的影響方面，而對于利用模型參數的不確定性來控制土壤水分反演結果的精度方面的研究較少。

本文首先對AIEM模型的主要參數進行敏感性分析，然后使用Rahman的LUT(look-up tables)方法[8]來反演土壤水分，研究AIEM模型主要影響參數的不確定性，然后基于參數不確定性計算得到不同入射角時滿足一定反演精度的主要影響參數的誤差控制范圍。在反演中使用LUT法計算有效相關長度(lmod)來代替實際測量值，可避免引入粗糙度參數測量過程中的不確定性[9]。根據不同程度的高斯噪聲對主要影響參數的取值進行隨機擾動，得到大量各參數采樣值，輸入AIEM模型中得到帶噪聲的后向散射系數集合；通過LUT方法反演得到Mv，計算得到反演結果的RMSE和標準方差，得到滿足一定反演精度的各影響參數的誤差量級控制范圍；研究得到不同入射角時滿足一定反演精度的各影響參數的誤差量級控制范圍。通過使用ENVISAT ASAR影像和同步地面觀測數據試驗驗證，證明本文得到的各影響參數的誤差量級控制范圍在較大的入射角范圍內都適用。

1 研究區與數據

地面試驗數據來源于中國科學院寒區旱區科學數據中心所提供的“黑河綜合遙感聯合試驗”。研究樣區位于甘肅省黑河中游的臨澤樣地，樣地較為平坦。臨澤地區氣候類型為大陸性荒漠草原氣候，年蒸發量1 830.4 mm，平均降水量118.4 mm，年平均氣溫7.7 ℃。選取了與2008-05-24、2008-07-11 ASAR影像同期的臨澤采樣區地面土壤水分觀測數據。

選用歐空局的ENVISAT-1衛星上ASAR傳感器獲取的SAR影像作為土壤含水量反演的數據源。采用了包含臨澤地區的2008-05-24、2008-07-11一共2幅ASAR數據，入射角θ范圍依次分別為(15.0°,22.9°)、(31.0°,36.3°)，經度范圍(99°28′E,101°24′E)，緯度范圍(38°42′N,40°03′N)，入射波段為C波段(f=5.331 GHZ)，地面分辨率為12.5 m×12.5 m，工作模式為Alternating Polarization，極化方式為VV和VH兩種見圖1。其中圖1(a)、圖1(b)分別為研究區的TM5、4、3假彩色合成影像和ASAR的VV極化影像(2008-07-11)。

2 研究方法

為了實現敏感性和不確定性的定量分析，通過幾個步驟進行研究：

1)對AIEM模型的各輸入參數進行全局敏感性分析，得到各主要參數對模型輸出后向散射系數的影響，確定各參數在模型中的貢獻大小；

2)對臨澤樣區的實測數據的取值范圍進行統計分析，得到AIEM模型輸入參數標定值和主要影響參數的取值范圍；

3)根據AIEM模型各主要影響參數的標定值和不同標準方差產生不同量級的高斯噪聲，對各參數的取值進行隨機擾動，每個量級得到1 000個帶噪聲的采樣值，輸入AIEM模型中得到帶噪聲的后向散射系數集合；

4)通過LUT(look-up tables)方法反演得到Mv，計算反演結果的RMSE和標準方差，研究土壤水分反演RMSE對各影響參數的響應特征，滿足一定反演精度的各影響參數的誤差量級控制范圍；

5)不同入射角時滿足一定反演精度的各影響參數的誤差量級控制范圍。

為了實現敏感性和不確定性的定量分析：

1)對AIEM模型的各輸入參數進行全局敏感性分析，得到各主要參數對模型輸出后向散射系數的影響，確定各參數在模型中的貢獻大小；

2)對臨澤樣區的實測數據的取值范圍進行統計分析，得到AIEM模型輸入參數標定值和主要影響參數的取值范圍；

3)根據AIEM模型各主要影響參數的標定值和不同標準方差產生不同量級的高斯噪聲，對各參數的取值進行隨機擾動，每個量級得到1000個帶噪聲的采樣值，輸入AIEM模型中得到帶噪聲的后向散射系數集合；

4)通過LUT(look-up tables)方法反演得到Mv，計算得到反演結果的RMSE和標準方差，研究土壤水分反演RMSE對各影響參數的響應特征，得到滿足一定反演精度的各影響參數的誤差量級控制范圍；

5)繼續研究不同入射角時滿足一定反演精度的各影響參數的誤差量級控制范圍。

2.1 AIEM模型

AIEM模型是計算隨機粗糙面單次電磁散射問題的近似方法[10]，是目前最廣泛使用的裸露土壤表面散射模型。它從電場和磁場所滿足的積分方程出發，得到了表面上切向電場和磁場的表達式。

AIEM模型單次散射表達式為[11-12]

(1)

(2)

AIEM模型適用于裸土地區的土壤水分反演，而對于農田及低矮植被覆蓋的地區，AIEM模型也適用。Lievens[14]等人在2011年使用水云模型進行了大量試驗，研究發現低矮植被尤其是谷物冠層造成散射衰減在很大程度上可以由直接的冠層貢獻來補償，這導致低矮植被覆蓋區與裸土相比較雷達散射系數相差很小。因此，本研究未考慮作物覆蓋對后向散射系數的影響。

AIEM模型的輸入參數包括傳感器參數和地表參數。其中傳感器參數為入射角θ，地表參數包括Mv，S和l，地表土壤有效溫度st和土壤質地(砂土比例sv和粘土比例cv)。

2.2 AIEM模型參數敏感性分析

由于AIEM模型比較復雜，輸入參數較多，通過對AIEM模型進行參數敏感性分析，得到影響后向散射系數輸出的各參數的貢獻比例，確定主要影響參數，這樣在不確定性分析中就可以對主要影響參數的不確定性進行研究。

本研究中使用擴展傅里葉振幅敏感性分析(Extend Fourier Amplitude Sensitivity Testiing，EFAST)方法來定量分析AIEM模型中各主要輸入參數對后向散射系數的影響[15]。EFAST方法的基本思想來自于貝葉斯定理[16]，即認為模型輸出結果的敏感性可以用模型結果的方差來反映。即參數x的敏感性可以表示為[17]

(3)

式中:Y為模型的輸入值；x為輸入參數；E(Y|X)為當x取某一定值時Y的期望，varx是x遍歷x的取值范圍時的方差。EFAST方法可通過傅里葉變換求得模型中參數i忽略與其他參數耦合以后的一階敏感性指數：

(4)

對于某一參數i在考慮參數耦合作用后的總敏感性指數為

(5)

式中:Si為參數i一階敏感性指數;STi為參數i的總敏感性指數;E(Y|X-i)為E(Y|Xi)的補集。

2.3 有效粗糙度參數的計算

本文使用Rahman的LUT方法來計算有效相關長度。Lievens[14]等試驗了大量不同的(S，l)組合，發現固定住S的取值，通過微波散射物理模型反演得到校準的l，這樣得到的(S，l)組合反演Mv效果較好，并發現S=1 cm，l∈(1 cm,120 cm)時，反演精度較高。

2.4 AIEM模型參數標定

對AIEM模型的主要輸入參數的取值進行統一標定。為盡量貼近試驗實測數據，地表土壤有效溫度取實測平均土壤溫度的均值st=22 ℃；土壤質地參數取值根據“黑河流域HWSD土壤質地數據集”中臨澤地區砂土和粘土比例的平均值來確定，sv=24%，cv=32%；雷達入射角為θ=30°；有效粗糙度參數S=1.4 cm，l=20 cm；土壤水分Mv=30%，見表1。

表1 AIEM模型參數的標定值

2.5 模型參數的不確定性分析

通過敏感性分析，AIEM模型的主要影響參數后，為了定量描述模型主要影響參數的不確定性，根據不同程度的高斯噪聲對各參數值進行隨機擾動，即以表1中標定值為期望，標準差從小到大設置8個不同量級。每個量級生成1 000個加入高斯噪聲的參數集合。將該參數集合輸入AIEM模型得到后向散射系數的模擬集合，然后利用LUT方法反演土壤水分Mv，計算土壤水分的RMSE和方差，并通過響應曲線研究各主要影響因子對反演土壤水分的影響。

2.6 查找表法反演土壤水分

使用基于AIEM模型的LUT[22]法來反演土壤水分，LUT法的核心思想是建立一個簡單高效的查找表(look-up tables，LUT)。首先利用AIEM模型獲取不同粗糙度和土壤水分下的后向散射系數集合，S=1.4 cm，l∈(1 cm,120 cm)，步長為1 cm，Mv∈(1%,60%)，步長為1%，將模擬得到的后向散射數據存儲于表格中為LUT表。

然后利用成本函數在LUT表中查找符合條件的后向散射系數對應的土壤水分值。成本函數為

(6)

3 試驗與分析

3.1 AIEM模型輸入參數敏感性分析

利用開源Matlab工具Simlab軟件的FAST模塊來進行敏感性分析，Simlab是由Joint Research Centre of the European Commission基于蒙特卡洛方法設計的非商業軟件。使用Matlab編程實現AIEM模型主要輸入參數的敏感性分析，在入射頻率給定的情況下(C波段，入射頻率)，AIEM模型的輸入參數包括入射角θ、土壤水分Mv、均方根高度S、相關長度l、地表土壤有效溫度st和土壤質地(砂土比例sv和粘土比例cv)共7個，假設所有參數都為均勻分布。表2為AIEM模型各參數值域范圍，各參數在值域空間內的采樣次數為5 000。

表3顯示了AIEM模型參數的總敏感性指數STi，STi貢獻比例和一階敏感性指數Si。

表3 AIEM模型參數的敏感性指數

由表3可知，AIEM模型各輸入參數中，S，l，Mv和θ這4個參數的貢獻比例相加約96%，一起主導了AIEM模型的后向散射系數輸出。

3.2 參數不確定性量化

根據敏感性分析的結果，選取均方根高度S、相關長度l和雷達入射角θ這3個敏感性參數進行不確定性分析。為了定量描述土壤水分反演過程中S，l和θ這3個參數的不確定性，以表1中的各參數的標定值為期望，不同參數使用不同標準差形成噪聲量級：S(0.01,0.02，0.03,0.04,0.05,0.07,0.09,0.1)，l(0.2,0.4,0.6,0.8,1,2,3,4)，θ(0.2,0.4,0.6,0.8,1,2,3,4)，每個噪聲量級生成1 000個加入高斯噪聲的模型參數集合。圖2為參數S加入量級為0.03高斯噪聲后得到的帶噪聲集合的直方圖。

圖2 帶高斯噪聲(Std=0.03)的S直方圖

從圖2中可以看出，加入不同量級高斯噪聲進行隨機擾動后的參數數值的分布符合正態分布。

將帶不同量級噪聲的參數S集合輸入到AIEM模型中，其他參數使用表1中的標定值，確定帶參數S噪聲的模擬后向散射系數集合，然后利用LUT法反演土壤水分，計算土壤水分反演值的RMSE，圖3為帶不同量級噪聲的S參數對土壤水分反演結果的RMSE響應折線。

使用同樣的方法確定帶不同量級噪聲的l和θ參數對土壤水分反演結果的RMSE響應折線，如圖4和圖5所示。

基于SAR的土壤水分反演一般是在給定入射角范圍的情況下進行，由圖3—圖5可以看出，在雷達入射角為θ=30°情況下，以SMOS土壤水分產品的精度為標準，均方根高度S的誤差量級至少要控制在0.04即標定值的8%以內，才能滿足土壤水分反演精度的要求；同樣，相關長度l的誤差量級至少要控制在0.8即標定值的12%以內；雷達入射角的誤差量級至少要控制在0.6即標定值的6%的范圍內。計算S，l和θ這3個參數不同噪聲量級集合的方差，并計算帶不同量級噪聲的參數集合反演得到的土壤水分的方差，見表4。

圖3 不同噪聲量級S對Mv的RMSE響應折線

圖4 不同噪聲量級l對Mv的RMSE響應折線

圖5 不同噪聲量級θ對Mv的RMSE響應折線

由表4可以看出，隨著各參數噪聲量級和參數集合方差的增大，根據各參數集合反演的土壤水分方差也隨之增大，其中基于帶噪聲的參數S反演的土壤水分的方差變動幅度最為明顯，說明由參數S的不確定性引起的反演土壤水分的不確定最大，而由l和θ的不確定性引起的反演土壤水分的不確定則相對較小。

3.3 不同入射角情形下的參數不確定性

在給定入射角θ=30°情況下的研究，由圖6可以看出，入射角的變化對土壤水分反演精度有較大的影響，為定量描述不同入射角情形下敏感性參數在反演中的不確定性，入射角分別取θ=10°，20°，30°，40°，50°共5個值，以表1中的各參數的標定值為期望，不同參數使用不同標準差形成噪聲量級：S(0.01,0.02，0.03,0.04,0.05,0.07,0.09,0.1)，l(0.2,0.4,0.6,0.8,1,2,3,4)，θ(0.2,0.4,0.6,0.8,1,2,3,4)，每個噪聲量級生成1 000個加入高斯噪聲的模型參數集合。將帶不同量級噪聲的參數S集合輸入到AIEM模型中，利用LUT法反演土壤水分，計算土壤水分反演值的RMSE，圖6為不同入射角情形下帶不同量級噪聲的敏感性參數對土壤水分反演結果的RMSE響應折線。

表4 反演土壤水分不確定性量化統計

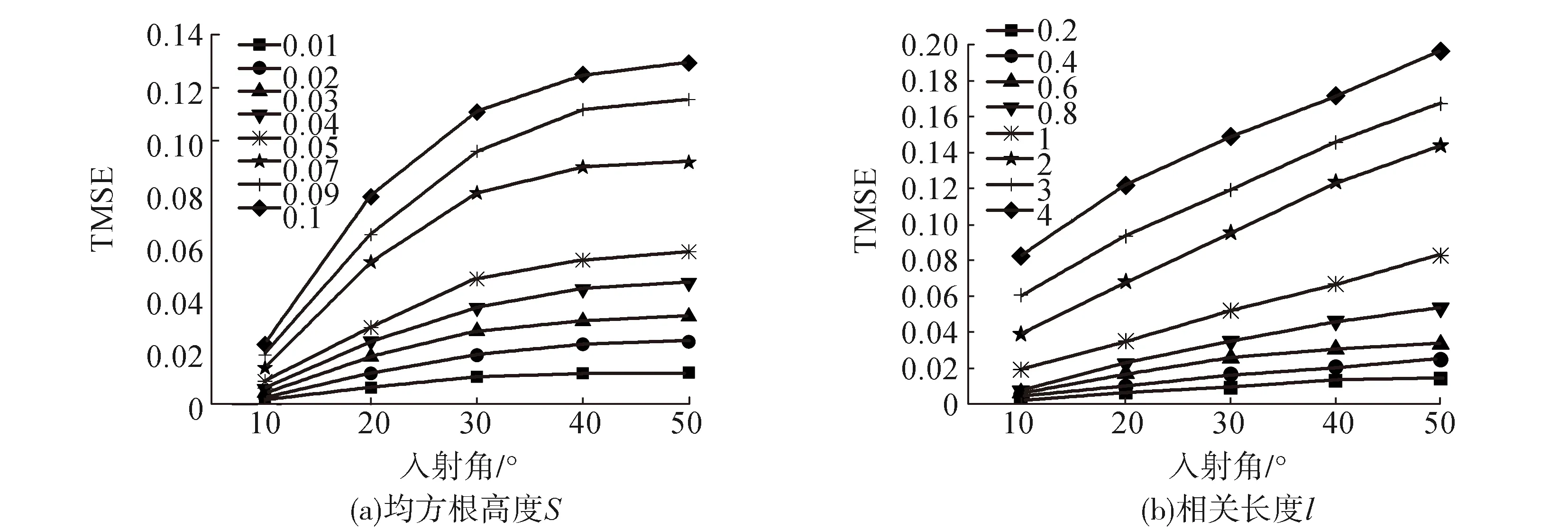
圖6 不同入射角情形下帶不同誤差量級參數時Mv的RMSE響應折線

由圖6可以看出，均方根高度S的噪聲干擾在小入射角時對土壤水分反演結果的影響比大入射角時弱，以SMOS土壤水分產品的精度RMSE=0.04為標準，θ∈(10°,50°)時，S的誤差量級至少要控制在0.03即標定值的2%以內，才能滿足土壤水分反演精度的要求；同樣，相關長度l的噪聲干擾對土壤水分反演也有相似的影響，即在隨入射角的增大，相關長度l的噪聲干擾對土壤水分反演結果的影響也逐漸增大，l的誤差量級至少要控制在0.6即標定值的8%以內。θ∈(10°,50°)時，不同入射角情形均方根高度S和l的誤差量級控制范圍見表5。

表5 不同Q時S和i的誤差量級控制范圍 %

3.4 試驗驗證

為了測試不同入射角情況下敏感參數不確定性對反演結果的影響，本文選取了包含臨澤地區的2008-05-24和2008-07-11一共2幅ASAR數據，入射角θ分別歸一化為20°和30°，利用臨澤樣區中采樣點的土壤水分實測數據，將均方根高度固定為1.4 cm，結合同期ASAR影像中的后向散射數據，利用LUT法反演得到采樣點相應的有效相關長度和土壤水分。使用表5中敏感參數的控制范圍為各敏感參數加入干擾噪聲，然后利用LUT法反演得到帶噪聲的土壤水分，計算各幅ASAR影像中樣區采樣點土壤水分反演值的RMSE，見表6。

表6的結果表明，通過不同入射角情形下的實測數據驗證，本文得到的不同入射角情形均方根高度S和l的誤差量級控制范圍是有效的。

表6 反演土壤水分RMSE

4 結 論

本文通過定量分析AIEM模型各參數的敏感性，選取均方根高度S、相關長度l和雷達入射角θ這3個敏感性參數進行不確定性分析，通過LUT方法研究反演土壤水分過程中的參數不確定性，確定不同入射角情形下S和l的誤差量級控制范圍。使用ENVISAT ASAR影像結合實測土壤水分數據，計算采樣點土壤水分反演值的RMSE，結果表明，本文計算得到的不同θ時S和l的誤差量級控制范圍可有效控制土壤水分反演精度，并適用于較大的入射角范圍。

[1] 李大治,晉銳,車濤,等.聯合機載PLMR微波輻射計和MODIS產品反演黑河中游張掖綠洲土壤水分研究[J].地球科學進展,2014,29(2):295-305.

[2] ENGMAN E T, CHAUHAN N. Status of microwave soil moisture measurements with remote sensing[J]. Remote Sensing of Environment, 1995, 51(1):189-198.

[3] KEYSER E D, VERNIEUWE H, LIEVENS H, et al. Assessment of SAR-retrieved soil moisture uncertainty induced by uncertainty on modeled soil surface roughness[J]. International Journal of Applied Earth Observations & Geoinformation, 2012, 18(1):176-182.

[5] MA C, LI X, NOTARNICOLA C, et al. Uncertainty Quantification of Soil Moisture Estimations Based on a Bayesian Probabilistic Inversion[J]. IEEE Transactions on Geoscience & Remote Sensing, PP(99):1-14.

[6] 李大治.L波段土壤水分反演的不確定性分析及其反演策略研究——以HiWATER PLMR數據為例[D].北京：中國科學院寒區旱區環境與工程研究所,2014.

[7] VERHOEST N E C, LIEVENS H, WAGNER W, et al. On the Soil Roughness Parameterization Problem in Soil Moisture Retrieval of Bare Surfaces from Synthetic Aperture Radar[J]. Sensors, 2008, 8(7):4213.

[8] RAHMAN M M, MORAN M S, THOMA D P, et al. A derivation of roughness correlation length for parameterizing radar backscatter models[J]. International Journal of Remote Sensing, 2007, 28(18):3995-4012.

[9] DAVIDSON M, TOAN T L, MATTIA F, et al. On the characterization of agricultural soil roughness for radar remote sensing studies[J]. IEEE Transactions on Geoscience & Remote Sensing, 2000, 38(2):630-640.

[10] 郭立新，王蕊，吳振森.隨機粗糙面散射的基本理論與方法[M].北京：科學出版社，2010.32-39.

[11] SHI J, CHEN K S, LI Q, et al. A parameterized surface reflectivity model and estimation of bare-surface soil moisture with L-band radiometer[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 40(12):2674-2686.

[12] 余凡, 李海濤, 張承明,等. 利用雙極化微波遙感數據反演土壤水分的新方法[J]. 武漢大學學報(信息科學版), 2014, 39(2):225-228.

[13] 陳晶，賈毅，余凡．雙極化雷達反演裸露地表土壤水分[J]．農業工程學報，2013，29(10)：109-116.

[14] LIEVENS H, VERHOSET N E C, KEYSER E D, et al. Effective roughness modelling as a tool for soil moisture retrieval from C- and L-band SAR[J]. Hydrology & Earth System Sciences Discussions, 2010, 7(4):151-162.

[15] SALTELLI A, TARANTOLA S, CHAN K P S, et al. A quantitative model-independent method for global sensitivity analysis of model output[J]. Technometrics,1999, 41(1): 39-56.

[16] CUKIER R, FORTUIN C, SHULER K,et al.Study of the sensitivity of the coupled reaction systems to uncertainties in rate coefficients: I. Theory[J]. The Journal of Chemical Physics,1973, 59:3873

[17] 郝崇清, 王江, 鄧斌, 等. 基于稀疏貝葉斯學習的復雜網絡拓撲估計[J]. 物理學報, 2012, 61 (14):497-505.

[18] OH Y, HONG J Y. Effect of Surface Profile Length on the Backscattering Coefficients of Bare Surfaces[J]. IEEE Transactions on Geoscience & Remote Sensing, 2007, 45(3):632-638.

[19] SU Z, TROCH P A, DE TROCH F P. Remote sensing of soil moisture using EMAC/ESAR data[C]// Geoscience and Remote Sensing Symposium, 1996. IGARSS ’96.‘Remote Sensing for a Sustainable Future.’, International. IEEE, 1997:1303-1305 vol.2.

[20] BAGHDADI N, HOLAH N, ZRIBI M. Soil moisture estimation using multi‐incidence and multi‐polarization ASAR data[J]. International Journal of Remote Sensing, 2006, 27(10):1907-1920.

[21] ALVAREZ-MOZOS J, CASALI J, GONZALEZ-AUDICANA M, et al. Assessment of the operational applicability of RADARSAT-1 data for surface soil moisture estimation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2006, 44(4):913-924.

[22] 甄珮珮. 基于粗糙度參數的風沙灘地區土壤水分微波遙感反演模型研究[D]. 西安：長安大學, 2016.