基于“稚化思維”理念下的數學“微專題”設計
——以“多元最值問題”為例

☉浙江省象山縣第二中學 呂增鋒

“微專題”是指一個相關聯的、可以單獨研究的知識體系、某種數學思想方法、一個研究主題等.利用“微專題”進行教學具有“因微而準、因微而細、因微而深”等特點，能起到“見微知著”，促進學生深度學習的目的.“微專題”要針對學生存在的“實問題”、“真問題”進行設計，但在實際教學中，教師往往很難準確把握學生的學情，因此，微專題與學生的實際需求存在著“脫節”的現象.那么如何解決這個問題呢？筆者認為應該立足“稚化思維”進行微專題的設計.所謂稚化思維，就是教師把自己的外在權威隱蔽起來，在教學時不以一個知識豐富的教師自居，而是把自己的思維降格到學生的思維水平上，親近學生，接近學生，有意識地退回到與學生相仿的思維狀態，設身處地地揣摩學生的學習水平、狀態等，有意識地發生一種陌生感、新鮮感，以與學生同樣的認知興趣、同樣的學習情緒、同樣的思維情境、共同的探究行為來完成教學的和諧共創.簡而言之，“稚化思維”就是“惑學生所惑、錯學生所錯、難學生所難”.那么具體應該如何操作呢？下面筆者就結合“多元最值問題”微專題的設計，談談對此的做法.

一、以學生的實際需求為起點確定主題

學習過程是一個識知生成的過程，“學”蘊涵著“知”的發生與發展，明確“知什么”有助促進“學”的發生.學生是教學的主體，是課堂上直接的對話者.從表面上看，教師是“教育者”，學生是“被教育者”，但事實上，教學中的思維、決策和行為都是立足于學生的需求而展開的.毋庸置疑，學生才是教師學習與成長中真正的教育者.因此，將微專題的主題定位于“回應學習者需求”才能使微專題發揮應有的功效.微專題的選題一般可以圍繞考點細化、知識點延伸、易錯點辨析、難點突破、思維角度轉化等視角進行，如圖1所示，但具體采用哪個視角，就需要明確學生的實際需求.

圖1

多元最值問題是高中數學學習的重點、難點，也是高考考查的熱點.多元最值問題中以二元問題最為常見，也相對簡單；對于超過二元的問題，要善于將其轉化成二元問題或一元問題.在設計本微專題之前，筆者先對學生存在的問題進行了調查，結果統計如下：根據統計結果，本專題設計的原則是“立足難點易錯點，展現數學思想方法”.基于上述分析，筆者設計了以下微專題.

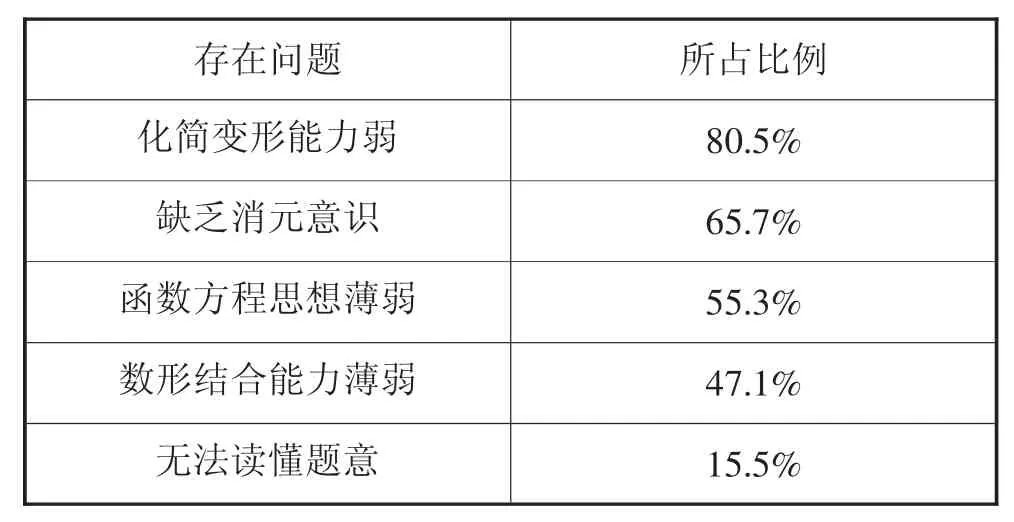
存在問題 所占比例化簡變形能力弱 80.5%缺乏消元意識 65.7%函數方程思想薄弱 55.3%數形結合能力薄弱 47.1%無法讀懂題意 15.5%

例2 x，y，z∈R*，x-2y+3z=0，的最小值為______

練習 1：設x，y為實數，若4x2+y2+xy=1，則2x+y的最大值是______.

意圖：體會基本不等式在解決此類問題中的重要作用，掌握基本的變形方法與激情.

例3 已知任意非零實數x，y滿足3x2+4xy≤λ（x2+y2）恒成立，則實數λ的最小值為______.

例4 設實數a，b，c滿足a2+b2≤c≤1，則a+b+c的最小值為______.

意圖：消元是化歸與轉化的方法.針對多元最值問題，可以先消元轉化為一元問題，再利用函數知識求解.

意圖：數形結合是高中數學又一基本思想，看似一些復雜的代數問題，通過構造幾何模型，以形助數，有柳暗花明又一村的效果.

二、以學生的認知結構為起點分析問題

分析問題要以學生已有的認知結構為基礎，促進學生從原有知識和經驗中構建知識的生長點，通過構建認知“腳手架”，實現從從舊知識到新知識層次的自然過渡.因此，教學設計時教師要盡量避免從數學教材或假想的問題和經驗出發，而是要立足學生真實的問題和經驗.所謂真實的問題就是學生頭腦中真正存在的問題，它是新知識的固著點.因此，把握學生固有認識與新現象、新事實的矛盾是分析問題的關鍵，通過引導學生主動發現這一矛盾，從而引發有效的數學學習活動，實現讓學生學有所思、學有所“成”.

對于例1我們可以多角度進行問題分析.

視角1：二元函數的最值問題，通常有兩個途徑，一是通過消元，轉化為一元函數，再用單調性或基本不等式求解，二是直接用基本不等式，因已知條件中既有和的形式，又有積的形式，不能一步到位求出最值，考慮用基本不等式放縮后，再通過不等式的途徑進行.

方法1：因為4≥2x+2y，x＞y＞0，所以

視角2：元函數的最值轉化為一元函數的最值，從而利用導數研究函數最值，但在處理過程中充分考慮變量的取值范圍，否則容易出錯.

方法3：因為2≥x+y，x＞y＞0，

三、以學生的思維方式為起點提煉方法

學生的思維方式是教學設計的重要依據.教師能否準確把握學生的思維心理和思維特點，能否對學生接受知識的心理作出切合實際的判斷，是教師提煉解題方法的關鍵.為了使教師的思維契合或順應學生的思維，讓兩種思維“合拍”，教師需要設身處地地從學生實際的思維方式出發來進行方法提煉，當教師的思維帶上了學生的色彩，甚至達到了“學生化”之后，方法提煉的過程就自然與學的過程融為一體，為專題設計就會進入一種自然流暢的狀態.

對于“多元最值問題”的解題方法的提煉，可以從“宏觀方法”與“微觀操作”兩大視角進行提煉，具體如圖2所示.

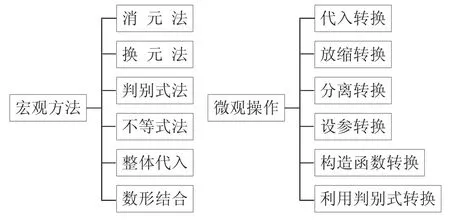
圖2

那么，那種視角更加符合學生的思維呢？“宏觀方法”視角所提煉的方法并不是相互獨立的，而是有“重疊”的，比如，在利用“不等式法”時經常要用到“消元法”、“換元法”、“整體代入法”等，因此，這樣的提煉方式缺乏針對性，容易使學生混淆.“微觀操作”視角就比較符合學生思維，方法的目的性明確，就是為“轉換”，通過“代入”、“放縮”、“設參”等手段把不熟悉的問題轉化為易于學生理解的問題.

微專題在知識的整合和優化上有得天獨厚的優勢，題在教學過程中有效地避免了題海訓練，注重了數學思想的學習感悟，彌補了傳統教學的不足，發揮了學生主體作用.微專題設計的核心是理解學生，而基于“稚化思維”的微專題設計的實質是教師把思維的觸角深入到學生思維的領地，進行發掘、研究和探索，然后跳出學生的思維框架，通過有選擇的模擬，想學生之所想，從而使微專題更加貼近學生實際.H