深入數列本質 構造函數解題

☉河北省秦皇島市山海關第一中學 閻國培

數列本質上是以正整數集為定義域的特殊函數，具有函數的一些特殊性質.對于其中的一些特殊的數列不等式問題，僅從數列的思想方法層面來研究會存在一定的困難，此時從函數層面來思考問題則顯得較為簡單.

一、真題解析，解法點評

1.真題呈現

（2017年浙江卷第22題）已知數列｛xn｝滿足：x1=1，xn=xn+1+ln（1+xn+1）（n∈N*）.證明：當n∈N*時，

（1）0＜xn+1＜xn；

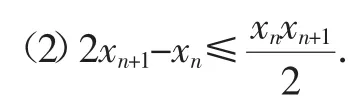
2.試題解析

證明：（1）略.

（2）由xn=xn+1+ln（1+xn+1）＞xn+1，可得xnxn+1=+xn+1·ln（1+xn+1），則xnxn+1-4xn+1+2xn=-2xn+1+（xn+1+2）ln（1+xn+1）.根據上式構造函數，記（fx）=x2-2x+（x+2）ln（1+x）（x≥0），2，函數（fx）在區間［0，+∞）上單調遞增，則在x=0處取得最小值，即（fx）≥（f0）=0.

3.解法點評

上述問題為涉及不等式證明的數列問題，主要考查學生知識的綜合運用以及邏輯思維能力.求解過程由結論出發進行不等式的靈活變形，通過對數列形式的有效分析構造了研究數列不等式的函數，最后利用函數的性質來實現不等式的證明.上述解法是對函數思想解題應用的充分體現，對于涉及數列的單調性和不等式問題.如果能通過形式轉化的方式構造函數，將問題轉化為函數單調性問題來求解，往往會有著良好的解題效果，對于該思路可以進行推廣學習.

二、考題銜接，函數分析

上述利用函數研究數列不等問題是一種較為有效的方法，充分體現了函數與數列的本質聯系性，一般的求解過程是基于理解和分析數列的通項或數列間關系式，通過變形的方式構造與之形式相似的函數，利用函數性質來研究數列問題，其中以單調性最為常用.

試題1 （2015年廣東卷第21題）數列｛an｝滿足a1+

（1），（2）略；

分析：從結論“Sn＜2+2lnn”入手，對其縮放轉化為求不等式左邊含有（n-1）項，可考慮將lnn分解為（n-1）項，因而可將問題轉化為證明，可通過構造函數的方式，利用函數的性質來求解.

（1）求數列｛an｝的通項an；

（2）設Sn=a1+a2+…+an，Tn=a1·a2·…·an，求證

解：（1）略.

在上述數列不等式問題證明過程中都采用了構造函數的方式，利用函數的單調性來證明不等式成立，函數思想是分析數列性質的重要的思想方法.求解的關鍵在于根據題設構造相應的函數，實現原問題的有效轉化.

三、解后反思，教學思考

1.夯實基礎，注重融合

分析近年高考數列問題，高考對數列考查偏向于與其他知識結合，例如不等式、函數等，更加注重考查學生的創新意識與綜合分析能力.但基礎知識仍然是解題的關鍵，試題千變萬化，但仍然是以基礎知識、基本思想作為解題的突破口.教學中也應該相對應地重視學生基礎能力、基本經驗的培養，緊密圍繞教材，緊扣考綱要求，夯實基礎知識，在此基礎上引導學生進行知識的有效融合，鍛煉學生思維的的靈活性，特別要加強知識融合后解題方法的學習，以提高學生解題能力為教學出發點.

2.思想學習，發展思維

數列是一種以正整數集為定義域的特殊函數，所以對于特定問題可以從函數性質角度來研究，可通過構造函數的方式，利用函數模型來研究數列問題，從而拓寬解題的思路.數列的構造思想和模型化思想是高考的難點，課改的推進促進了題型的綜合演變，但沒有降低對數學思想的考查要求，反而相應的有所上升.利用構造思想，將數列問題轉化為函數問題是研究數列問題的一種重要思路，在教學中要以培養學生的推理能力和構造思想為教學重點，力求在思想上提高學生的數學能力，發展學生的數學思維.

3.注重創新，提升能力

創新是高考永恒不變的主旋律.近年的高考數列試題也越發注重對學生創新意識的考查，以數列問題為例，問題考查遵從層次型、遞進型、思維情景型，使學生便于理解、探究、創造、深入反思問題，充分理解數列知識的核心重點，從而掌握相關的數學思想.在教學中也應該注重知識的創新學習，充分利用教學資源，重現數列發展演變規律，培養學生的創新意識，激活創新思維，使學生可以很好地應對高考創新題，并提升自身的整體創新能力.

四、總結提高

數列不等式問題的解決要從數列的本質出發，充分結合數列的函數特性，利用函數單調性來解析數列規律，從而促進問題的高效解決.在教學中要引導學生研究和討論數列與函數的聯系，注重基礎知識的學習，掌握解題的思想方法，培養創新意識，從思想上提升解題能力.

1.朱松.證明數列不等式的幾點做法［J］.中學數學（上），2017（3）.

2.張定強，閆佳潔.2016年全國高考試卷中“數列”試題分析［J］.中學數學（上），2016（11）.

3.章建斌.探究問題本真，突破教學壁壘——由一道高考壓軸題引發的教學反思［J］.數學教學通訊，2017（15）.

4.童昌盛.一道數列不等式證明方法的深入探究［J］.數學教學通訊，2017（15）.H