基于Donnell-Mushtari理論的彈性基礎薄壁圓柱殼的穩態響應研究

楊永寶， 危銀濤， 李雪冰， 張新月

(1.清華大學 汽車安全與節能國家重點實驗室，北京 100084； 2. 燕山大學 車輛與能源學院，秦皇島 066004)

薄壁圓柱殼作為一種簡單、高效的結構在各工程領域均得到廣泛應用，如常見的輪胎、油罐、飛機、潛艇等具體部件。但類似結構在受到外界復雜激勵作用后易出現失穩等現象而影響正常工作，故薄壁圓柱殼動力學特性的研究對此類結構的設計和分析有重要工程意義。

有關文獻十分豐富，尤其是針對簡支、固支等經典邊界條件下圓柱殼固有振動特性的研究[1-8]。Leissa[9]在著名的殼振動理論一書中對數量眾多的文獻進行了綜述，系統總結了常見殼理論及不同類型殼的自由振動問題。許多學者基于不同殼理論對經典邊界條件下圓柱殼的振動響應進行了針對性研究。Sheng等[10-11]分別基于Donnell理論與Novozhilov殼體理論對簡支條件下的各向同性圓柱殼響應問題進行研究。Christoforou等[12]針對簡支條件下的正交各向異性圓柱殼受到徑向沖擊后的響應問題展開研究。Jafari等[13]基于love殼理論對復合材料圓柱殼的自由和強迫振動響應展開研究，邊界條件為固支-自由邊界。馬旭等[14]在波傳播分析方法基礎上，采用改進傅里葉級數的方法給出了兩端彈性基礎上的圓柱殼在任意徑向點力激勵下的振動響應，實質是用梁彎曲振動模態振型來近似柱殼軸向振型以實現圓柱殼振動在周向與軸向的解耦，在某些情況下誤差較大。還有許多類似研究[15-18]，但主要是簡支等經典邊界條件下圓柱殼的穩態響應研究，而針對兩端彈性邊界條件下薄壁圓柱殼(以下簡稱彈性基礎圓柱殼)穩態響應的求解研究尚比較欠缺，有關研究還存在誤差較大等問題。

本文針對彈性基礎上有徑向預壓力作用的圓柱殼展開研究。基于經典的Donnell-Mushtari柱殼理論，對圓柱殼的固有振動特性進行分析，求得諧波激勵作用下的強迫振動穩態響應，并針對所取基礎模態數量及阻尼系數大小對于薄壁圓柱殼穩態響應的影響進行了討論研究。

1 固有振動特性

薄壁圓柱殼模型如圖1所示，建立柱坐標系(x,θ,r)，x,θ,r分別為其軸向、周向和徑向的坐標軸，u,v,w分別為柱殼中面上任一點的軸向、周向和徑向位移，圓柱殼的長度為L，平均半徑為R，厚度為h。在圓柱殼的兩端均布相應的軸向、周向、徑向和扭轉方向的彈簧，剛度分別為ku,kv,kw,kφ。

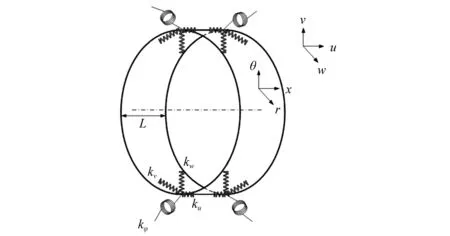
圖1 圓柱殼及相應的坐標系示意圖Fig.1 Cylindrical shell and coordinate systems

柱殼自由振動控制方程為

(1)

式中：L(u,v,w)為相應的微分算子。

基于經典的Donnell-Mushtari柱殼理論，考慮在圓柱殼內壁上沿徑向均勻分布的初始內壓力P0，得到自由振動微分方程為

(2)

(3)

(4)

其中，

(5)

假設圓柱殼的位移表達式為

(6)

將上述位移表達式(6)代入振動微分方程式(2)～式(4)中，可得表達式

(7)

若式(7)有非零解，則左側矩陣行列式結果為零。整理可得到關于λ的8次特征方程為

λ8+g3λ6+g2λ4+g1λ2+g0=0

(8)

其中，

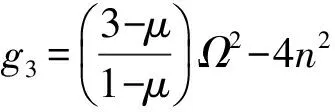
(9)

(10)

式中：n為周向波數；ω為圓頻率；Ω為無量綱頻率參數。

特征方程式(8)是一個與軸向波數有關的無量綱參數λ的8次方程，有正負兩組共8個解λi(i=1, 2, …, 8)，解的可能形式有實數、虛數和復數三種，λi為純實數時代表軸向的傳播波，λi為純虛數時為軸向的近場波，λi為復數時代表沿軸向衰減的傳播波[19]。特征方程式(8)，隨著參數的變化，會出現不同類型的根值，理論上共有九種不同組合形式的根值，而不應簡單的直接假設為某些特定類型，如一對純實根、一對純虛根和兩對復根，否則可能會出現漏解問題。本文充分考慮了這一點，避免了類似問題產生，同時得到精確解。

基于特征方程式(8)得到根值表達式，代入方程式(7)，求得振幅比系數ηi和εi

(11)

進而將3個方向的位移表達式寫出

(12)

對不同的邊界條件，薄壁圓柱殼的位移和內力等將對應滿足不同的條件。

對兩端彈簧支撐邊界條件下的薄壁圓柱殼，當x=-L/2時，滿足

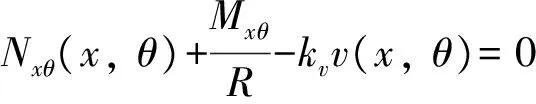
(13)

當x=L/2時，滿足

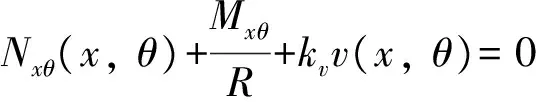
(14)

式(13)和式(14)中，

(15)

將式(12)代入式(13)和式(14)中，整理之后得到關于C1～C8的八元齊次代數方程組，若方程組存在相應的非零解，則系數行列式結果為0，可求得薄壁圓柱殼的固有頻率及對應的模態振型。

求解過程沒有進行做任何近似，因此計算所得結果是基于Donnell-Mushtari理論所得到的最精確計算結果。

2 穩態響應

為簡化相應表達式和計算過程，求解穩態響應時，不考慮圓柱殼內部壓力的影響。

在外載荷激勵作用下，薄壁圓柱殼滿足下列動力學方程

(16)

上述動力學方程的解可設為

(17)

將以上解代入外載荷作用下的動力學方程中，可得

(18)

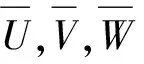
(19)

因此，整理式(18)、式(19)后可得到

(20)

(21)

其中，對應廣義力Fmn(t)為

(22)

對應的廣義質量Mmn為

(23)

利用二階微分方程式(21)，求解得到每階模態所對應的Tmn(t)值，然后將結果代入式(17)，即可求得相應的強迫振動穩態響應結果。

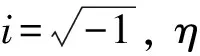
若作用在u、v方向的激勵力為0，w方向的激勵力fw為

fw=f0eiωtδ(θ-θ*)δ(x-x*)

(24)

則，對應的廣義力為

(25)

有關Tmn(t)的二階微分方程則變為(m,n指相對應的模態階次)

(26)

將每階模態所對應的廣義力和廣義質量等代入式(26)，求得各階模態所對應的Tmn(t)，并將所得結果代回式(17)中，求得強迫振動響應。

基于式(26)可求得Tmn(t)

(27)

若激勵力為正弦波信號f0sin(ωt)，初始條件為0，則模態坐標通解取式(27)的虛部，為

(28)

(29)

3 算例分析

3.1 與文獻中結果的對比

為驗證本文理論計算方法的準確性，本節針對兩個經典算例，將本文計算方法所得結果與有關文獻中的數據進行對照，如表1和表2所示。其中，Karczub中的計算結果基于Flügge經典薄殼理論得到，文獻[20]采用的是有限元分析方法，Li采用了波傳播方法。

表2給出了通過本文計算方法得到的固有頻率結果及有關文獻中的數據，對比結果顯示，本文方法的計算誤差較小，結果準確。

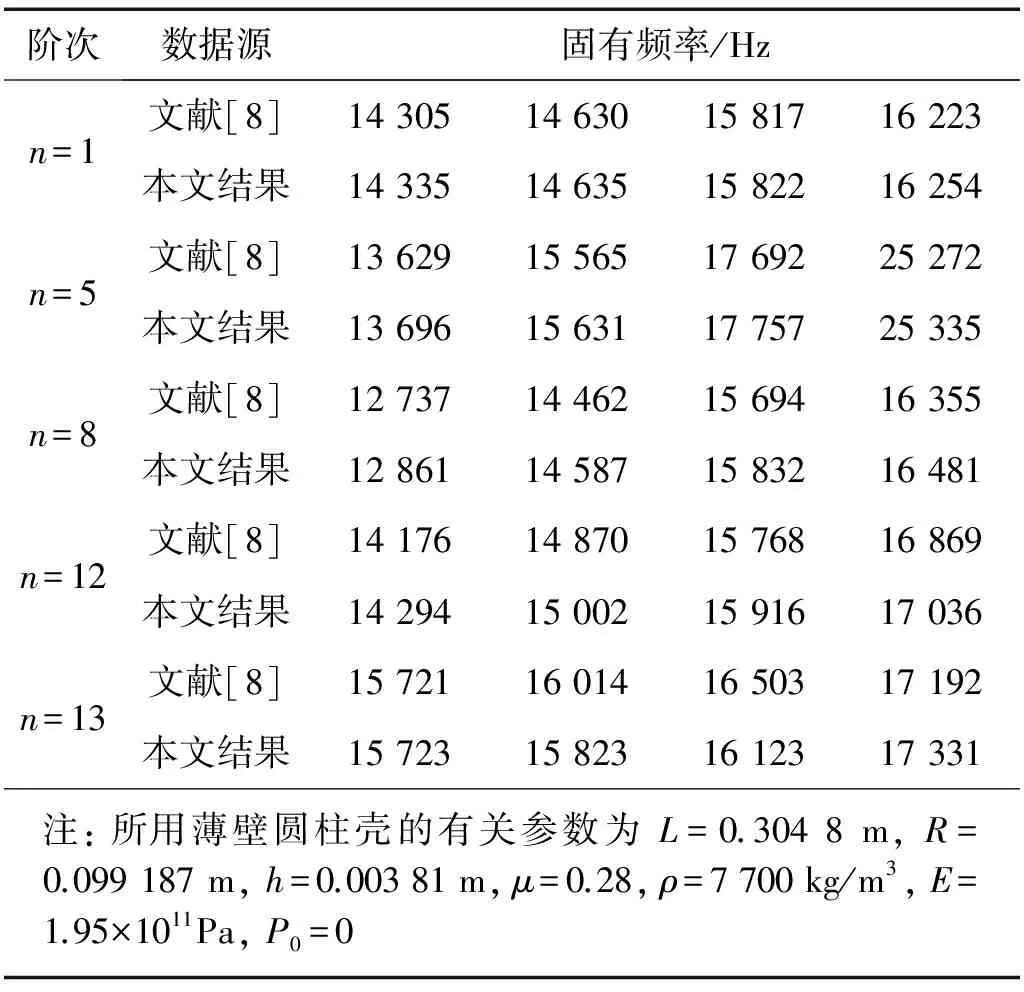
表1 簡支但有軸向位移約束的邊界條件下， 基于本方法所得結果與有關文獻所得結果的對比

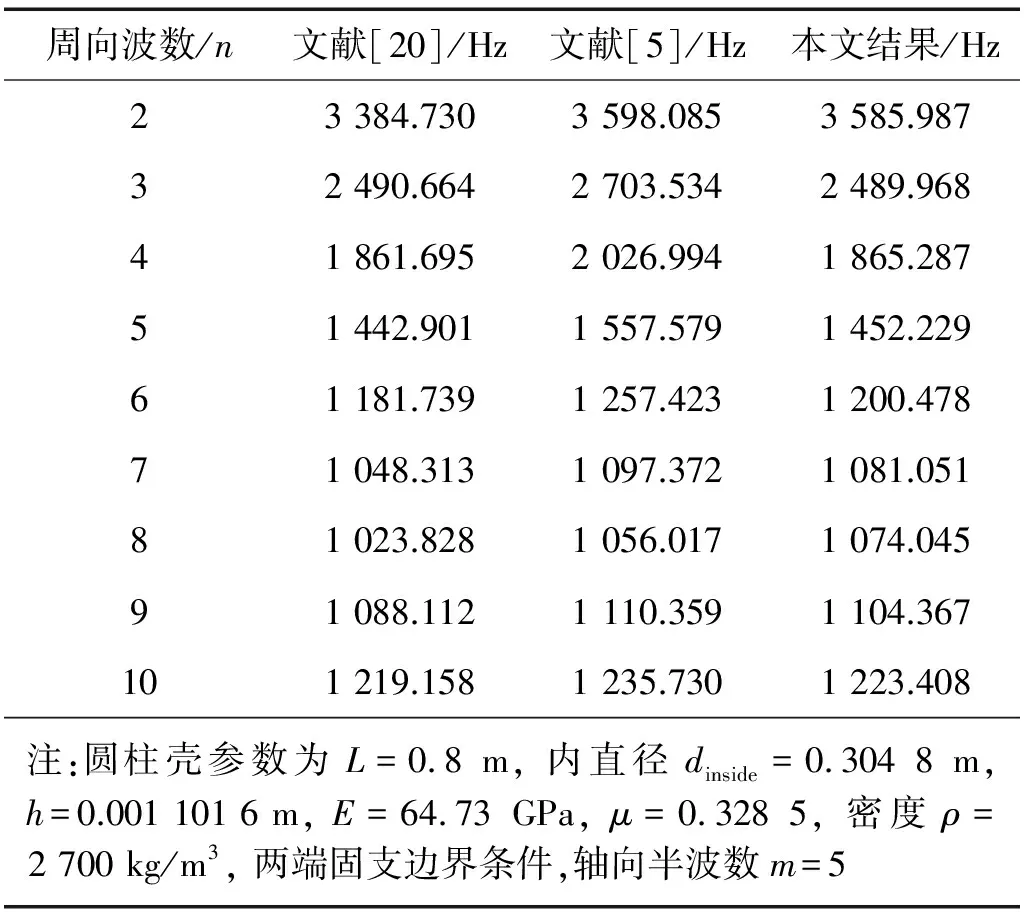
表2 固有頻率的理論計算結果與文獻中結果對照

3.2 參數分析

為分析不同周向波數和軸向半波數與圓柱殼固有頻率的關系，分別采用有限元方法和本文方法進行算例分析，模型參數為：R=0.5 m,h=0.01 m,L=4 m,E=1.5×1011Pa,μ=0.3,ρ=7 000 kg/m3，圓柱殼兩端的徑向均布彈簧的剛度kw=1 000 N/m, 內壓力P0=0。 其余彈簧剛度為0，得到結果如圖2所示。

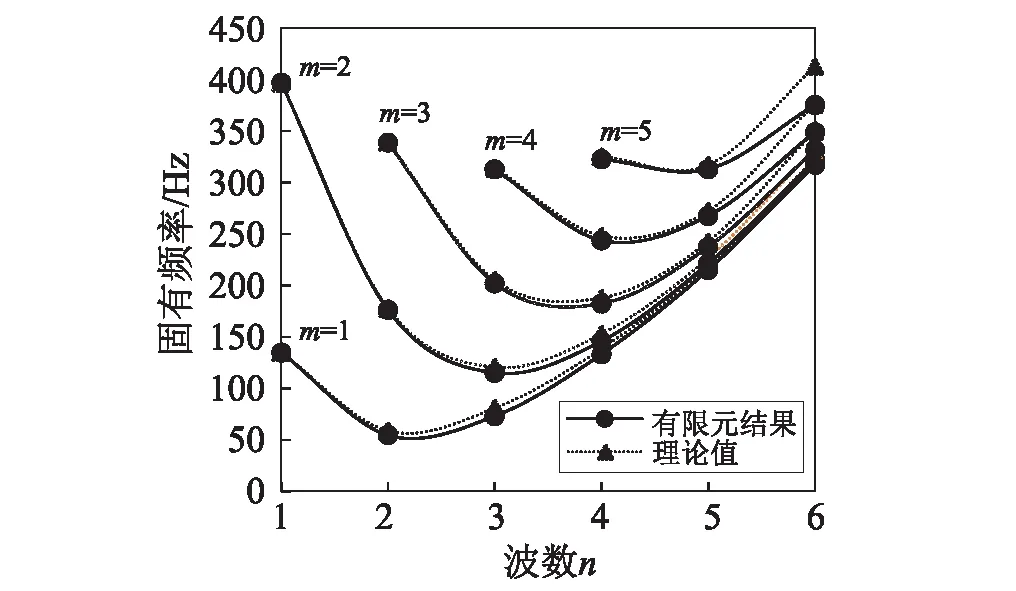
圖2 波數與薄壁圓柱殼固有頻率間的關系Fig.2 Correlation between wave number and free vibration frequency of thin-walled cylindrical shell

從圖2可得以下幾點結論：本文計算得到的薄壁圓柱殼固有頻率與有限元方法計算得到的結果比較一致；隨著軸向半波數的增加，圓柱殼的固有頻率總體呈增大趨勢；而在不同的軸向半波數下，周向波數與固有頻率間的關系總體上也是一致的，隨n值的增加先降低而后升高，且變化趨勢隨軸向半波數的變化而略有不同。

4 穩態響應的計算和討論

基于本文方法可對任意邊界條件的下的薄壁圓柱殼進行自由振動頻率和穩態響應的計算，本文以徑向簡單支撐彈簧邊界條件為例進行計算和討論。有關參數同4.2節的算例。

4.1 諧波激勵下的柱殼穩態響應

設外力作用在薄壁圓柱殼的(L/2,0)位置處，激勵為fsin(ωt),f=1 N。

利用本文方法，首先基于圓柱殼的有關參數計算得到前25階固有頻率及對應模態振型，之后基于模態數據進行疊加計算，得到穩態響應幅頻曲線，如圖3所示。

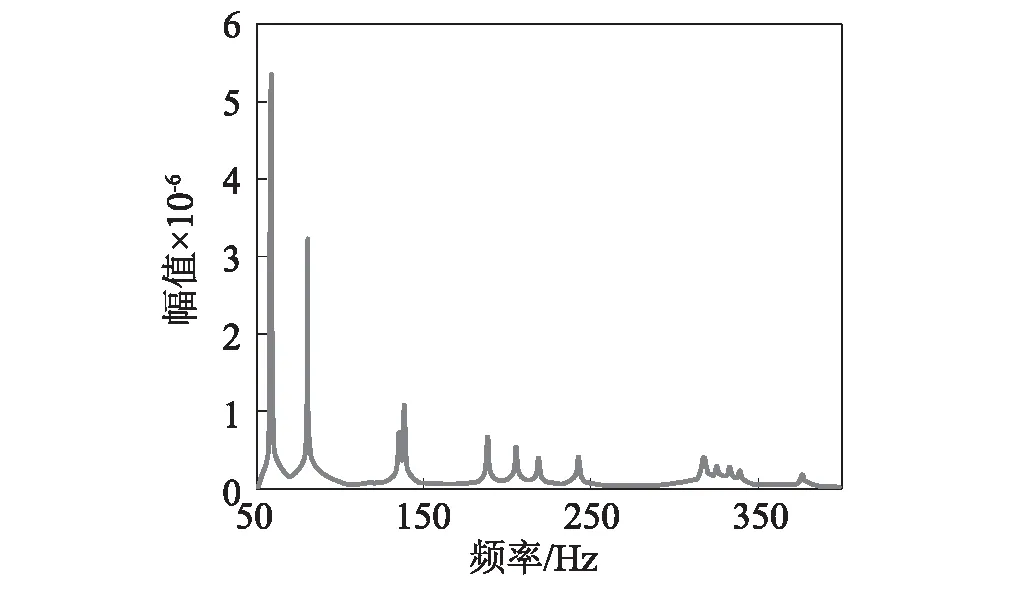
圖3 圓柱殼穩態響應幅頻曲線Fig.3 Amplitude-frequency response curve of cylindrical shell

從圖3可看出，在最低階次模態所對應的58.76 Hz頻率處，出現了最大的徑向位移響應。而后，隨著頻率的增加，徑向位移響應總體上呈降低趨勢。某些階次模態所對應的徑向位移較小，因此未在幅頻曲線中顯著體現。

4.2 所用模態數量的影響

計算圓薄壁圓柱殼的穩態響應時，模態截斷數量對于穩態響應的計算會產生影響。為分析這種影響，分別使用前6階、12階及25階模態來計算薄壁圓柱殼在諧波激勵下的徑向位移穩態響應，得到如圖4～圖6所示結果。

觀察圖4～圖6圓柱殼穩態徑向位移響圖不難發現，對于前幾階振動模態，選擇使用前6階模態、12階模態及25階基礎模態疊加計算所得徑向響應位移值的變化幅度很小。即對于兩端彈簧支撐條件下受到徑向諧波激勵時的薄壁圓柱殼的穩態位移響應求解問題，采用數量較少的基礎模態也可滿足基本精度要求。對本文算例，只需要前6階基礎模態數據即可實現很小的計算誤差，以圖6結果為基準，計算得到的第一階模態所對應的徑向位移誤差僅為0.37%。

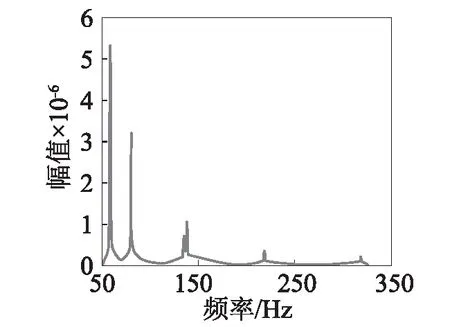
圖4 基于前6階模態疊加計算得到的穩態響應幅頻曲線Fig.4 Amplitude-frequency curve of steady-state response based on the superposition of first six modes

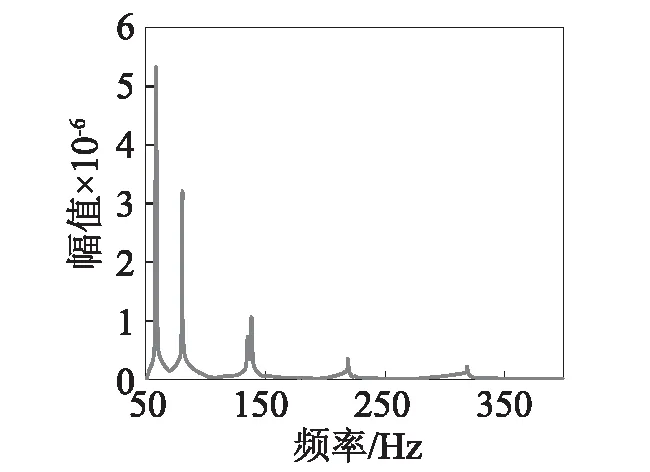
圖5 基于前12階模態疊加計算得到的穩態響應幅頻曲線Fig.5 Amplitude-frequency curve of steady-state response based on the superposition of first twelve modes

圖6 基于前25階模態疊加計算得到的穩態響應幅頻曲線Fig.6 Amplitude-frequency curve of steady-state response based on the superposition of first twenty-five modes

4.3 阻尼系數的影響

在計算圓柱殼的位移穩態響應時，須計入阻尼的影響，為分析阻尼系數對于圓柱殼位移穩態響應的影響，基于計算得到的前25階模態數據，分別求解阻尼因子為0.005、0.010、0.015條件下的圓柱殼的徑向位移響應，得到如圖7所示的幅頻特性曲線。

從圖7不難看出，阻尼對薄壁圓柱殼的穩態位移響應影響顯著，隨著阻尼因子的增加，圓柱殼的徑向位移響應出現顯著的減小。在較高頻段，幅頻曲線變得平滑，沒有了明顯峰值。

圖7 三種不同阻尼因子條件下的薄壁圓柱殼徑向位移幅頻響應Fig.7 Amplitude-frequency curve of radial displacements of thin-walled cylindrical shell for three different damping factors

6 結 論

本文基于經典的Donnell-Mushtari圓柱殼振動理論，得到了考慮初始內壓力的彈性基礎上薄壁圓柱殼的固有頻率及強迫振動穩態響應的計算公式。主要結論可歸納如下：

(1)本文方法計算所得結果與有關文獻中的數據結果相比較，誤差較小，精度較高。

(2)基于本文算例，較少數量的模態疊加即可實現較為精確的穩態響應計算。即選擇適當數量的基礎模態用于薄壁圓柱殼穩態響應疊加計算，可在保證精度的情況下提高計算效率。

(3)基于本文算例，阻尼因子對于薄壁圓柱殼穩態響應的影響較大，當阻尼因子增大時，柱殼的穩態響應將顯著減小，穩態響應幅頻曲線的部分峰值變得不明顯。

(4)本文方法不僅可針對一般的彈性基礎邊界條件下的薄壁圓柱殼的自由振動及諧波激勵穩態響應進行求解，還可用于解決其他各種邊界條件下的薄壁圓柱殼的振動特性問題。

[ 1 ] SAITO T, ENDO M. Vibration of finite length, rotating cylindrical shells[J]. Journal of Sound and Vibration, 1986, 107(1): 17-28.

[ 2 ] SMITH B L, VRONAY D F. Free vibration of circular cylindrical shells of finite length[J]. AIAA Journal, 1970, 8(3): 601-603.

[ 3 ] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration, 2001, 239(3): 397-403.

[ 4 ] IP K H, CHAN W K, TSE P C, et al. Vibration analysis of orthotropic thin cylindrical shells with free ends by the rayleigh-ritz method[J]. Journal of Sound and Vibration, 1996, 195(1): 117-135.

[ 5 ] LI Xuebin. Study on free vibration analysis of circular cylindrical shells using wave propagation[J]. Journal of Sound and Vibration, 2008, 311(3): 667-682.

[ 6 ] DYM C L. Some new results for the vibrations ofcircular cylinders[J]. Journal of Sound and Vibration, 1973, 29(2): 189-205.

[ 7 ] SOEDEL W. Simplified equations and solutions for the vibration of orthotropic cylindrical shells[J]. Journal of Sound and Vibration, 1983, 87(4): 555-566.

[ 8 ] KARCZUB D G. Expressions for direct evaluation of wave number in cylindrical shell vibration studies using the Flügge equations of motion [J]. The Journal of the Acoustical Society of America, 2006, 119(6): 3553-3557.

[ 9 ] LEISSA A W. Vibration of shells[M]. New York: Acoustical Society of America, 1993.

[10] SHENG J. The response of a thin cylindrical shell to transient surface loading [J]. AIAA Journal, 1965, 3(4): 701-709.

[11] WARBURTON G B. Harmonic response of cylindrical shells [J]. Journal of Engineering for Industry, 1974, 96(3):

994-999.

[12] CHRISTOFOROU A P, SWANSON S R. Analysis of simply-supported orthotropic cylindrical shells subject to lateral impact loads [J]. Journal of Applied Mechanics, 1990, 57(2): 376-382.

[13] JAFARI A A, KHALILI S M R, AZARAFZA R. Transient dynamic response of composite circular cylindrical shells under radial impulse load and axial compressive loads [J]. Thin-Walled Structures, 2005, 43(11): 1763-1786.

[14] 馬旭, 杜敬濤, 楊鐵軍, 等. 基于波傳播方法的邊界條件對圓柱殼振動特性的影響分析[J]. 振動工程學報, 2009, 22(6): 608-613.

MA Xu, DU Jingtao, YANG Tiejun, et al. Analysis of influence of boundary conditions on cylindrical shell dynamics based on wave propagation approach [J]. Journal of Vibration Engineering, 2009, 22(6): 608-613.

[15] 王宇, 羅忠. 薄壁圓柱殼構件受迫振動的響應特征研究[J]. 振動與沖擊, 2015, 34(7): 103-108.

WANG Yu, LUO Zhong. Forced vibration response characteristics of thin cylindrical shell [J]. Journal of Vibration and Shock, 2015, 34(7): 103-108.

[16] 羅忠, 王宇, 孫寧, 等. 不同邊界條件下旋轉薄壁短圓柱殼的強迫振動響應計算[J]. 機械工程學報, 2015, 51(9): 64-72.

LUO Zhong, WANG Yu, SUN Ning, et al. Forced vibration response calculation of rotating short thin cylindrical shells for various boundary conditions [J]. Journal of Mechanical Engineering, 2015, 51(9): 64-72.

[17] 李學斌. 圓柱殼穩態動力響應分析[J]. 艦船科學技術, 2000 (6): 1-5.

LI Xuebin. Steady-state dynamic response analysis of cylindrical shell[J]. Ship Science and Technology, 200(6): 1-5.

[18] 左言言, 宮鎮. 圓柱殼受激振動的分析研究[J]. 農業機械學報, 1998, 29(1): 88-93.

ZUO Yanyan, GONG Zhen. Study on the excited vibration of a cylindrical shell[J]. Transactions of the Chinese Society for Agricultural Machinery, 1998, 29(1): 88-93.

[19] 陳正翔, 江松青. 圓柱殼中結構振動波的傳播特性[J]. 振動工程學報, 1998, 11(4): 450-456.

CHEN Zhengxiang, JIANG Songqing. Dispersion characteristics of structure vibration waves in cylindrical shells [J]. Journal of Vibration Engineering, 1998, 11(4): 450-456.

[20] SANTIAGO J M, WISNIEWSKI H L. Convergence of finite element frequency prediction for a thin walled cylinder [J]. Computers and Structures, 1989, 32(3/4): 745-759.