含改進LuGre動摩擦的非光滑振動系統的動力學分析

2018-03-28 07:26:04張艷龍唐斌斌

振動與沖擊 2018年6期

張艷龍，王麗，唐斌斌

(1 蘭州交通大學機電工程學院，蘭州 730070；2 蘭州城市學院數學學院，蘭州 730070)

含摩擦及間隙的碰撞振動機械系統普遍存在工程應用中，如制動振動與尖叫、沖擊旋轉鉆井、裝于滑動軸承上的大型高速轉子的油膜振蕩、離合顫振、機器人關節處的摩擦誘導振動、噪聲控制等。摩擦及間隙構成的強非線性系統，吸引了眾多國內外學者致力于建立不同的力學模型和摩擦模型，來研究摩擦及間隙對系統動力學的影響。文獻[1]從一類軸承模型中簡化出含間隙及摩擦的單自由度碰撞振動系統，進行動力學分析發現黏著的存在，并且可以用來預測螺栓的松動；文獻[2]研究單邊約束的兩自由度塑性碰撞振動系統，分析分段特性、擦邊奇異性和參數變化對碰撞振動系統的影響；文獻[3-5]利用含有干摩擦的Filippov振動系統研究滑移分岔和混沌動力學行為；文獻[6-7]利用增量諧波平衡法研究了含分段阻尼和剛度的非線性系統；丁旺才等[8]結合Lyapunov指數數值仿真分析了兩自由度干摩擦振動系統的動力學響應得到系統經周期運動失穩通向混沌的道路；錢大帥等[9]利用諧波平衡法研究了干摩擦質塊雙黏著運動響應的級數形式解及對黏滑邊界的分析。上述文獻建立和研究不同含有靜摩擦及間隙的力學模型，分析和解釋工程中的振動。

實際上，兩接觸物體之間的摩擦，其摩擦力不僅由摩擦接觸表面的相對速度決定，還取決于兩接觸物體之間的某些內部變量和影響因素，如兩接觸物體之間摩擦溫度及粗糙度等，一般將粗糙度簡化為鬃毛剛度(Bristle Stiffness)和鬃毛阻尼(Bristle Damping)等，稱此類摩擦模型為動摩擦模型，如LuGre動摩擦模型[11]、Dankowicz動摩擦、改進的LuGre動摩擦模型。動摩擦模型深入到微觀，從宏觀和微觀兩方面探討摩擦性質，動摩擦模型本身具有動力學特性，能夠更加深入地描述兩物體接觸面之間的摩擦狀態。文獻[12]對含有LuGre動摩擦的兩自由度制動系統進行穩定性分析，研究動摩擦對系統的動力學影響。Saha等[13-14]針對含LuGre動摩擦、改進的LuGre動摩擦和Dankowicz動摩擦的單自由度光滑振動系統，通過多尺度法得出系統發生Hopf分岔的次臨界和超臨界分岔點，比較了不同系統參數變化下的相軌跡；Saha等[15]針對含改進LuGre動摩擦的單自由度光滑系統，通過相圖說明系統存在黏滯運動，選取不同的系統參數分析了帶與質塊的相對速度對摩擦特性曲線影響，說明了改進和未改進LuGre動摩擦對系統行為的影響。本文在文獻[15]的基礎上將改進的LuGre動摩擦模型引入含分段阻尼和剛度的碰撞振動系統，對系統的運動過程進行分類討論，通過數值仿真探討含分段阻尼和剛度及改進的LuGre動摩擦的單自由度非光滑系統存在的摩擦誘導振動現象以及系統運動在滑移-黏滯-碰撞接觸-顫振之間轉換的動力學行為。將改進的LuGre動摩擦模型運用到此類系統模型中可以更全面地描述摩擦誘導振動特性以及對機械機構的參數優化、運動過程控制等起到很好的理論指導意義。

1 力學模型

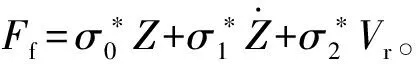
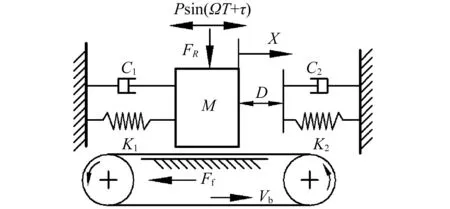
圖1 含改進的LuGre動摩擦的非光滑振動系統力學模型Fig.1 Mechanical model of non-smooth vibration system with modified LuGre dynamic friction

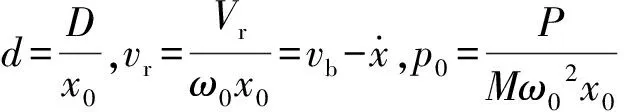
(1)

質塊M在x=d處發生碰撞，構成非光滑振動系統，根據碰撞定律可得

(2)

改進的LuGre動摩擦力的無量綱為

(3)

鬃毛剛度均勻形變z的演化由式(4)支配

(4)

式中：w1>0和w2>0是兩個常量；函數g(vr)為高斯模型

g(vr)=fR(μk+(μs-μk)e-(vr/vs)2)

(5)

系統含分段阻尼和彈簧及改進的LuGre動摩擦構成的非連續運動，質塊的運動狀態將會在滑移、黏滯、顫振與碰撞之間相互轉換，運動過程變的復雜。為了能夠更好的理解系統的運動狀態變化，根據質塊的受力和速度變化情況，將運動過程分情形討論：

情形1質塊與帶相對滑移運動

(6)

情形2質塊與帶相對黏滯運動

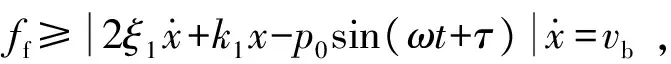
(7)

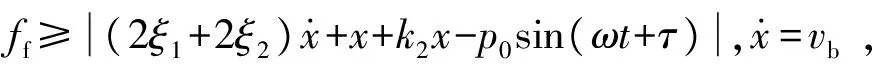
(8)

情形3質塊靜止狀態

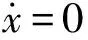
(9)

情形4質塊與擋板碰撞運動

質塊為M的質塊在x=d處與右邊的擋板發生彈性碰撞接觸，根據碰撞關系得

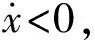
(11)

如果當質塊第i次接觸約束面時，質塊與帶的相對速度為零或在零附近波動，質塊所受合力小于0

(12)

質塊將會在約束面處發生顫振或黏滯，直到質塊所受合力的方向發生改變，質塊重新回到滑移運動狀態。

如果當質塊第i次接觸約束面時，質塊與帶的相對速度為零或在零附近波動，質塊所受合力大于等于0

(13)

質塊M將不會在約束面處發生顫振或黏滯，質塊所受合力會將質塊M從顫振或黏滯狀態拉離約束面。

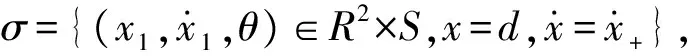
2 振動系統的黏滑顫振動力學分析

2.1 黏滑運動

選取系統參數一：k2=0.5，ξ1=0.5，ξ2=2.5 ，d=0.8，p0=2.5，vb=0.35，vs=0.25，μ=0.3，μk=0.3，μs=0.3，fR=10.5，w1=1，w2=1，σ0=100，σ1=10，σ2=1，對系統進行動力學分析，以激振頻率ω為分岔控制參數，局部分岔圖2(a)呈現出質塊的運動速度與激振頻率ω的分岔關系，速度大于零的部分取質塊與擋板碰撞接觸時的Poincaré截面；為了更清楚的了解系統隨控制參數的變化情況，得到速度小于零的部分取質塊與擋板接觸分離時的Poincaré截面得到的分岔圖如圖2(b)所示，由于分岔圖中得不到系統的黏滯情況，具體的黏滯運動見相圖所示；圖3(a)展示了質塊和帶的相對與改進的LuGre摩擦力之間的關系，動摩擦模型可預測在純滑移區域的順時針和逆時針兩種不同的遲滯環及下垂摩擦特性，摩擦力隨著相對滑移速度的增長的變化關系；圖3(b)呈現出質塊的運動速度與帶速vb之間的變化關系。相圖和Poincaré映射圖如圖4(a)～圖4(d)所示，時間歷程圖如圖4(e)～圖4(h)所示。將含改進的LuGre動摩擦模型引進含有分段剛度阻尼約束的碰撞接觸系統運動中，動摩擦對系統運動的動力學行為轉換有著重要的影響，尤其是系統在滑移運動與黏滯運動之間的轉換。具體詳細運動過程分析如下，質塊在動摩擦力及激振力共同作用下，系統的動力學行為發生著復雜的運動變化。圖4(a)和圖4(e)呈現出系統在激振頻率ω=1.8時發生周期1-1-0運動，質塊在運動過程中與擋板發生一次碰撞接觸和一次接觸分離，在相圖中碰撞接觸點用黑圓點表示，接觸分離點用黑叉點表示，圖4(b)～圖4(d)表示相同，相軌跡表現出質塊無黏滯運動，質塊的運動狀態在滑移與碰撞之間相互轉換；隨著激振頻率的減小，當ω=0.9時系統發生周期1-1-1黏滯運動，由Poincaré映射可以很清楚的看出系統在碰撞面處，發生了一次碰撞接觸和一次黏滯運動，如圖4(b)和圖4(f)所示；當激振頻率降到ω=0.3時系統發生周期1-2-1運動，系統的動力學行為在滑移-接觸碰撞-分離接觸-黏滯之間轉換，具體分析過程以黏滯結束點A作為質塊運動的起點，質塊在A點被迫與擋板碰撞，碰撞接觸后與擋板一起進入滑移運動，質塊到達B點與擋板分離，再次以滑移狀態運動到D點，與擋板發生第二次碰撞接觸，碰撞接觸后與擋板共同滑移到E點，質塊在E點與擋板分離，質塊與擋板分離后，質塊滑移運動到F點，開始進入黏滯狀態，與帶黏滯運動到A點，質塊的一個周期運動結束，質塊在滑移-碰撞接觸-黏滯之間的運動過程轉換如相圖4(c)和時間歷程圖4(g)所示；圖4(d)和圖4(h)呈現出的系統發生周期1-2-1黏滯運動，具體分析過程與上述一致。

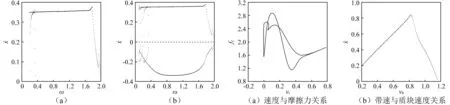
圖2 黏滑運動分岔圖圖3 帶速與摩擦力和質塊速度的關系(ω=1.0) Fig. 2 Bifurcation diagrams of the Fig.3 The relationships between belt speed and slip-stick motion friction or mass velocity when ω=1.0

圖4 黏滑運動相圖及時間歷程圖Fig.4 Phase diagrams and history time diagrams of the slip-stick motion

2.2 黏滑顫振運動

選取系統參數二：k2=2.5，ξ1=1.5，ξ2=2.5，d=0.7，p0=1.2，vb=0.2，vs=0.11，μ=0.3，μk=0.3，μs=0.3，fR=10.5，w1=1，w2=1，σ0=100，σ1=10，σ2=1，以激振頻率ω為分岔控制參數，將含改進的LuGre動摩擦模型引進含有分段非光滑接觸的碰撞系統運動，選取質塊速度大于零的部分與擋板碰撞接觸時的Poincaré截面得到系統運動局部分岔圖圖5(a)所示；為了更進一步說明激振頻率ω與質塊速度的分岔關系，將質塊速度小于零的部分取質塊與擋板接觸分離時的Poincaré截面所得分岔圖如圖5(b)所示，由于分岔圖中得不到黏滯和顫振的具體變化情況，關于黏滯和顫振的詳細變化過程有相圖和時間歷程圖表示；圖6(a)呈現出相對速度與動摩擦力的變化關系；圖6(b)展示了帶速vb與質塊速度的分岔關系，結合帶與質塊的相對速度和動摩擦力之間的關系，可得出質塊在速度為零的附近發生顫振。從分岔圖中得出，分岔控制參數在0～2.4內變化時，質塊的運動速度主要集中在零附近，由相圖及時間歷程圖可清晰地看出，質塊在其速度為零時發生顫振及靜止運動狀態。對系統的具體運動過程轉換分析如下，相圖7(a)呈現出系統在控制參數ω=0.2時，質塊的運動狀態在滑移-接觸碰撞-顫振-靜止-滑移之間相互轉換，時間歷程圖7(e)完整地展示出；控制參數的進一步變化，系統的運動過程會更加的復雜，相圖7(b)及時間歷程圖7(f)呈現出質塊在滑移-接觸碰撞-顫振-靜止-黏滯-滑移之間相互轉換，為了更加詳細地闡述系統在諸多運動過程中的轉換，對時間歷程圖7(f)詳細說明，從黏滯結束的A點開始分析質塊的運動轉換過程，黏滯運動結束的A點為質塊被迫與擋板碰撞接觸，速度發生變化，在激振力與摩擦力相互作用下，進入顫振狀態，隨著質塊的受力變化，質塊在顫振結束后從C點進入靜止狀態，靜止運動，隨著時間的變化，簡諧激振力增大，在D點重新將其拉回滑移狀態，質塊滑移運動到E點，此時質塊所受摩擦力大于其它力之和，且運動速度與帶速相等，質塊發生黏滯運動，黏滯運動持續到質塊與擋板發生碰撞接觸在A點結束，表示質塊在一個運動周期內完成了滑移-接觸碰撞-顫振-靜止-黏滯等運動過程的相互轉換；當分岔控制參數ω=3.0時，系統的運動過程在滑移-顫振-碰撞接觸之間相互轉換，如相圖7(c)和時間歷程圖7(g)所示，具體分析過程與上述一致；當分岔控制參數ω=3.5時，系統發生周期1-2-0運動，無黏滯及顫振運動發生，系統的運動過程在滑移-碰撞接觸之間相互轉換。

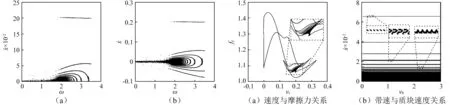
圖5 黏滑顫振運動分岔圖圖6 帶速與摩擦力和質塊速度的關系(ω=0.5) Fig.5 Bifurcation diagrams of the Fig.6 The relationships between belt speed and slip-stick and chattering motion friction or mass velocity when ω=0.5

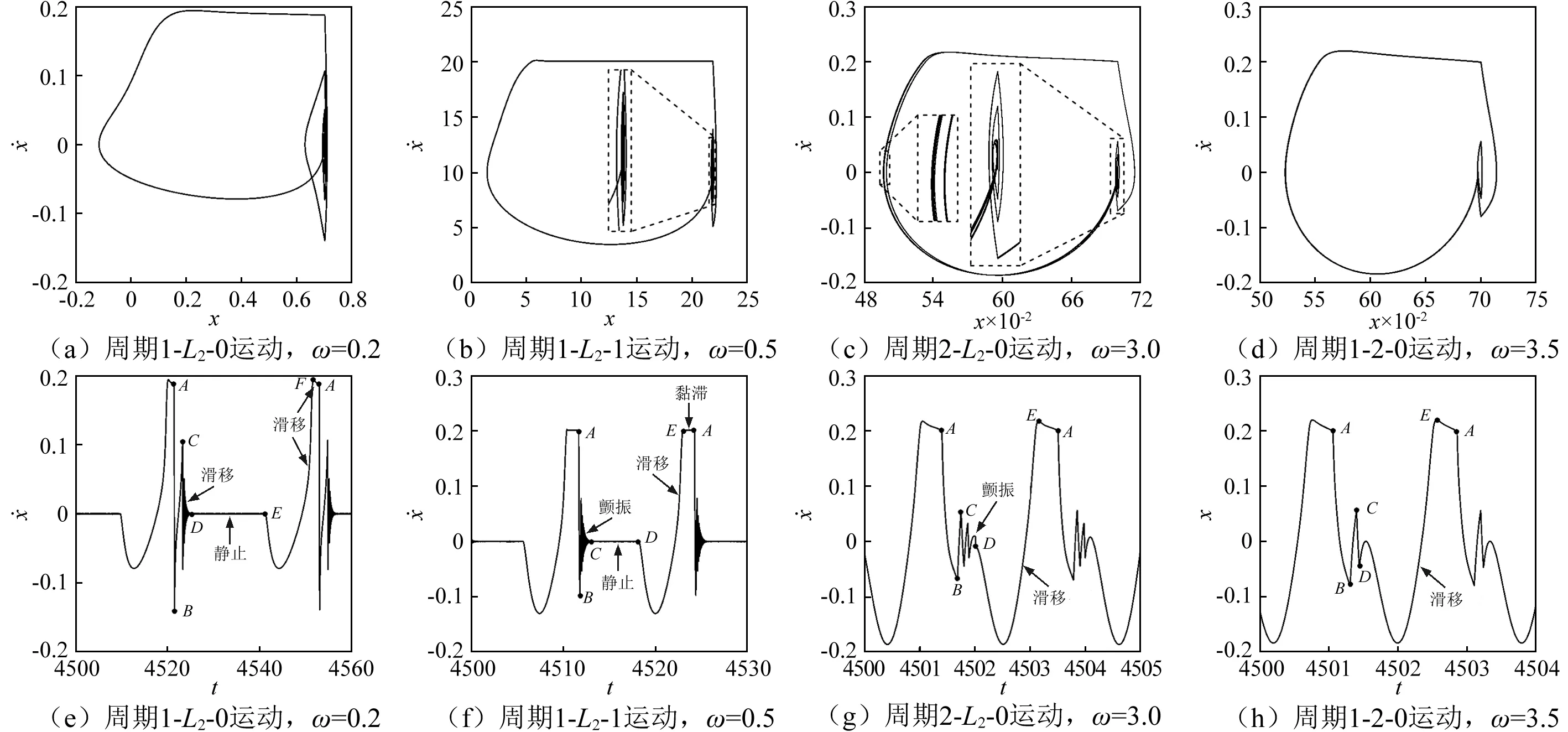
圖7 黏滑顫振運動相圖和時間歷程圖Fig.7 Phase diagrams and time history diagrams of the slip-stick and chattering motion

3 結論

本文建立了一類由含分段阻尼剛度和改進的LuGre動摩擦構成的非光滑振動系統的力學模型，給出了系統的運動方程和不同運動狀態的判斷條件，數值仿真了摩擦誘導振動的動力學現象。主要研究結論如下：

(1)考慮含分段阻尼剛度和改進的LuGre動摩擦后，在一定的系統參數下帶與質塊的相對速度對摩擦力的影響較大。

(2)在一定的系統參數下，系統系統在低頻區域存在滑移-碰撞接觸的運動過程向滑移-黏滯-碰撞接觸或者滑移-黏滯-顫振-碰撞接觸的運動過程轉換現象，系統參數的變化使系統的動力學行為變得非常復雜。

因此，通過本文的研究可以根據需要調整系統參數(改變部分系統結構)使系統工作在一定的運動狀態，如避免發生顫振或黏滯運動等，從而為系統的運動過程控制和結構優化設計提供一定的依據。在低頻下系統運動過程中極易出現黏滯及顫振運動。

[ 1 ] CONE K M, ZADOKS R I. A numerical study of an impact oscillator with the addition of dry friction [J]. Journal of Sound and Vibration, 1995, 188(5): 659-683.

[ 2 ] LUO G W, Lü X H,MA L. Periodic-impact motions and bifurcations in dynamics of a plastic impact oscillator with a frictional slider [J]. European Journal of Mechanics-A/Solids, 2008, 27(6): 1088-1107.

[ 3 ] SOOBBARAYEN K, BESSET S, SINOU J J. Noise and vibration for a self-excited mechanical system with friction [J]. Applied Acoustics, 2013, 74(10): 1191-1204.

[ 4 ] LICSK G, CSERNK G. On the chaotic behaviour of a simple dry-friction oscillator [J]. Mathematics and Computers in Simulation, 2014, 95(1): 55-62.

[ 5 ] ANDREAUS U, CASINI P. Friction oscillator excited by moving base and colliding with a rigid or deformable obstacle [J]. International Journal of Non-Linear Mechanics, 2002, 37(1): 117-133.

[ 6 ] XU L, LU M W, CAO Q. Bifurcation and chaos of a harmonically excited oscillator with both stiffness and viscous damping piecewise linearities by incremental harmonic balance method [J]. Journal of Sound and Vibration, 2003, 264(4): 873-882.

[ 7 ] XU L, LU M W, CAO Q. Nonlinear vibrations of dynamical systems with a general form of piecewise-linear viscous damping by incremental harmonic balance method [J]. Physics Letters A, 2002, 301(1/2): 65-73.

[ 8 ] 丁旺才, 張有強. 干摩擦對碰撞振動系統周期運動的影響分析[J]. 振動與沖擊, 2009, 28(6):110-112.

DING Wangcai, ZHANG Youqiang. Analysis of dry friction on vibro-impact system period motion effect [J]. Journal of Vibration and Shock, 2009, 28(6): 110-112.

[ 9 ] 錢大帥, 劉占生, 劉鎮星,等. 干摩擦質塊雙黏著運動響應的級數形式解及黏滑邊界分析[J]. 振動與沖擊, 2013,32(9): 73-78.

QIAN Dashuai, LIU Zhansheng, LIU Zhenxing, et al. Series solution of double-stick motion response of dry friction oscillator and stick-slip boundary analysis [J]. Journal of Vibration and Shock, 2013,32(9): 73-78.

[10] LIU Y, EKATERINA P, MARIAN W, et al. Forward and backward motion control of a vibro-impact capsule system [J]. International Journal of Non-Linear Mechanics, 2015, 70(4): 30-46.

[11] DE WIT C C, OLSSON H, ASTROM K J, et al. A new model for control of systems with friction [J]. IEEE Transactions Automatic Control, 1995,40(3): 419-425.

[12] HOFFMANN N P. Linear stability of steady sliding in point contacts with velocity dependent and LuGre type friction [J]. Journal of Sound and Vibration, 2007,301(3/4/5): 1023-1034.

[13] SAHA A, WAHI P. An analytical study of time-delayed control of friction-induced vibrations in a system with a dynamic friction model [J]. International Journal of Non-Linear Mechanics, 2014, 63(1/2/3/4): 60-70.

[14] SAHA A, WIERCIGROCH M, JANKOWSKI K, et al. Investigation of two different friction models from the perspective of friction-induced vibrations [J]. Tribology International, 2015, 90(10): 185-197.