地震動參數對土坡地震響應的影響權重研究
張江偉, 李小軍, 齊劍峰, 王玉石, 賀秋梅
(1.河北地質大學 勘查技術與工程學院,石家莊 050031;2.中國地震局 地球物理研究所,北京 100081)
地震誘發滑坡是一種常見的地震次生地質災害,在居民集中的山區發生強烈地震后,地震觸發的滑坡的危害性往往比地震直接造成的災害還要大[1]。2008年發生在我國四川省汶川縣的Ms8.0級大地震觸發了大規模的山體滑坡、崩塌等地質災害,吞沒了大量當地居民的家園,給人類生命、財產安全和社會可持續發展帶來了巨大的損害。
研究地震作用下邊坡穩定性問題時,由于地震動存在隨機性,所以地震動強度指標的選取是首要解決的問題。長久以來,地震動峰值加速度和地震動峰值速度一直被地震工程學家和工程師認為是能夠表征地震動潛在破壞勢的參數。現有的相關研究已有不少,如文獻[2-10]等均采用了地震動峰值加速度作為主要強度指標對邊坡動力問題進行了研究分析。王秀英等[11]收集了汶川地震誘發的近3 000個滑坡資料和記錄到的地震動數據,對地震誘發滑坡與地震動峰值速度的關系進行了研究分析,發現地震誘發滑坡與地震動峰值速度(Peak Ground Velocity, PGV)存在明顯的正相關性,可以利用PGV作為判別地震滑坡的判據;Saygili等[12]利用了地震動峰值加速度(Peak Ground Acceleration,PGA)和地震動峰值速度(PGV)兩個參數來預測坡體的滑動位移。我國劉恢先在上世紀為編制中國地震烈度表曾將PGA和PGV分別與烈度進行了相關性分析,結果顯示這兩個參數都和烈度有很好的相關性。除此之外,也有學者展開地震動持時和頻譜特性對邊坡動力穩定性影響的研究,如徐光興等[13]選用不同地震動峰值加速度、持時以及頻譜參數,對邊坡動力響應的影響規律進行了研究分析,結果表明坡面加速度峰值放大系數隨輸入地震波振幅、頻率的增加而減小,持時對加速度峰值響應的影響不大,坡體位移隨振幅、持時的增加而顯著增大,隨頻率的增大而減小。閆坤伐等[14]也對地震動加速度振幅、頻譜及持時對邊坡動力響應的影響規律做了研究。
縱觀目前研究,全面地對地震動各參數影響權重的研究較少,導致在分析邊坡地震動力穩定性時,地震動參數的選取尚不統一。基于以上背景,本文選取100條具有不同峰值加速度(PGA)、峰值速度(PGV)、阿里亞斯強度(Arias Intensity,AI)、絕對累積速度(Cumulative Absolute Velocity,CAV)、持時和特征周期的地震動記錄,計算并分析了各強度指標與邊坡動力響應的相關性,得到各參數的影響權重,為邊坡地震動力響應分析提供地震動參數選用的基礎和依據。
1 計算方法
1.1 有限元法
在研究分析地震作用下邊坡穩定性問題時,有限元數值模擬方法采用實際的地震動輸入,真實反映坡體在地震下的動力響應特性,且不受邊坡地質條件、幾何形態等因素的限制,可以解決難以用解析法求解的問題,更加實際合理地評價地震作用下邊坡動力穩定性。因此有限元數值模擬方法在解決邊坡地震穩定性問題中得到了廣泛而深入地應用。
有限元法是把結構模型離散為有限個單元體,單元體在受到地震荷載作用時,運用考慮單元體慣性和阻尼因素影響的動力力學平衡方程來求解。動力力學平衡方程可表達為式(1)
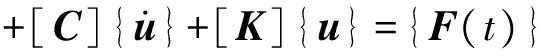
(1)
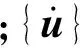
對于求解地震作用下的動力問題,動力荷載就是地震荷載,于是求解邊坡地震動力穩定性問題的基本力學運動方程可寫為
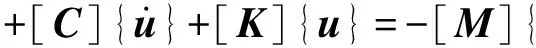
(2)
式中:{üg(t)}為地震動加速度時程。
1.2 相關性計算方法
在邊坡地震穩定性評價中,合理的地震動強度指標應能突出反映邊坡地震響應的程度。本文通過Pearson相關系數來確定地震動各參數對邊坡地震響應的影響權重,從而得到評價邊坡地震穩定性的合理參數。Pearson相關系數是英國統計學家皮爾遜于19世紀80年代提出的一種計算兩個變量之間相互關系的指標,范圍在-1.0~1.0的無量綱指數,用來考察兩個事物之間相關程度的強弱。隨后在學術研究中被廣泛地用于兩因素之間相關程度的計算[15]。具體計算過程如下:
步驟1 將第i條地震動的某一地震動強度指標值記為Ii;
步驟2 采用有限元法計算邊坡模型在第i條地震動輸入下的邊坡最大地震響應值Ri;
步驟3 重復步驟1和步驟2,得到所有地震動記錄的Ri及其對應的Ii;
步驟4 將所有地震動的計算結果畫在R-I坐標系中,并通過式(3)計算得到R與I之間的pearson相關系數r。
(3)
式中:r為各地震動參數的影響權重,r越接近1.0,則說明其相關性越好,即用該地震動強度指標來計算邊坡地震響應就越合理。
2 模型建立及計算參數
2.1 模型建立
為研究邊坡在地震作用下的動力響應特性,建立如圖1的二維土坡模型。并沿土坡坡面處布設5個觀測點。模型長×高=170 m×70 m,邊坡坡角為34°,坡高30 m,邊坡坡頂后緣長為80 m。根據Lysmer等[16]的研究成果,巖土體模型網格尺寸受輸入地震波的最短波長控制,網格最大尺寸應小于最短波長的1/8~l/10。本構模型為理想彈塑性本構模型,屈服準則采用適用于巖土體的力學行為的摩爾-庫侖強度準則。為充分研究邊坡在地震作用下的響應規律,模型材料假定為均質材料,邊坡土體的力學參數見表1。
對模型進行靜力計算獲得自重應力場并平衡后,進行邊坡地震動力響應計算。在模擬分析邊坡等半無限體的動力問題時,為了防止地震波傳播到模型邊界處反射回模型,通常需要設置人工邊界來實現必要的能量發散[17],因此模型邊界設置黏彈性邊界,即在邊界處設置彈簧和阻尼單元。模型的阻尼采用工程中常用的Rayleigh阻尼形式。
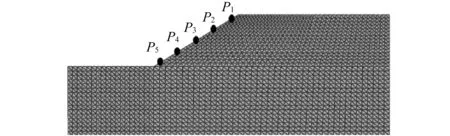
圖1 邊坡模型示意圖Fig.1 Finite element mesh

參數密度/(kg·m-3)彈性模量/MPa泊松比黏聚力/kPa內摩擦角/(°)數值207090.80.313.9925
2.2 地震動選取
本文從太平洋地震研究中心數據庫里共隨機選取了100條具有不同地震動參數特性的原始地震動記錄,并分別對各條地震動記錄進行積分、傅里葉變換等計算處理以統計其PGA、PGV、阿里亞斯強度(AI)、累積絕對速度(CAV)、持時和特征周期。經計算可知,所選取的地震動記錄中加速度峰值PGA變化范圍為0.004 1~1.225 9g,PGV范圍為0.378~112.376 cm·s-1,阿里
亞斯強度范圍為0.000 4~8.887 9 m·s-1,CAV 范圍為0~0.285 7 g·s,持時[18]的范圍為0.21~46.12 s,特征周期范圍為0.09~2.00 s。由此可見,這100條地震動的參數變化范圍較大,具有較大的隨機性。本文將上述每條原始地震動記錄進行基線矯正后作為輸入來計算邊坡的響應,進而展開對地震動不同強度指標影響權重的研究分析。
3 結果分析
將以上處理后的100條地震動記錄作為輸入,模擬計算邊坡的地震響應。本文將邊坡觀測點的最終變形位移和坡頂輸出加速度作為邊坡響應的代表值來研究地震動各參數對邊坡地震響應的影響。
3.1 地震動參數的影響規律
提取邊坡5個觀測點在各地震動作用下的最終位移和坡頂處P1點的加速度放大系數,研究其隨地震動峰值加速度(PGA)、地震動峰值速度(PGV)、阿里亞斯強度(AI)、絕對累積速度(CAV)、持時和特征周期的變化規律。限于篇幅,且結果顯示變化規律相似,本文只列出了坡頂處P1點的最終變形位移和加速度放大系數隨地震各參數的變化規律,如圖2~圖7所示。
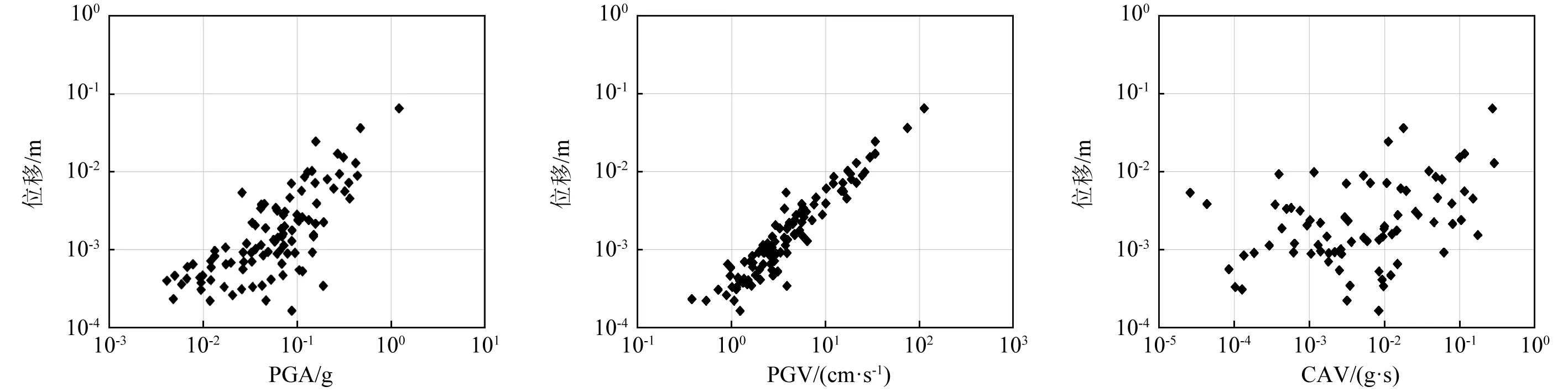
圖2 P1點變形位移隨PGA的變化 圖3 P1點變形位移隨PGV的變化 圖4 P1點變形位移隨CAV的變化Fig.2 Variation of P1 displacement with PGA Fig.3 Variation of P1 displacement with PGV Fig.4 Variation of P1 displacement with CAV

圖5 P1點變形位移隨阿里亞斯強度的變化 圖6 P1點變形位移隨地震動持時的變化 圖7 P1點變形位移隨地震動特征周期的變化 Fig.5 Variation of P1 displacement with Fig.6 Variation of P1 displacement Fig.7 Variation of P1 displacement Arias intensity with duration with characteristic period
由圖2~圖7可知,坡體變形位移響應對各地震動參數的敏感度存在顯著差異,在整體上隨著地震動峰值速度(PGV)、地震動峰值加速度(PGA)和阿里亞斯強度(AI)呈現增大而增大的變化規律,表明以這三個指標的強弱均可以來描述地震對斜坡穩定性的影響程度。同時坡體變形位移對三者變化的敏感度有所不同,其中地震動峰值速度(PGV)與坡體變形位移響應存在著明顯的相關性,兩者分布均勻且近乎成斜直線。而地震動絕對累積速度(CAV)、持時和特征周期值與坡體變形位移的分布較為雜亂,似乎也存在著一定正相關性,但影響規律不明顯。
由圖8~圖13可知,不同地震動作用下坡頂加速度放大系數整體僅隨著地震動持時和特征周期的變化呈現出一定的規律,表現出較強正相關性,即隨著地震動持時和特征周期的增大,坡頂加速度放大系數總體也是增大的。但當地震動特征周期大于1.7 s時,坡頂加速度放大系數呈現出逐漸減小的趨勢。地震動峰值加速度(PGA)、地震動峰值速度(PGV)、阿里亞斯強度(AI)以及絕對累積速度(CAV)對坡頂加速度放大系數的影響則較小,表現出的規律性不強。
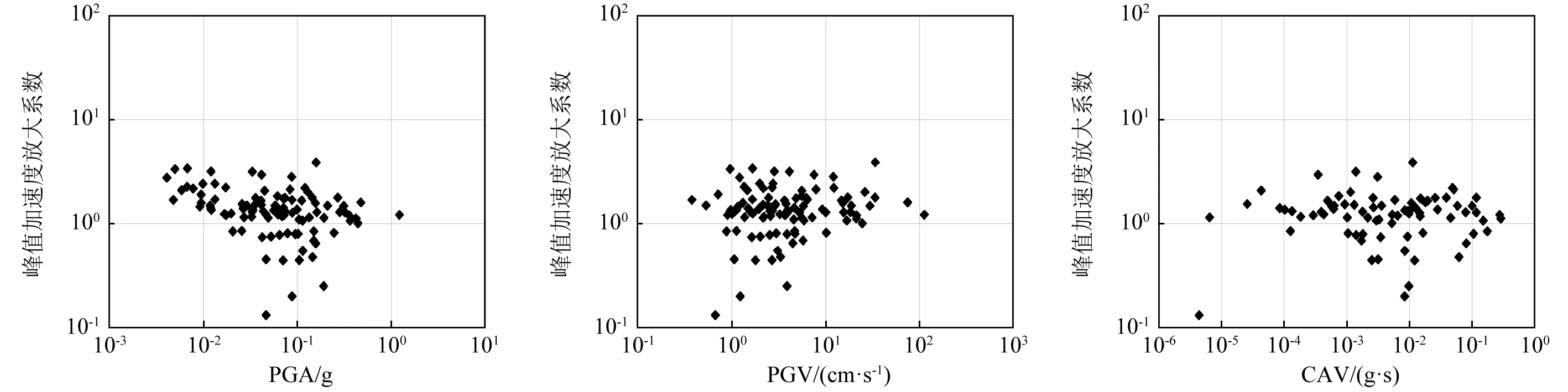
圖8 P1點加速度放大系數隨PGA的變化 圖9 P1點加速度放大系數隨PGV的變化 圖10 P1點加速度放大系數隨CAV的變化 Fig.8 Variation of P1 displacement Fig.9 Variation of P1 PGA amplification Fig.10 Variation of P1 PGA amplification with PGA coefficients with PGV coefficients with CAV
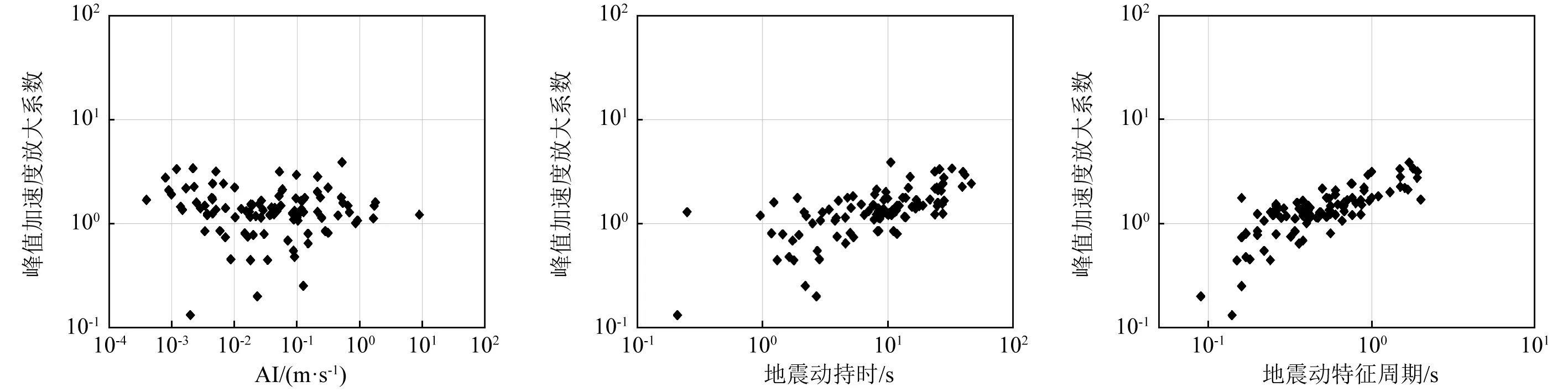
圖11 P1點加速度放大系數隨阿里亞斯 圖12 P1點加速度放大系數隨地震 圖13 P1點加速度放大系數隨地震 強度的變化 動持時的變化 動特征周期的變化 Fig.11 Variation of P1 PGA amplification Fig.12 Variation of P1 PGA amplification Fig.13 Variation of P1 PGA amplification coefficients with Arias intensity coefficients with duration coefficients with characteristic period
3.2 地震動參數影響權重性研究
上述分析表明地震動各參數對邊坡地震響應的影響程度是不同的。為進一步研究分析各參數對邊坡地震響應的影響敏感度,本文計算了邊坡各位移監測點在不同地震動作用下的最終位移和坡頂加速度放大系數與地震動峰值加速度(PGA)、地震動峰值速度(PGV)、阿里亞斯強度(AI)、絕對累積速度(CAV)、持時和特征周期值的相關系數,如表2所示。
通過對上表中相關性計算的結果進行研究分析,可以認為:
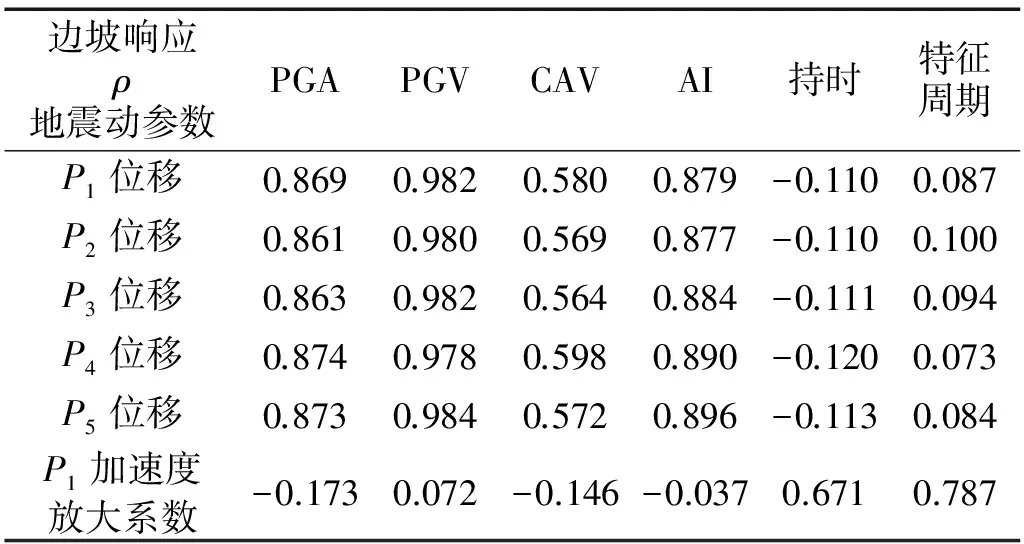
表2 地震動參數和邊坡地震響應的相關系數
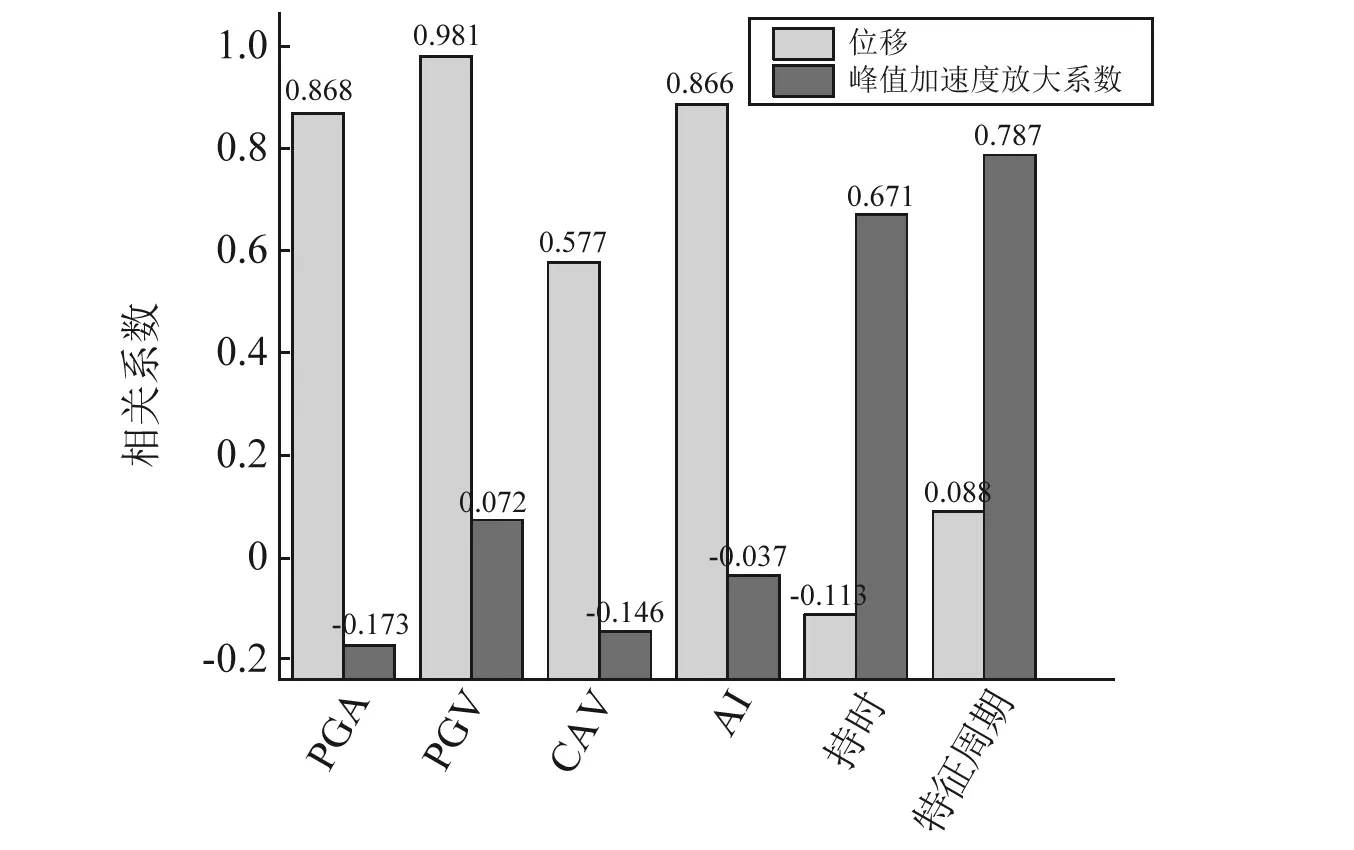
圖14 地震動參數與土坡變形位移和加速度放大系數的相關系數Fig.14 The correlation coefficient between slope seismic response and ground motion parameters
地震動峰值速度(PGV)與坡體五個位移監測點的響應的相關性最高,相關系數在0.979~0.985,平均值為0.981,接近于1。地震動速度與質點運動的能量是具有直接關系的,因而PGV可以在一定程度上反映震時地表震動釋放能量的強度,也就決定了對土坡作用的大小;其次為阿里亞斯強度(AI),相關系數在0.877~0.896,平均值為0.886。由于阿里亞斯強度是一個綜合了地震動中所有震動幅值和持時的指標,因此它更好地表征震動釋放的能量對土坡響應的影響程度;地震動峰值加速度(PGA)對土坡位移響應的相關程度僅次于阿里亞斯強度(AI),其相關系數在0.861~0.874,平均值為0.868。PGA是目前工程中被運用最為廣泛的一個指標,獲取較為方便,且很大程度上可以描述地震動的強弱,但由于峰值加速度具有隨機的特點,離散性很大,而且會發生臨近震中或斷層的飽和現象[19],例如處于高頻上的加速度峰值則對土坡的影響則較小,因此將PGA作為強度指標來研究土坡穩定性時應考慮地震動的頻譜特性。絕對累積速度(CAV)是潛在破壞作用的地面加速度絕對值在整個地震時間歷程上的積累,多用于核電結構的地震分析中,與土坡位移響應的相關系數在0.564~0.598,平均值為0.577,相比之下兩者相關程度不是很高。而持時和特征周期與土坡位移響應的相關系數則更低,即它們的大小對土坡位移的影響相對較小。
(2)坡頂加速度放大系數與地震動特征周期和持時有著較高的相關性,相關系數分別為0.787和0.671。其中特征周期的相關系數最高,這可以用共振現象來解釋。而地震動峰值加速度(PGA)、地震動峰值速度(PGV)、阿里亞斯強度(AI)和絕對累積速度(CAV)四個指標對其相關程度則較低。
4 結 論
計算分析了土坡在多組地震動作用下的動力響應,得到了地震動峰值加速度(PGA)、地震動峰值速度(PGV)、阿里亞斯強度(AI)、絕對累積速度(CAV)、持時和特征周期對土坡位移和加速度放大系數的相關系數,通過探討其相關性和影響規律,得到以下結論:
(1)對于土坡坡面的變形位移響應,與其相關性較高的三個參數依次為地震動峰值速度(PGV)、阿里亞斯強度(AI)和地震動峰值加速度(PGA),其平均相關系數分別為0.981、0.886、0.868,且均呈現正相關現象。絕對累積速度(CAV)、持時和特征周期也對土坡坡面位移響應有一定的影響,但是敏感度相對較低。因此在選用地震參數指標研究土坡地震響應或災害評估時應優先考慮地震動峰值速度(PGV)、阿里亞斯強度(AI)和地震動峰值加速度(PGA)這個強度指標。
(2)對于土坡坡頂加速度響應,與其相關性較高的兩個參數依次為地震動的特征周期和持時,相關系數分別為0.787和0.671,呈現正相關現象。但當特征周期超過1.7 s時,此時地震對土坡作用減小,因此坡頂加速度放大系數出現逐漸下降的趨勢。其他地震動參數對土坡坡頂加速度響應的影響相對較小。
[ 1 ] 李忠生.國內外地震滑坡災害研究綜述[J].災害學,2003,18(4):64-70.
LI Zhongsheng. The state of the art of the research on seismic landslide hazard at home and abroad[J]. Journal of Catastrophology, 2003, 18 (4):64-70.
[ 2 ] HARP E L, WILSON R C. Shaking intensity thresholds for rock falls and slides: evidence from 1987 Whittier Narrows and Superstition Hills earthquake strong-motion records[J]. Bulletin of the Seismological Society of America ,1995,85(6): 1739-1757.
[ 3 ] WILSON R C, KEEFER D K. Predicting areal limits of earthquake-induced landsliding[M]∥Evaluating Earthquakes Hazards in the Los Angeles Region—an Earth-Science Perspective. Washington: USGS Professional,1985:317-345.
[ 4 ] 祁生文,伍法權,孫進忠,等.邊坡動力響應規律研究[J].中國科學E輯,2003,33(增刊1):28-40.
QI Shengwen, WU Faquan, SUN Jinzhong. Study on the dynamic response characteristic of slope[J].Science in China, Ser. E, 2003, 33 (Sup 1): 28-40.
[ 5 ] 殷躍平.汶川八級地震滑坡特征分析[J].工程地質學報, 2009, 17(1): 29-38.
YIN Yueping. Features of landslides triggered by the 8.0 Wenchuan earthquake[J]. Journal of Engineering Geology, 2009, 17(1): 29-38.
[ 6 ] 王秀英,聶高眾,王登偉,等.汶川地震誘發滑坡與地震動峰值加速度對應關系研究[J].巖石力學與工程學報,2010,29(1):82-89.
WANG Xiuying, NIE Gaozhong, WANG Dengwei. Research on relationship between landslides and peak ground accelerationsinduced by Wenchuan earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):82-89.
[ 7 ] 言志信,張森,張學東,等.順層巖質邊坡地震動力響應及地震動參數影響研究[J]. 巖石力學與工程學報,2011, 30(增刊2): 3522-3528.
YAN Zhixin, ZHANG Sen, ZHANG Xuedong, et al. Study of dynamic response of bedding rock slope under earthquake and influence of ground motion parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Sup2): 3522-3528.
[ 8 ] 李海波,肖克強,劉亞群,等.地震荷載作用下順層巖質邊坡安全系數分析[J].巖石力學與工程學報,2007,26(12):2385-2394.
LI Haibo, XIAO Keqiang, LIU Yaqun,et al. Factor of safety analysis of bedding rock slope under seismic load[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2385-2394.
[ 9 ] 楊崢,許強,劉漢香,等.地震作用下含反傾軟弱夾層斜坡的動力變形破壞特征研究[J].振動與沖擊,2014,33(19):134-139.
YANG Zheng, XU Qiang, LIU Hanxiang, et al. Dynamic deformation and failure of slopes with an anti-dip weak interlayer under earthquakes[J]. Journal of Vibration and Shock,2014,33(19): 134-139.
[10] 梁雙慶,蘇立君,王洋.不同坡面角度碎石土斜坡動力響應特征研究[J].振動與沖擊,2016,35(21):153-158.
LIANG Shuangqing, SU Lijun, WANG Yang. Dynamic response characteristics of gravel soil slope with different angles of inclination[J]. Journal of Vibration and Shock, 2016, 35(21): 153-158.
[11] 王秀英,王登偉.四川汶川地震誘發滑坡與峰值速度的關系[J].地質通報, 2011, 30(1) : 159-165.
WANG Xiuying, WANG Dengwei. Relationships between the Wenchuan earthquake-induced landslide and peak ground velocity, Sichuan, China[J]. Geological Bulletin of China,2011,30(1): 159-165.
[12] SAYGILI G, RATHJE E M. Probabilistically based seismic landslide hazard maps: an application in Southern California[J]. Engineering Geology,2009,109(3/4):183-194.
[13] 徐光興, 姚令侃, 李朝紅, 等.邊坡地震動力響應規律及地震動參數影響研究[J].巖土工程學報,2008,30(6): 918-923.
XU Guangxing, YAO Lingkan, LI Zhaohong, et al. Dynamic response of slopes under earthquakes and influence of ground motion parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 30(6):918-923.
[14] 閆坤伐,盧建華,劉曉燕,等.地震作用下高邊坡破壞的振動臺試驗[J].鐵道科學與工程學報,2016,13(12):2396-2404.
YAN Kunfa, LU Jianhua, LIU Xiaoyan, et al. Shaking table test for high slope destruction under earthquake action[J].Journal of Railway Science and Engineering,2016,13(12):2396-2404.
[15] 李雪紅,李曄暄,吳迪,等.地震動強度指標與結構地震響應的相關性研究[J].振動與沖擊,2014,33(23):184-189.
LI Xuehong, LI Yexuan, WU Di, et al. Correlation between ground motion intensity and structural seismic response[J]. Journal of Vibration and Shock,2014,33(23):184-189.
[16] LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media[J].Journal of Engineering Mechanics, ASCE, 1969, 95(4): 859-877.
[17] 李小軍,廖振鵬,杜修力.有阻尼體系動力問題的一種顯式差分解法[J].地震工程與工程振動,1992,9(4):74-80.
LI Xiaojun, LIAO Zhenpeng, DU Xiuli. An explicit finite difference method for viscoelastic dynamic problem[J]. Journal of Earthquake Engineering and Engineering Vibration, 1992, 9(4): 74-80.
[18] 胡聿賢.地震工程學[M].2版.北京:地震出版社,2006:104-109.
[19] 李小軍,彭青,劉文忠.設計地震動參數確定中的場地影響考慮[J].世界地震工程, 2001, 17(4):34-41.
LI Xiaojun, PENG Qing, LIU Wenzhong. Consideration of site effects for determination of design earthquake ground motion parameters[J]. World Earthquake Engineering,2001,17(4):34-41.

