Pekeris水聲波導(dǎo)環(huán)境中聲壓信號采樣時段對船舶聲源級評定的影響研究

鄒明松, 劉樹曉

(1.中國船舶科學(xué)研究中心，江蘇 無錫 214082； 2.深海載人裝備國家重點實驗室，江蘇 無錫 214082；3.船舶振動噪聲重點實驗室，江蘇 無錫 214082)

在實際海洋水聲環(huán)境中，如何科學(xué)地評定一艘船舶的水下輻射噪聲量值是工程中十分關(guān)注的、存在一定爭議的問題，是一個較為復(fù)雜的聲學(xué)問題，涉及到海洋背景下的信噪比、船舶周圍的近場和遠場聲分布、聲壓信號的采集與處理方法、船舶所處的海洋環(huán)境水聲傳播規(guī)律以及船舶航速和潛深等諸多因素。國內(nèi)外建有一批各具特色的船舶水下輻射噪聲測試試驗場及配有相應(yīng)的測試規(guī)程，采用單水聽器、線陣等方式測試評定船舶的輻射噪聲[1-2]。當采用單水聽器測試時，如何選取聲壓信號的采樣時段對聲源級的換算評定有較顯著影響，國內(nèi)外并無統(tǒng)一的標準。目前，為便于工程上的實際操作，在實船測試中往往截取信號能量最強的特定長度(如8 s左右)的聲壓時域測試數(shù)據(jù)，通過Fourier變換獲取與該時間段對應(yīng)的輻射噪聲頻譜，再換算出聲源級。這種測試處理方式是工程經(jīng)驗性的，其科學(xué)性如何，并無較強的理論根據(jù)，更沒有通過仿真計算進行過規(guī)律性的定量分析和總結(jié)。整體而言，這是一個需要通過計算研究去指導(dǎo)工程操作、優(yōu)化工程操作的問題，是一個值得關(guān)注和探討的問題，但目前未見有深入的研究和報道。

國內(nèi)已具備開展復(fù)雜船舶結(jié)構(gòu)流固耦合振動與水下聲輻射大規(guī)模仿真計算的能力[3-4]，這為針對上述問題開展計算研究提供了很好的基礎(chǔ)。特別是近年來，人們發(fā)現(xiàn)海洋水聲環(huán)境對船舶周圍的輻射聲場存在不可忽略的影響，將浮體結(jié)構(gòu)水中聲輻射的計算研究，從無界理想聲介質(zhì)環(huán)境拓展到近似考慮水面和水底邊界影響的聲場環(huán)境[5-6]。Zou等[7-8]將船舶三維水彈性力學(xué)理論與水聲信道理論相結(jié)合，建立了船舶三維聲彈性理論，為開展海洋水聲環(huán)境中船舶流固耦合振動、聲輻射與聲傳播的統(tǒng)一分析提供了一種前所未有的方法，且理論上具有較廣泛的適用性。在船舶三維聲彈性理論基礎(chǔ)上開發(fā)出的THAFTS-Acoustic軟件，其準確性和實用性經(jīng)過數(shù)值算例與試驗的多重考核驗證，已經(jīng)可以方便地實現(xiàn)Pekeris水聲波導(dǎo)環(huán)境中船舶流固耦合振動、聲輻射與聲傳播的集成計算[9]。

Pekeris水聲波導(dǎo)模型是一種較常用的淺海水聲環(huán)境模型，能夠較好地反應(yīng)淺海水聲環(huán)境的特點。因此，采用現(xiàn)有的船舶三維聲彈性計算方法及THAFTS-Acoustic軟件，能夠計及海面和海底邊界的影響，對淺海中的實船測試問題進行較準確的仿真計算，為本文中所述問題的研究提供了優(yōu)良的基礎(chǔ)。本文正是采用該理論方法和軟件，進行建模計算，首次探討了淺海Pekeris水聲波導(dǎo)環(huán)境中用正橫方向的觀察點獲取船舶在機械激勵下的輻射噪聲聲源級時，聲壓信號采樣時間段的影響規(guī)律；首次以定量數(shù)值計算結(jié)果為支撐，給出了有助于更全面地獲取船舶輻射噪聲頻譜特征及使得觀察結(jié)果更加穩(wěn)定的聲壓信號采樣時段選取的指導(dǎo)性建議。

1 計算模型和水聲環(huán)境

假定觀察點位于船體舷側(cè)，離船體軸線的距離小于船長，相對空間固定坐標系靜止。當船舶以航速U勻速沿直線航行時，觀察點相對于船舶以速度U反方向運動，觀察點處的聲壓也隨著船舶的運動而變化。在淺水環(huán)境中，船體周圍的聲場分布與船內(nèi)激勵源分布、船體各部分聲輻射效率和海底、海面聲反射等因素密切相關(guān)。往往在船舶艏部、中部、艉部區(qū)域的聲場分布并不相同，選取不同時間段的聲壓信號(對應(yīng)觀察點相對船體的不同空間位置)換算出的聲源級也將是不同的。如何選取時間信號，能夠較全面的反映船舶的輻射噪聲頻譜特征和噪聲級量值水平，將是本文要探討的內(nèi)容。

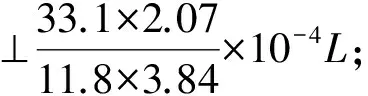
圖1 單層殼船體結(jié)構(gòu)計算模型Fig.1 Computational model of the single shell ship structure

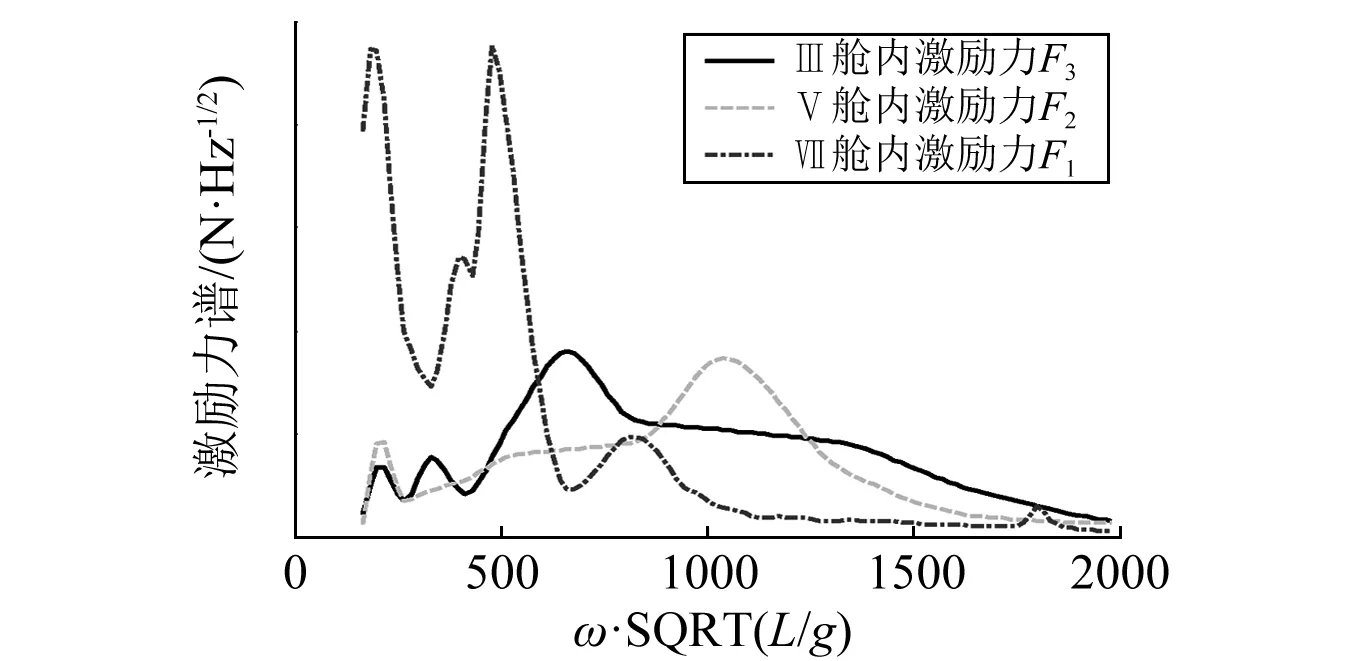
圖2 由3臺典型機械設(shè)備引起的激勵力譜Fig.2 Excitation force spectra induced by three typical mechanical equipments

采用表1所示參數(shù)的Pekeris水聲波導(dǎo)計算環(huán)境(見圖3)，分析選取不同采樣時段的聲壓信號對船舶聲源級評定的影響。表中海底聲學(xué)參數(shù)的取值與某淺海海域的聲學(xué)參數(shù)較接近，聲波垂直入射到海底時的聲反射系數(shù)為0.465 2。表中的潛深是指船體重心離水面的距離。

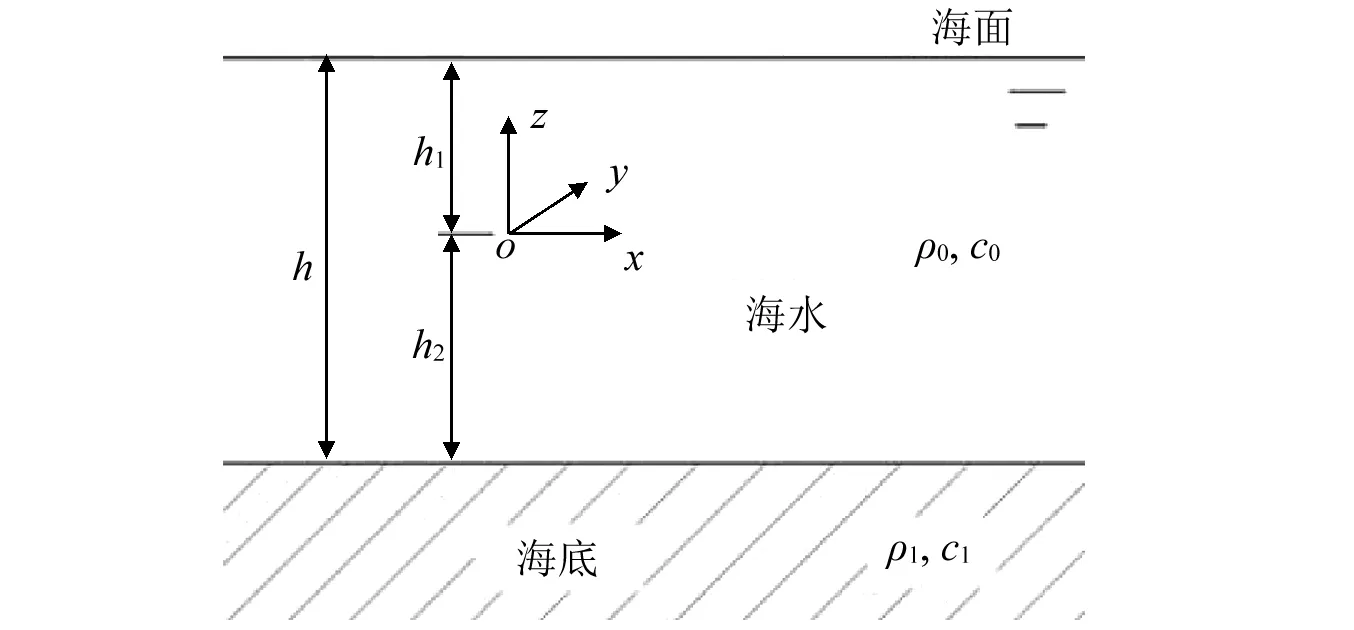
圖3 具有壓力釋放海面和可透聲液體海底的Pekeris波導(dǎo)Fig.3 Pekeris waveguide with boundary release sea surface and liquid seabed allowing sound transmission

水深潛深海水密度ρ0海水聲速c0海底密度ρ1海底聲速c165m30m1025kg/m31500m/s2600kg/m31620m/s

2 計算分析的基本方法

圖1中的模型以6 kn速度沿直線航行，在左舷設(shè)置兩個固定不動的觀察場點，離船體軸線的距離分別為0.5L和0.8L，且都在船體縱軸線所處的水平面內(nèi)，見圖4所示，其中的3個圓點對應(yīng)圖2所示的3個集中力作用點。從相對運動的角度進行分析，可將船看成靜止，觀察點運動，整個聲壓信號是在一條直線段上測得的，直線段上的每一點具有相對于船體的不同空間位置，如圖4中的“1號觀察點相對平移線”和“2號觀察點相對平移線”。

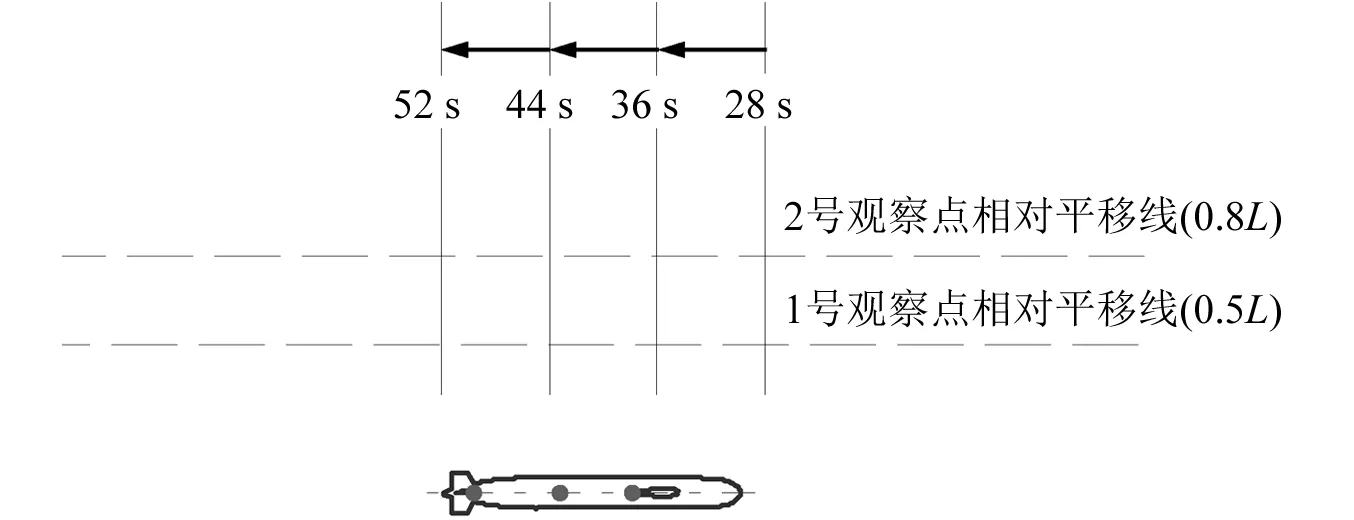
圖4 相對運動觀察點對應(yīng)的計算工況示意圖Fig. 4 A sketch of the computation cases corresponding to the observation points for relative motion

采用表1中的環(huán)境參數(shù)，使用THAFTS-Acoustic軟件計算出觀察點相對平移線上各場點的頻域聲壓結(jié)果。考慮到觀察點的位置相對于船舶在移動，在每一個采樣時刻，必須采取觀察點到新位置x-Ut處該時刻的聲壓值，因此，有必要將頻域聲壓的幅值與相位譜轉(zhuǎn)化到時域中，此時的聲壓公式為

cos{ωnt+arg[p(x-Ut,y,z,ωn)]}

(1)

式中：t為時間；U為船舶航速；(x-Ut,y,z)為觀察點的空間坐標，相對于隨船運動的平衡坐標系，它隨時間t變化；p(x-Ut,y,z,ωn)為空間坐標(x-Ut,y,z)點處角頻率ωn處的聲壓譜值，由激勵力譜與聲輻射傳遞函數(shù)相乘得到；Δω=ωn+1-ωn；arg[]為取相位角。

本文選取聲壓最強的時間段換算輻射噪聲級(這是實船測試中較常采用的方法)，先考慮取該時間段為8 s。總的時域計算的區(qū)間為0～81 s，相當于船舶移動了250 m。計算(tn～tn+8)時間段內(nèi)的聲壓均方根值，其中tn=0,1,…，73，通過比較聲壓均方根值的大小，確定用于換算輻射噪聲級的tn取值。再通過加窗Fourier變換并結(jié)合重疊平均的韋爾奇(Welch)方法計算功率譜，得出頻域內(nèi)的聲壓譜值，再轉(zhuǎn)化成距船體軸線1 m遠處的聲源級(聲壓參考值為1×10-6Pa)。

3 不同的8 s采樣時段對換算聲源級的影響

圖5給出了兩個觀察點處的時域聲壓曲線。圖6給出了不同8 s長時間段對應(yīng)的聲壓均方根值(其中縱坐標表示的聲壓均方根值已相對最大值作了歸一化)，可用于確定換算輻射噪聲級的tn取值。綜合考慮圖6所示的兩個觀察點的聲壓均方根曲線之后，確定選取tn=28、35、39，亦即28～36 s、35～43 s和39～47 s這3個時間段信號，通過Fourier變換計算聲壓頻譜，轉(zhuǎn)化成距船體軸線1 m遠處的聲源級，結(jié)果如圖7所示。可見：取不同8 s時間段信號換算出的聲源級存在一定差異；圖中A、B、C3個峰值處的差異也較明顯，最大達到7.4～8.0 dB；且不同時間段對應(yīng)的最高峰值頻率也不同，說明考察船舶噪聲時，如選定較固定的8 s時間段(觀察點相對移動位置較固定)，則給出的噪聲級頻譜可能會漏掉實際存在的較顯著的峰值特征。

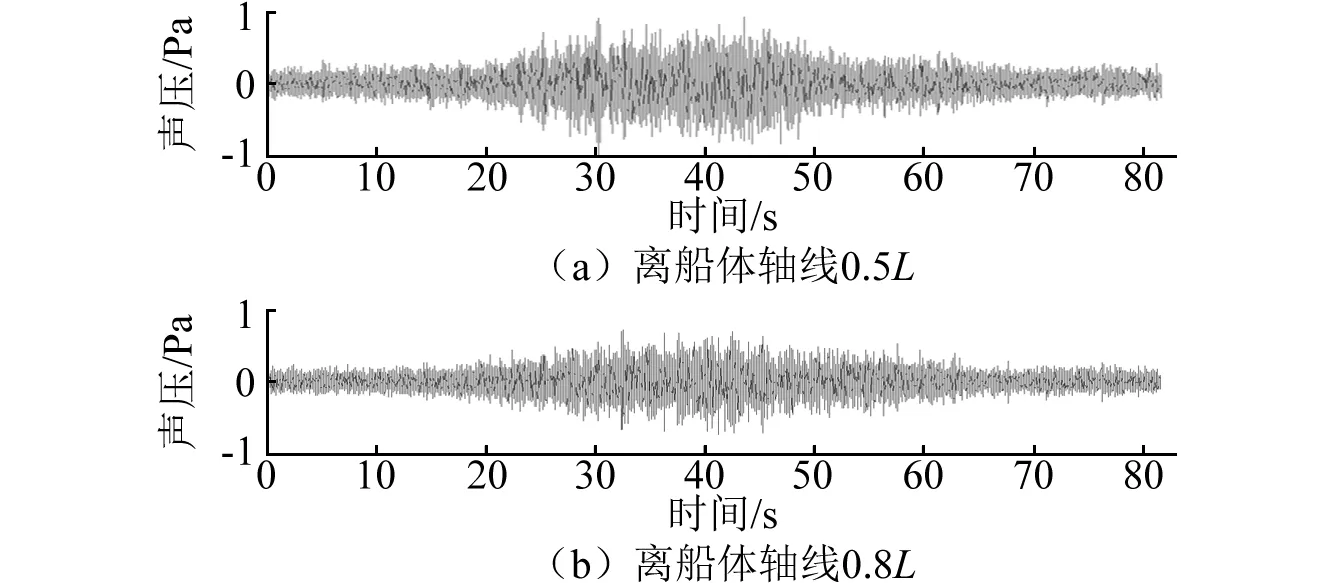
圖5 離船體軸線不同距離的觀察點的時域聲壓曲線Fig. 5 Time domain sound pressure curves at observation points with various distance from the axis of the hull

圖6 兩個觀察點在不同8 s時間段內(nèi) (a)離船體軸線距離為0.5L的觀察點 (b)離船體軸線距離為0.8L的觀察點 的聲壓均方根曲線 換算出的聲源級 換算出的聲源級Fig. 6 Sound pressure rms values of 8 s time 圖7 不同8 s時間段換算出的聲源級結(jié)果 intervals at two observation points Fig. 7 Sound source level transformed from various 8 s time intervals

4 采樣長度對聲源級換算的影響

6 kn航速下，對一艘70余米長的船，8 s時間的運動段長度一般在1/3船長左右。本算例中，III艙與VII艙之間激勵源的空間距離約為0.55倍的船長，船體聲輻射對應(yīng)的聲源特征長度(指對輻射噪聲起主要貢獻的船體濕表面的跨度，與船長、船體不同部位結(jié)構(gòu)強弱、船內(nèi)激勵源分布以及頻率等因素有關(guān))可認為介于0.55～1倍的船長之間。因此，只取一個8 s時間對應(yīng)的空間跨距不能覆蓋到聲源特征長度，該時間段內(nèi)的聲壓信號不能準確反映整船的輻射噪聲特征。28～36 s、35～43 s和39～47 s 3個時間段的噪聲頻率分布存在差異，如僅取其中的一段，因采樣時段較短，將漏掉有的頻率上的噪聲級高峰，不利于掌握該船的實際輻射噪聲狀態(tài)。將這3個采樣時段對應(yīng)的觀察點空間位置疊加在一起，能覆蓋到約0.8倍的船長，用它評定船舶噪聲級時，有望給出一個在頻譜上能較全面反映整船特征的結(jié)果。因此，可用如下兩種方法改進采樣長度效果：①擴展聲壓信號的采樣時間段長度，對應(yīng)的空間長度最好能接近聲源的特征長度(如取15 s采樣長度，對應(yīng)2/3船長)；②在實船測試中選取多個聲壓均方根值較大的時間段(對應(yīng)不同的空間方位)，將各時間段換算出的聲壓譜進行能量平均后再換算聲源級。

首先嘗試第①種方法。將采樣的聲壓信號長度擴大到15 s，采用第2節(jié)中的方法計算不同15 s長度時間段內(nèi)的聲壓均方根值，以確定具體選取的時間段。根據(jù)圖8，選取其中聲壓均方根值較大的3個時間段，分別是25～40 s、31～46 s和37～52 s，換算成聲源級，結(jié)果如圖9所示。可見：3個15 s時間段信號換算出的聲源級仍存在一定差異；其中C峰值處“時間段25～40 s”和“時間段37～52 s”對應(yīng)的聲源級差異達7.3～7.9 dB；另一方面，由于截取時間的加長，各段的重合部分也增加，圖中3個時間段對應(yīng)的聲源級曲線其吻合度較圖7中的為好；“時間段31～46 s”聲源級曲線在A、B、C3處都能相對較好地體現(xiàn)峰值特征，這一時間段對應(yīng)的空間位置靠近船體中部，相對能較好的覆蓋到船體的主要聲輻射面。圖7中的3個時間段對應(yīng)的聲源級曲線，沒有一個能較完整的反映A、B、C3處的峰值特征；這是因為對該3處峰值起主要貢獻的激勵源和輻射面在艇體的不同部位，而8 s時間段對應(yīng)的觀察點空間長度，無法全面有效地覆蓋到主要的激勵源和輻射面。將采樣信號長度增大為15 s后，觀察點對應(yīng)的空間跨度已可有效地覆蓋到主要的激勵源和輻射面。因此，從反映主要峰值特征而言，截取31～46 s時間段信號換算聲源級是較合適的。

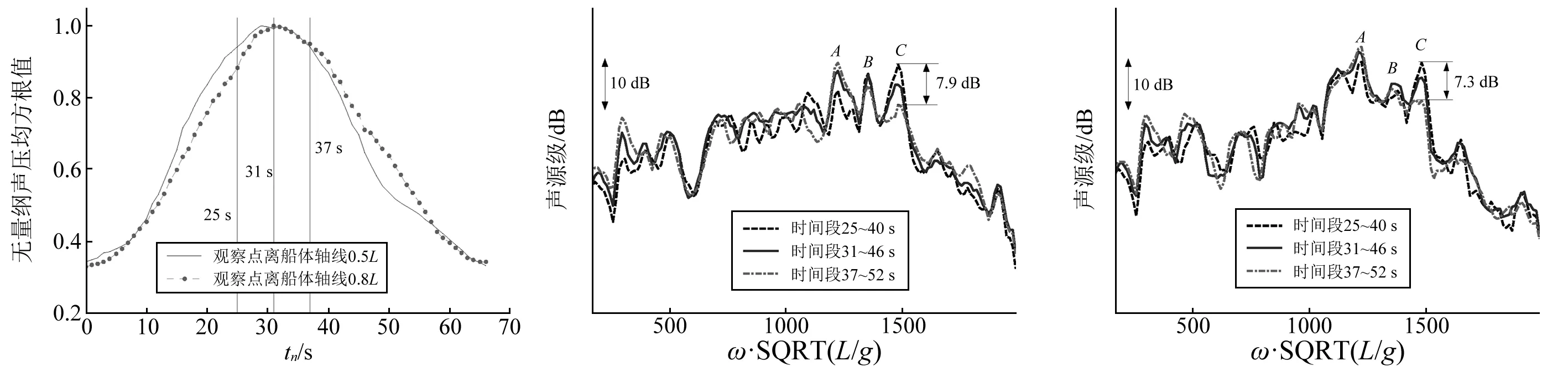
圖8 兩個觀察點在不同15 s時間 (a)離船體軸線距離為0.5L的 (b)離船體軸線距離為0.8L的 段內(nèi)的聲壓均方根曲線 觀察點換算出的聲源級 觀察點換算出的聲源級Fig. 8 Sound pressure rms values of 15 s time 圖9 不同15 s時間段換算出的聲源級結(jié)果 intervals at two observation points Fig. 9 Sound source level transformed from various 15 s time intervals

再嘗試第②種方法。28～36 s、35～43 s和39～47 s 3個8 s時間段疊加覆蓋的空間位置與31～46 s這一15 s時間段覆蓋的空間位置接近。因此，將該3個8 s時間段平均換算出的聲源級與31～46 s時間段換算出的聲源級進行比對，如圖10所示。可見：兩組聲源級曲線幾乎完全重合。從理論基礎(chǔ)和時頻轉(zhuǎn)化的具體算法而言，擴大時間段換算聲源級與多個不同時間段平均換算聲源級具有相同的機理，可以說兩者是等效的。

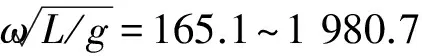
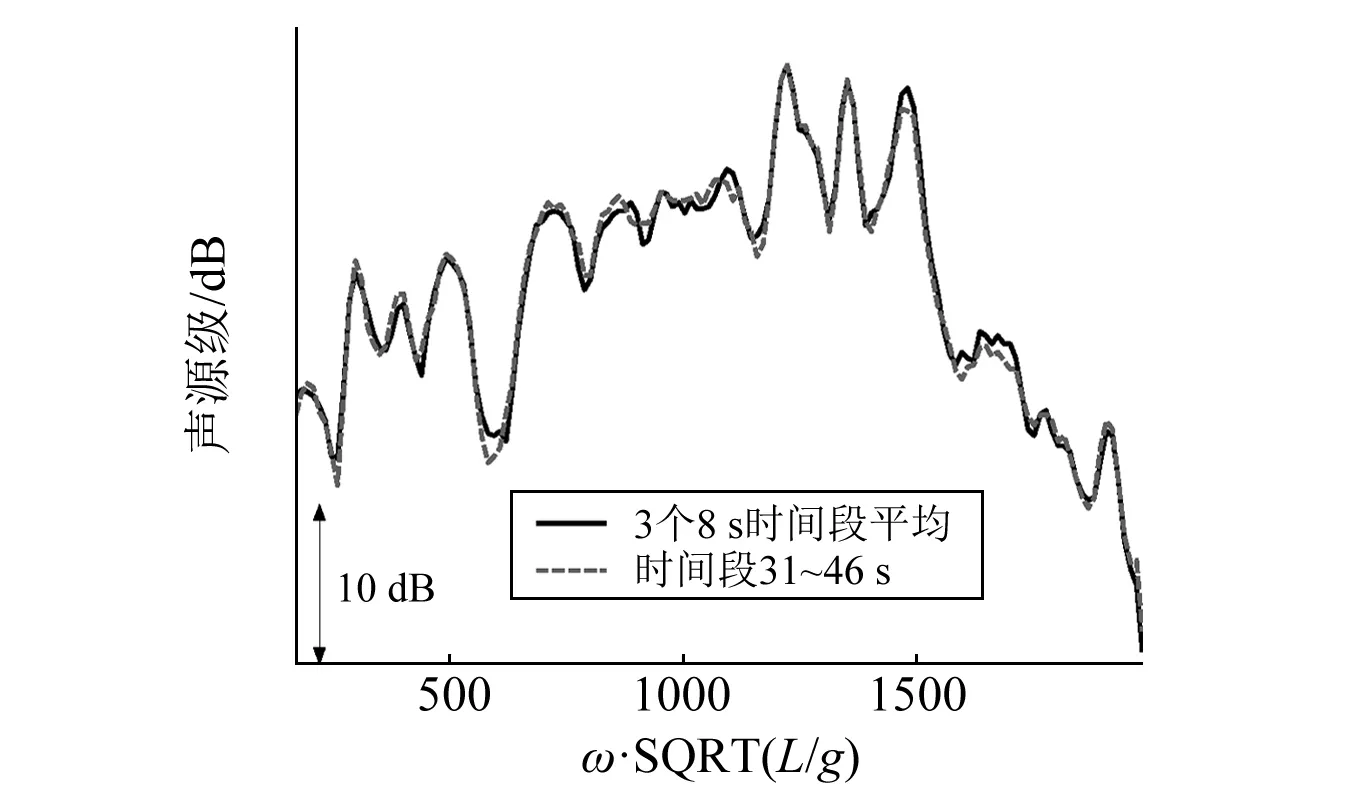
(a)觀察點離船體軸線距離為0.5L

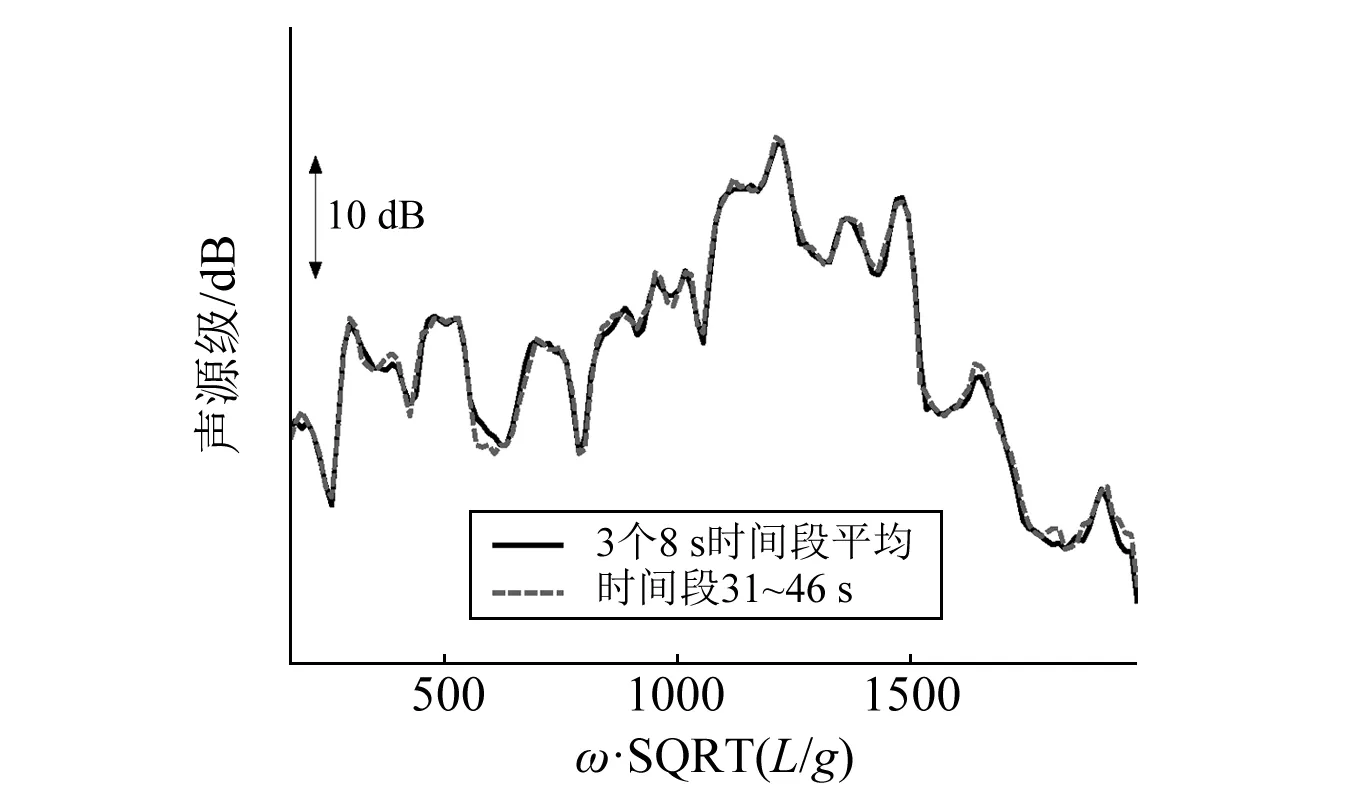
(b)觀察點離船體軸線距離為0.8L圖10 3個8 s時間段平均與15 s時間段換算出的聲源級結(jié)果比對Fig. 10 Sound source levels: three 8 s time intervals averaging vs 15 s time interval

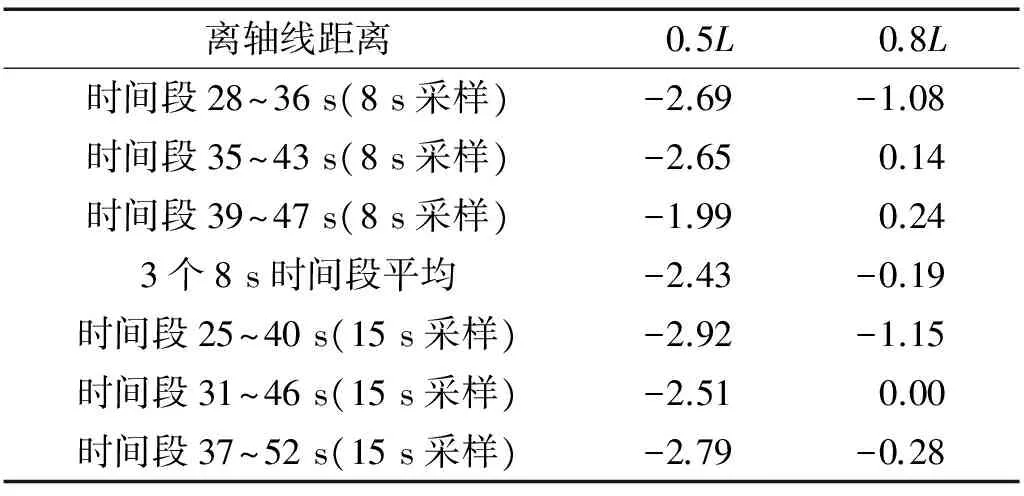
表2 截取不同時間段聲壓信號計算出的相對總聲源級結(jié)果

5 結(jié) 論

本文基于由一個7個艙室組成的實尺度單層殼船體聲彈性計算模型，利用Pekeris水聲波導(dǎo)環(huán)境中的船舶三維聲彈性軟件模塊，模擬實船測試狀態(tài)，計算分析了在3個典型機械激勵力譜作用下，選取觀察點不同采樣時段聲壓信號對船舶聲源級評定影響的部分規(guī)律，給出如下可為實船噪聲級評定測試服務(wù)的建議：

淺水環(huán)境下，在船體舷側(cè)水平方向單點測試聲壓，選取其中最強的時間段信號換算聲源級，該方法在工程上具有較強的可操作性。但也會帶來一些問題，如選取較固定的8 s時間段(觀察點相對移動空間位置較固定)，其覆蓋的范圍只有約1/3船長，而船內(nèi)主要激勵源的分布長度或者船體主要聲輻射面的長度很可能超過這個距離，給出的噪聲級頻譜可能會漏掉實際存在的較顯著的峰值特征，個別峰值相差能達到8 dB。通過本文研究，建議實船測試時采用聲壓信號最強的15 s時間段(或者是觀察點相對運動長度達到2/3船長左右)來換算聲源級，或者是采用多個聲壓較強的不同8 s時間段(對應(yīng)觀察點相對船體的不同空間部位)平均換算聲源級；具體試驗時，可以通過左右舷分別測試、多個有效航次平均的方法，提高結(jié)果的穩(wěn)定性。

[ 1 ] 劉興章. 美國潛艇水聲試驗場現(xiàn)狀及啟示[J]. 艦船科學(xué)技術(shù), 2011,33(2): 140-143.

LIU Xingzhang. Development prospect and revelation of submarine underwater noise test ground of US navy [J]. Ship Science and Technology, 2011,33(2): 140-143.

[ 2 ] 劉興章, 陳濤. 挪威海格納斯?jié)撏曉囼瀳鰷y量設(shè)施分析[J]. 噪聲與振動控制, 2011,31(5): 161-164.

LIU Xingzhang, CHEN Tao. Analysis of facilities of Norwegian acoustic testing field in Heggernes[J]. Noise and Vibration Control, 2011,31(5): 161-164.

[ 3 ] 鄒春平,陳端石，華宏星. 船舶水下輻射噪聲特性研究[J]. 船舶力學(xué), 2004，8(1): 113-124.

ZOU Chunping, CHEN Duanshi, HUA Hongxing. Study on characteristics of ship underwater radiation noise[J]. Journal of Ship Mechanics, 2004, 8(1): 113-124.

[ 4 ] 祁立波. 槳-軸-艇體耦合振動聲輻射的三維聲彈性分析方法[D].無錫：中國船舶科學(xué)研究中心, 2015.

[ 5 ] LI W L, WU T W, SEYBERT A F. A half-space boundary element method for acoustic problems with a reflecting plane of arbitrary impedance[J]. Journal of Sound and Vibration, 1994,171(2): 173-184.

[ 6 ] 鄒元杰, 趙德有. 結(jié)構(gòu)在淺水中的振動和聲輻射特性研究[J]. 振動工程學(xué)報, 2004,17(3): 269-274.

ZOU Yuanjie, ZHAO Deyou. A vibro-acoustic study on structures in shallow water[J]. Journal of Vibration Engineering, 2004，17(3): 269-274.

[ 7 ] ZOU M S, WU Y S, LIU Y M,et al. A three-dimensional hydroelasticity theory for ship structures in acoustic field of shallow sea[J]. Journal of Hydrodynamics, 2013,25(6): 929-937.

[ 8 ] 鄒明松. 船舶三維聲彈性理論[D].無錫：中國船舶科學(xué)研究中心, 2014.

[ 9 ] 鄒明松, 吳有生, 孫建剛, 等. 基于船舶三維聲彈性理論的計算技術(shù)[J]. 聲學(xué)技術(shù), 2016，35(6): 112-115.

ZOU Mingsong, WU Yousheng, SUN Jiangang,et al. Computational techniques based on the three-dimensional sono-elasticity of ships[J]. Technical Acoustic, 2016,35(6): 112-115.