液壓式動力反共振隔振器帶寬分析

肖 晗， 董興建， 彭志科， 孟 光

(上海交通大學 機械系統與振動國家重點實驗室振動與沖擊、噪聲研究所，上海 200240)

動力反共振隔振是一種新型隔振技術，其突出優勢是在不降低系統靜剛度的條件下實現線譜振動的隔離，并且在反共振頻率上具有非常高的隔振效率，通?？蛇_95%以上[1]。這一優勢使得動力反共振隔振成功地解決了直升機主減-機身的低頻隔振問題：既隔離了主減到機身的線譜振動，又不降低主減與機身之間的靜剛度。動力反共振隔振的慣性放大機制主要由機械杠桿或液壓杠桿來實現。Flannelly等[2-5]給出了不同形式的機械式動力反共振隔振器，并成功應用在NH90、BO105等輕中型直升機中。1980年，Braun[6-7]提出了一種液壓式動力反共振隔振器，并在EC135等直升機上得到應用，顯示出良好的隔振性能。相比機械式動力反共振隔振器，液壓式動力反共振隔振器具有結構對稱，安裝方便，低阻尼和低噪聲等優點[8]，應用前景廣闊。

動力反共振隔振器具有較強的頻率選擇性，限制了其應用的范圍。為了在較寬的頻帶內實現動力反共振隔振，有必要分析動力反共振隔振器的帶寬并對其進行優化設計，為動力反共振隔振器的寬頻帶設計提供理論指導[9-10]。在某種意義上，動力反共振隔振器可以看作一種陷波濾波器，其帶寬定義為隔振器在給定傳遞率下實現有效振動衰減的頻率范圍[11-12]。對于液壓式動力反共振隔振的帶寬設計，目前鮮見文獻報導。建立了兩種液壓式動力反共振隔振器模型，討論了隔振帶寬與慣性元件質量、放大比等參數的關系；給出了一種雙層隔振器設計思路，以實現寬頻帶反共振隔振。

1 液壓式動力反共振隔振器帶寬

液壓式動力反共振隔振器由彈簧、大小波紋管和慣性質量塊構成。當給基座施加激勵時，金屬波紋管內的流體會發生往復運動，在特定激勵頻率下，由流體運動產生的動壓力與彈簧提供的彈性力相平衡，阻斷了振動向隔振對象的傳遞，從而使得隔振對象位移為零。這一頻率即為反共振頻率。

相比傳統的動力吸振器，反共振隔振器通過引入慣性放大機構，能以較小的附加質量實現較好的隔振效果。機械式動力反共振隔振器通過機械式杠桿來實現慣性放大，液壓式動力反共振隔振器通過兩個不同截面積的金屬波紋管來實現慣性放大。根據波紋管的安裝形式，提出了兩種類型的液壓式動力反共振隔振器，Ⅰ型和Ⅱ型，分別討論了它們的隔振帶寬。

1.1 Ⅰ型液壓式反共振動力隔振器

圖1為Ⅰ型動力反共振隔振器的原理圖，隔振器置于基座和隔振對象之間，其中Ap為大波紋管有效橫截面積；As為小波紋管有效橫截面積；k為彈簧剛度；x為隔振對象位移；y為基座位移；z為慣性質量位移；m為隔振對象質量；mis為慣性元件質量，定義放大比為α=Ap/As且α>1，假設水不可壓縮，流體體積不變。根據流體連續性方程，得到位移關系

(1)

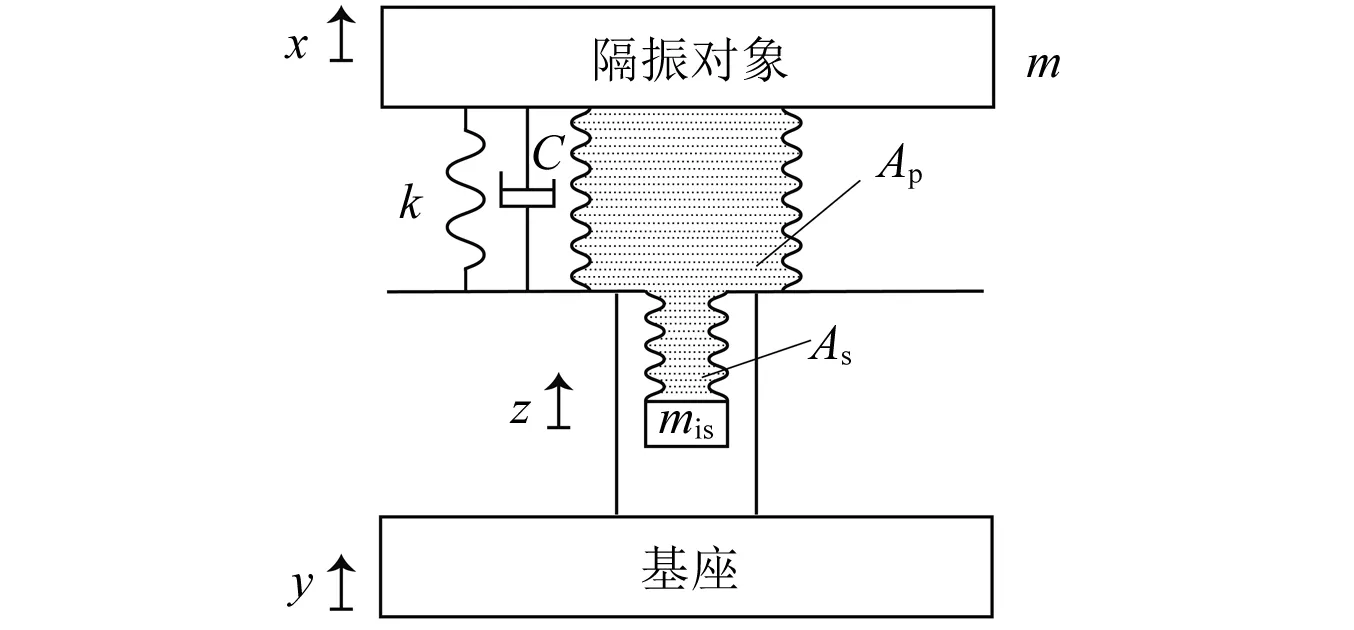
圖1 Ⅰ型液壓式動力反共振隔振器Fig.1 Type Ⅰ hydraulic anti-resonant vibration isolator

動力學方程可以寫為

(2)

(3)

對基座施加簡諧激勵， 記x=Xeiωt,y=Yeiωt， 根據式(2)和式(3)可以得到系統的極點

(4)

以及系統的零點

(5)

系統的位移傳遞率為

(6)

更進一步，可以得到

(7)

僅要求系統在反共振點具有隔振特性是不夠的，一般情況下，我們更關心隔振器在多大的頻率范圍內具有良好的隔振性能。對基座施加位移激勵，如果允許的最大位移傳遞率為T0， 那么將位移傳遞率絕對值小于T0的頻率范圍稱為隔振帶寬(Bandwidth)。將隔振帶寬的中心頻率定義為系統零點ωz， 記N=ω0/ωz。

在給定最大位移傳遞率T0的情況下， 對式(6)取絕對值并令其等于T0， 可以得到兩個解，即系統的下截止頻率ωs1和上截止頻率ωs2(ωs1<ωs2)。進行歸一化處理，定義隔振帶寬為

(8)

為了便于求解截止頻率，引入以下關系

(9)

進一步，確定式(8)中的l和m即可確定截止頻率。

由式(5)可得

(10)

由式(4)、式(5) 和式(10)得到零極點的關系

(11)

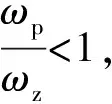
將式(10)代入式(6)并令之為-T0，可以得到

(12)

同樣地，將式(10)代入式(6)并令之為T0，可以得到

(13)

由式(8)和式(9)有

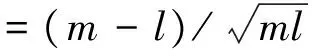
(14)

將式(12)、式(13)代入式(14)，即可得到隔振帶寬的表達式

(15)

對于低頻隔振，那么N>1。最大位移傳遞率與隔振要求有關，一般應滿足T0?1。但是，如果T0過小，會使得隔振頻帶過窄，這樣就難以滿足實際的隔振要求，在實際的應用中過低的最大位移傳遞率并沒有必要。根據式(15)，可以計算出一定質量比和頻率比條件下的隔振帶寬。

記f=ω/ω0， 給定N=2，μ=0.1， 作出傳遞率絕對值隨f的變化圖。圖2為Ⅰ型隔振器位移傳遞率絕對值圖。

圖2 Ⅰ型隔振器位移傳遞率絕對值圖Fig.2 Transmissibility plots showing the bandwidth of a type Ⅰ isolator

從圖2中可見，Ⅰ型液壓式反共振隔振器在反共振點周圍一定頻率范圍內形成隔振帶寬，如果位移傳遞率為0.1，則隔振帶寬為0.042 2。

1.2 Ⅱ型液壓式反共振動力隔振器

圖3是Ⅱ型液壓式反共振隔振器形式，它與Ⅰ型隔振器原理相同，但慣性質量和和隔振對象具有不同的相對運動方向，忽略阻尼，其動力學方程為

(16)

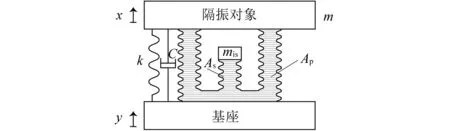
圖3 Ⅱ型液壓式動力反共振隔振器Fig.3 Type Ⅱ hydraulic anti-resonant vibration isolator

系統的位移傳遞率為

(17)

根據式(16)可以得到Ⅱ型隔振器零極點位置關系

(18)

從式(17)可以看出，Ⅱ型液壓式反共振隔振器的零極點大小關系并不明確，選取不同的放大比α，零極點的大小關系將會發生變化。

采用同樣的方法，可以得到Ⅱ型隔振器隔振帶寬表達式

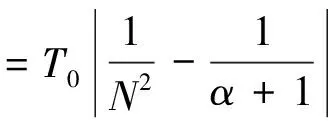
(19)

同樣，在N=2，μ=0.1時， 作位移傳遞率絕對值圖。圖4為Ⅱ型隔振器位移傳遞率絕對值曲線。

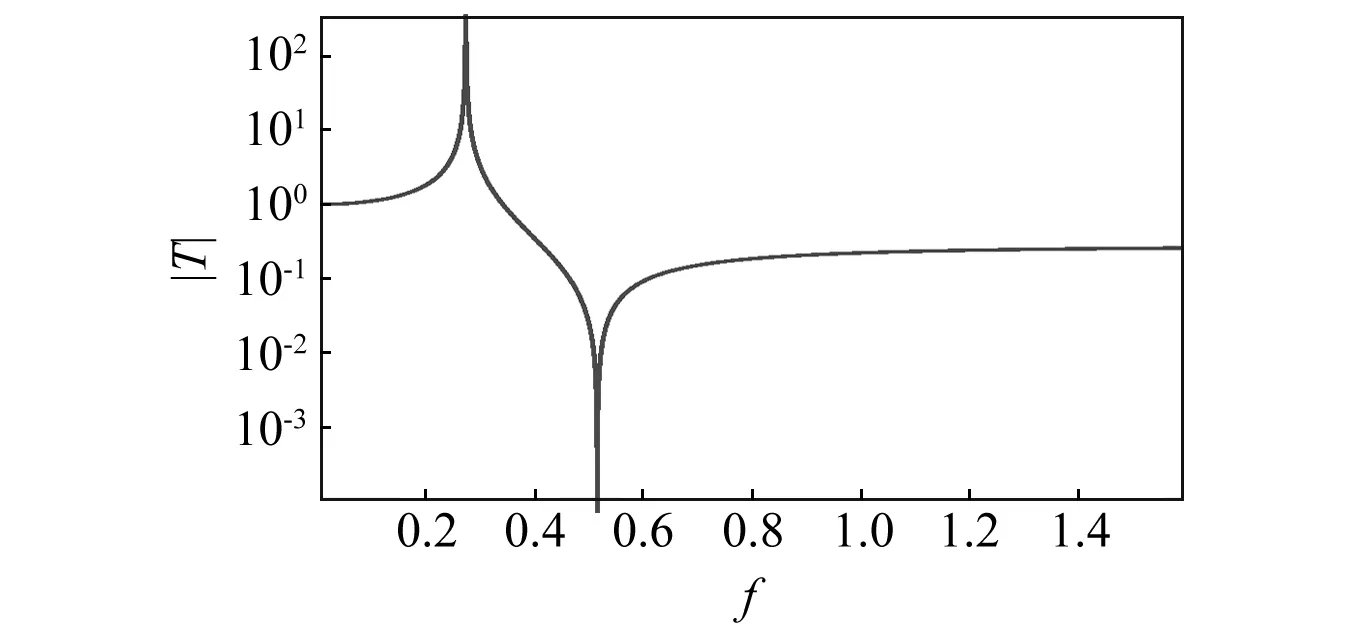
圖4 Ⅱ型隔振器位移傳遞率絕對值圖Fig.4 Transmissibility plots showing the bandwidth of a type Ⅱ isolator

圖2和圖4表明，Ⅰ型和Ⅱ型隔振器具有相同的隔振原理，如果位移傳遞率為0.1，Ⅱ型隔振器的隔振帶寬為0.010 2，比Ⅰ型隔振器帶寬要小。

2 隔振器帶寬分析

下面對Ⅰ型和Ⅱ型液壓式反共振隔振器帶寬進行比較。

圖5是T0=0.05時，帶寬隨放大比α以及N的變化關系圖?？梢钥闯?，對Ⅰ型和Ⅱ型液壓式動力反共振隔振器，在α和N取一定值的時候，都會出現隔振帶寬最小的情況。從圖中還可以看出，隔振帶寬可以無限大，但此時需要很小的α或者N，在工程設計中沒有意義。

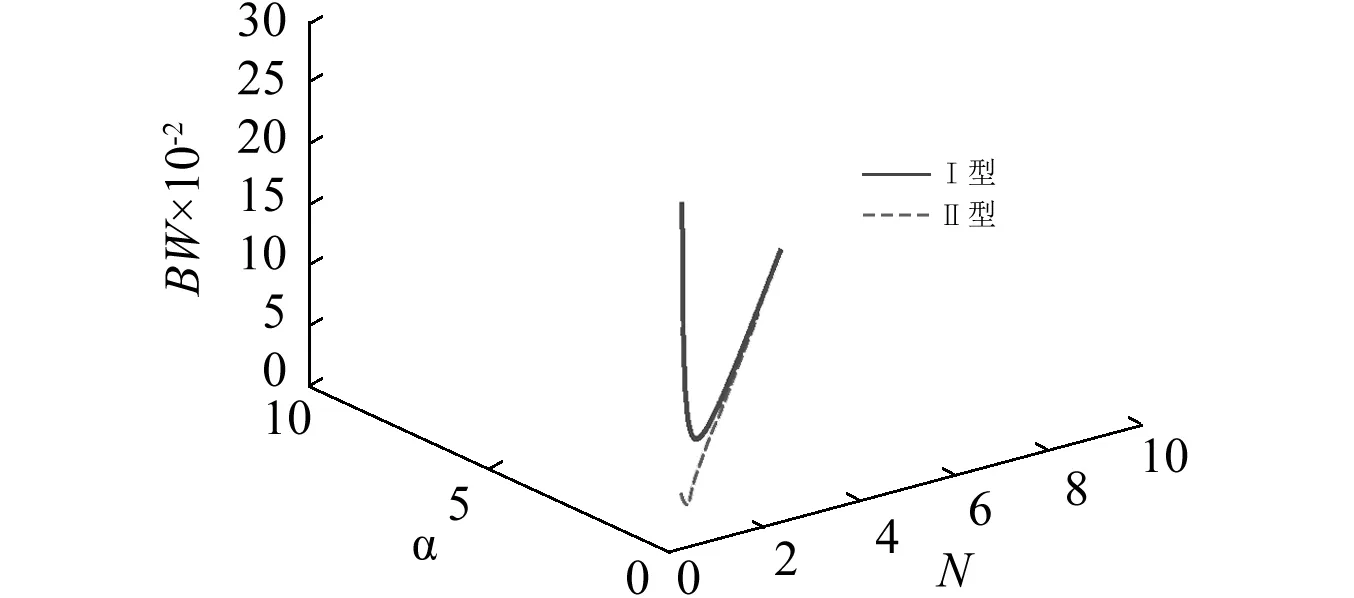
圖5 帶寬隨α，N變化圖Fig.5 Bandwidth versus α and N comparisons

取位移傳遞率T0=0.05， 圖6為N=2時隔振帶寬與放大比α的關系， 圖7是隔振帶寬與N的關系。

從圖6可以看出，在固定N為2 的時候，Ⅰ型隔振器比Ⅱ型隔振器具有更大的帶寬。Ⅰ型隔振器的帶寬隨著放大比增大而降低，Ⅱ型隔振器不同，在放大比為3的時候帶寬為0，也即沒有隔振效果，接著隨著放大比增加帶寬增加。理論上，取較小的放大比可以得到較大的帶寬，但由式(10)可以看出，放大比和質量比呈負相關關系，如果α→1， 則μ→∞。 這意味著，如果采取很小的放大比，則需要非常大的慣性質量，這在工程設計中也是沒有意義的。

圖6 帶寬隨放大比α變化圖Fig.6 Bandwidth versus α comparisons

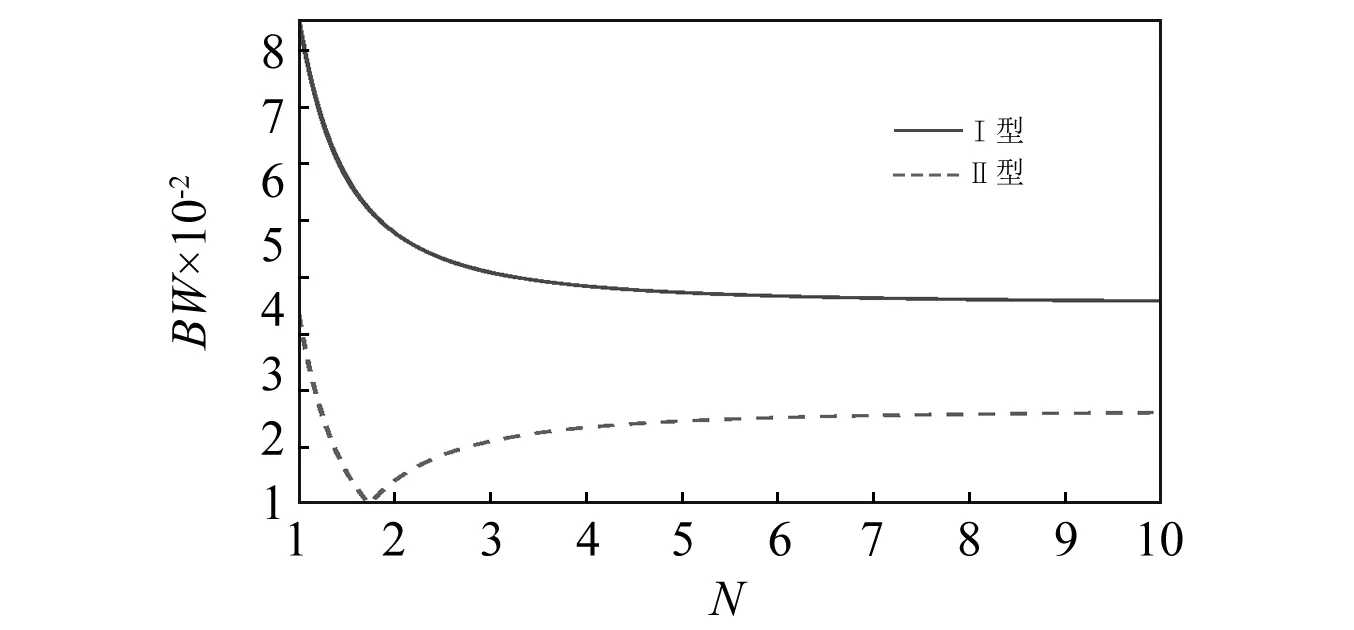
圖7 帶寬隨頻率比N變化圖Fig.7 Bandwidth versus N comparisons

同樣，從圖7可以看出，在固定放大比α為2的時候，Ⅰ型隔振器帶寬隨著頻率比增大而減小，而Ⅱ型隔振器仍會出現帶寬為0的情況。類似地，取較小的頻率比可以得到較大的帶寬，但是由于低頻應用的條件，希望反共振頻率要適當小于系統無阻尼自然頻率，這時可根據實際需要確定相應的頻率比。

對于不同的放大比和頻率比，Ⅰ型隔振器的隔振帶寬總是大于Ⅱ型隔振器的隔振帶寬。在單自由度隔振系統中，采用Ⅰ型隔振器比Ⅱ型隔振器具有更好的效果。

3 雙層液壓式反共振隔振器設計

3.1 動力學模型

前面已經討論了兩種單自由度液壓式反共振隔振器，可以看到，隔振器在反共振頻率周圍形成了隔振帶寬。如果再引入其它的反共振點，并且使這些反共振點接近，則可以進一步擴大帶寬。理論上，可以引入盡可能多的反共振點，考慮到實際情況，只討論2自由度的情況。

圖8為一種雙層液壓式反共振隔振器的設計。它分為上下兩層，下層為Ⅱ型液壓式反共振隔振器，上層為Ⅰ型液壓式反共振隔振器。記Ⅰ、Ⅱ型隔振器零點分別為ωz Ⅰ和ωz Ⅱ，極點分別為ωp Ⅰ和ωp Ⅱ。為了得到較大的帶寬，可以使Ⅱ型隔振器滿足ωz Ⅱ<ωp Ⅱ， 而Ⅰ型隔振器始終滿足ωp Ⅰ<ωz Ⅰ，從而實現

ωp Ⅰ<ωz Ⅰ<ωz Ⅱ<ωp Ⅱ

(20)

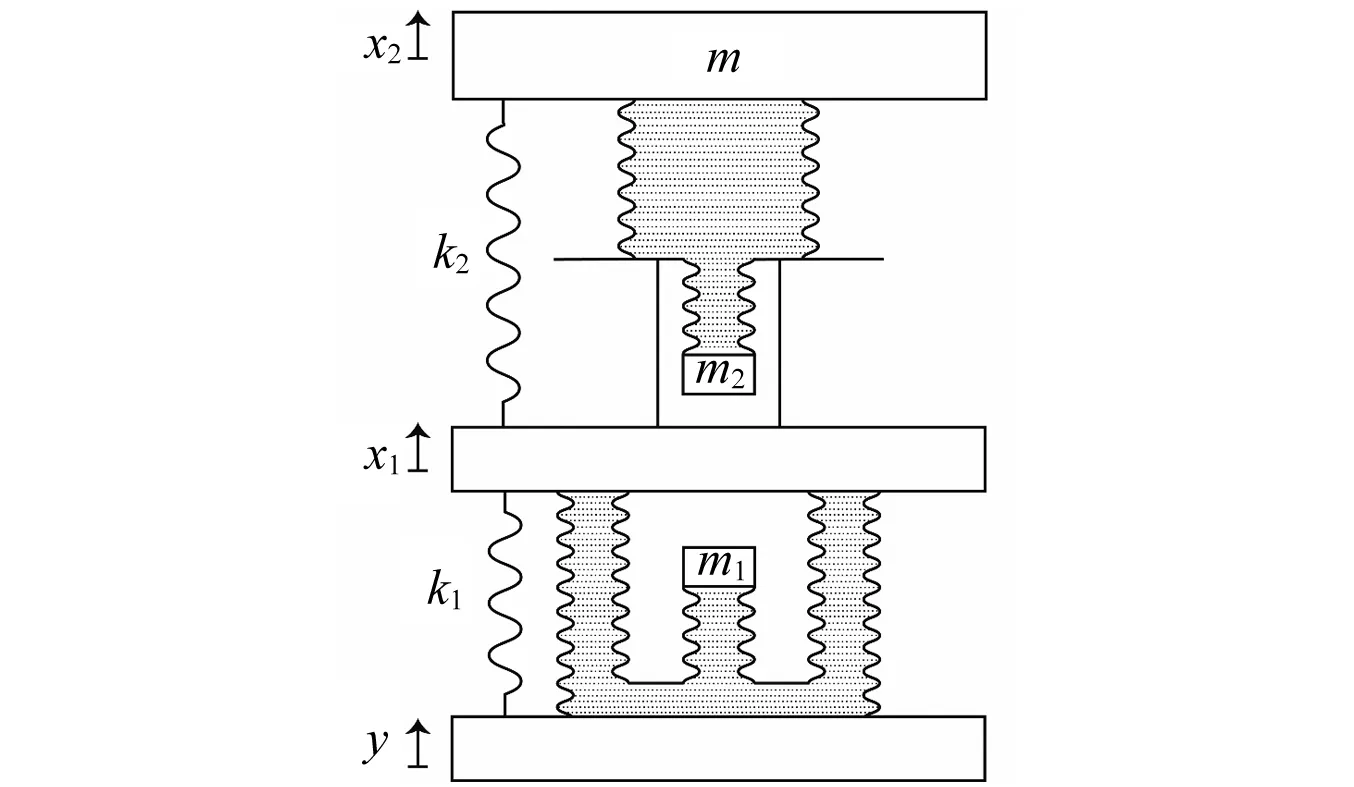
圖8 雙層液壓式反共振隔振器Fig.8 2-dof hydraulic anti-resonant vibration isolator

該系統的動力學方程為

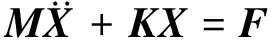
(21)

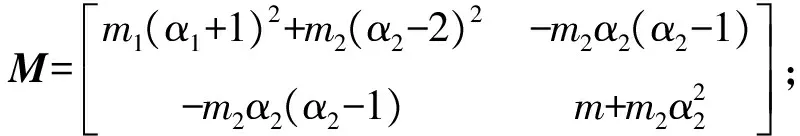
系統的位移傳遞率為

(22)

其中，

進一步，可以將式(22)改寫成

(23)

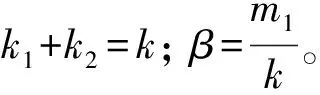
從式(21)可以看出，雙層隔振器的零點表達式與單層一樣，但極點形式發生了變化。記系統零極點為ωz1，ωz2，ωp1，ωp1。則為

ωz1=ωz Ⅰ,ωz2=ωz Ⅱ

(24)

記較小的極點為ωp1， 下面比較ωp1和ωp Ⅰ的大小。 考慮ωp Ⅰ時，可將第一層隔振器和基座看作一個整體，隔振器工作時，系統彈簧處于同時拉伸或壓縮的狀態，此時作用在上層上的力減小，從而有ωp1<ωp Ⅰ。

另一方面，比較ωp2和ωp Ⅱ的大小。 考慮ωp Ⅱ時，可將上層隔振器和隔振對象看做一個整體，隔振器工作時，上下層彈簧狀態不同，這將導致作用在下層上的力增加，因而有ωp Ⅱ<ωp2。

由以上討論可以得到雙層液壓式反共振隔振器的零極點位置關系

ωp1<ωz1<ωz2<ωp2

(25)

3.2 隔振帶寬優化設計

確定系統允許的最大傳達率T0后， 由T(ω)=-T0可以得到隔振帶寬的截止頻率ωs1和ωs2。由于在系統帶寬范圍內存在兩個零點，因此在帶寬內存在使得傳遞率絕對值取最大值的頻率，記該頻率為ωm。優化目標函數為

約束條件

k1,k2≥k,m1,m2≥0,α1,α2≥1

在優化過程中，有6個變量，m1，m2，k1，k2，α1，α2。將m2，k2，α1，α2稱為過程變量，剩下的m1，k1稱為決策變量。根據h2和h3可以解得m2和k2。通過h1和h4確定α1和α2。 給定μ，N,T0,m和k均取為1。根據設定的初始條件，采用遺傳算法進行優化，得到m1和k1，從而得到4個過程變量，結果見表1和表2。

表1 μ=0.1, N=2, T0=0.05時，優化結果

從圖9可以看出，雙層隔振器有兩個反共振點，給定最大位移傳遞率時，利用兩個反共振點附近的頻率范圍得到隔振帶寬。雙層隔振器相比于Ⅰ型隔振器具有更大的帶寬，將近2.26倍。圖9中的局部最大值即為給定的最大位移傳遞率。

表2 μ=0.5, N=2, T0=0.05時，優化結果

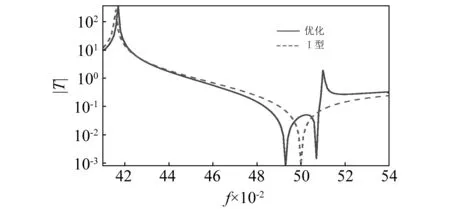
圖9 優化結果與Ⅱ型隔振器比Fig.9 Bandwidth comparison of the 2-dof optimum design and a type Ⅱ isolator

圖9和圖10表明，較大的質量比可以得到更大的帶寬。然而，提高質量比會增加系統負擔，實際設計過程中應該綜合來考慮。

圖10 優化結果與Ⅱ型隔振器比較Fig.10 Bandwidth comparison of the 2-dof optimum design and a type Ⅱ isolator

4 結 論

建立了液壓式動力反共振隔振器的帶寬表達式， 帶寬隨α的增加而減小， 隨N的減小而增加。選擇盡可能小的放大比可以得到較大的帶寬，但此時隔振系統所需的慣性質量過大，這在實際設計中是要避免的。同時，N的減小與通常低頻隔振的要求相違背，因此，在液壓式動力反共振隔振器的帶寬設計中，要綜合考慮α和N對帶寬的影響，并避開使得帶寬最小的α和N的取值。最后，提出了一種雙層液壓式動力反共振隔振器，優化分析表明，在給定最大位移傳遞率時，通過選取隔振器的參數，可以獲得最大的隔振帶寬。與Ⅰ型隔振器相比，雙層隔振器比單層隔振器具有更大的隔振帶寬。

[ 1 ] 顧仲權. 動力反共振隔振[J]. 噪聲與振動控制, 1989(6): 36-40.

GU Zhongquan. Dynamic anti resonance vibration isolation [J]. Noise and Vibration Control, 1989(6): 36-40.

[ 2 ] FLANNELLY W G. Dynamic antiresonant vibration isolator: U.S. 3,322,379 [P]. 1967-05-26.

[ 3 ] RITA A D, MCGARVEY J H, JONES R. Helicopter rotor isolation evaluation utilizing the dynamic antiresonant vibration isolator [J]. Journal of the American Helicopter Society, 1976, 23(1): 22.

[ 4 ] DESJARDINS R A. Vibration isolation system: U.S. 4,140,028 [P]. 1979.

[ 5 ] DESJARDINS R A, HOOPER W E. Antiresonant rotor isolation for vibration reduction [J]. Journal of the American Helicopter Society, 1980, 25(3): 46-55.

[ 6 ] BRAUN D. Development of antiresonance force isolators for helicopter vibration reduction [J]. Journal of the American Helicopter Society, 1982, 27(4): 37-44.

[ 7 ] BRAUN D. Vibration isolator particularly of the antiresonance force type: U.S. 4,781,363 [P]. 1988-11-01.

[ 8 ] 孫忠池. 反共振理論在動力吸振器設計中的應用[J]. 應用力學學報, 1993, 10(4): 97-103.

SUN Zhongchi. The application of anti-resonance theory in design of vibration absorbers [J]. Chinese Journal of Applied Mechanics, 1993, 10(4): 97-103.

[ 9 ] YILMAZ C, KIKUCHI N. Analysis and design of passive band-stop filter-type vibration isolators for low-frequency applications [J]. Journal of Sound and Vibration, 2005, 291(3): 1004-1028.

[10] YILMAZ C, KIKUCHI N. Analysis and design of passive low-pass filter-type vibration isolators considering stiffness and mass limitations [J]. Journal of Sound and Vibration, 2006, 293(1): 171-195.

[11] 劉春嶸,冀建飛,徐道臨. 反共振流體浮筏的隔振特性研究[J]. 力學與實踐, 2012, 34(2): 49-53.

LIU Chunrong, JI Jianfei, XU Daolin. Vibration isolation of fluid-type anti-resonance floating raft system [J]. Mechanics in Engineering, 2012, 34(2): 49-53.

[12] HUANG Xiuchang, JIANG Aihua, ZHANG Zhiyi, et al. Design and optimization of periodic structure mechanical filter in suppression of foundation resonances [J]. Journal of Sound and Vibration, 2011, 330(20): 4689-4712.