基于動態貝葉斯網絡的民用機場空襲毀傷評估模型

李其然,史玉彬,陳志華,鄭 純,孫曉暉

(1.南京理工大學 瞬態物理國家重點實驗室,江蘇 南京 210094;2.陸軍武器裝備體系研究國防科技重點實驗室,北京100012;3.南京理工大學 機械工程學院,江蘇 南京 210094)

現代戰爭中,制空權是相當重要的一個環節,戰局由地面轉向空中,并且由空襲主導[1]。而機場目標更是爭奪的重點,也是各種戰斗中最優先打擊的目標之一。飛機從出動到完成任務返回機場,都依賴于機場的各種設施[2]。軍用機場的重要性不言而喻,民用機場由于其設備通用性強,也可作為軍用機場的戰略替代品。所以無論是進攻還是防御都應對民用機場進行毀傷分析。

目標毀傷效果評估(BDA)[3]是對敵方火力打擊后目標的毀傷效果進行綜合評估,作戰決策人員據此分析戰后數據及圖像,可以判斷是否需要二次打擊,從而對戰局產生影響。BDA在如今信息化作戰體系中是不可或缺的關鍵環節。傳統決策中,對于BDA處理方法有多目標決策分析(MODA)、神經網絡(ANN)方法、模糊綜合評價、決策樹等[4-6],而目前國內外應用范圍廣、穩定性高的評估方法為貝葉斯網絡法。

動態貝葉斯網絡基于貝葉斯網絡的架構,綜合考慮時間對變量的影響,實現信息在時間上的積累與互補,因此,它不僅繼承了貝葉斯網絡模擬概率推理結果的主架構,更能反映出未來目標毀傷等級的變化,同時容錯率增高,能有效解決在毀傷評估中的關鍵問題。

本文基于動態貝葉斯網絡技術,提出了一種對民用機場進行空襲毀傷評估的模型,并通過與模擬實驗結果對比,以及模型精確度與穩定性驗算,驗證了其有效性,可為民用機場設計等提供重要指導。

1 動態貝葉斯網絡

動態貝葉斯網絡的基礎是馬爾科夫模型和靜態貝葉斯網絡,由初始網絡和時間轉移網絡兩部分組成。

將總時間tT分割為j個時間節點(t=1,2,…,j),對于初始時間節點t=1,結點之間的邊以及概率函數、先驗網絡無變化。設X={X1,…,Xn}是動態貝葉斯網絡隨機變量集,Xi[t]表示變量Xi(i=1,2,…,n)在t時間節點對應的隨機變量。對某一節點Xi,先驗網B0代表初始狀態概率分布,轉移網B→代表t時間節點到t+1時間節點的轉移概率PB(Xi[t+1]|Xi[t])。因此,給定一個動態貝葉斯網絡模型,對某一節點Xi在Xi[1],…,Xi[n]上的聯合概率分布[7-8]可表示為

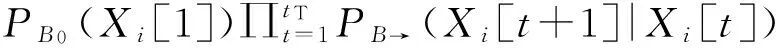
(1)

2 毀傷評估模型的建立

2.1 系統分析

一般民用機場系統運用結構劃法可分為航站樓、跑道和機坪3個子系統。本文考慮戰時的特殊情況,發現航站樓戰略意義不大以及結構劃分各個子系統對總系統的影響嚴重不均衡等問題,新創功能劃分法,將民用機場X0劃分為飛機設施X1、指揮設施X2、后勤設施X33個子系統,各個子系統相互關聯。

細分來看,3項設施有著各自的二級子系統:①飛機場地X1。這部分主要功能是供飛機起飛、著落和停放,二級子系統包括跑道X11、停機坪X12、滑行道X13。②指揮設施X2。指揮飛機起飛、降落及正常飛行,包括指揮中心X21、塔臺X22、雷達系統X23。③后勤設施X3。保障各項運作的供給,包括修理廠X31、裝備庫X32(油庫、彈藥庫)、能源站X33(充氣站、充電站、冷氣站)。

2.2 毀傷效果評估與動態貝葉斯模型

利用戰場探測所得的信息,量化特征參量使其能夠直觀反映目標的毀傷效果,建立毀傷等級評估模型。本文遵循簡化、便于計算的原則,對于一般民用機場,建立如下節點狀態集合。

總系統X0:{輕(L),中(N),重(H)},一級子系統Xi(i=1,2,3):{輕(L),中(N),重(H)}。二級子系統Xij(i,j=1,2,3):{輕(L),中(N),重(H)}。

對任一系統Xp中的狀態(L,N,H),用概率P表示,P取值范圍為(0,1),且

P(Xp=L)+P(Xp=N)+P(Xp=H)=1

最后,在網絡隨時間變化的同時,對相鄰時間片建立狀態轉移概率矩陣,此民用機場毀傷效果評估結構模型建立完成,如圖1所示。圖中,某一時間節點t某一系統Xp毀傷概率為輕的概率表示為P(Xp[t]=L)。

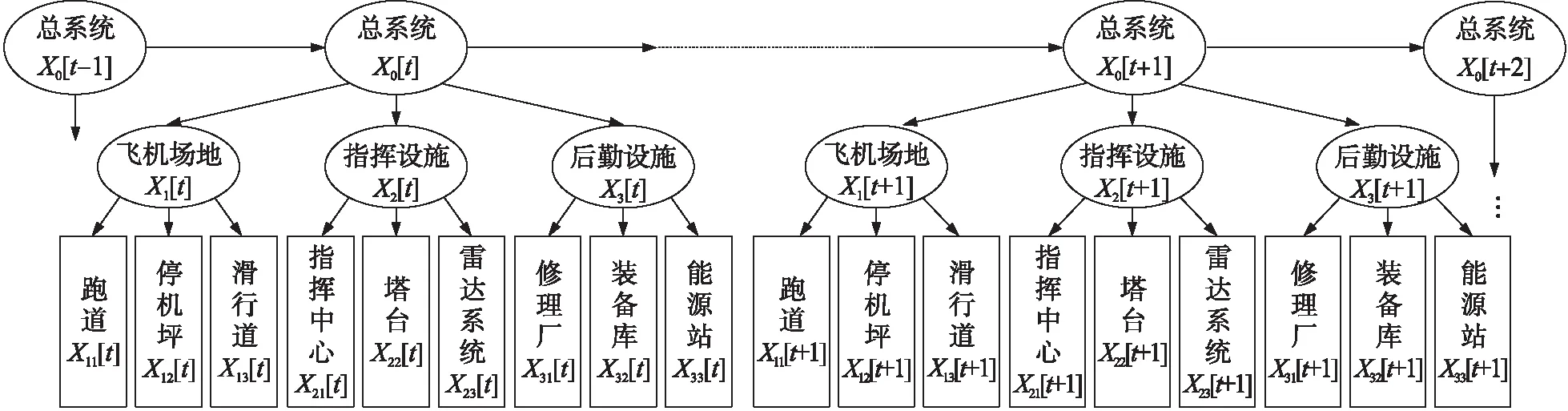
圖1 民用機場動態貝葉斯網絡模型

2.3 模型運行流程

基于動態貝葉斯網絡的毀傷評估步驟如下。

①前期準備。分析某一具體民用機場,確定各個設施對應的具體節點位置,確定模型的物理結構框架。

②模型數學化。結合目標實際情況與專家意見,建立各個父子結點的條件概率分布表與時間片傳遞的狀態轉移表,完成模型的數學公式內核。

③模型處理信息。打擊行動中按照指揮部要求由偵查單位反饋共計m個時間節點的各個三級子系統觀測數據,接入模型輸入層進行處理。

④得出結果反饋。模型將處理的結果反饋指揮部,由指揮部決定是否進行再打擊行動。

整體流程如圖2所示。

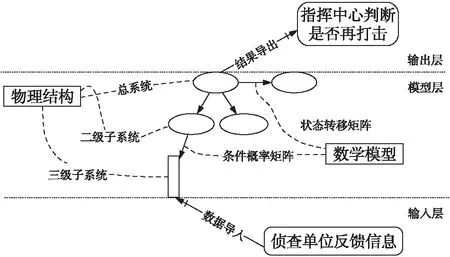
圖2 毀傷評估整體流程圖

3 模型檢驗

模型檢驗分2個方面,包括檢驗模型的有效性和穩定性。

3.1 模型的有效性檢驗

按照前文2.3節的描述,構建基于動態貝葉斯網絡的民用機場毀傷效果評估模型并使用NETICA軟件[9]進行仿真計算。假設目標為某一民用機場,將總時間tT均分為10個時間節點,每個時間節點用t(t=1,2,…,10)表示,通過專家確定網格中每個條件概率分布表。表1為X1與其子節點X11,X12,X13條件概率分布表,表中,PX11,PX12,PX13分別表示跑道毀傷評估,停機坪毀傷評估和滑行道毀傷評估的條件概率,其余的不再贅述。同時確立狀態轉移概率表,如表2所示,表中,w為Pk(X0[t]=S)(S∈{L,N,H}的更新權重。

本文采用蒙特卡洛法建立毀傷過程模擬觀測數據,該方法相較靶場實驗法有著高效簡便、數據貼合實際的特點[10],可以作為現實數據的替代品從而檢驗模型。

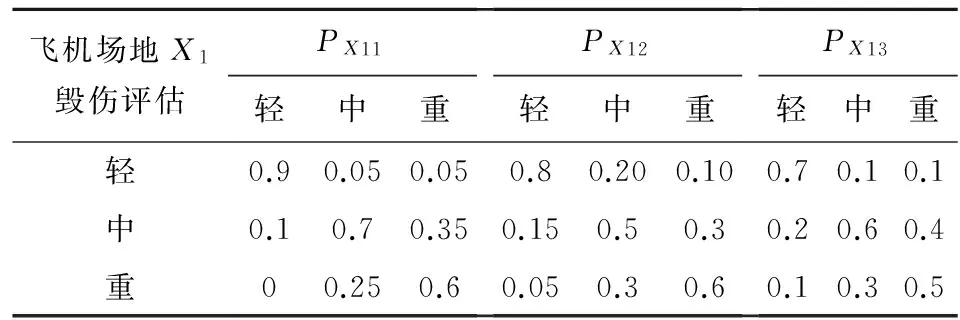
表1 飛機場地X1毀傷評估條件概率表

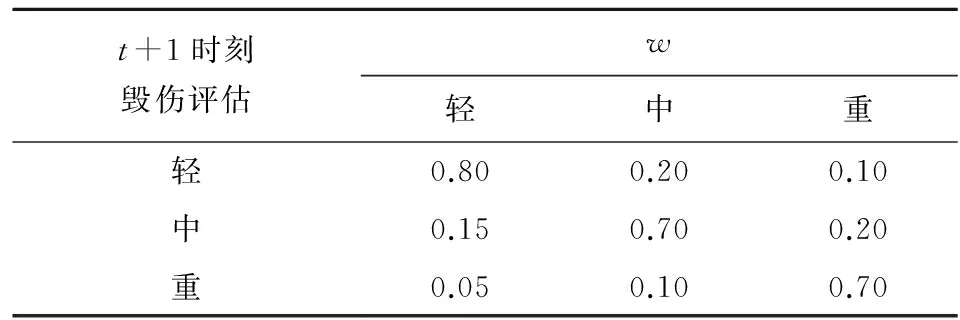
表2 動態貝葉斯網絡狀態轉移概率表

為方便計算做以下假設:在每一時間片對每一個三級子系統投射10發殺爆彈;民用機場模型來源于某民用機場。將蒙特卡洛法模擬的觀測數據代入動態貝葉斯毀傷評估模型,計算得出的結果與模擬實驗結果進行對比,其中選取總系統毀傷評估為輕、中、重的概率:{Pk(X0[t]=S)|t∈(1,10),S∈{L,N,H},k={0,1}},式中:k=0為模擬實驗結果,k=1為本模型結果,做折線圖,如圖3所示。

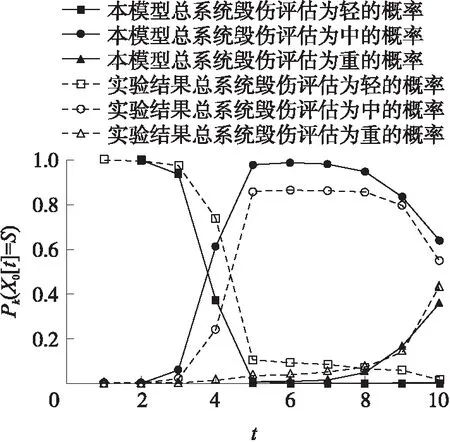
圖3 本文模型與模擬實驗的毀傷評估概率對比圖

同時引入皮爾森相關系數r以量化該模型與模擬實驗結果的數據相關程度(趨于0說明相關度高,趨于1說明相關度低),計算可得本模型總系統毀傷評估概率為輕、中、重的皮爾森系數分別為0.016 82,9.4×10-15,7.1×10-17。選取其均值0.005 61,與文獻[11-12]模型的皮爾森系數均值進行對比,如圖4所示,得出本文模型的皮爾森系數均值較其他兩模型的皮爾森系數降低了50.83%,82.23%,說明了本文模型與實驗結果相關性高,驗證了模型的有效性。

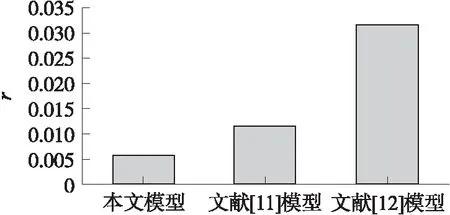
圖4 各模型皮爾森相關系數對比

3.2 模型的穩定性檢驗

沿用實驗1所建立的模型,分別隨機剔除10%,20%,40%的觀測數據的3個對比組及原觀測數據組,代入本文模型,對比總系統毀傷評估為重的毀傷概率,結果見圖5。由圖5可以看出,隨著數據的缺失率上升,折現走勢沒有出現偏差。計算得出在觀測數據缺失10%,20%,40%時,在最終時間節點總系統毀傷評估為重的毀傷概率對比完整觀測數據的模型結果分別上升了14.67%,15.04%,19.99%,說明了本文模型的穩定性。

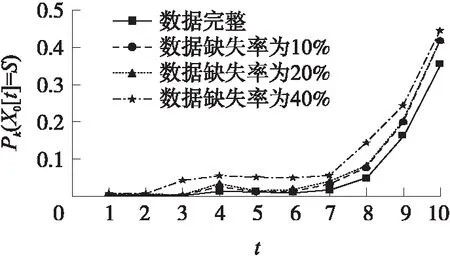
圖5 數據缺失的不同情況下本文模型的總系統毀傷評估為重的概率對比

4 結論

鑒于民用機場毀傷評估的空白,本文提出一種基于動態貝葉斯網絡的民用機場毀傷評估模型,對其有效性、穩定性檢驗的結果表明,該模型切實可行。具體結論如下:①對民用機場目標按功能進行分類,建立動態貝葉斯模型,并闡述模型運行流程。②引入蒙特卡洛法模擬毀傷實驗過程,得出實驗結果作為算例用以檢驗模型。③引入統計學中皮爾森相關系數以量化對比本文模型與現有文獻模型的結果相關程度,結果表明,本文模型較其他模型精確度提高50.83%,可證明本文模型的有效性。④通過對不同缺失率的數據代入本文模型的對比,在數據缺失率為40%時,最終結果誤差僅為19.99%,驗證了本文模型的穩定性。

[1] 朱冬生. 世界經典戰例:戰爭卷[M]. 北京:中國人民解放軍出版社,2010.

ZHU Dongsheng. World classic battles:war volume[M]. Beijing:PLA Publishing House,2010. (in Chinese)

[2] LI Chenhan. The application of Bayesian network in battle damage assessment[C]//Proceedings of 2014 IEEE the 5th International Conference on Software Engineering and Service Science. Beijing:IEEE,2014:4.

[3] MA Z,SHI Q,LI B. Battle damage assessment based on Bayesian network[C]//The 8th ACIS International Conference on Software Engineering,Artificial Intelligence,Networking,and Parallel/Distributed Computing. [s.l.]:IEEE,2007:388-391.

[4] LEFTWICH J,GRAFTON A P. Aircraft battle damage assessment and repair(ABDAR)evaluation:ADA 2003-426954[R]. Springfield,Virginia:United States Air Force Research Laboratory,2003.

[5] 李玉蘭,周彥江,尹國舉. 模糊綜合評判在戰斗損傷評估中的應用[J]. 軍械工程學院學報,2005,17(2):42-45.

LI Yulan,ZHOU Yanjiang,YIN Guoju. Application of fuzzy comprehensive evaluation in the assessment of combat damage[J]. Journal of Ordnance Engineering College,2005,17(2):42-45. (in Chinese)

[6] 王潤生,賈希勝. 基于損傷樹模型的戰場損傷評估研究[J]. 兵工學報,2005,26(1):72-76.

WANG Runsheng,JIA Xisheng. Damage tree model based battlefield damage assessment[J]. Acta Armamentarii,2005,26(1):72-76. (in Chinese)

[7] 李向東. 目標毀傷理論及工程計算[D]. 南京:南京理工大學,1997.

LI Xiangdong. Theory of target damage and engineering calculation[D]. Nanjing:Nanjing University of Science and Technology,1997. (in Chinese)

[8] 陳健,孫冀輝,米雙山. 基于貝葉斯網絡的裝備部件戰斗損傷研究[J]. 航空兵器,2005(4):6-9.

CHEN Jian,SUN Jihui,MI Shuangshan. Research of component battle damage assessment based on Bayesian network[J]. Aero Weaponry,2005(4):6-9. (in Chinese)

[9] 栗晨涵. 基于貝葉斯網絡的目標毀傷效果評估方法與建模研究[D]. 長沙:國防科技大學,2014.

LI Chenhan. Evaluation method and modeling of target damage based on Bayesian network[D]. Changsha:National University of Defense Technology,2014. (in Chinese)

[10] 曲婉嘉,徐忠林,張柏林,等. 基于貝葉斯網絡云模型的目標毀傷評估方法[J]. 兵工學報,2016,37(11):2 075-2 084.

QU Wanjia,XU Zhonglin,ZHANG Bolin,et al. Battle damage assessment method based on BN-cloud model[J]. Acta Armamentarii,2016,37(11):2 075-2 084. (in Chinese)

[11] 李京,楊根源. 動態貝葉斯網絡用于雷達遮蓋干擾效果評估[J]. 電子信息對抗技術,2012,27(2):55-59.

LI Jing,YANG Genyuan. Dynamic Bayesian network for radar masking jamming effectiveness assessment[J]. Electronic Information Warfare Technology,2012,27(2):55-59. (in Chinese)

[12] 胡匯洋,許應康,黃炎焱. 基于動態貝葉斯網絡的目標毀傷等級評估[J]. 科學技術與工程,2011,11(16):3 754-3 759.

HU Huiyang,XU Yingkang,HUANG Yanyan. Target damage rank assessment based on dynamic Bayesian network[J]. Science Technology and Engineering,2011,11(16):3 754-3 759. (in Chinese)