CTS機構幾何誤差分析及補償

張竹青，謝志江，蹇開林，緱雙雙

(重慶大學 機械傳動國家重點實驗室， 重慶　400044)

獲軌跡試驗(簡稱CTS試驗)，是研究分離體與母機安全分離特性的一項風洞模擬試驗技術。分離體模型6自由度機構(下文簡稱CTS機構[1])是CTS試驗系統的核心，通過控制實現分離體模型6個自由度的運動(X，Y，Z，偏航，俯仰，滾轉)。CTS機構的精度是整個CTS試驗準確性和可靠性的保障，為提高精度，需要對引起末端位姿誤差的各項因素進行分析研究，以達到對末端位姿誤差進行補償的目的，從而提高運動精度。

CTS機構從本質上來說是一個6自由度的機械手[2]。對CTS機構來說，運動精度分為兩種[3]：重復定位精度和絕對定位精度。一般情況下，重復定位精度高于絕對定位精度[4]。隨著我國綜合國力的增強和新型飛行器研制技術的快速發展，對CTS試驗也提出了更高的要求[5]。之前研制的CTS機構，由于當時的科學條件限制難以滿足當前飛行器研制的需求。近年來，飛行器的研制和改型任務日益繁重[6]，迫切需要研制新型的CTS試驗系統，提高其可靠性和相關性能。本課題組研制開發的CTS機構將用于風洞捕獲軌跡試驗，完成相關的試驗項目。

CTS機構的誤差補償采用參數誤差直接修正的方法，通常實際參數與理論參數存在差異，從而導致末端執行器產生運動誤差。可通過參數標定求出實際參數，然后修改理論值，減小實際值與理論值之間的差異，讓運動學模型盡量接近真實情況，最后利用修正過的運動學公式求解驅動值，從而達到減小末端位姿誤差的目的。

1　CTS系統坐標系定義

本文對CTS機構誤差分析分為兩部分：一是機構幾何誤差分析；二是機構零位誤差分析。在誤差分析前需要先建立坐標系，在該機構的誤差分析及補差過程中涉及風洞固定坐標系、分離體體軸坐標系、天平坐標系和CTS機構總體坐標系。

1.1　風洞固定坐標系Oxdydzd

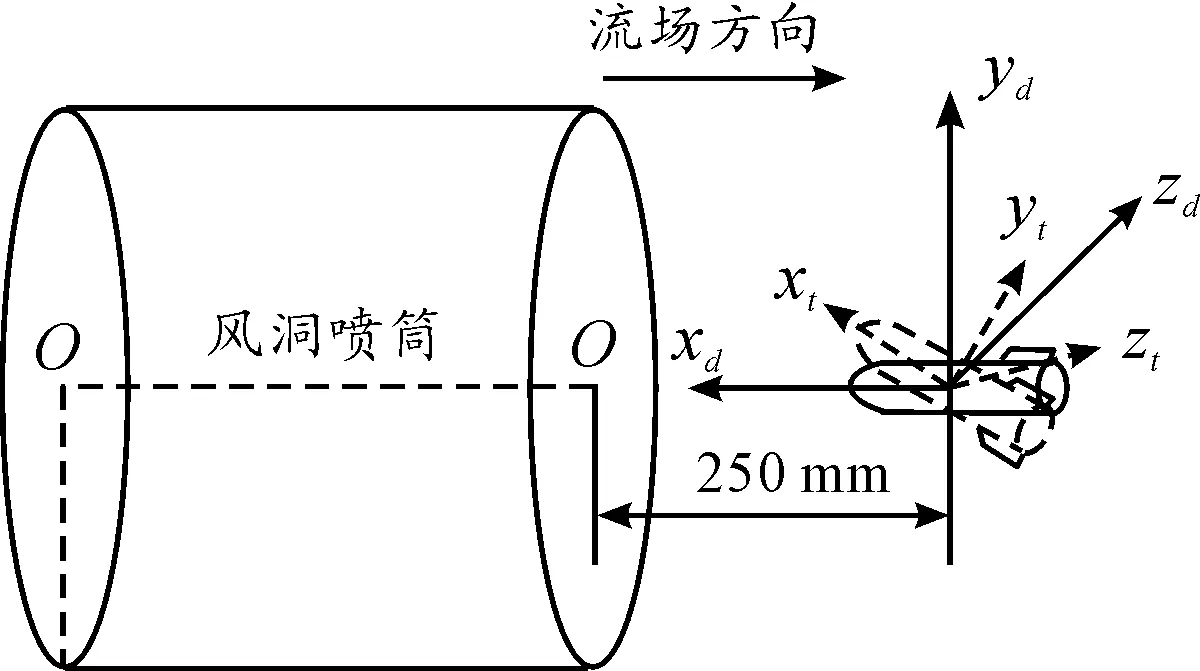
圖1　風洞固定坐標系與體軸坐標系定義

風洞固定坐標系Oxdydzd是整個捕獲軌跡試驗的參考坐標系，不隨模型的轉動而轉動。其原點在風洞噴管端面前250 mm處，位于風洞試驗段縱軸上；xd軸沿著試驗段縱軸，逆氣流方向為正；yd軸位于試驗段縱對稱平面內，垂直縱軸向上為正；zd軸垂直于縱對稱面，從逆氣流方向看，向右為正。風洞固定坐標系如圖1所示。

1.2　分離體體軸坐標系Oxtytzt

分離體體軸系Oxtytzt的原點位于分離體模型的理論質心。xt軸平行于分離體模型的前行方向；yt軸在分離體模型縱對稱平面內垂直于xt軸，方向向上為正；zt軸垂直于分離體模型縱對稱面，方向向右為正。分離體體軸坐標系如圖1所示。

1.3　天平坐標軸系Oxyz

天平坐標軸系Oxyz是固定在天平上的坐標系。其原點O為天平的力矩參考點；x軸沿天平原點中心線指向模型端；y垂直于Ox軸，在天平縱對稱面內，向上為正；z軸可用右手定則確定

1.4　機構總體坐標系Oxzyzzz

機構總體坐標系Oxzyzzz原點O為尾支桿長度為設計長度500 mm處的末端點，總體坐標系不隨機構的運動而改變，固定在空間中。沿著尾支桿軸線向外的方向為xz軸正向；yz軸向上為正；zz軸可用右手定則確定。該坐標系與尾支桿等于原長時的天平坐標系重合，當尾支桿長度變化時，天平坐標系會隨之改變，而CTS機構總體坐標系的位置不變。

2　CTS機構幾何誤差分析

給定機構指令位置，逆解求出驅動值，驅動機構運動，則實際位置和指令位置有偏差。需要對機構的轉換矩陣Tz調整，使得計算的正解位姿與實際正解位姿盡可能接近。再通過調整后的正解方程反解出逆解方程，給定指令位姿，驅動機構運動，則最終的實際位姿與指令位姿更加接近。

加工幾何誤差引起的位姿誤差值可由式(1)計算。

ΔXz=ΔTzq

(1)

其中：ΔXz代表末端位姿誤差列向量；q代表機構輸入值，為各驅動滑塊滑移距離；ΔTz表示位姿誤差矩陣。將式(1)展開成矩陣形式有

(2)

式(2)中ΔT11、ΔT12、ΔT21、ΔT22均為3×3的矩陣。ΔT11表示機構X、Y、Z向導軌與機構總體坐標系的坐標軸線xz、yz、zz軸不平行導致的位置誤差矩陣；ΔT12和ΔT22分別表示由機構實際偏航、滾轉軸線分別與機構總體坐標系yz軸、zz軸不重合而引起的位置誤差矩陣和姿態誤差矩陣。為簡化誤差計算過程，在實際中確定機構總體坐標系時，按照滾轉軸線的方向來確定zz軸的方向。ΔT21表示直線滑塊驅動引起的姿態角誤差矩陣，由于實際中機構位置的變化不會引起姿態角的變化，因此ΔT21為零矩陣。

2.1　導軌與總體坐標系軸線不平行誤差分析

理論情況下，實現末端分離體模型平動的3根導軌X、Y、Z分別與機構總體坐標系的xz軸、yz軸、zz軸平行，末端的3個位移是解耦的，因此驅動X向滑塊沿著X直線導軌滑移只會引起分離體模型xz向的位移，同理，驅動Y、Z方向的滑塊只會引起分離體模型相應方向的位移。但是實際加工出來的機構存在導軌與機構總體坐標軸不平的情況，那么機構末端3個方向的位移與滑塊的滑移距離就不再是解耦的，而是相互耦合在一起。分離體模型理論質心3個方向的誤差分別設為Δx、Δy、Δz，則將導軌與坐標軸不平行導致的誤差寫成矩陣形式可表示為

(3)

結合式(2)，有

(4)

這一部分的誤差辨識可以考慮用最小二乘法多項式擬合[7]來確定。通過分別測量機構X、Y、Z單軸運動的數據，擬合出驅動滑塊滑移距離和分離體模型理論質心位移誤差之間的曲線關系，得到擬合函數，即可辨識出導軌與軸線不平行引起的誤差矩陣ΔT11。

2.2　偏航和俯仰軸線與總體坐標系軸線不重合誤差分析

當偏航和俯仰軸線與機構總體坐標系yz軸或zz軸不重合時，機構繞偏航軸或者俯仰軸運動時，會引起分離體模型理論質心平動的位置誤差和繞軸線轉動的姿態誤差。

2.2.1位置誤差分析

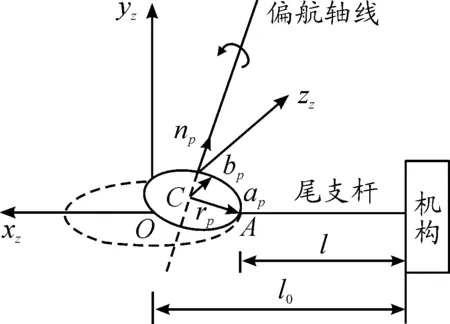
圖2　偏航軸線偏移示意圖

理想情況下偏航軸線和機構總體坐標系的yz軸是重合的，繞著偏航軸線的偏轉，尾支桿末端的天平校心運動軌跡為圓O上的一段圓弧。但實際情況中，由于加工裝配誤差存在，兩軸線不重合，那么機構繞著偏航軸旋轉時會引起機構天平校心沿著圓C的圓弧運動，如圖2所示。

坐標系Oxzyzzz為機構總體坐標系，尾支桿理論長度為l0，實際長度為l。在理想的情況下，當機構繞著yz軸偏航ψ時，天平校心的理論位置為

(5)

在實際情況中，天平校心運動軌跡所在圓C的圓心坐標為(c1p,c2p,c3p)，法向量為np，半徑為rp，對應圓C的參數方程[8-9]為

(6)

其中：(a1p,a2p,a3p)與(b1p,b2p,b3p)分別對應單位向量a和b，它們相互垂直又垂直于np；ψ表示繞著偏航軸yz轉過的角度，隨著ψ的變化，可以求出實際天平校心在機構總體坐標系中的位置。

偏航軸線偏移引起的天平校心的位置誤差值可表示為：

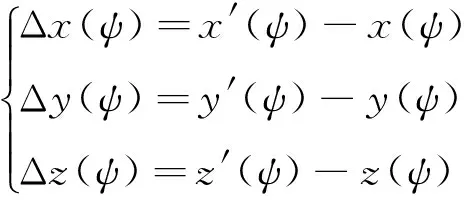
(7)

俯仰軸線偏移對應見圖3。

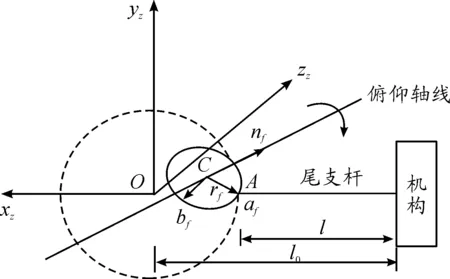
圖3　俯仰軸線偏移示意圖

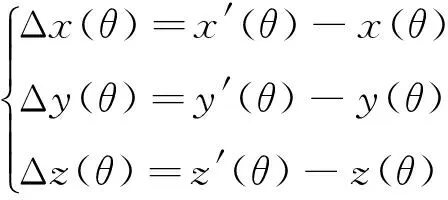
(8)

由于實際機構滾轉軸線和機構總體坐標系xz軸線重合，因此機構滾轉運動不會引起天平校心位置的運動。

理論偏航角和俯仰角分別是偏航、俯仰驅動滑塊滑移距離的函數，即ψ=f(qp)，θ=f(qf)。綜上分析，偏航俯仰軸線偏移引起天平校心的位置誤差為

(9)

2.2.2姿態誤差分析

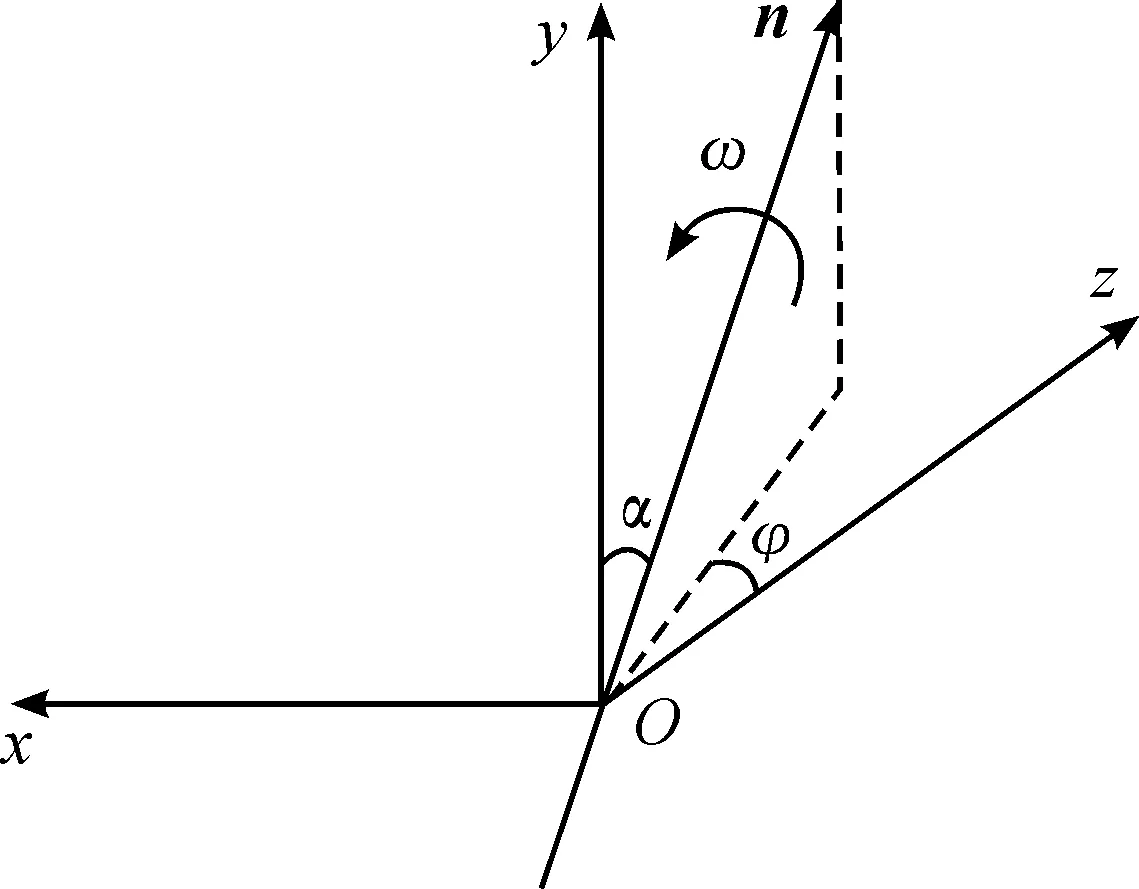
圖4　剛體轉動示意圖

由于偏航、俯仰軸線與機構總體坐標系的yz軸、zz軸有微小的傾角，因此偏航軸線的偏航運動實際上會引起分離體模型在機構總體坐標系中偏航、俯仰和滾轉，俯仰時相同。

機構實際繞偏航、俯仰軸運動時，相當于已知了偏航、俯仰軸的軸線方向以及轉角大小，然后求解分離體模型在總體坐標系轉過的角度。

任意個剛體的轉動可以用定軸轉動的轉軸轉角參數(球坐標)來描述，也可以使用姿態角來描述。那么軸線偏移對應的情況是已知分離體模型的轉軸轉角參數求解姿態角。

如圖4所示：n表示實際軸線方向的單位矢量；ω為轉過的角度；(α,φ)為矢量n的球坐標角。轉動R球坐標描述為

(10)

其中：

cω=cosω,sω=sinω,cφ=cosφ,sφ=sinφ,cα=cosα,sα=sinα

轉動姿態角描述為

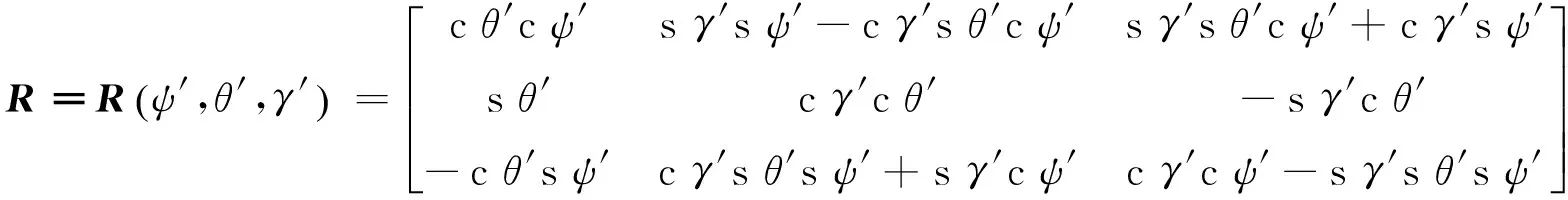
(11)

其中：

cθ′=cosθ′,sθ′=sinθ′,cψ′=cosψ′,sψ′=sinψ′,cγ′=cosγ′,sγ′=sinγ′

由式(10)與(11)中的元素對應相等求出實際的ψ′、θ′、γ′。

對于偏航軸線與yz軸不重合引起的誤差為

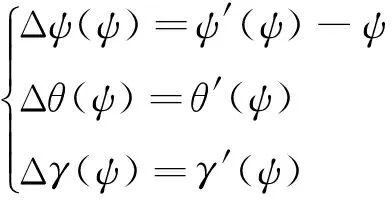
(12)

對于俯仰軸線與zz軸不重合引起的誤差為

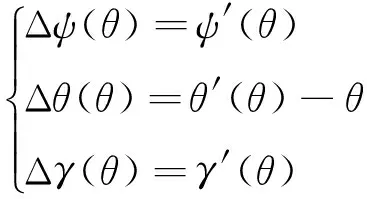
(13)

因此，由偏航和俯仰軸線與機構總體坐標系軸線不重合引起的姿態誤差可表示為

(14)

2.3　機構零位誤差分析

采用CTS機構運動學方程求分離體模型位置和姿態與CTS機構驅動滑塊滑移距離之間的關系，分離體模型的位置和姿態必須放在特定的坐標系中。在理想情況下，風洞坐標系與CTS機構總體坐標系重合。

在實際情況中，風洞固定坐標系是通過噴管的位置確定的，機構總體坐標系是由機構確定的，這2個坐標系不會完全重合，即當CTS機構未運動處于機構零位時，分離體模型在風洞固定坐標系中的位姿已經有初值，所以在誤差補償時需要對機構的零位進行補償。

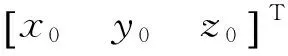
3　機構幾何誤差補償試驗研究

3.1　數據采集與處理

3.1.1單軸運動數據測量與分析

針對加工好的機構，需要對機構單軸運動時的重復定位精度和絕對定位精度進行測量。對長度為500 mm的尾支桿，末端固定粘貼一個靶標，單軸運動，利用激光跟蹤儀測量點的位置，在計算機測量軟件中記錄下來。X、Y、Z方向每100 mm記錄1個點的數據，由于數據量很大，在此就不一一列出。

按照設計，單軸驅動X滑塊時，末端測量點的yz和zz不應產生位移值，則實際產生的位移值也就是Y和Z方向的誤差值，用δx(qx)、δy(qx)、δz(qx)分別表示單軸驅動X方向運動時對X方向、Y方向、Z方向產生的誤差值。此處將測量數據利用Matlab繪制出誤差曲線，如圖5～9所示，圖中δj(qi)表示驅動i方向的滑塊引起的jz方向的位移誤差。單軸驅動Y和Z方向時同理。

通過數據分析，可得到CTS機構單軸運動時各軸的重復定位精度和絕對定位精度值，見表1和表2。

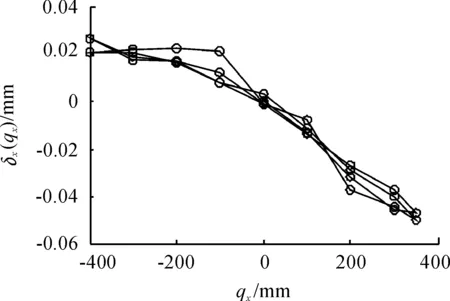
圖5　X滑塊滑動引起質心xz向位移誤差

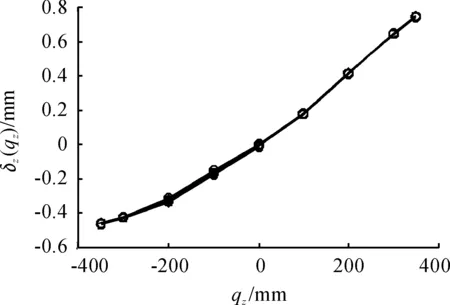
圖7　Z滑塊滑動引起質心zz向位移誤差

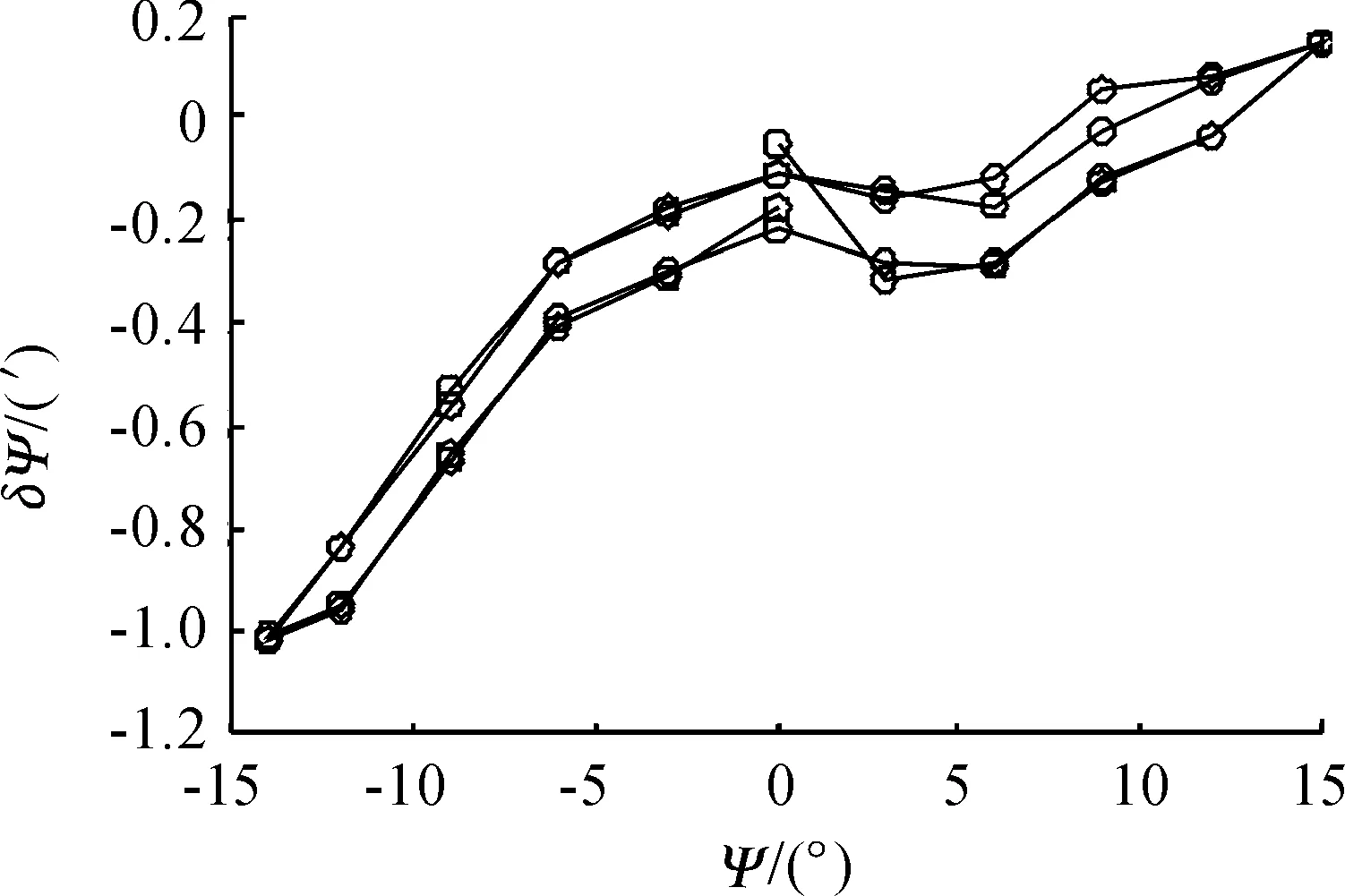
圖9　偏航角度誤差值

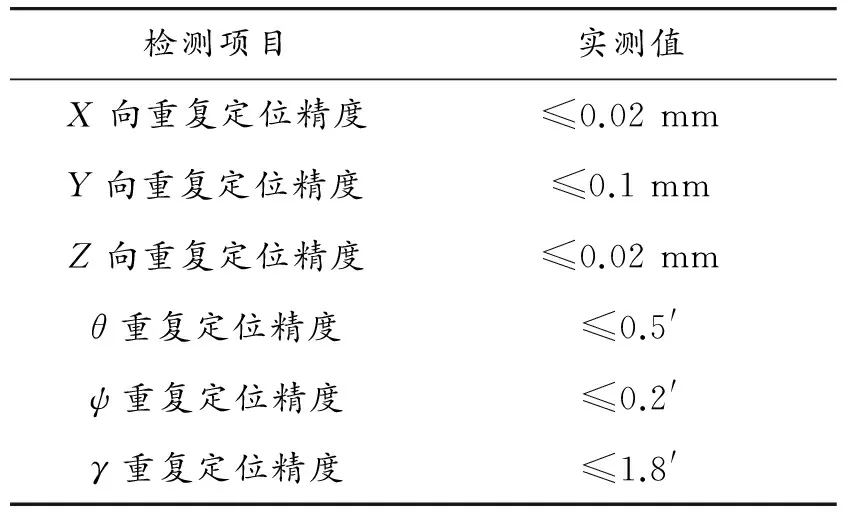
檢測項目實測值X向重復定位精度≤0.02mmY向重復定位精度≤0.1mmZ向重復定位精度≤0.02mmθ重復定位精度≤0.5'ψ重復定位精度≤0.2'γ重復定位精度≤1.8'

表2　CTS機構絕對定位精度

將表1中的測量值和允許值比較，只有滾轉角γ的重復定位精度不夠，其原因主要是測量方法本身引起的誤差過大。測量時，靶標貼在尾支桿安裝端面上，在滾轉電機驅動下，靶標開始轉動，通過前后2次運動靶點的位置坐標來計算滾轉角。這種測量方式由于靶點經過的圓弧太小，測量數據的測量誤差對計算出的滾轉角影響較大，因此需要改進測量方法，增大滾轉的圓弧半徑。

將表2測量值和允許值比較，單軸驅動時只有Z向的定位精度不滿足要求。考慮各項誤差產生的運動誤差的累加效應，仍需對單軸驅動進行誤差補償。

3.1.2零位測量

在建立好風洞固定坐標系和CTS機構總體坐標系后，進一步可以通過激光跟蹤儀測量和計算出機構總體坐標系的初始零位，初始零位位姿見表3。表3中：x0、y0、z0表示機構總體坐標系在風洞固定坐標系中的位置；ψ0、θ0、γ0表示從風洞固定坐標系旋轉到機構總體坐標系的姿態角。

表3　初始零位位姿

3.2　誤差補償

數據測量完后需要對補償效果進行驗證。在正逆解程序中加上零位，給定末端點在風洞固定坐標系中的位姿，控制器驅動機構運動到實際位姿，利用激光跟蹤儀測量實際位姿，計算補償前定位誤差；將控制器中的程序改為補償后的程序，給定同樣的位姿，測量機構達到的位姿，計算補償后的定位誤差；前后對比，驗證補償效果。

機構單軸誤差可由上述方法來標定，由于測量數據重復性比較好，可以采用最小二乘法多項式擬合求出誤差函數。單軸運動誤差擬合曲線見圖10～12，圖中橫坐標表示滑塊滑移距離，縱坐標δj(qi)表示驅動i方向的滑塊滑動引起的質心在總體坐標系中jz方向的位移誤差值。

圖10　δx(qi)誤差擬合曲線

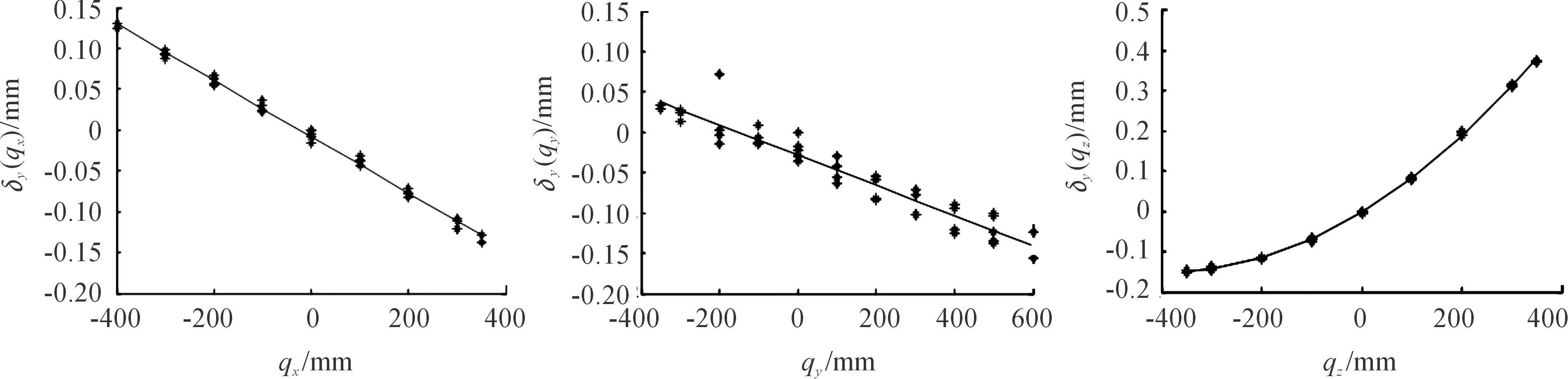
圖11　δy(qi)誤差擬合曲線

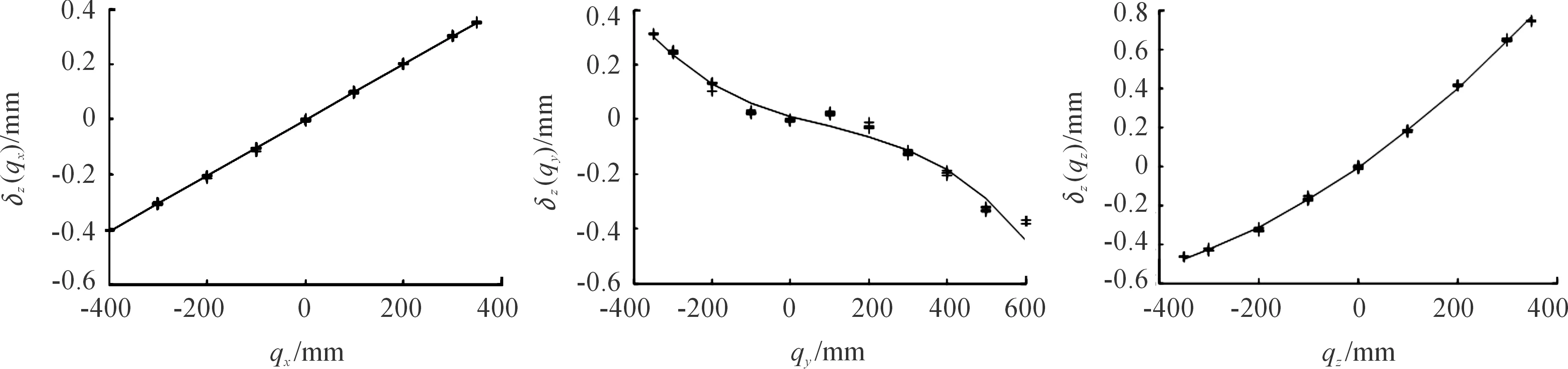
圖12　δz(qi)誤差擬合曲線

通過最小二乘法擬合出的誤差曲線圖對應的誤差函數分別如下：

(15)

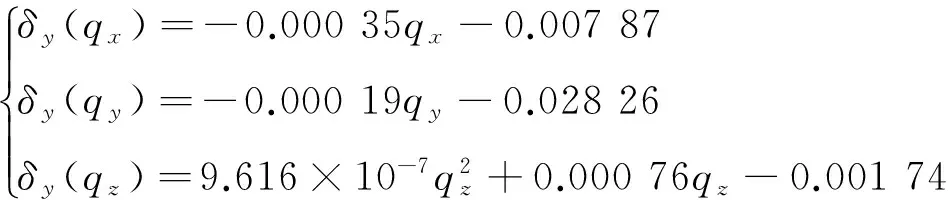
(16)

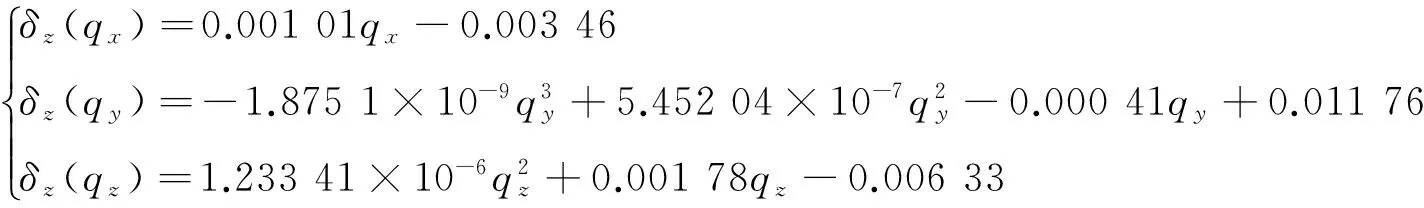
(17)

那么，式(3)中的導軌與軸線不平行而導致的誤差為

(18)

機構三軸聯動誤差在CTS機構總體坐標系原點處，因此將式(18)以及測試出的機構總體坐標系和風洞固定坐標系之間的零位數據代入相應正解方程中，便可得到補償后的正解。

補償后的逆解需要通過正解方程反求輸入的滑塊位移，過程為求解3個三元方程組成的非線性方程組，將方程組寫成一般形式編入CTS機構控制器軟件中，同時添加求解非線性方程組的牛頓迭代法[10-11]，即可完成CTS機構逆解的求取。

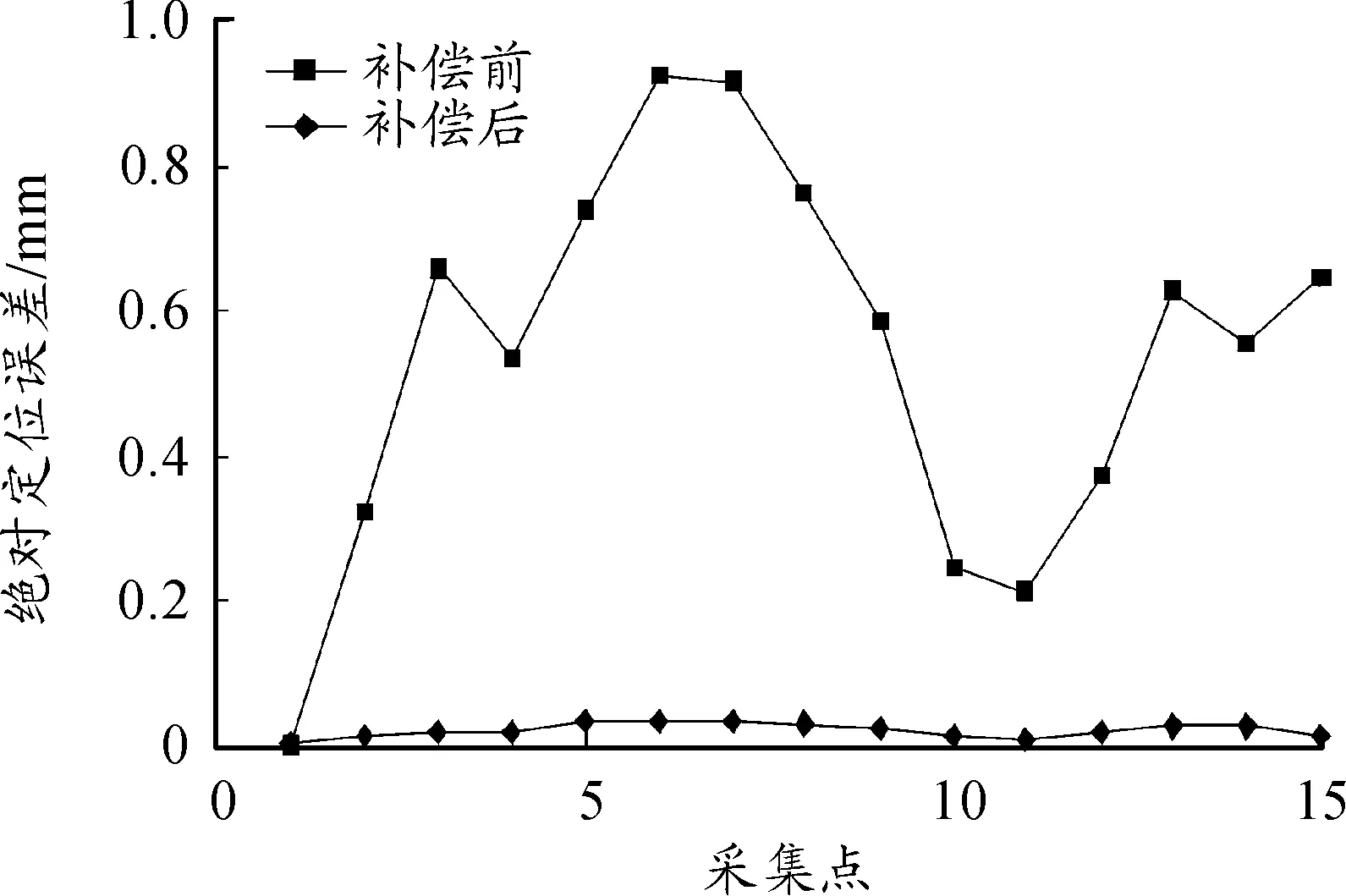
圖13　三軸聯動補償前后絕對定位精度對比

為了驗證誤差補償的結果，通過測量X、Y、Z三軸聯動來檢測導軌與機構總體坐標系軸線不平行的誤差方法的有效性。

未補償前，給定空間15個點的位置，通過控制軟件中的逆解程序計算并驅動機構運動，記錄最終模型理論質心在風洞固定坐標系中的位置(已補償零位)，將給定位置和最終達到的位置記錄下來。給定同樣的位置，利用補償后(補償零位及導軌與軸線不平行誤差)的逆解驅動機構運動，將補償后實際到達的位置記錄下來。根據2次的記錄，計算出補償前后的定位誤差，如表4所示，將補償前后的定位誤差繪制成曲線圖，如圖13所示。

由圖13可知：CTS機構的3軸聯動絕對定位精度得到了明顯的提高，補償前絕對定位誤差的最大值為0.952 2 mm，補償后絕對定位誤差的最大值為0.112 3 mm，絕對定位精度提高了88.21%。

表4　三軸聯動誤差補償前后絕對定位精度(mm)

4　結束語

本文對CTS機構的幾何誤差進行了詳細的理論分析，通過實驗測試得到數據，并采用最小二乘法擬合辨識了導軌與軸線不平行引起的運動誤差，通過理論分析求解了偏航俯仰軸線偏移的誤差矩陣，將辨識出的誤差矩陣引入到正解方程中，得到補償后的正解方程。利用牛頓迭代法求取補償后的正解方程組成的非線性方程組，得到補償后的逆解。通過對補償試驗現場測量相關數據的分析，利用本文研究的補償方法，采用軟件補償法完成了CTS機構的幾何誤差補償。通過X、Y、Z三軸聯動比較了補償前后CTS機構的定位誤差，驗證了補償方法的可靠性。

參考文獻：

[1]緱雙雙，蹇開林.一種六自由度分離體機構運動學分析及仿真[J].重慶理工大學學報(自然科學)，2017，31(5)：43-48.

[2]YOSHIKAWA J.Manipulability of Robotic Mechanisms[J].Int J Robotics Reserch，1987，4(2)：3-9.

[3]王東署，遲健男.機器人運動學標定綜述[J].計算機應用研究，2007，24(9)：8-11.

[4]王東署.工業機器人標定技術研究[D].沈陽：東北大學，2006.

[5]黃敘輝，羅新福.FL-24風洞新型捕獲軌跡系統設計與發展[J].空氣動力學報，2008，26(2)：145-149.

[6]黃敘輝，龐旭東，等.1.2 m跨超聲速風洞新型捕獲軌跡系統研制[J].實驗流體力學，2008，22(2)：95-98.

[7]李蓓蕾.多次自適應最小二乘曲線擬合方法及其應用[D].荊州：長江大學，2014.

[8]路元鴻.三維空間中圓的參數方程[EB/OL].[2017-03-08].http://www.mathchina.net/dvbbs/dispbbs.asp?boardid=3&Id=471.

[9]李養成，郭瑞芝.空間解析幾何[M].北京：科學出版社，2004.

[10] 王開榮，楊大地.數值分析[M].北京：高等教育出版社，2010.

[11] 徐建強.并聯機構中常用的數學分析法[J]. 農業裝備技術，2010(5)：20-21.