以游戲為載體　發(fā)展思維能力
——《棋盤上的奧秘》教學(xué)設(shè)計與思考

朱姍姍

【教學(xué)內(nèi)容】自編素材。

【教學(xué)過程】

一、回顧微課內(nèi)容，引出課程中心

在授課前一天，學(xué)生已在家觀看微課《棋盤上的奧秘》，內(nèi)容為：紅紅和明明兩人在12×12的棋盤上下棋，從右下角開始，兩人輪流下，只能下在前一顆棋子的左上方距離一格或兩格處，先搶到左上角的終點者獲勝。紅紅（執(zhí)白）三局都獲勝。（圖1）

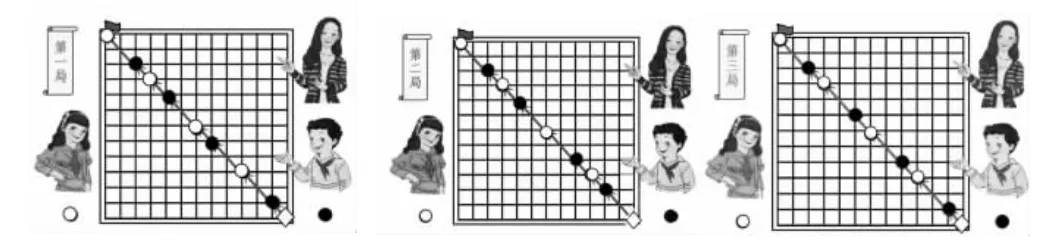
圖1　微課截圖

1.回顧微課，定義必勝點。（圖2）

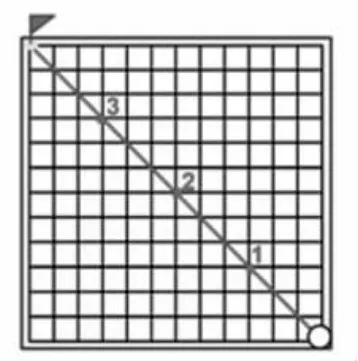
圖2

討論“為什么紅紅三局都能贏？”得出“只要搶到3號點，不管對手下1格還是2格都能保證自己搶到終點”從而定義“不管對手如何下，都能保證必勝的點”為必勝點。

2.初步感受倒推，規(guī)范必勝策略的表達。

討論“想要搶到3號點，又得下到哪些點？”得出“想要下到3號點，必須搶到2號點；想要搶到2號點，必須搶到1號點。”

小結(jié)：用倒推的方法可以找出所有的必勝點。在這個棋盤上，要后下、下必勝點，才能獲勝。

【設(shè)計意圖：這部分內(nèi)容是整堂課的準(zhǔn)備環(huán)節(jié)。有以下幾個意圖：1.在微課中演示12×12棋盤及相應(yīng)游戲規(guī)則的操作，便于學(xué)生熟悉棋盤，理解8×8棋盤的游戲規(guī)則；2.引出在一維線上進行逆向推理的核心問題；3.定義了必勝點并規(guī)范必勝策略的說法，使學(xué)生后續(xù)作答更具指向性。】

二、利用8×8的棋盤，在對弈中感悟嘗試和倒推

1.理解規(guī)則。

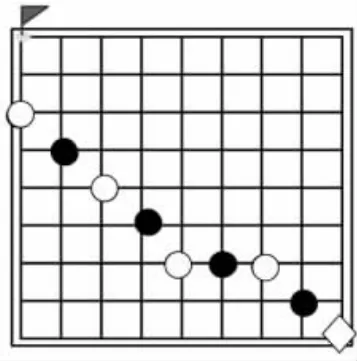
圖3　師生對弈

展示題目：在8×8棋盤的右下角放一顆棋子，以它為起點，兩人輪流在這個棋盤上下棋，規(guī)定只能下在前一顆棋子的上面、左面或者左上方距離一格處，先占領(lǐng)左上角者獲勝。

（1）師生對弈兩步：如果我的第一顆棋子下在這里，那么你的棋子可以下在哪里？

（2）師生對弈一局（教師執(zhí)白，學(xué)生執(zhí)黑），學(xué)生在“老師下到距離終點2格處點”時認輸。（圖3）

（3）討論：老師下到哪個點的時候你覺得老師一定能贏，為什么？

生：老師下到距離終點兩格處的點時一定贏了，因為我只能往上一格，而老師則會搶到終點。

【設(shè)計意圖：因有12×12棋盤游戲的微課學(xué)習(xí)，學(xué)生對8×8棋盤上的游戲規(guī)則比較容易理解。同時加入師生對弈環(huán)節(jié)，是為了保證全班學(xué)生都能掌握游戲規(guī)則，感知必勝點，為頓悟用“倒推法”找必勝點做鋪墊。】

2.探索必勝策略。

布置任務(wù)：在練習(xí)紙的對弈區(qū)，和你的同桌對弈，你下到哪個點的時候覺得自己肯定能贏，把這樣的點記錄在必勝點記錄區(qū)。

【設(shè)計意圖：在這里，我們給予學(xué)生充分的對弈體驗，讓學(xué)生在對弈中萌生博弈觀念，初步形成倒推思路。】

3.反饋：討論各個點是否為必勝點。

（1）錯誤點。（圖4）

生：下到這個點，如果對手往上，我可以往左上，搶到終點；如果對手往左上，我就直接往上搶到終點。

生：（反駁）下到這個點，如果對手往左，我就只能往上，這樣終點就被對手搶到，所以它不是必勝點。

小結(jié)：要考慮對方下棋的各種可能。

（2）往下、往右倒推點。（圖5、圖6）

生：如果我搶到這個點（圖5），對手就只能往上，我就能搶到終點。

生：如果我搶到這個點（圖6），對手就只能往左，我就能搶到終點。

（3）右下倒推點。（圖7）

生：這個點（插小旗的點）是必勝點，如果對方往左走，那我也往左，就可以搶到1號必勝點；如果對方往上，那我也往上，就可以搶到2號必勝點；如果對方往左上，那我也往左上，就直接搶到終點。也就是說只要我搶到這個點，不管對手往哪個方向下，我都能搶到終點。（學(xué)生說完后請兩位學(xué)生再把右下倒推點的驗證過程說一遍）

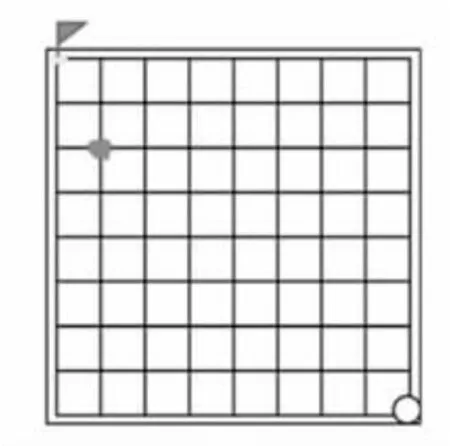
圖4　錯誤點

圖5　往下倒推點

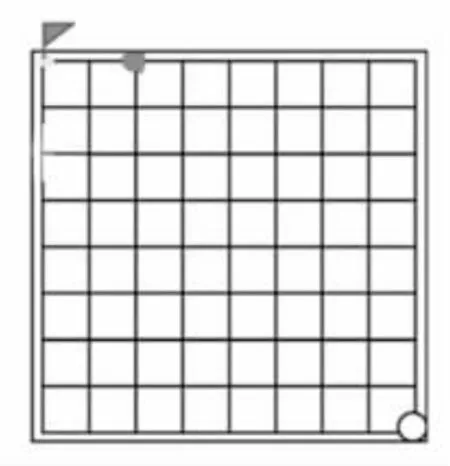
圖6　往右倒推點

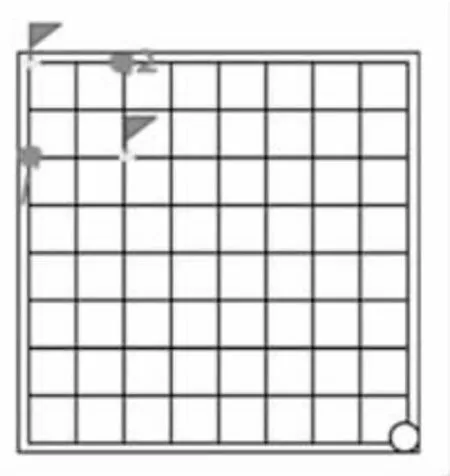
圖7　右下倒推點

【設(shè)計意圖：學(xué)生的對弈過程，實際上是一個嘗試錯誤的過程。這里的反饋分為三個層次，第一個層次，反饋錯誤點，讓學(xué)生再次明確，下棋是一種博弈，在想往對自己有利的方向發(fā)展時，對手也是這么想的，只有“不管對手如何下，都能保證必勝”的點才是必勝點；第二個層次，往右、往下的必勝點推導(dǎo)，為反饋右下必勝點做鋪墊；第三個層次，右下必勝點推導(dǎo)，稍有難度，通過多次復(fù)述推理過程，讓學(xué)生充分感悟推理的嚴(yán)密性。】

4.帶領(lǐng)倒推。

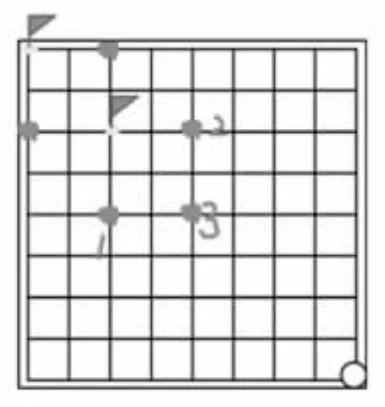
圖8

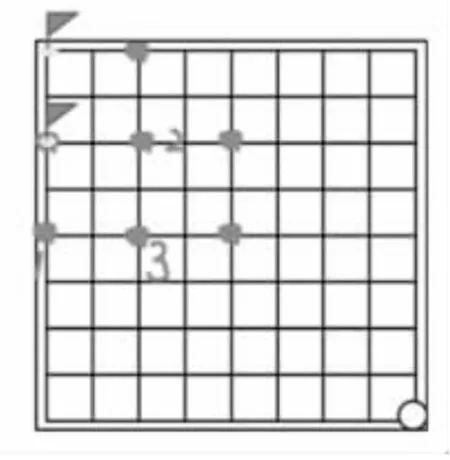
圖9

（1）討論：怎么才能搶到這個點？（圖7）

①依次根據(jù)對手的各種走法說出自己的應(yīng)對策略，得出必勝點。

②把這個點當(dāng)成終點，沿“田”字直接倒推出這三個點。（圖8）

（2）沿“田”字倒推能搶到這個點（插小旗的點）的必勝點。（圖9）

【設(shè)計意圖：在之前的學(xué)習(xí)中，學(xué)生已明白可以用倒推法尋找必勝點，但如何使用倒推法，仍有一定的難度。這一環(huán)節(jié)是基于學(xué)情的帶領(lǐng)倒推，這里要反饋兩種倒推方式：一是邊嘗試錯誤邊倒推→對前一環(huán)節(jié)的再一次嘗試和鞏固；二是建立模型后的倒推→類比倒推，建立模型，學(xué)會簡化。】

5.學(xué)生自主找必勝點。

【設(shè)計意圖：有了前面的帶領(lǐng)倒推，學(xué)生對全盤倒推有了一定的感知，這時候再次讓學(xué)生找必勝點，能夠水到渠成。】

6.師生對弈兩局。（均學(xué)生贏）

學(xué)生反饋必勝策略：想要搶到這個點，必須搶到這個點；想要搶到這個點，必須搶到這個點……從終點開始往起點倒推就可以了。所以必勝策略是后走，走必勝點。（圖10）

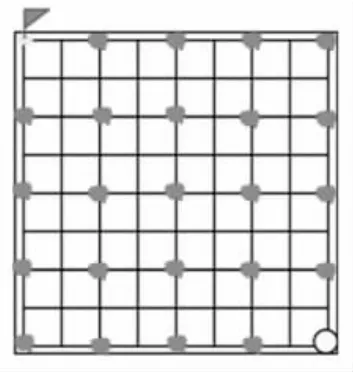
圖10

【設(shè)計意圖：贏了教師極大鼓舞了學(xué)生，并使學(xué)生獲得了數(shù)學(xué)學(xué)習(xí)的成就感。此環(huán)節(jié)通過規(guī)范語言，經(jīng)歷推理過程，領(lǐng)悟“倒推”原理。】

7.小結(jié)：為了找到這個棋盤上的必勝策略，我們先嘗試找出離終點最近的三個必勝點，再從終點開始，往起點倒推。找完必勝點之后，老師和這位同學(xué)對弈，其實就是在驗證大家的必勝策略是否正確。

三、出示5×5棋盤，運用策略，鞏固方法

游戲規(guī)則相同，找出5×5棋盤的必勝點，并根據(jù)必勝點確定必勝策略。

反饋：必勝點（圖11）；必勝策略：先走，走必勝點。

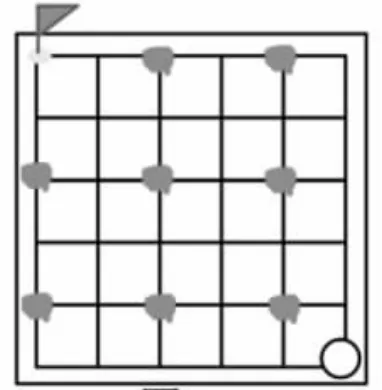
圖11

【設(shè)計意圖：這一環(huán)節(jié)主要鞏固倒推的方法，讓學(xué)生將初步探索到的策略在變化了的情境中加以運用，在培養(yǎng)學(xué)生推理能力的同時鍛煉其語言表述的能力。】

四、出示 8×8－5×5 棋盤，引發(fā)認知沖突

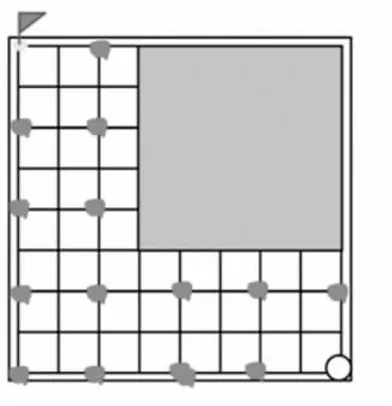
圖12　學(xué)生推導(dǎo)必勝點

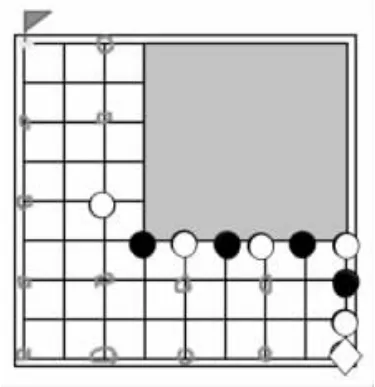
圖13　師生對弈

1.同樣的游戲規(guī)則，自行找出 8×8－5×5 棋盤的必勝策略。

2.反饋。（圖12）

3.師生對弈驗證，學(xué)生輸。（圖13，教師執(zhí)白，學(xué)生執(zhí)黑）

討論：已找到必勝點，為什么會輸？

生：沒考慮老師往上走，必勝策略有誤。

小結(jié)：我們用驗證的方法發(fā)現(xiàn)必勝策略是有漏洞的，說明在倒推的過程中還需要考慮對手下棋的各種可能，讓自己的思維更嚴(yán)謹(jǐn)、更全面。

【設(shè)計意圖：學(xué)習(xí)了前面的知識，學(xué)生會產(chǎn)生思維定勢，以為只要進行“田”字倒推即可，這一環(huán)節(jié)讓學(xué)生產(chǎn)生了強烈的認知沖突，從而促進學(xué)生反思：1.得出必勝策略后要進行驗證；2.倒推時務(wù)必嚴(yán)密。這一環(huán)節(jié)，既讓學(xué)生體驗了反思的重要意義，又感受到完整的解決問題的過程。】

五、回顧所學(xué)，全課小結(jié)

師：在今天這堂課上，你有什么新的收獲？

生：在尋找策略的時候我們可以先嘗試一下，找找感覺。

生：學(xué)會了用倒推去解決數(shù)學(xué)和生活問題。

生：思考問題要嚴(yán)密。

生：倒推后的順向驗證能幫我們驗證倒推結(jié)果是否正確。

【課后回望】

本課例是一節(jié)數(shù)學(xué)活動課。學(xué)生在充分的活動中積累經(jīng)驗，教師進行適時的引導(dǎo)，使學(xué)生頓悟出方法的選擇。在討論中掌握方法的使用，并理解數(shù)學(xué)本質(zhì)。

本課設(shè)計有以下幾個特點：

一、材料創(chuàng)設(shè)符合學(xué)生興趣

本課例采用學(xué)生十分喜愛的下棋游戲，學(xué)生興趣高漲，求知欲強烈。從 8×8，5×5 到 8×8－5×5，棋盤在不斷地演變，學(xué)生也在層次遞進的材料引導(dǎo)下不斷地觸碰他們的“最近發(fā)展區(qū)”，從原來沒有一個學(xué)生能夠解決問題到最后幾乎每位學(xué)生都至少能夠解決8×8的棋盤，不同程度的學(xué)生都有不同層次的收獲。

二、過程展開注重自主嘗試

在課堂上，教師放手讓學(xué)生通過不斷地出錯，在嘗試中進行自我糾錯、反思和辨正。在師生、生生之間對弈，獲得充分的感知經(jīng)驗后，再經(jīng)過教師的引導(dǎo)，自發(fā)地“頓悟”：可以使用倒推策略解決問題。學(xué)生對倒推法的選擇有了深刻的體驗。

三、引導(dǎo)介入尊重契合學(xué)情

盡管在獲得充分感知經(jīng)驗后，學(xué)生已經(jīng)頓悟可以用倒推法解決問題，但如何使用倒推法進行必勝策略的推導(dǎo)，學(xué)生仍有困難，需要教師的及時引導(dǎo)。教師抓準(zhǔn)時機，在學(xué)生的討論中適時地進行方法點撥，讓學(xué)生再次對方法的使用有所頓悟。這樣的流程設(shè)計，既給了學(xué)生充分自主學(xué)習(xí)的空間、又尊重學(xué)情，既開放、又扎實。

四、教學(xué)推進關(guān)注策略與能力

本課例中，每一個過程設(shè)計都有明確的設(shè)計意圖，將課時整體目標(biāo)細化為環(huán)節(jié)目標(biāo)。盡管材料不斷演變，目標(biāo)細化延展，但每一個材料和過程展開都緊緊圍繞博弈思想、倒推方法，并將最大的“力氣”用在培養(yǎng)學(xué)生的推理能力上。

授課后，我們也一直在思考棋盤的材料是否有更多可挖掘和探索的地方，也得到了很多教師的建議：如將規(guī)則改成只能往上或往左走，那么必勝策略會怎樣？這時候必勝策略的得出，除了可以在棋盤上倒推，還可以將8×8棋盤上的路線拉成一條能走16步的一條線段，此時棋盤就和搶數(shù)游戲完全相通了，方法和策略也在不同的材料中延伸貫通。