概率綜合演練B 卷

■吳傳葉

一、選擇題

1.道路交通法規(guī)定：行人和車(chē)輛路過(guò)十字路口時(shí)必須按照交通信號(hào)指示通行,綠燈行,紅燈停,遇到黃燈時(shí),如已超過(guò)停車(chē)線需繼續(xù)行進(jìn)。某十字路口的交通信號(hào)燈設(shè)置時(shí)間是：綠燈48 s,紅燈47s,黃燈5s。小張是個(gè)特別守法的人,只有遇到綠燈才通過(guò),則他路過(guò)該路口不等待的概率為( )。

A.0.95 B.0.05

C.0.47 D.0.48

2.從含有質(zhì)地均勻且大小相同的2個(gè)紅球,n個(gè)白球的口袋中隨機(jī)取出1個(gè)球,若取到紅球的概率是,則取到白球的概率等于( )。

3.圖1是半徑分別為1,2,3的三個(gè)同心圓,現(xiàn)隨機(jī)向最大圓內(nèi)拋一粒豆子,則豆子落入圖中陰影部分的概率為( )。

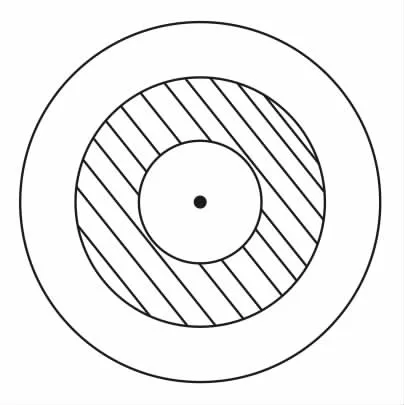
圖1

4.把黑,紅,白3張紙牌分給甲,乙,丙3人,則事件“甲分得紅牌”與事件“乙分得紅牌”是( )。

A.對(duì)立事件

B.互斥但不對(duì)立事件

C.不可能事件

D.必然事件

5.在區(qū)間[-2,3]上任取一個(gè)數(shù)a,則函數(shù)f(x)=x2-2a x+a+2有零點(diǎn)的概率為( )。

A.乙獲勝的概率

B.乙不輸?shù)母怕?/p>

C.甲獲勝的概率

D.甲不輸?shù)母怕?/p>

7.高考數(shù)學(xué)試題中,有12道選擇題,每道選擇題有四個(gè)選項(xiàng),其中只有一個(gè)選項(xiàng)是正確的,則隨機(jī)選擇其中一個(gè)選項(xiàng)正確的概率是,乙獲勝的概率是某家長(zhǎng)說(shuō)：“要是都不會(huì)做,每題都隨機(jī)選擇其中一個(gè)選項(xiàng),則一定有3道題答對(duì)。”這句話( )。

A.正確B.錯(cuò)誤

C.不一定正確D.無(wú)法解釋

8.從{a,b,c,d,e}所有子集中任取一個(gè),這個(gè)集合恰是集合{a,b,c}子集的概率是( )。

9.歐拉是科學(xué)史上一位多產(chǎn)的、杰出的數(shù)學(xué)家。他1707年出生在瑞士的巴塞爾城,淵博的知識(shí),無(wú)窮無(wú)盡的創(chuàng)作精力和空前豐富的著作,都令人驚嘆不已。特別是他頑強(qiáng)的毅力和孜孜不倦的治學(xué)精神,促使他即使在雙目失明以后,也沒(méi)有停止對(duì)數(shù)學(xué)的研究。在失明后的17年間,他還口述了幾本書(shū)和400篇左右的論文。如果你想在歐拉的生日、大學(xué)入學(xué)日、大學(xué)畢業(yè)典禮日、第一篇論文發(fā)表日、逝世日這5個(gè)特別的日子里(這5個(gè)日子均不相同),任選兩天分別舉行班級(jí)數(shù)學(xué)活動(dòng),紀(jì)念這位偉大的數(shù)學(xué)家,則歐拉的生日入選的概率為( )。

10.若x,y∈[-2,2],則x2+y2≤4的概率為( )。

11.從1,2,3,4這4個(gè)數(shù)字中,任取2個(gè)不同的數(shù)字構(gòu)成一個(gè)兩位數(shù),則這個(gè)兩位數(shù)大于30的概率為( )。

12.設(shè)a是從集合{1,2,3,4}中隨機(jī)取出的一個(gè)數(shù),b是從集合{1,2,3}中隨機(jī)取出的一個(gè)數(shù),構(gòu)成一個(gè)基本事件(a,b)。記“這些基本事件中,滿足l o gba≥1”為事件E,則事件E發(fā)生的概率是( )。

13.假設(shè)一個(gè)直角三角形的兩條直角邊的長(zhǎng)都是區(qū)間(0,1)內(nèi)的隨機(jī)數(shù),則斜邊的長(zhǎng)小于的概率為( )。

14.從分別寫(xiě)有A,B,C,D,E的5張卡片中任取2張,這2張卡片上的字母恰好是按字母順序相鄰的概率為( )。

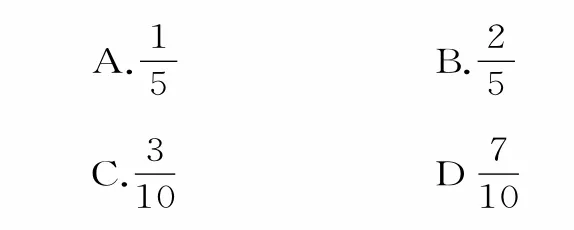
15.在棱長(zhǎng)為2的正方體A B C DA1B1C1D1中,點(diǎn)O為底面A B C D的中心,在正方體A B C D-A1B1C1D1內(nèi)隨機(jī)取一點(diǎn)P,則點(diǎn)P到點(diǎn)O的距離大于1的概率為( )。

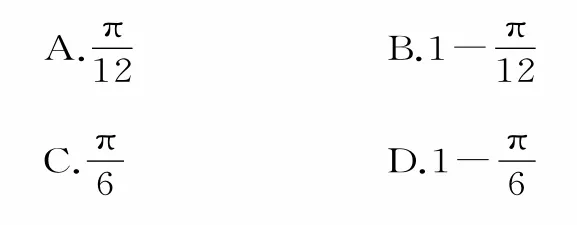
16.甲在微信群中發(fā)布6元“拼手氣”紅包一個(gè),被乙、丙、丁三人搶完。若三人均領(lǐng)到整數(shù)元,且每人至少領(lǐng)到1元,則乙獲得“最佳手氣”(即乙領(lǐng)取的錢(qián)數(shù)不少于其他任何人)的概率是( )。

17.一個(gè)小朋友任意敲擊電腦鍵盤(pán)上的0到9這10個(gè)數(shù)字鍵,則他敲擊兩次(每次只敲擊一個(gè)數(shù)字鍵)得到的兩個(gè)數(shù)字恰好都是3的倍數(shù)的概率為( )。

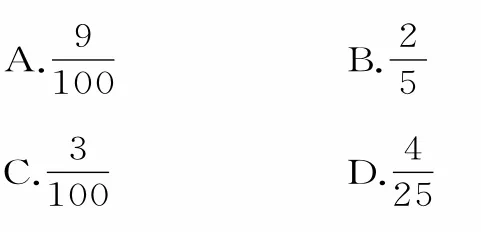
18.從3名男生和2名女生中任選3人參加演講比賽,則這3人中恰有1名男生的概率是( )。

19.《九章算術(shù)》中有如下問(wèn)題：“今有勾八步,股一十五步,問(wèn)勾中容圓,徑幾何。”其大意是：已知直角三角形兩條直角邊長(zhǎng)分別為8步和15步,問(wèn)它的內(nèi)切圓的直徑的大小。現(xiàn)若向此三角形內(nèi)隨機(jī)投一粒豆子,則豆子落在其內(nèi)切圓外的概率是( )。

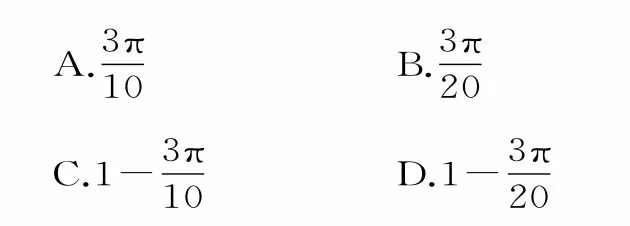
20.甲、乙兩人玩猜數(shù)字游戲,先由甲心中想一個(gè)數(shù)字,記為a,再由乙猜甲剛才所想的數(shù)字,把乙猜的數(shù)字記為b,其中a,b∈{1,2,3,4,5,6},若|a-b|≤1,就稱(chēng)甲乙“心有靈犀”。現(xiàn)任意找兩人玩這個(gè)游戲,則他們“心有靈犀”的概率為( )。

21.表1給出的是三個(gè)游戲規(guī)則,袋子中分別裝有球,從袋子中無(wú)放回地取球,問(wèn)其中不公平的游戲是( )。

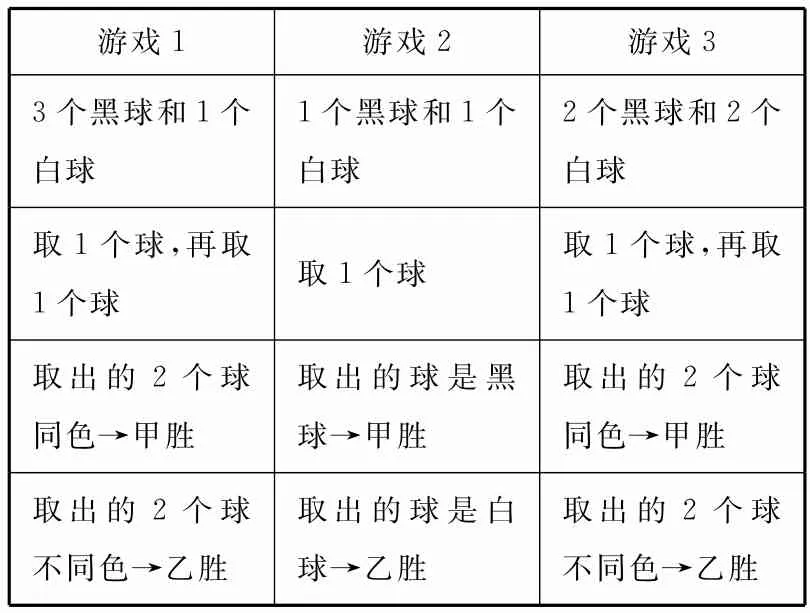
表1

A.游戲1和游戲3

B.游戲1

C.游戲2

D.游戲3

22.已知圓C：x2+y2-2x-2y-10=0,在圓C內(nèi)任取一點(diǎn),則該點(diǎn)到直線l：x+y-的距離不大于2的概率為( )。

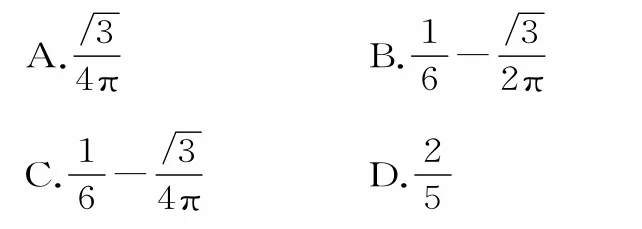
二、填空題

23.小明同學(xué)的QQ密碼是由0,1,2,3,4,5,6,7,8,9這10個(gè)數(shù)字中不同的6個(gè)數(shù)字組成的六位數(shù)碼,由于長(zhǎng)時(shí)間未登錄QQ,小明忘記了密碼的最后一個(gè)數(shù)字,如果小明登錄QQ時(shí)密碼的最后一個(gè)數(shù)字隨意選取,則恰好能登錄的概率是____。

24.在[-4,3]上隨機(jī)取一個(gè)數(shù)m,能使函數(shù)在R上有零點(diǎn)的概率為_(kāi)___。

25.袋中有形狀、大小都相同的4只球,其中1只白球,1只紅球,2只黃球,從中一次隨機(jī)摸出2只球,則這2只球顏色不同的概率為_(kāi)___。

26.在棱長(zhǎng)為2的正方體中隨機(jī)取一點(diǎn),該點(diǎn)落在這個(gè)正方體的內(nèi)切球內(nèi)的概率是____。

27.如圖2,在平行四邊形ABCD中,AB=4,MN=2P Q=2,向該平行四邊形內(nèi)隨機(jī)投一質(zhì)點(diǎn),則該質(zhì)點(diǎn)落在四邊形MNQ P內(nèi)的概率為 。

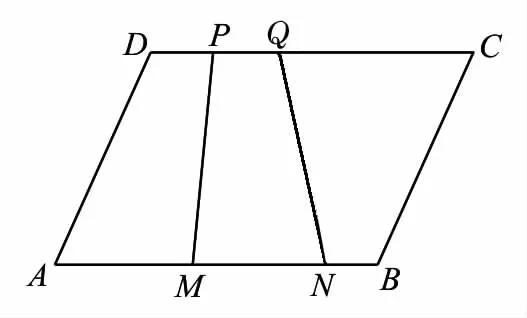
圖2

28.甲,乙,丙這3名同學(xué)上臺(tái)領(lǐng)獎(jiǎng),從左到右按甲,乙,丙的順序排列,則3人全都站錯(cuò)位置的概率是____。

29.“漸升數(shù)”是指每個(gè)數(shù)字比其左邊的數(shù)字大的自然數(shù)(如2578),在兩位的“漸升數(shù)”中任取一數(shù)比37大的概率是____。

30.已知正方形ABCD的邊長(zhǎng)為2,H是邊DA的中點(diǎn)。在正方形ABCD內(nèi)部隨機(jī)取一點(diǎn)P,則滿足?的概率為_(kāi)___。

三、解答題

31.有一個(gè)轉(zhuǎn)盤(pán)游戲,轉(zhuǎn)盤(pán)被平均分成10份(如圖3),轉(zhuǎn)動(dòng)轉(zhuǎn)盤(pán),當(dāng)轉(zhuǎn)盤(pán)停止后,指針指向的數(shù)字即為轉(zhuǎn)出的數(shù)字。游戲規(guī)則如下：兩個(gè)人參加,先確定猜數(shù)方案,甲轉(zhuǎn)動(dòng)轉(zhuǎn)盤(pán),乙猜,若猜出的結(jié)果與轉(zhuǎn)盤(pán)轉(zhuǎn)出的數(shù)字所表示的特征相符,則乙獲勝,否則甲獲勝。

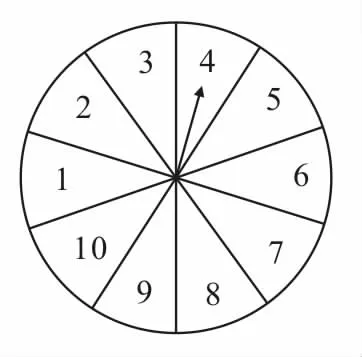
圖3

猜數(shù)方案從以下兩種方案中選一種：

方案A：猜“是奇數(shù)”或“是偶數(shù)”。

方案B：猜“是4的整數(shù)倍”或“不是4的整數(shù)倍”。

請(qǐng)回答下列問(wèn)題：

(1)如果你是乙,為了盡可能獲勝,你會(huì)選哪種猜數(shù)方案?

(2)為了保證游戲的公平性,應(yīng)選哪種猜數(shù)方案?

32.甲,乙,丙三臺(tái)機(jī)床各自獨(dú)立地加工同一種零件,已知甲機(jī)床加工的零件是一等品而乙機(jī)床加工的零件不是一等品的概率為乙機(jī)床加工的零件是一等品而丙機(jī)床加工的零件不是一等品的概率為甲,丙兩臺(tái)機(jī)床加工的零件都是一等品的概率為

(1)求甲,乙,丙三臺(tái)機(jī)床各自加工零件是一等品的概率。

(2)從甲,乙,丙加工的零件中各取一個(gè)檢驗(yàn),求至少有一個(gè)是一等品的概率。

33.某學(xué)校用簡(jiǎn)單隨機(jī)抽樣方法抽取了30名同學(xué),對(duì)其每月平均課外閱讀時(shí)間(單位：h)進(jìn)行調(diào)查,畫(huà)出的莖葉圖如圖4所示。

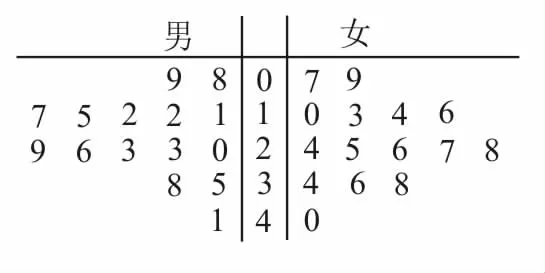
圖4

將月均課外閱讀時(shí)間不低于30h的學(xué)生稱(chēng)為“讀書(shū)迷”。

(1)將頻率視為概率,估計(jì)該校900名學(xué)生中“讀書(shū)迷”有多少人。

(2)從已抽取的7名“讀書(shū)迷”中隨機(jī)抽取男,女“讀書(shū)迷”各1人,參加讀書(shū)日宣傳活動(dòng)。

①共有多少種不同的抽取方法?

②求抽取的男,女2位“讀書(shū)迷”月均讀書(shū)時(shí)間相差不超過(guò)2h的概率。

34.共享單車(chē)是指由企業(yè)在校園、公交站點(diǎn)、商業(yè)區(qū)、公共服務(wù)區(qū)等場(chǎng)所提供的自行車(chē)單車(chē)共享服務(wù),由于其依托“互聯(lián)網(wǎng)+”,符合“低碳出行”的理念,已越來(lái)越多地引起人們的關(guān)注。某部門(mén)為了對(duì)該城市共享單車(chē)加強(qiáng)監(jiān)管,隨機(jī)選取了100人就該城市共享單車(chē)的推行情況進(jìn)行問(wèn)卷調(diào)查,并將問(wèn)卷中的這100人根據(jù)其滿意度評(píng)分值(百分制),按照[50,60),[60,70),…,[90,100]分成5組,制成如圖5所示的頻率分布直方圖。

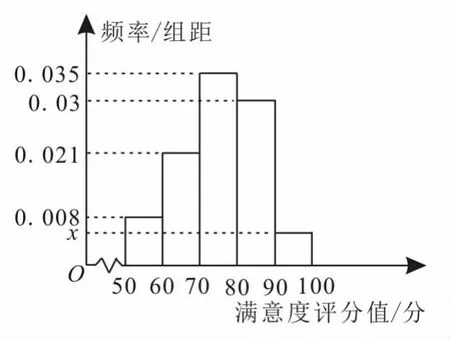
圖5

(1)求直方圖中x的值。

(2)已知滿意度評(píng)分值在[90,100]內(nèi)的男生數(shù)與女生數(shù)的比為2∶1,若在滿意度評(píng)分值在[90,100]內(nèi)的人中隨機(jī)抽取2人進(jìn)行座談,求所抽取的2人中至少有1名女生的概率。

35.已知關(guān)于x的一元二次函數(shù)f(x)=a x2-4b x+1。

(1)已知集合P={1,2,3},Q={-1,1,2,3,4},分別從集合P和Q中隨機(jī)取一個(gè)數(shù)作為a和b,求函數(shù)y=f(x)在區(qū)間[1, +∞)上是增函數(shù)的概率。

(2)設(shè)點(diǎn)(a,b)是區(qū)域的隨機(jī)點(diǎn),求函數(shù)y=f(x)在區(qū)間[1,+∞)上是增函數(shù)的概率。