概率與統計創新問題賞析

■楊 虎

概率與統計是新課標內容中的一個重要知識點,概率與統計也是新課改后逐步登上高考舞臺的“新生花旦”。不難發現概率與統計試題一般是在生活化的問題情境中,考查同學們分析數據、提取信息、解決實際問題的應用能力。高考數學試題越來越注重問題情境的設置,通過一些貼近生活、緊扣熱點、反映潮流的新穎素材來體現概率與統計的應用價值,以期達到解決現實中的具體問題之目的。下面列舉近幾年高考數學試卷中的概率與統計試題進行歸類賞析。

一、概率與區域面積牽手

例1如圖1,設拋物線y=-x2+1的頂點為A,與x軸正半軸的交點為B,拋物線與兩坐標軸正半軸圍成的區域為M,且區域M的面積為,隨機往區域M內投一點P,則點P落在△A O B內的概率是( )。

圖1

解：由題設可得拋物線y=-x2+1與x軸正半軸及y軸的正半軸所圍成的區域面積為,容易得到

設事件N=“隨機往區域M內投一點P,則點P落在△A O B內”,故所求概率為

利用函數為命題背景考查概率知識是本題的一大亮點。近幾年高考在對概率的考查上重視命題背景,突出了概率與其他知識的交匯。

二、概率與體育競賽同行

例 2某校在一次趣味運動會的頒獎儀式上,高一、高二、高三各代表隊人數分別為120、120、n。為了活躍氣氛,大會組委會在頒獎過程中穿插抽獎活動,并用分層抽樣的方法從三個代表隊中共抽取20人在前排就座,其中高二代表隊有6人。

(1)求n的值。

(2)把在前排就座的高二代表隊的6人分別記為a,b,c,d,e,f,現隨機從中抽取2人上臺抽獎,求a和b至少有1人上臺抽獎的概率。

(3)抽獎活動的規則是：代表通過操作按鍵使電腦自動產生兩個[0,1]之間的均勻隨機數x,y,并按如圖2所示的程序框圖執行。若電腦顯示“中獎”,則該代表中獎;若電腦顯示“謝謝”,則該代表不中獎。求該代表中獎的概率。

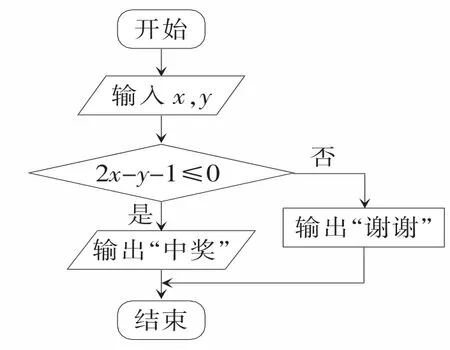
圖2

解：(1)根據分層抽樣的特點可得解得n=160。

(2)高二代表隊的6人分別記為a,b,c,d,e,f,從中抽取2人上臺抽獎的基本事件為(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15種情況,其中a和b至少有1人上臺抽獎的基本事件為(a,b),(a,c),(a,d),(a,e),(a,f),(b,c), (b,d),(b,e),(b,f),共9種情況。

故a和b至少有1人上臺抽獎的概率為

(3)已知0≤x≤1,0≤y≤1,點(x,y)在如圖3所示的邊長為1的正方形O A B C內。根據程序框圖和已知條件可知滿足,的區域為如圖3所示的陰影部分。

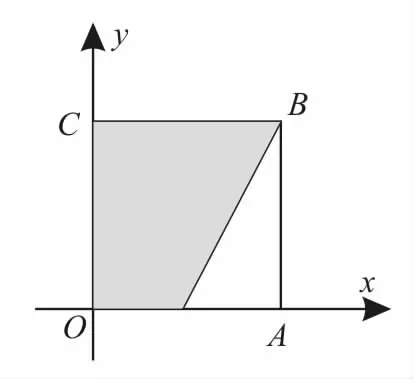
圖3

根據2x-y-1=0,令y=0可得x=,令y=1可得x=1。當x,y∈[0,1]時,可知滿足2x-y-1≤0的區域面積為S=

本題將抽獎與概率結合,讓試題增加了趣味性,而抽獎活動在生活中比比皆是,以抽獎為背景命題,這體現了數學知識與實際生活的密切聯系。

三、概率與新概念結合

例 3全網傳播的融合指數是衡量電視媒體在中國網民中影響力的綜合指標。根據相關報道提供的全網傳播2016年某全國性大型活動的“省級衛視新聞臺”融合指數的數據,對名列前20名的“省級衛視新聞臺”的融合指數進行分組統計,結果如表1所示。

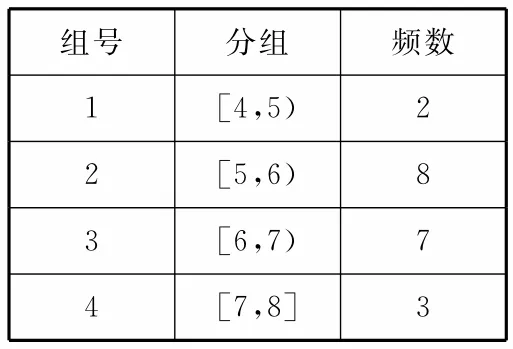
表1

(1)現從融合指數在[4,5)和[7,8]內的“省級衛視新聞臺”中隨機抽取2家進行調研,求至少有1家的融合指數在[7,8]內的概率。

(2)根據分組統計表求這20家“省級衛視新聞臺”的融合指數的平均數。

解：(1)(方法1)融合指數在[7,8]內的“省級衛視新聞臺”記為A1,A2,A3;融合指數在[4,5)內的“省級衛視新聞臺”記為B1,B2。從融合指數在[4,5)和[7,8]內的“省級衛視新聞臺”中隨機抽取2家的所有基本事件為{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10種情況。

其中至少有1家融合指數在[7,8]內的基本事件為{A1,A2},{A1,A3},{A2,A3}, {A1,B1},{A1,B2},{A2,B1},{A2,B2}, {A3,B1},{A3,B2},共9種情況。

(方法2)融合指數在[7,8]內的“省級衛視新聞臺”記為A1,A2,A3;融合指數在[4,5)內的“省級衛視新聞臺”記為B1,B2。從融合指數在[4,5)和[7,8]內的“省級衛視新聞臺”中隨機抽取2家的所有基本事件為{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10種情況。

其中沒有1家融合指數在[7,8]內的基本事件為{B1,B2},共1種情況。

(2)由表1中數據可知,這20家“省級衛視新聞臺”的融合指數的平均數為

融合指數是新聞專業里的“術語”,全網傳播的融合指數是衡量電視媒體在中國網民中影響力的綜合指標。越來越注重數學與生活的聯系是高考命題的方向之一,本題命題背景體現了關注生活也就是關注數學的理念。

例4某次測量發現一組數據(xi,yi)具有較強的相關性,并計算可得^y=x+1,其中數據(1,y0)因書寫不清,只記得y0是[0,3]內的任意值,則該數據對應的殘差的絕對值不大于1的概率為____。(殘差=真實值-預測值)

：由=x+1,得=1+1=2,可知預測值為2。利用該數據對應的殘差的絕對值不大于1,可得|y0-2|≤1,解得1≤y0≤3,即y0∈[1,3]。

由于y0是[0,3]內的任意值,因此該數據對應的殘差的絕對值不大于1的概率為

新概念題目比較注重對同學們閱讀理解能力的考查,所以平時對閱讀理解型題目的學習與積累是非常必要的。

四、概率與直線和圓的交匯

例5在[-1,1]上隨機地取一個數k,則事件“直線y=k x與圓(x-5)2+y2=9相交”發生的概率為____。

解：直線y=k x與圓(x-5)2+y2=9相交,需滿足圓心到直線的距離小于或等于半徑,即而k∈[-1,1],故所求概率

本題的綜合應用性較強,具有“無圖考圖”的顯著特點。在直線和圓的知識與概率知識的交匯處命題,充分考查了同學們分析問題、解決問題的綜合能力。

五、概率與實際應用牽手

例6某超市隨機選取1000名顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成統計表,如表2所示,其中“√”表示購買,“×”表示未購買。

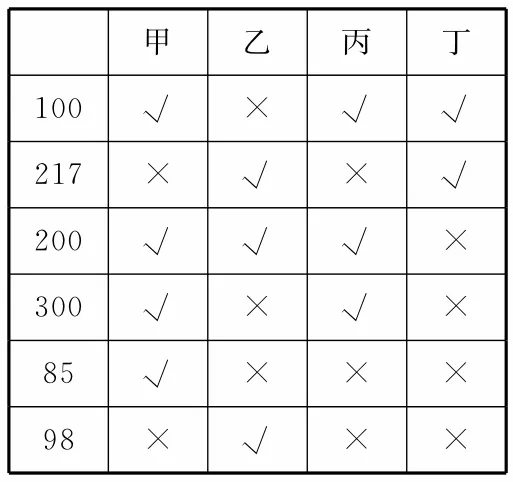
表2

(1)估計顧客同時購買乙和丙的概率。(2)估計顧客在甲、乙、丙、丁四種商品中同時購買三種商品的概率。

(3)如果顧客購買了甲,則該顧客同時購買乙、丙、丁中那種商品的可能性最大?

解：(1)從統計表中可以看出,在這1000名顧客中,有200名顧客同時購買了乙和丙,所以顧客同時購買乙和丙的概率的估計值為

(2)從統計表中可以看出,在這1000名顧客中,有100名顧客同時購買了甲、丙、丁,另有200名顧客同時購買了甲、乙、丙,其他顧客最多購買了兩種商品。所以顧客在甲、乙、丙、丁四種商品中同時購買三種商品的概率的估計值為

(3)根據統計表可知,顧客同時購買甲和乙的概率的估計值為

由上可知,如果顧客購買了甲,則該顧客同時購買丙的可能性最大。

本題主要考查統計與概率的基礎知識,考查同學們分析問題和解決問題的能力。