概率問題的新考向

概率知識是新課標高中數學的重點內容。下面例析概率問題的新考向,供大家學習與參考。

新考向1：程序框圖

例1在可行域內任取一點,規則如圖1所示的流程圖,則能輸出數對(x,y)的概率為( )。

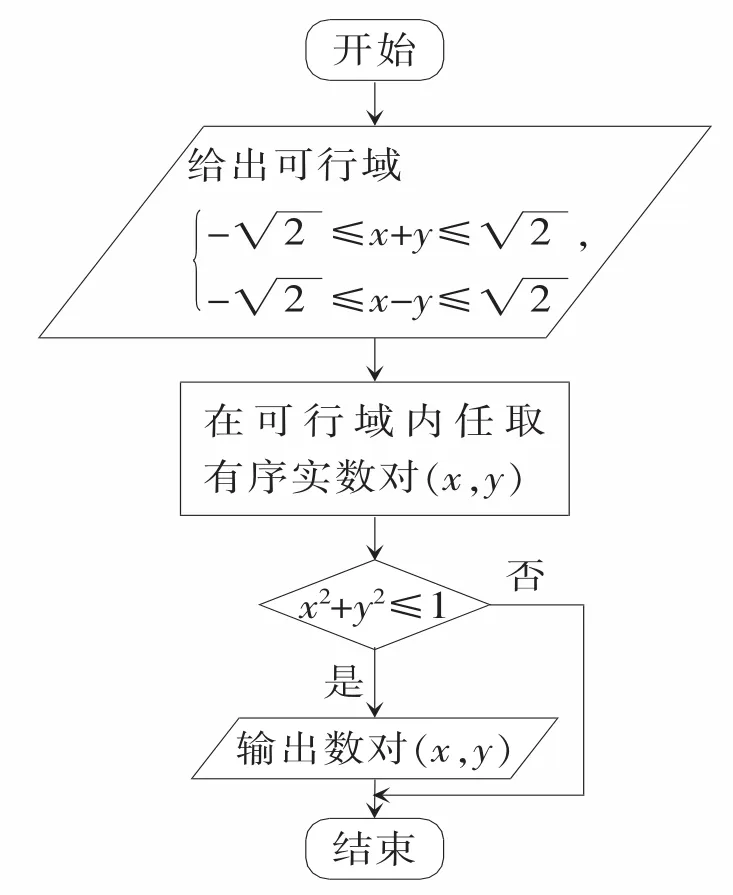
圖1

解：閱讀程序框圖,由程序框圖可知不等式組表示的平面區域如圖2所示,其面積為滿足不等式x2+y2≤1的點表示的區域為圖2所示的正方形的內切圓,其面積為π。

圖2

故由幾何概型可知能輸出數對(x,y)的概率為應選C。

程序框圖的輸入框只是表示一個算法輸入的信息,而處理框主要是賦值、計算。利用條件結構解決算法問題時,關鍵要分析判斷框,判斷框內的條件不同,對應下一步的內容和操作都要相應地進行變化。

新考向2：頻率分布直方圖

例22017年下學期某市教育局對某校高三文科數學進行教學調研,從該校文科生中隨機抽取40名學生的數學成績進行統計,將他們的成績分成6段：[80,90),[90,100), [100,110),[110,120),[120,130),[130, 140]后得到如圖3所示的頻率分布直方圖。

圖3

(1)求這40個學生數學成績的眾數和中位數的估計值。

(2)若從數學成績在[80,100)內的學生中任意抽取2人,求成績在[80,90)內至少有1人的概率。

解：(1)眾數的估計值為最高矩形對應的成績區間的中點,即得眾數的估計值為115。

設中位數的估計值為x,易知中位數在第4個小長方形內,則10×0.005+0.01× 10+0.02×10+(x-110)×0.03=0.5,解得x=115,所以中位數的估計值為115。

(2)從圖中可知,成績在[80,90)內的人數為m1=0.005×10×40=2,成績在[90, 100)內的人數為m2=0.01×10×40=4。

設成績在[80,90)內的學生記為a,b,成績在[90,100)內的學生記為c,d,e,f,則從成績在[80,100)內的學生中任取2人組成的基本事件為(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e), (b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15種,其中成績在[80,90)內的學生至少有1人的基本事件為(a,b), (a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),共9種。

在頻率分布直方圖中,中位數左邊和右邊的小長方形的面積之和是相等的。

新考向3：莖葉圖

例3甲、乙兩組數據的莖葉圖如圖4所示,其中m為小于10的自然數,已知甲組數據的中位數大于乙組數據的中位數,則甲組數據的平均數大于乙組數據的平均數的概率為____。

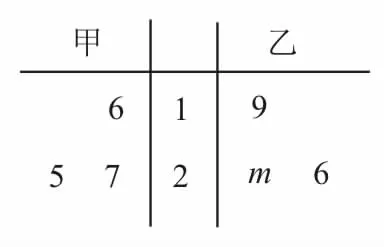
圖4

解：由莖葉圖可知,甲組數據的中位數為25,平均數為

用莖葉圖表示數據有兩個優點：一是沒有原始數據信息的損失,所有數據信息都可以從莖葉圖中得到;二是莖葉圖中的數據可以隨時記錄,隨時添加,方便記錄與表示。

新考向4：獨特民俗登高節

例 4正月十六登高是“中國石刻藝術之鄉”、“中國民間文化藝術之鄉”四川省巴中市沿襲千年的獨特民俗。登高節前夕,李大伯在家門前的樹上掛了兩串喜慶彩燈,這兩串彩燈的第一次閃亮相互獨立,且都在通電后4 s內的任一時刻等可能發生,然后每串彩燈以4s為間隔閃亮。那么這兩串彩燈同時通電后,它們第一次閃亮的時刻相差不超過2 s的概率是____。

解：設兩串彩燈第一次閃亮的時刻分別為x,y,則全部基本事件構成的區域為而符合題意的事件構成的區域為即如圖5所示的陰影部分。

圖5

解答本題的主要步驟是：列出條件組,畫出圖形,計算面積,利用對立事件,求其概率。

新考向5：三角函數

例5已知函數f(x)=s i nx+,當x∈[0,π]時,f(x)≥1的概率為( )。

解：由函數,再利用三角函數的圖像與性質可得到

根據幾何概型的概率計算公式可得滿足f(x)≥1的概率為應選D。

解答測度為長度的幾何概型問題,只要將所有基本事件及事件A包含的基本事件轉化為相應長度,即可利用幾何概型的概率計算公式求解。此處的“長度”可以是區間的長短,也可以是時間的長短等。

新考向6：訂購酸奶

例6某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完。根據往年銷售經驗,每天需求量與當天最高氣溫(單位：℃)有關。如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間[20,25),需求量為300瓶;如果最高氣溫低于20,需求量為200瓶。為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得到的頻數分布表,如表1所示。(以最高氣溫位于各區間的頻率代替最高氣溫位于該區間的概率)

表1

(1)求六月份這種酸奶一天的需求量不超過300瓶的概率。

(2)設六月份一天銷售這種酸奶的利潤為Y(單位：元),當六月份這種酸奶一天的進貨量為450瓶時,寫出Y的所有可能值,并估計Y＞0的概率。

解：(1)設“六月份這種酸奶一天的需求量不超過300瓶”為事件A。

由題意可知,所求概率P(A)=(2)由題意可知,當最高氣溫不低于25

時,Y=(6-4)×450=900,其概率P=

當最高氣溫位于區間[20,25)時,Y= (6-4)×300-(4-2)×(450-300)=300,其概率

當最高氣溫低于20時,Y=(6-4)×200-(4-2)×(450-200)=-100,其概率

綜上可知,Y的所有可能取值為900,300和-100;Y＞0的概率為

本題的易錯點是遺漏“不超過”的情況,從而產生錯解。