QC新七大工具之一：箭線圖法

◆王為人

箭線圖法又稱矢線圖法或雙代號網絡圖法(Activity-On-Arrow，AOA)，是計劃評審法在質量管理中的具體運用。它有4個要素：(1)節點。表示工作之間的聯結，不占用任何時間和資源，僅表示指向節點的工作全部完成后，該節點后面的工作才能開始。也稱為事件。(2)工作。 在箭線圖中，工作是一個廣義的概念，一項工作是指一個相對獨立的具體活動過程，往往需要消耗一定資源和時間。也稱活動。(3)虛工作(邏輯箭線)。 虛工作是一項虛擬的工作，僅為了準確清楚地表示工作間的邏輯關系，無工作名稱，既不消耗時間，也不消耗資源。用虛箭線表示，其持續時間為0。如用實箭線表示，需標注持續時間為0。(4)路線。 從箭線圖的起始節點出發，沿箭線方向，經過一系列節點和箭線，至箭線圖終止節點所經過的通道。

箭線圖法有利于從全局出發，統籌安排，抓住關鍵線路，集中力量，按時或提前完成計劃。一般而言，箭線圖法可應用于以下5方面：(1)項目計劃制定及管理；(2)新產品或服務開發進程的規劃和改善；(3)試驗階段計劃的制定及管理；(4)交付期管理；(5)較復雜活動的籌辦及計劃管理等。

箭線圖法邏輯關系及規則

根據箭線圖中相關工作之間的邏輯關系，可以將工作劃分為：(1) 緊前工作。指緊接在該工作之前的工作。緊前工作不結束，則該工作不能開始；(2)緊后工作。指緊接在該工作之后的工作。該工作不結束，緊后工作不能開始；(3)平等工作。指能與該工作同時開始的工作；(4)交叉工作。指能與該工作相互交替進行的工作。

繪制箭線圖時必須注意節點與箭線的下列關系：進入某一節點的各項工作必須全部完成，該節點所表示的事件才能出現；某一節點出現后，由該節點引出的各項工作才能開始。兩個節點之間只能有一項工作。當兩個節點間有兩項或以上可以平行進行的工作時，其他一項或幾項則用虛箭線表示的虛擬工作來連接，說明此兩節點間存在的邏輯關系。箭線圖中工作之間的邏輯關系是相對的，只有指定了某一確定工作，考察與之有關各項工作的邏輯聯系，才是有意義的。

繪制箭線圖有以下規則：(1)只能有一個起始節點和一個終止節點；(2)箭線首尾必須有節點；(3)不允許出現循環路線；(4)相鄰網絡節點間只能有一條箭線；(5)節點編號的正確標注；(6)正確反映工作間的邏輯關系；(7)正確表示平行、交叉工作；(8)避免出現“橋路”，即箭線圖中出現的箭線與箭線的交叉。

箭線圖的繪制

(1)確定目標和約束條件。確定應達成的目標(例如應完成的項目與工期)以及醫院所具備的資源、環境等約束條件。

(2)項目分解。將整個項目用系統方法逐層分解，直到可以實施管理的子項目，即單個工作為止。

(3)編制工作一覽表。根據項目分解得出的工作，編制工作一覽表，并估計每一工作的工期。

(4)確定工作順序。按照技術要求和資源條件(人力、設備、物資等)許可，確定各個工作之間的先后關系。

(5)繪制箭線圖。根據工作一覽表和工作順序，繪制箭線圖。對于簡單的小型項目，繪制一張總圖即可；對于大型復雜項目，可以先按子系統分別繪制，然后銜接而成總圖。

(6)在實施過程中進行分析和調整。

箭線圖繪制具體步驟

(1) 調查工作項目，按先后次序編號。

(2) 用箭條→代表某項工作過程，如0→1、1→2等。箭條上方可標出該項工作所需時間數，工作時間單位常以日或周表示。

(3)各項工作過程的時間的確定可用經驗估計法求出。這種經驗估計法公式基于Beta分布，又稱三點估計法。工作時間按3種情況進行估計：①樂觀估計時間，用a表示；②悲觀估計時間，用b表示；③最有可能時間，用m表示。經驗估計工作時間T，也稱期望時間:

工作時間標準差σ:

建議記住這3個典型的概率：工作時間落在1個標準差范圍之內的概率是68.26%，2個標準差之內的概率是95.46%，3個標準差之內的概率是99.73%，如果用1個標準差來估算工作時間，那工期在(T+σ)的范圍內完成的概率是68.26%。例如，對某一工作過程的時間估計a為2天，b為9天，m為4天，用三點估計法求得的期望工作時間 T為4.5天，標準差σ為1.17天，即5.7天完成工作的概率為68.26%，6.9天完成工作的概率是95.46%，8.0天完成工作的概率是99.73%。

即使脫離箭線圖范疇，三點時間估計法的應用范圍也是非常廣泛的，可以用于醫院的許多環節，如救護車到達時間、手術時間、治療時間等。

(4)繪制箭線圖。有兩種方法：①順推法。按照工作順序從前往后繪制箭線圖。②逆推法。首先觀察哪些工作不是其他工作緊前工作，它們必須與網絡終點連結。找出這些工作的緊前工作，再依次往前推，直至到最早的再也沒有緊前工作的所有工作，它們必須與網絡起點連結。

(5)計算每個節點上的最早開工時間。某節點上的最早開工時間是指從始點開始順箭頭方向到該節點的各條路線中，時間最長一條路線的時間之和。

(6)計算每個節點上的最晚開工時間。某節點上的最晚開工時間是指從終點逆箭頭方向到該節點的各條路線中，時間差最小的時間。

(7)計算富余時間，找出關鍵線路。富余時間是指在同一節點上最早開工時間與最晚開工時間之間的時差。有富余時間的節點，對工程進度影響不大，屬于非關鍵工作。無富余時間或富余時間最少的節點，是關鍵工作。把所有關鍵工作按照工藝流程順序連接起來，就是這項工程的關鍵線路。

案例分析

假設某醫院進行的新項目的初始箭線圖計劃如圖1所示。圖中箭線上方字母代表工作名稱，括號外數字為工作按正常持續時間完成所需直接費用，括號內數字為工作按最短持續時間完成所需直接費用；箭線下方括號外數字為工作正常持續時間，括號內數字為最短持續時間。該工程間接費用率為0.9萬元/天。嘗試對本工程造價進行優化。

(1)根據各項工作的正常持續時間，確定初始項目計劃的計算工期和關鍵線路。初始項目計劃的關鍵線路有兩條：B-E-G-I和B-E-H。計算工期為20天，正常持續時間項目直接費用為68.5萬元，間接費用為18萬元，總費用為86.5萬元。

(2)計算各項工作時間壓縮的費用率。F_a=0.3萬元/天，F_b=1.0萬元/天，F_c=0.6萬元/天，F_d=1萬元/天，F_e=0.1萬元/天，F_f=0.8萬元/天，F_g=0.7萬元/天，F_h=0.5萬元/天，F_i=0.2萬元/天。

(3)費用優化。如果壓縮關鍵線路上的工作持續時間，使工期縮短，可以降低間接費用，從而降低總費用。

①第一次壓縮。因為在圖1上的初始網絡計劃有兩條關鍵線路，為了同時縮短兩條關鍵線路上的總時間，有4個壓縮方案：壓縮工作B，直接費用率為1.0萬元/天；壓縮工作E，直接費用率為0.1萬元/天；同時壓縮工作H和G，兩項直接費用率為1.2萬元/天；同時壓縮工作H和I，兩項直接費用率為0.7萬元/天。在這4個壓縮方案中，工作E的直接費用率最低，且小于間接費用率0.9萬元/天，說明壓縮工作E可使總費用降低。將工作E持續時間壓縮為3天，并重新確定計算工期和關鍵線路。此時，關鍵線路為B-F-I，關鍵工作E被壓縮成非關鍵工作，如果只將E工作時間壓縮1天，即其工作持續時間延長至4天，也使其成為關鍵工作。此時關鍵線路變成3條：B-E-H、B-E-G-I和B-F-I。

②第二次壓縮。有以下5個方案：壓縮工作B，直接費用率為1.0萬元/天；同時壓縮工作E和F，兩項直接費用率為0.9萬元/天；同時壓縮工作E和I，兩項直接費用率為0.3萬元/天；同時壓縮工作F、G和H，三項直接費用率為2.0萬元/天；同時壓縮工作H和I，兩項直接費用率為0.7萬元/天。上述壓縮方案中，由于工作E和I的組合費用率最低，且低于間接費用率0.9萬元/天，說明同時壓縮工作E和I可使總費用降低。由于工作E只能壓縮1天，工作I的持續時間也只能隨之壓縮1天，工作E和I的持續時間同時壓縮1天后，關鍵線路由壓縮前的3條變為2條，即B-E-H、B-F-I。

③第三次壓縮。有以下3個方案：壓縮工作B，直接費用率為1.0萬元/天；同時壓縮工作F和H，兩項直接費用率為1.3萬元/天；同時壓縮工作H和I，兩項直接費用率為0.7萬元/天。上述壓縮方案中，由于工作H和I的組合費用率最低，且低于間接費用率0.9萬元/天，說明同時壓縮工作H和I可使總費用降低。由于工作I只能壓縮1天，工作H的持續時間也只能隨之壓縮1天，工作I和H的持續時間同時壓縮1天后，關鍵線路仍為B-E-H、B-F-I。

④第四次壓縮。有以下兩個方案：壓縮工作B，直接費用率為1.0萬元/天；同時壓縮工作F和H，兩項直接費用率為1.3萬元/天。上述壓縮方案中，由于兩個方案的壓縮費用率均大于間接費用率0.9萬元/天，說明不管選擇哪個壓縮方案均使總費用增加。因此，不需要壓縮工作，此方案已為最優方案。此時，計算工期為17天。最后，得到優化后的箭線圖如圖2所示。

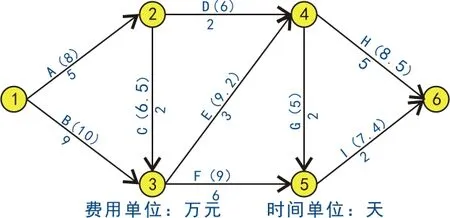
圖2　優化后的箭線圖

(4)計算方案優化后的項目總費用。直接費用為69.6萬元，間接費用為15.3萬元，總費用為84.9萬元。經過優化，該項目總費用減少1.6萬元，工期縮短3天。