基于信號燈狀態(tài)的燃油最優(yōu)車速規(guī)劃與控制
張博 郭戈 王麗媛 王瓊
近年來,城市道路車輛數(shù)量迅速增加,能源消耗和環(huán)境污染問題日趨嚴(yán)重,如何緩解交通壓力,減少汽車油耗及尾氣排放已成為亟待解決的重要問題[1].車輛油耗不僅受發(fā)動機(jī)性能、路況及天氣影響,行駛過程的速度控制也直接決定著油耗的多少.燃油高效的車輛行駛控制方法已成為智能交通系統(tǒng)(Intelligent transport systems,ITSs)領(lǐng)域的研究熱點(diǎn)之一,受到學(xué)術(shù)界和汽車制造商的極大關(guān)注.
僅2014年我國汽車銷量為2349.19萬輛,其中乘用車銷量為1970.06萬輛,新能源汽車銷售量為74.763萬輛[2],由此可見傳統(tǒng)燃油乘用車仍然是汽車行業(yè)的中流砥柱.本文關(guān)注對家庭普通燃油乘用車的能耗和駕駛特性的研究和分析.經(jīng)過長期的發(fā)展,ITS在諸多方面已取得顯著進(jìn)展,例如,利用通信和傳感技術(shù)的避碰系統(tǒng)[3]、可自動調(diào)節(jié)速度保持安全車距的自適應(yīng)巡航控制[4]、更注重燃油效率的合作自適應(yīng)巡航控制[5]等.上述技術(shù)的發(fā)展和應(yīng)用擴(kuò)大了路容,增強(qiáng)了交通安全[6],也在一定程度上提高了燃油利用率.近年來,傳感器技術(shù)和智慧道路的推廣應(yīng)用促生了先進(jìn)駕駛輔助系統(tǒng)(Advanced driver assistant systems,ADAS),它幫助駕駛員對路況和交通狀況做出更準(zhǔn)確及時的判斷,從而進(jìn)一步降低車輛油耗[7].隨著人們環(huán)保意識的增強(qiáng),利用交通信息降低燃油消耗的環(huán)保駕駛技術(shù)日益受到關(guān)注[8].環(huán)保駕駛策略可根據(jù)復(fù)雜多變的交通環(huán)境,給駕駛員提供油耗最優(yōu)的車輛駕駛方案[9].早期的環(huán)保駕駛策略只給出“加速”和“減速”等簡單操縱建議,如文獻(xiàn)[10]提出的駕駛輔助系統(tǒng)可基于道路及駕駛習(xí)慣等信息為駕駛員提供合理的駕駛建議.實(shí)驗表明,利用環(huán)保駕駛技術(shù)可減少10%~15%的油耗和20%的空氣污染[11].文獻(xiàn)[12]考慮行車時間和效率要求,提出一種兼顧油耗和行車時間的環(huán)保駕駛輔助系統(tǒng)策略,避免了以犧牲行車時效來降低油耗,實(shí)現(xiàn)油耗與時間的平衡.文獻(xiàn)[13?14]將油耗優(yōu)化問題轉(zhuǎn)化為最優(yōu)速度控制問題,通過動態(tài)規(guī)劃方法獲得燃油最優(yōu)的行車路徑.文獻(xiàn)[15]根據(jù)駕駛行為分析提出一種更為環(huán)保的改進(jìn)動態(tài)規(guī)劃方法.另外,基于交通環(huán)境預(yù)測降低油耗的環(huán)保駕駛技術(shù)也受到普遍關(guān)注[16],比如,文獻(xiàn)[9]考慮道路坡度對汽車油耗的影響,提出一種基于路況信息預(yù)測的環(huán)保駕駛策略,文獻(xiàn)[17?18]通過預(yù)測前車加速度和速度來調(diào)節(jié)車輛速度,從而減少油耗.
在城市道路中,信號燈狀態(tài)對車輛油耗起著至關(guān)重要的影響.如果車輛行駛中能利用前方交通信號燈狀態(tài)及切換周期,則可避免紅燈前的空轉(zhuǎn)和頻繁啟/停操作造成的額外油耗.這樣的環(huán)保駕駛技術(shù)可更好地適應(yīng)城市交通環(huán)境.車–車(V2V)及車–路(V2I)通信技術(shù)[19]使得車輛行駛中獲取前方信號燈信息成為可能.最近已出現(xiàn)基于信號燈的車輛速度和軌跡規(guī)劃方面的研究成果,文獻(xiàn)[20?21]基于信號燈狀態(tài)提出可使車輛連續(xù)通過盡可能多綠燈的一種智能駕駛策略,從而降低油耗;文獻(xiàn)[22]采用局部最優(yōu)化的方法,在降低油耗的同時保證給定的行車時間要求.上述方法都是通過保持穩(wěn)定的速度而間接實(shí)現(xiàn)節(jié)能目標(biāo)的,忽略了車輛駛往目的地過程中的速度變化,控制器設(shè)計的重點(diǎn)在于提高速度跟蹤性能.事實(shí)上,降低車輛油耗的關(guān)鍵是盡可能減少剎車頻率,保證車輛盡量以恒定速度行駛,且避免過大的加速度[18].可見,已有成果并未充分考慮信號燈狀態(tài)及其切換周期,以及車輛加減速和頻繁起停對油耗的影響.
本文提出一種基于信號燈狀態(tài)及切換周期信息的燃油最優(yōu)行駛控制方法.結(jié)合信號燈以及當(dāng)前交通狀態(tài),基于車輛速度、加速度以及與信號燈的距離,獲得車輛在信號燈路段的最優(yōu)速度規(guī)劃.以此速度為實(shí)際行駛時的參考速度,基于車輛縱向運(yùn)動的動力學(xué)模型以及綜合速度跟蹤誤差和油耗指標(biāo),提出可保證燃油最優(yōu)的車輛行駛速度模型預(yù)測控制方法(Model predictive control,MPC).本文主要創(chuàng)新點(diǎn)如下:
1)在基于信號燈的速度規(guī)劃部分,制定了細(xì)致嚴(yán)謹(jǐn)?shù)乃俣惹袚Q規(guī)則,獲得免停車平穩(wěn)通過信號燈的最佳速度規(guī)劃.
2)同時考慮了信號燈狀態(tài)及周期信息、速度跟蹤誤差及車輛油耗,獲得最優(yōu)車輛行駛控制策略.
3)性能指標(biāo)中的參考速度根據(jù)信號燈狀態(tài)實(shí)時動態(tài)規(guī)劃,有利于實(shí)際城市交通應(yīng)用.
本文結(jié)構(gòu)如下:第1節(jié)建立了車輛動態(tài)模型,提出油耗模型及性能指標(biāo);第2節(jié)基于信號燈信息預(yù)測,給出車輛免停車且平穩(wěn)通過綠燈的速度規(guī)劃,以及實(shí)現(xiàn)該目標(biāo)速度的MPC控制方法;第3節(jié)是仿真實(shí)驗驗證與分析;第4節(jié)為本文結(jié)論.
1 問題描述及目標(biāo)
1.1 車輛建模
根據(jù)牛頓第二定律,建立車輛縱向動力學(xué)模型[23]:
其中,[p,v,a]分別是車輛的位置、速度和加速度,F是車輛的驅(qū)動力,其大小與車輛加速度有關(guān),ρ是空氣密度,A是車輛橫截面積,Cd是空氣阻力系數(shù),cr是滾動摩擦系數(shù),θ(p)是道路坡度角.本文考慮在城市道路環(huán)境中的車輛縱向駕駛情況,所以θ通常很小,可以近似表示為:cos(θ(p))≈1,sin(θ(p))≈θ(p).g是重力加速度,m是車的質(zhì)量.
另外,由文獻(xiàn)[24]可知,車輛的發(fā)動機(jī)模型如下:
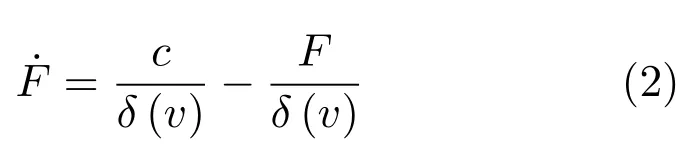
其中,δ是發(fā)動機(jī)的時間常數(shù),c是車輛的節(jié)氣閥輸入量.由式(1)和式(2)得到:
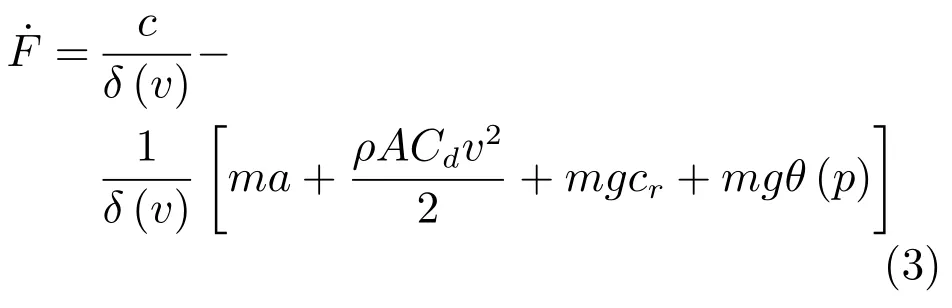
對式(1)關(guān)于加速度a求導(dǎo)后,得到關(guān)系式:m˙a=˙F?ρACdva,將其代入式(3)得:
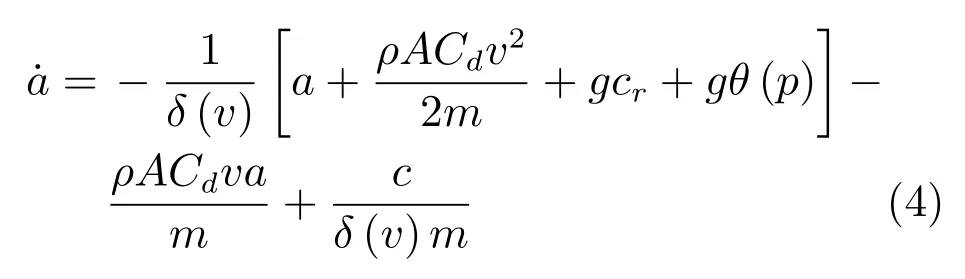
引入如下反饋線性化控制器:c=,其中u為引入的控制輸入,其與加速度大小相關(guān),于是可將車輛動態(tài)特性描述為如下狀態(tài)空間方程:
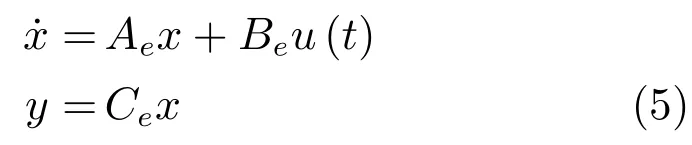
其中,狀態(tài)向量x=[p,v,a]T,u為車輛的控制輸入,
1.2 油耗模型
隨后建立車輛的油耗模型,車輛的油耗與發(fā)動機(jī)的轉(zhuǎn)矩、傳動比、溫度等因素有關(guān),實(shí)際的油耗方程十分的繁瑣復(fù)雜.本文以每千瓦時能量輸出的燃油量來評價發(fā)動機(jī)燃油經(jīng)濟(jì)性,采用如下油耗模型,得到近似油耗方程[18]:
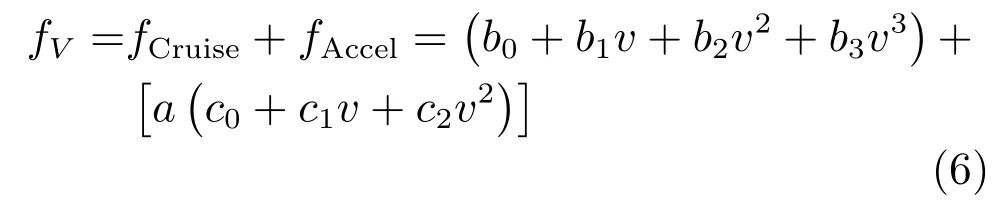
其中,fCruise表示在穩(wěn)定速度v下每秒的巡航油耗,fAccel表示在速度v時加速度的存在所產(chǎn)生的加速油耗.
1.3 控制目標(biāo)
本文的目標(biāo)是設(shè)計外部控制輸入u,使下述油耗及誤差指標(biāo)達(dá)到最優(yōu):
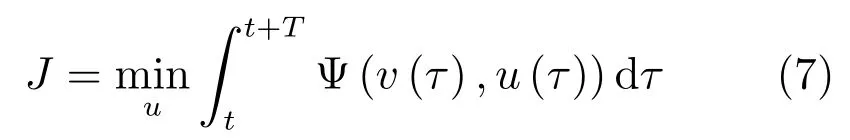
其中函數(shù)Ψ定義為
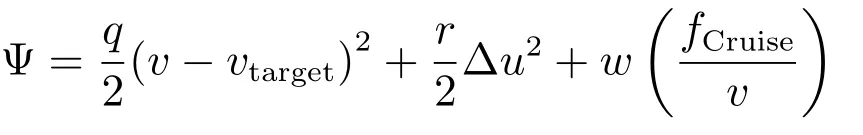
其中,q、r和w為權(quán)重系數(shù),vtarget是根據(jù)信號燈信息得到的參考速度.為了確保車輛能夠在單位油耗下盡可能勻速駕駛最大的距離,在性能指標(biāo)中,我們選取巡航時的油耗fCruise而不是整體油耗[17],這樣就可以減少加速度的產(chǎn)生和變化,使得車輛盡可能以恒定速度維持勻速駕駛.
2 基于信號燈預(yù)測的車速規(guī)劃與優(yōu)化控制
2.1 基于信號燈信息的速度規(guī)劃
假設(shè)車輛與信號燈之間可以通過專用短距離無線通信技術(shù)進(jìn)行通信[25],本節(jié)的目的是基于車輛獲得的信號燈狀態(tài)、相位和時間等信息,為車輛規(guī)劃油耗最優(yōu)的行車速度.這一過程須遵循如下規(guī)則[26]:
a)應(yīng)盡可能避免頻繁加速/減速操作;
b)應(yīng)避免急剎車/急加速情況;
c)應(yīng)盡量減少紅燈前停車等待,保證綠燈時通過信號燈;
d)任何情況下車輛都應(yīng)符合道路交通安全規(guī)范.
為了便于分析,將信號燈狀態(tài)分為紅燈和綠燈兩種.假設(shè)車輛進(jìn)入通信范圍的時刻為t0,速度為v0,且與交通燈相距Dm,信號燈的循環(huán)周期為ζ,ζ=1,2,···,tgζ代表第ζ個循環(huán)時綠燈的開始時刻,trζ代表第ζ個循環(huán)時紅燈的開始時刻.
當(dāng)前信號狀態(tài)及變化周期如圖1所示,其中縱軸代表信號燈與初始位置的距離,橫軸代表時間.
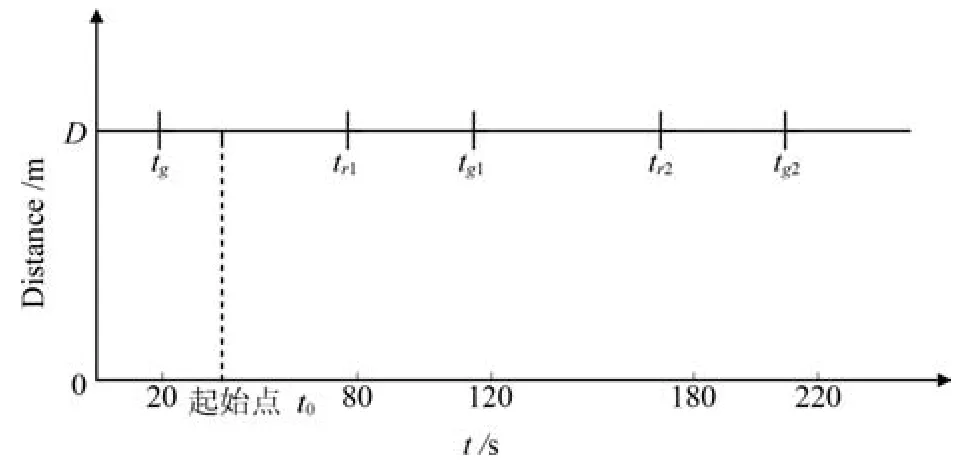
圖1 信號燈循環(huán)狀態(tài)Fig.1 The state of the traffic light cycle
為了更直觀地表示信號燈變化周期,這里引入正弦函數(shù)表示信號燈的紅綠燈變化過程,正半周(函數(shù)值大于零時)表示紅燈,負(fù)半周(函數(shù)值小于零時)表示綠燈.
設(shè)定車輛通過信號燈的時間為tpass,如果車輛不能以當(dāng)前速度勻速通過該信號燈,則車輛通過該路段的過程可描述為:車輛以恒定加速度/減速度a運(yùn)動 ?t時間后,達(dá)到速度vl,速度vl=v0+a?t,此時車輛行駛的距離為D′=v0?t+a?t2;此后,車輛以速度vl勻速行駛剩下的距離,駕駛時長為tpass??t?t0、距離D′′=(v0+a?t)(tpass??t?t0);全程距離關(guān)系滿足D=D′+D′′.
考慮到實(shí)際城市道路環(huán)境及安全要求,為保證在合理范圍內(nèi)的加速度最小,將tpass的值選為紅綠燈切換時刻的臨界值.下面根據(jù)車輛行駛情況按加速、減速及勻速三種情況分別進(jìn)行詳細(xì)討論:
1)如果D<v0(tpass?t0),則車輛可維持當(dāng)前速度安全通過綠燈,無須額外的加減速變換.
2)如果按照上述分析,車輛需加速一段距離后才能通過信號燈路,即a>0,則選取第ζ個循環(huán)紅燈開始的時刻作為車輛通過信號燈的臨界節(jié)點(diǎn),即tpass=trζ,以此來確保在加速過程中的加速度最小,將該過程轉(zhuǎn)化為數(shù)學(xué)表達(dá)式如下:
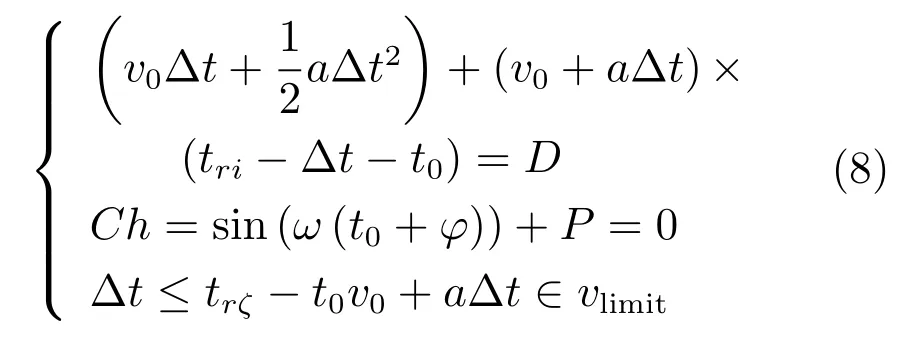
3)如果車輛需減速通過信號燈路,即a<0,則選取tpass=tgζ來確保減速度最小,且符合如下規(guī)則:
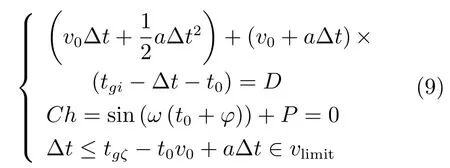
在情況 2)的第一項方程中v0?t+a?t2代表車輛以初始速度v0進(jìn)入信號燈預(yù)測范圍后,以加速度a勻加速駕駛?t時間后的路程;(v0+a?t)(tri??t?t0)代表車輛經(jīng)過加速運(yùn)動后,在剩余路程中,以v0+a?t的速度勻速駕駛(tri??t?t0)時間的路程,為了確保加速度最小,選取通過該段信號燈的駕駛時間tpass=tgζ;方程Ch是信號燈判據(jù),ω、?、P是構(gòu)成信號燈周期的正弦函數(shù)參數(shù);第三項方程表示加速時間?t不應(yīng)超過全程駕駛時間trζ?t0;第四項方程則對速度進(jìn)行限制,vlimit為本文設(shè)定的安全速度限制范圍.情況3)表示車輛減速通過信號燈的表達(dá)式,分析過程同上,在第三項方程中,選取tgζ?t0作為全程駕駛時間,這樣可以確保減速度的最小.考慮油耗與加速度的關(guān)系,本文選取加速度值最小點(diǎn)來求取目標(biāo)速度vtarget.
注1.為了確保加速度與行車時間的平衡,本文考慮車輛以勻速、加速、減速通過信號燈路口的三種不同情況,選取紅綠燈變換的節(jié)點(diǎn)時刻作為tpass的值.相較于文獻(xiàn)[26]中以信號燈狀態(tài)作為節(jié)點(diǎn),本文的方法更為簡明直觀,且可保證每種情況下的加速度變化最小.本文采用正弦函數(shù)描述信號燈變化周期,與文獻(xiàn)[12]的集合形式相比,不僅減少了計算量,表現(xiàn)形式也更為清晰新穎.
2.2 基于油耗優(yōu)化的車速控制
2.2.1 性能指標(biāo)
本文采用MPC實(shí)現(xiàn)車輛油耗優(yōu)化控制.MPC方法是一種特殊的優(yōu)化控制方法,采用MPC控制方法時,控制器不僅利用當(dāng)前和過去的偏差值,還引入預(yù)測模型來預(yù)測未來的偏差值,并通過滾動優(yōu)化過程迭代地計算最優(yōu)控制輸入,從而使未來一段時間內(nèi)的被控量與其期望值的偏差最小.
MPC方法中,車輛方程可表達(dá)成如下形式:
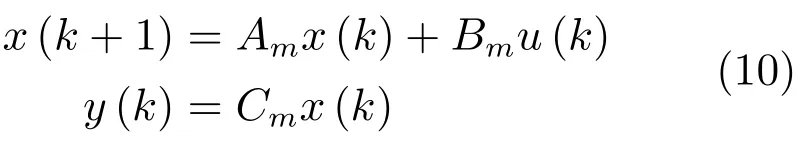
其中,Am、Bm是相應(yīng)的離散系統(tǒng)矩陣,Am=eAeh,采樣周期取為h=0.2.
狀態(tài)方程(10)作為本文MPC控制器預(yù)測模型,設(shè)定NP為預(yù)測步數(shù),也就是最優(yōu)化窗口的長度.為此,將性能指標(biāo)(7)重新寫為如下形式:
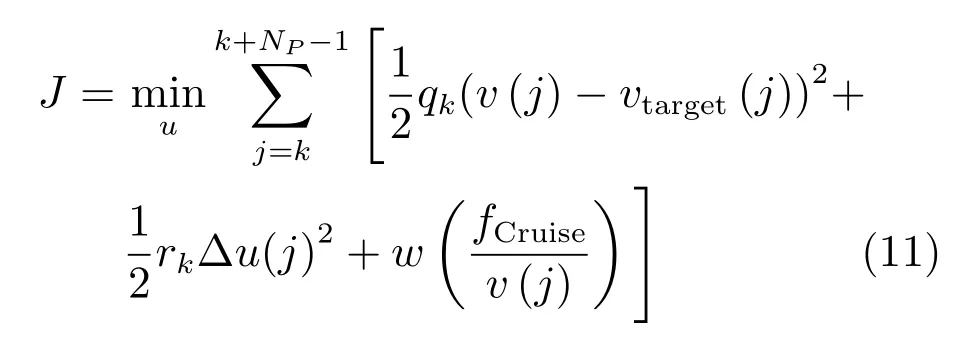
其中,vtarget(j)是由式(8)和(9)得到的車輛參考速度,qk、rk和w為加權(quán)系數(shù).
注2.本文采用MPC方法求解最優(yōu)速度序列時,在速度約束部分采用了實(shí)時變化的設(shè)定速度而非固定的參考速度,且性能指標(biāo)中間接考慮了信號燈狀態(tài)與車輛行駛速度的關(guān)聯(lián),這一性能指標(biāo)非常符合車輛–信號燈協(xié)同控制的實(shí)際需要.
2.2.2 預(yù)測模型重構(gòu)
由于本文設(shè)計的控制輸入u與加速度a大小有關(guān),為確保車輛行駛的平穩(wěn)性,加速度變化應(yīng)盡可能小.因此,我們采用增量式控制策略.為此,引入狀態(tài)和控制量的差值表達(dá)式:?x(k+1)=x(k+1)?x(k),?u(k)=u(k)?u(k?1)
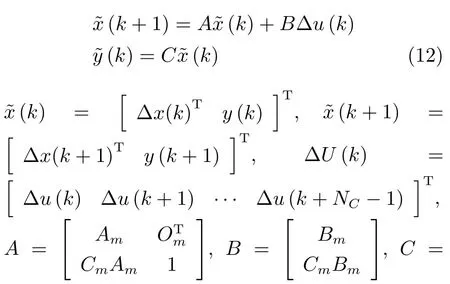
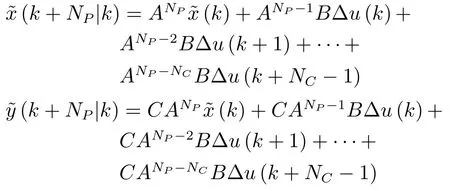
2.2.3 基于Laguerre函數(shù)的控制輸入計算
結(jié)合性能指標(biāo)及狀態(tài)方程不難看出,狀態(tài)方程(12)的預(yù)測輸出(k+m|k)即為性能指標(biāo)(11)的速度v(j),可見,求解最優(yōu)控制輸入使速度輸出和設(shè)定值偏差最小,就可以解決使得預(yù)測輸出(k+m|k)趨近設(shè)定值vtarget的問題.對于該優(yōu)化問題的求解,本文采用Laguerre函數(shù)逼近方法.
首先將控制輸入序列表示為?U=則可將任意預(yù)測輸入用脈沖算子δ和?U來表示,即有?u(k+m)=?U,這里m表示時間序列 (m=0,1,···,NC?1).如果將?U看作系數(shù)向量,很顯然脈沖算子就用來獲取控制軌跡,因而 ?u(k+m)可近似表示為離散多項式函數(shù),本文用如下離散Laguerre函數(shù)來逼近:lN(m)=其中,d=e?λ,λ為時間比例因數(shù).定義向量:則有如下差分關(guān)系式:
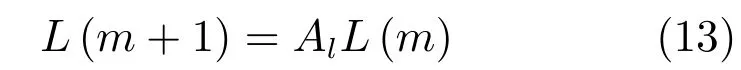
由文獻(xiàn)[27]可知,L2(R+)內(nèi)的任意函數(shù)均可描述為基于Laguerre函數(shù)的正交展開形式.設(shè)離散變量的脈沖響應(yīng)為H(m),則它可描述為Laguerre函數(shù)的N級正交展開形式:
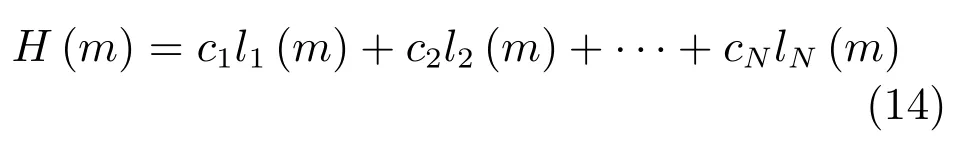
其中,系數(shù)ci滿足如下關(guān)系:
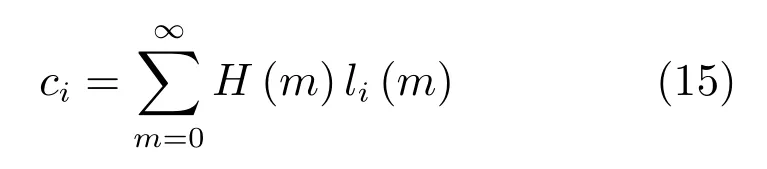
用Laguerre函數(shù)近似離散系統(tǒng)的脈沖響應(yīng)的求解過程如下:首先,生成系統(tǒng)(10)的脈沖響應(yīng)H′(m);然后,根據(jù)式(15)和H′(m)確定參數(shù)序列ci;再根據(jù)式(14)得到基于Laguerre函數(shù)的脈沖響應(yīng)H(m),通過調(diào)節(jié)參數(shù)λ的值,使H(m)逼近脈沖響應(yīng)曲線H′(m).
根據(jù)上述思想,時刻k的控制輸入脈沖響應(yīng)?u(k+m)可表示為
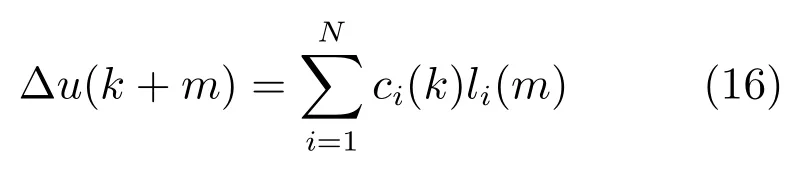
或?qū)憺槿缦孪蛄啃问?
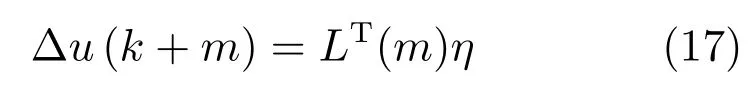
其中,η是N維列向量,
在之后的討論中,用LT(m)η代替?u(k+m),則求解最優(yōu)控制輸入?u(k)就轉(zhuǎn)化為求解序列η的問題.結(jié)合上一節(jié)的討論,k時刻的未來狀態(tài)(k+m)和輸出(k+m|k)可表示如下:
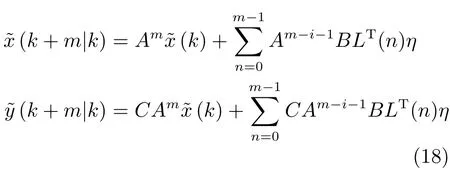
由此可見,求取最優(yōu)向量η即間接得到最優(yōu)解?u(k).
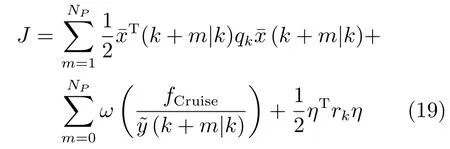
取φT(m)=,結(jié)合方程 (15)可將性能指標(biāo)(16)整理為
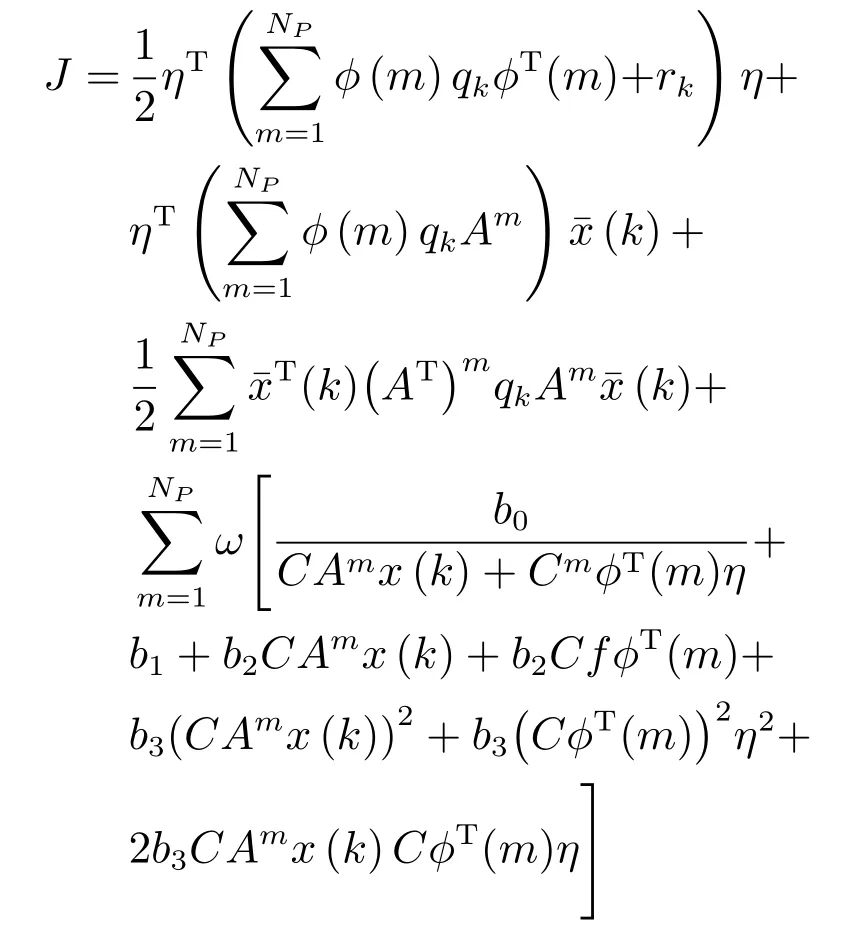
為了得到最優(yōu)解η,性能指標(biāo)J最小化的必要條件為從而得到最優(yōu)的η為
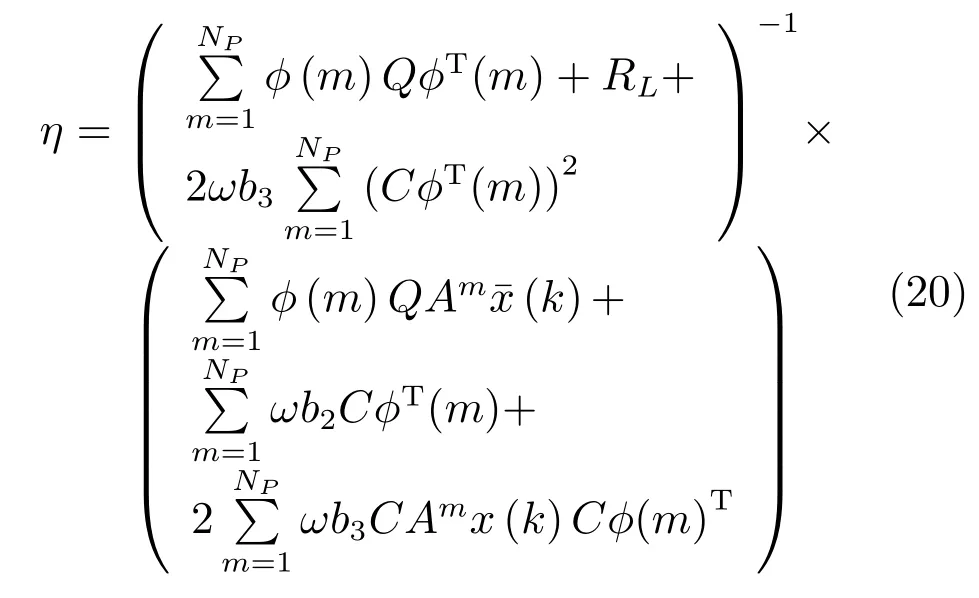
進(jìn)而利用式(17)即得到最優(yōu)控制輸入序列?U=從而完成MPC最優(yōu)控制輸入的求解.
3 仿真結(jié)果及分析
為了驗證上述理論的正確性,本文選取如下參數(shù)進(jìn)行仿真實(shí)驗:信號燈的循環(huán)周期T=100s,其中60s為紅燈(其中包括5s黃燈),40s為綠燈,正弦函數(shù)的角頻率+π,采樣長度為N=100,給定各參考系數(shù)如下:ρ=1m/s2,A=2.2m2,Cd=0.35,dm=5,m=1464kg,δ=0.1,cr=0.015,ud=1.5,ω=110.0,b0=0.1569,b1=0.0245,b2=?7.415×10?4,b3=5.975×10?5,c0=0.07224,c1=0.09681,c2=0.001075[23];本文對比實(shí)驗選取經(jīng)驗駕駛Gipps模型[28].
設(shè)定車輛的初始速度v0=11.5m/s,速度范圍為:vlimit∈[11.1m/s,22.2m/s],為了更好地接近實(shí)際情況,圖2給出了車輛參考速度vtarget隨著信號燈變化的曲線.在圖2(a)中,車輛與依次4個信號燈的距離分別為D1=1300m、D2=2500m、D3=7000m、D4=9000m,仿真結(jié)果顯示在距離D1中,當(dāng)車輛判斷不能勻速通過后,全程以0.03m/s2的加速度駕駛,在第二段距離D2中,車輛全程以0.226m/s2的加速度在當(dāng)前信號燈周期內(nèi)通過路口,在第三段距離D3中,車輛經(jīng)過兩個信號燈周期的時間長度,以0.016m/s2的減速度勻減速通過,在第四段距離D4中,車輛以0.0252m/s2的加速度在綠燈即將結(jié)束時通過.
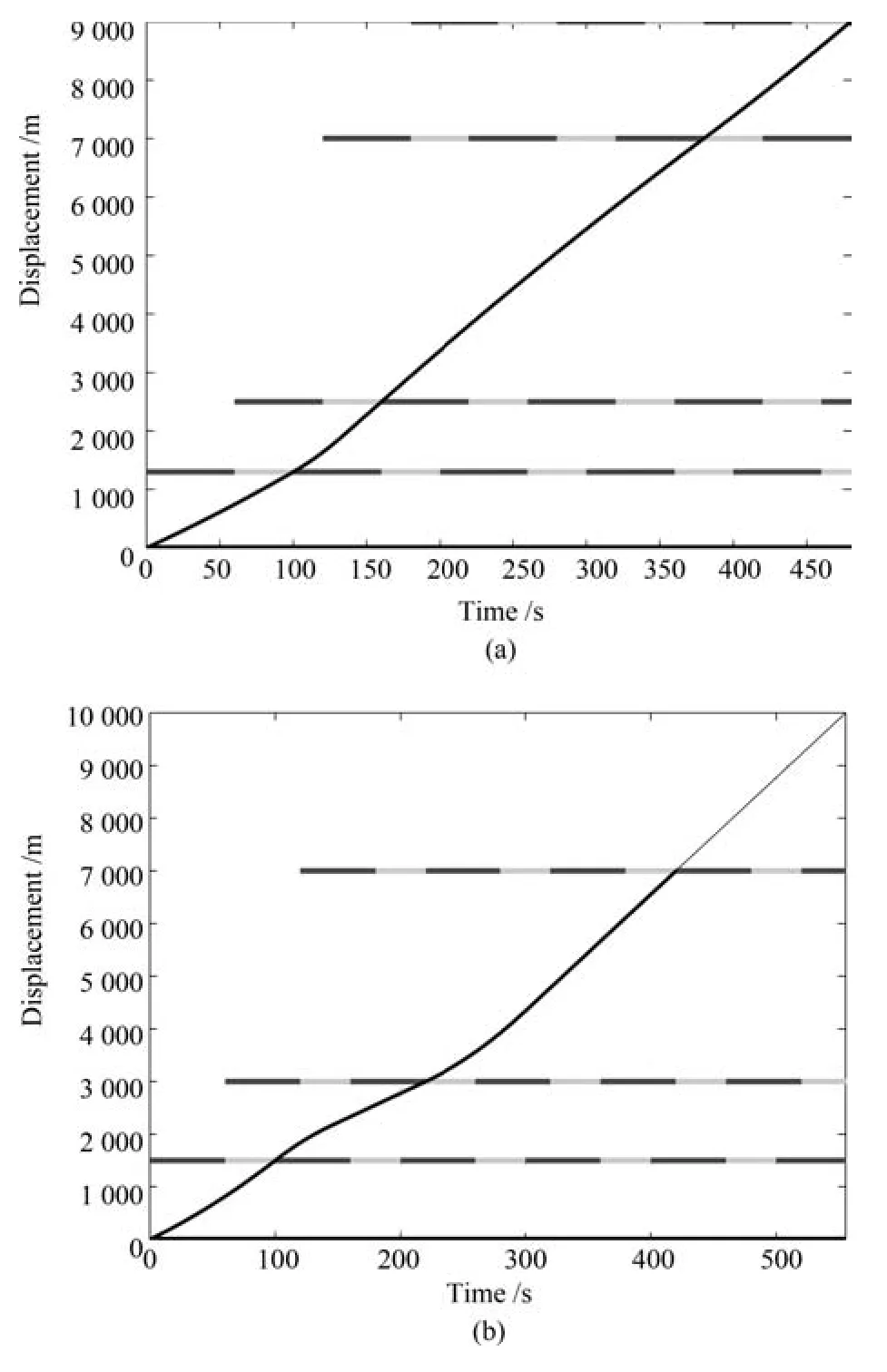
圖2 基于信號燈信息的車輛駕駛距離曲線Fig.2 The vehicle driving distance curve with traffic light information
在圖2(b)中車輛距4個信號燈分別為=1500m、=3000m、=7000m、=10000m,仿真結(jié)果顯示在第一段距離中,車輛以加速度0.07m/s2通過信號燈,在第二段距離中,車輛先以0.164m/s2的減速度減速50s后勻速駕駛,在第三段距離中,車輛先以0.140m/s2加速75s后,維持該速度勻速通過信號燈,在距離中,車輛可以勻速通過第一個循環(huán)的綠燈,無需其他操作.圖2很好地反映出車輛嚴(yán)格遵守文中的駕駛規(guī)則,避免了不必要的加減速以及急剎車操作.圖3給出了上述兩種情況下,運(yùn)用MPC方法和傳統(tǒng)Gipps模型分別對參考速度vtarget進(jìn)行速度跟蹤的曲線,從圖3中可以看出,運(yùn)用MPC方法的車輛可以很好地對參考速度進(jìn)行跟蹤,在每一時間段內(nèi),跟蹤速度與參考速度都較為接近,尤其在通過每一信號燈路口的瞬時,速度波動較小,跟蹤誤差在合理范圍之內(nèi),且在勻速階段跟蹤效果最為理想;而傳統(tǒng)Gipps模型雖然也能較迅速地對參考速度進(jìn)行跟蹤,但其具有很大的時延性,當(dāng)速度波動較大的時候,其不斷累積跟蹤誤差,由圖3(b)可以看出,從第130s時開始的勻速階段,跟蹤誤差累積到最大值,跟蹤效果并不理想.
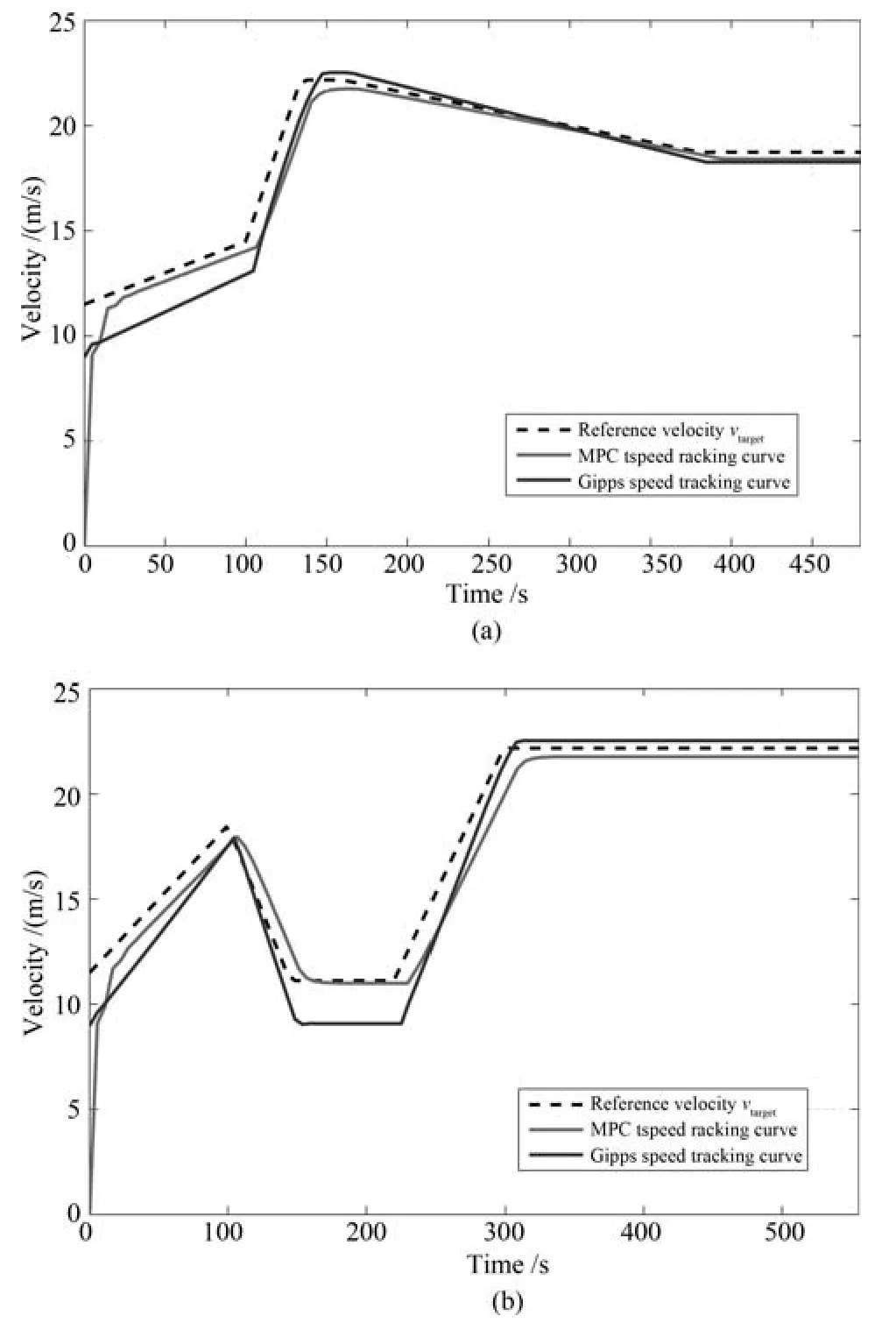
圖3 速度跟蹤曲線Fig.3 The speed tracking curve
圖4給出了在兩種情況下通過MPC方法得到的最優(yōu)控制輸入曲線,與圖3中速度的加、減變化相對應(yīng).當(dāng)控制輸入在零值以上,車輛處于加速狀態(tài);否則,控制輸入值應(yīng)相應(yīng)減小,車輛開始減速,在駕駛過程中,控制輸入能夠維持在一定的界限范圍內(nèi),且控制輸入整體波動比較平穩(wěn).
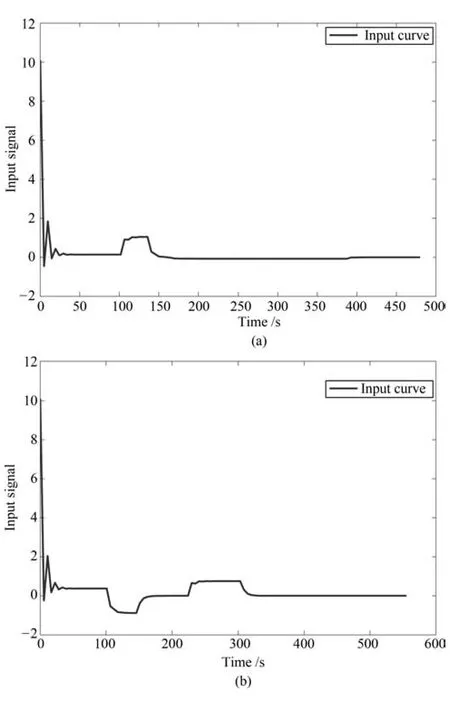
圖4 MPC車輛輸入曲線Fig.4 The input curve of the MPC-vehicle
圖5表示在MPC方法中,輸入差值?u的變化,輸入差值越接近0,代表實(shí)際輸入與限制范圍的偏差越小,也就是加速度的變化越小,系統(tǒng)狀態(tài)越穩(wěn)定.實(shí)驗表明,輸入?u在零值附近穩(wěn)定波動,在加速過程中會產(chǎn)生小幅震蕩,但最終都穩(wěn)定趨于0,運(yùn)用MPC方法,具有良好的穩(wěn)定性,由于速度的波動較小,為乘客和駕駛員提供了舒適性,速度的合理控制,在一定程度上增加了交通的安全性.
圖6給出了兩種情況下,運(yùn)用MPC方法駕駛一段時間后的油耗曲線,并且與傳統(tǒng)Gipps跟蹤速度方法進(jìn)行對比,對比實(shí)驗顯示,雖然在速度跟蹤性能上,Gipps方法也能很好地對目標(biāo)速度進(jìn)行跟蹤,但是采用傳統(tǒng)Gipps方法對車輛進(jìn)行控制時,其瞬時加速度較大,油耗量也明顯增加,不能很好地降低油耗,產(chǎn)生了不必要的燃油浪費(fèi)以及空氣污染;而MPC方法在每一個信號燈路段耗油量都有所降低,尤其當(dāng)速度變化頻繁的時候,油耗量明顯低于采用Gipps控制的車輛,而隨著駕駛距離的增加,累計油耗節(jié)約量也顯著提高.由此可以看出,本文提出的基于MPC的車輛環(huán)保駕駛方法,不僅能很好地根據(jù)信號燈信息進(jìn)行速度跟蹤,而且能夠明顯降低車輛油耗,更加適合于城市交通環(huán)境中的自動駕駛技術(shù).
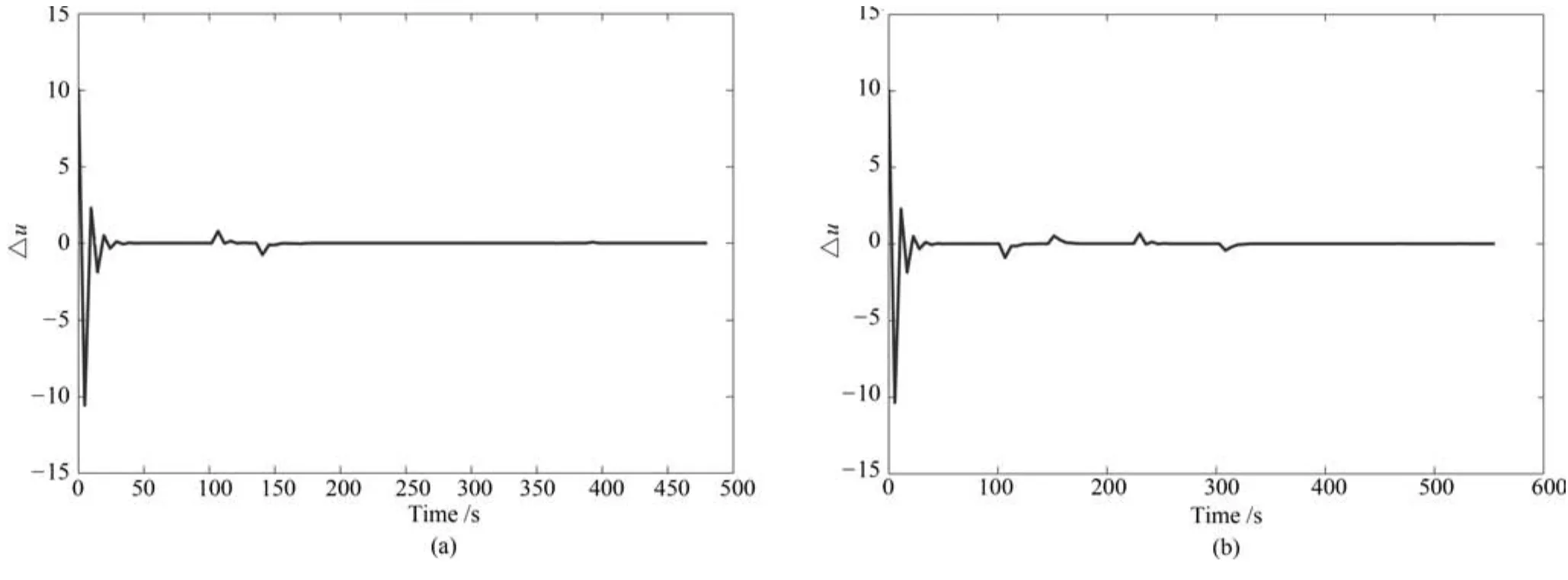
圖5 MPC車輛輸入差值曲線Fig.5 The input difference curve of the MPC-vehicle

圖6 車輛油耗曲線Fig.6 The input curve of the MPC-vehicle
4 結(jié)論
標(biāo),采用模型預(yù)測控制方法得到可保證行駛安全的油耗最優(yōu)控制策略.仿真實(shí)驗表明,采用本文的方法后,車輛可實(shí)現(xiàn)免停車通過前方信號燈,且明顯比傳統(tǒng)的控制方法更為省油.由于對參考速度進(jìn)行實(shí)時規(guī)劃,所以本文的駕駛策略更適合城市交通應(yīng)用.不過,本文并未考慮存在前方車輛的情況,如何考慮前方車輛進(jìn)行車輛跟蹤及信號燈控制協(xié)同設(shè)計,這一問題值得進(jìn)一步研究.
本文提出一種基于信號燈信息預(yù)測和模型預(yù)測控制來降低城市交通中車輛油耗的環(huán)保駕駛策略.車輛通過通信網(wǎng)絡(luò)獲取當(dāng)前信號燈狀態(tài)及其周期,且根據(jù)安全和節(jié)油規(guī)則,對車輛不停車通過信號燈的最佳速度進(jìn)行規(guī)劃.然后結(jié)合油耗和控制性能指
1 Zhao Na,Yuan Jia-Bin,Xu Han.Survey on intelligent transportation system.Computer Science,2014,41(11):7?11(趙娜,袁家斌,徐晗.智能交通系統(tǒng)綜述.計算機(jī)科學(xué),2014,41(11):7?11)
2 Yang Kai.China′s automobile market review of 2014 and sales prediction in 2015.Auto Industry Research,2014,(4):4?11(楊凱.2014中國汽車市場回顧及2015銷量預(yù)測.汽車工業(yè)研究,2014,(4):4?11)
3 Mukhtar A,Xia L K,Tangt B.Vehicle detection techniques for collision avoidance systems:a review.IEEE Transactions on Intelligent Transportation Systems,2015,16(5):2318?2338
4 Xiao L Y,Gao F.A comprehensive review of the development of adaptive cruise control systems.Vehicle System Dynamics,2010,48(10):1167?1192
5 Dey K C,Yan L,Wangx J,Wang Y,Shenh Y,Chowdhury M,Yu L,Qiu Cx,Soundararaj V.A review of communication,driver characteristics,and controls aspects of cooperative adaptive cruise control(CACC).IEEE Transactions on Intelligent Transportation Systems,2016,17(2):491?509
6 Nkoro A B,Vershinin Y A.Current and future trends in applications of Intelligent Transport Systems on cars and infrastructure.In:Proceedings of IEEE 17th International Conference on Intelligent Transportation Systems.Qingdao,China:IEEE,2014.514?519
7 Butakov V A,Ioannou P.Personalized driver assistance for signalized intersections using V2I communication.IEEE Transactions on Intelligent Transportation Systems,2016,17(7):1910?1919
8 Kamal M A S,Mukai M,Murata J,Kawabet.Development of ecological driving system using model predictive control.In:Proceedings of the 2009 ICCAS-SICE.Fukuoka:IEEE,2009.3549?3554
9 Kamal M A S,Mukai M,Murata J,Kawabet.Ecological vehicle control on roads with up-down slopes.IEEE Transactions on Intelligent Transportation Systems,2011,12(3):783?794
10 Ichiharat,Kumano S,Yamaguchi D,Sato Y,Suda Y.Driver assistance system for eco-driving.In:Proceedings of 16th ITS World Congress and Exhibition on Intelligent Transport Systems and Services.Stockholm,Sweden:ITS,2009.
11 Yangx Y,Li D,Zheng P J.Effects of eco-driving on driving performance.Applied Mechanics&Materials,2012,178?181:2859?2862
12 Asadi B,Vahidi A.Predictive cruise control:utilizing upcoming traffic signal information for improving fuel economy and reducing trip time.IEEE Transactions on Control Systems Technology,2011,19(3):707?714
13 Cheng Q,Nouveli′ere L,Or fi la O.A new eco-driving assistance system for a light vehicle:energy management and speed optimization.In:Proceedings of the 2013 IEEE Intelligent Vehicles Symposium(IV).Gold Coast,Australia:IEEE,2013.1434?1439
14 Sungt W,Shiu L C,Lin Ft,Yang C S.A speed control scheme of eco-driving at road intersections.In:Proceedings of the 3rd International Conference on Robot,Vision and Signal Processing.Kaohsiung,Taiwan,China:IEEE,2015.51?54
15 Xiang Xh,Zhou K,Zhang W B,Qin Wh,Mao Q Z.A closed-loop speed advisory model with Driver′s behavior adaptability for eco-driving.IEEE Transactions on Intelligent Transportation Systems,2015,16(6):3313?3324
16 Kamal M A S,Mukai M,Murata J,Kawabet.Ecological driver assistance system using model-based anticipation of vehicle-road-traffic information.IET Intelligent Transport Systems,2010,4(4):244?251
17 Kamal M A S,Mukai M,Murata J,Kawabet.Model predictive control of vehicles on urban roads for improved fuel economy.IEEE Transactions on Control Systems Technology,2013,21(3):831?841
18 Kamal M A S,Mukai M,Murata J,Kawabet.Ecological driving based on preceding vehicle prediction using MPC.IFAC Proceedings Volumes,2011,44(1):3843?3848
19 Azpilicueta L,Vargas-Rosales C,Falcone F.Intelligent vehicle communication:deterministic propagation prediction in transportation systems.IEEE Vehicular Technology Magazine,2016,11(3):29?37
20 Nguyen V,Kim Ott,Dangt N,Moon S I,Hong C S.An efficient and reliable green light optimal speed advisory system for autonomous cars.In:Proceedings of the 18th Asia-Paci fi c Network Operations and Management Symposium(APNOMS).Kanazawa:IEEE,2016.1?4
21 Zhengx Z,Zhang L G,Kholodov Y.Model predictive control of eco-driving for transit using V2I communication.In:Proceedings of the 34th Chinese Control Conference(CCC).Hangzhou,China:IEEE,2015.2511?2516
22 Guant Y,Frey C W.Predictive fuel efficiency optimization using traffic light timings and fuel consumption model.In:Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems(ITSC).The Hague,The Netherlands:IEEE,2013.1553?1558
23 Wang Q,Guo G,Cai B B.Distributed receding horizon control for fuel-efficient and safe vehicle platooning.Science China Technological Sciences,2016,59(12):1953?1962
24 Huang S,Ren W.Safety,comfort,and optimal tracking control in AHS applications.IEEE Control Systems,1998,18(4):50?64
25 Seredynski M,Dorronsoro B,Khadraoui D.Comparison of green light optimal speed advisory approaches.In:Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems(ITSC).The Hague,The Netherlands:IEEE,2013.2187?2192
26 Mandava S,Boriboonsomsin K,Barth M.Arterial velocity planning based on traffic signal information under light traffic conditions.In:Proceedings of the 12th International IEEE Conference on Intelligent Transportation Systems.St.Louis,America:IEEE,2009.1?6
27 Wang L P.Model Predictive Control System Design and Implementation Using MATLAB?,London:Springer-Berlin,2009.1?148
28 Gipps P G.A behavioural car-following model for computer simulation.Transportation Research Part B:Methodological,1981,15(2):105?111

