永磁同步電機的自適應預測比例–積分–諧振電流控制

于子淞　王大志　陶冶

永磁同步電機(Permanentmagnetsynchronous motor,PMSM)功率密度高、電流輸出轉矩比小,被廣泛應用于航天、數控機床等高精度調速場合[1?3].交流調速系統通常采用速度外環級聯電流內環的控制結構.其中,電流控制性能決定了轉矩控制精度和電機損耗.常規PID控制簡單易行,但對系統參數和外界擾動的魯棒性較差.針對這一缺點,文獻[4?8]分別提出自適應PID 控制[4]、滑模控制[5]、無差拍控制[6]、預測控制[7?8],以提高電流控制精度和系統對電機參數、電壓擾動的魯棒性.

電機相電流諧波源可等效為周期電壓擾動,擾動電壓通常由電壓源逆變器非線性畸變、轉子非正弦反電動勢和磁飽和等因素引起[9].重復電流控制策略[10]可有效抑制周期擾動電壓,但當電機運行于低速時,存儲一個周期內的電流數據占用系統內存較多.迭代學習控制[11]通過在線反復修正相電流幅值和相位,可完全消除諧波電流,但計算量較大.比例–積分–諧振電流控制策略(Proportionalintegral-resonant controller,PI-RES)[12]簡單易行,可有效抑制周期擾動電壓,已廣泛應用于風力發電及交流調速領域.然而,這種常規的PI-RES控制器只是內模控制器的等效并聯形式,并不是真正意義上的漸近穩定并聯控制器.同時,數字控制系統存在一個采樣周期的輸入延時,當系統采樣頻率/電流輸出頻率(fs/fo)小于10時,電流將出現震蕩失穩現象[13].文獻[12]采用電流前饋補償,消除了電流超調,但未對擾動進行預測補償.文獻[14]利用高階濾波器最優逼近包含延時的系統誤差模型,但系統采樣頻率低于2.5kHz時,電流不穩定.文獻[15]在電流環中加入了有源阻尼衰減相,有效抑制了輸入延時對解耦控制的影響.文獻[16]采用二階pade模型近似系統輸入延時,通過最優配置系統根軌跡法削弱了輸入延時對電流控制的影響,但未研究算法對模型參數的魯棒性.

本文通過將多種PI-RES控制器化為統一的狀態空間表達形式,分析系統輸入延時對電流控制穩定性的影響.針對系統輸入延時和電流諧波問題,提出一種自適應預測比例–積分諧振(Adaptive predictive proportional-integral-resonant,APPIRES)電流控制策略.該方法可在電機電阻、電感參數未知的情況下預測電流指令、電壓擾動和電流控制誤差.通過執行預測量的反饋控制,補償系統輸入延時和相電流諧波,算法收斂性分析保證了所提控制器的漸近穩定性.最后,通過仿真研究驗證了所提算法的有效性.

1　 輸入延時對傳統PI-RES控制的影響分析

1.1　 表貼式PMSM電氣模型

逆變器驅動永磁同步電機相電流通常包含6n±1(n為自然數)次諧波,可將電流諧波源等效為頻率為6n±1次周期擾動電壓,在同步旋轉坐標系下該擾動電壓頻率為6n次[9].考慮控制器輸入延時和周期擾動電壓的同步旋轉坐標系下表貼式PMSM電氣模型:

式中,下標D表示延時時間,分別為t?D時刻d、q軸控制器輸出電壓指令,分別為t時刻d、q軸各次諧波擾動電壓的總和,id、iq分別為d、q軸電流,R、L、ωe、?f分別為定子電阻、電感、轉子電角速度和永磁體磁鏈.

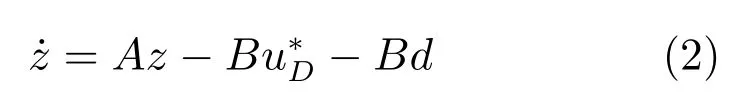
式中

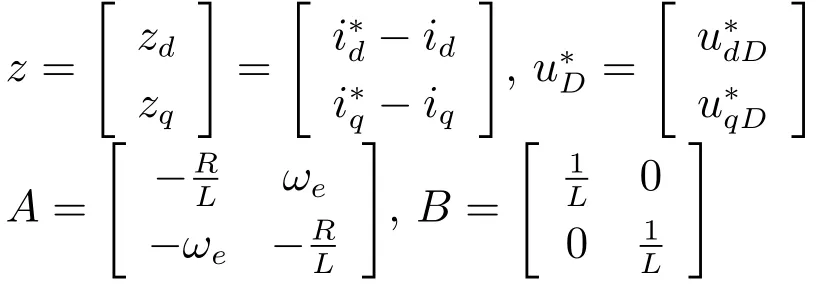
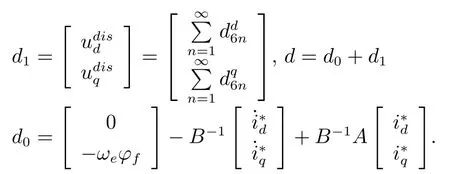
當電機運行于穩態時,d0為恒定值,d1為三角函數的級數和,因此擾動d可表示為

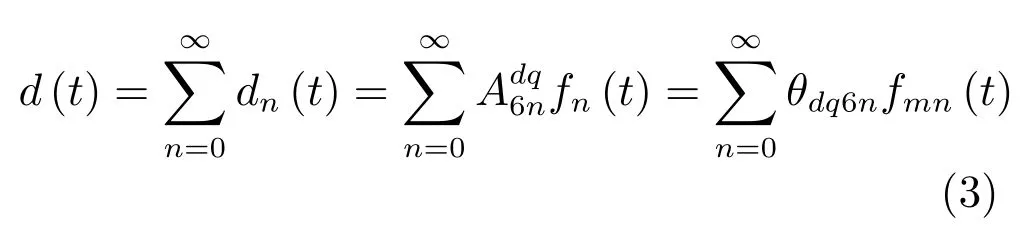
式中

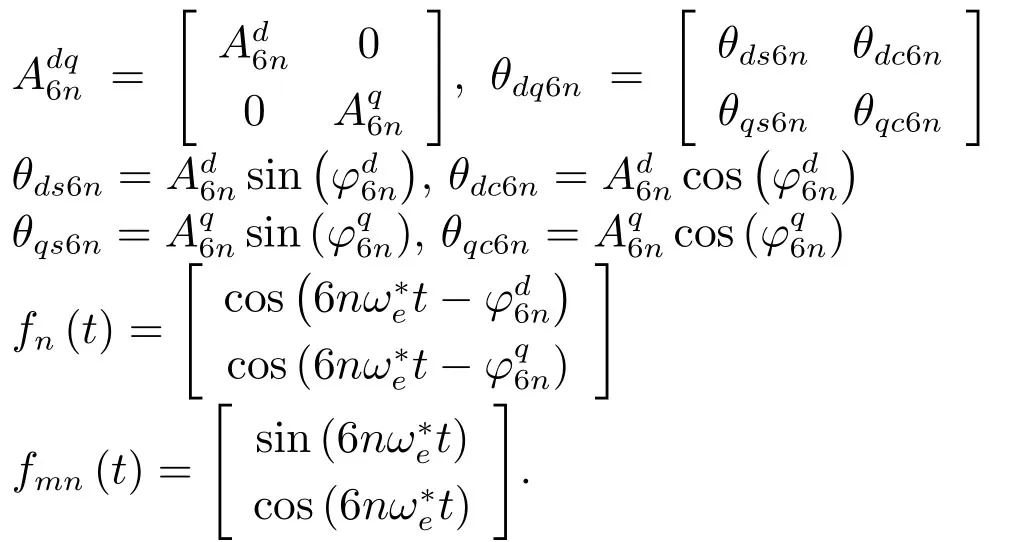
1.2　傳統PI-RES控制器的等效狀態空間形式

傳統PI-RES控制策略通過在系統諧振頻率處并聯諧振器,可實現無靜差抑制系統周期擾動[9].這里為分析方便,令式(3)中n=0～2,則所需設計的PI-RES控制器可表示為[9,12,16]

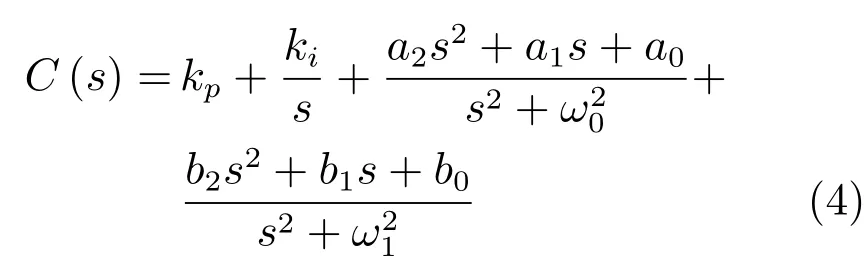
式中,s為拉氏復變量,kp、ki、a0～a2、b0～b2分別為調節器參數.將式(4)中各項分式通分得:

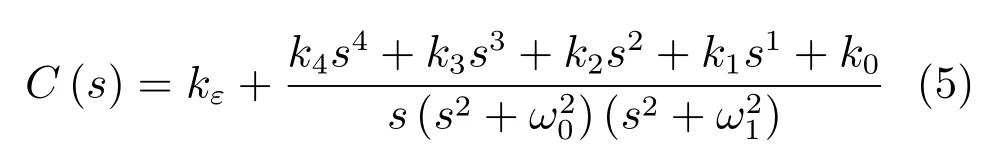
式中

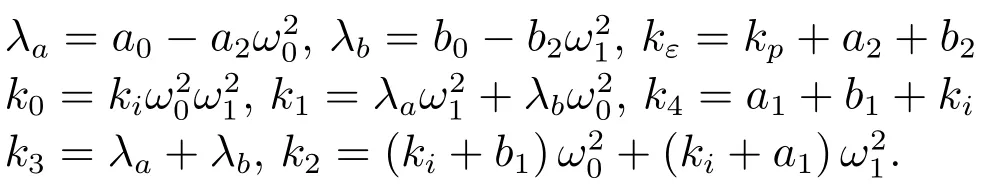
由文獻[17]知,式(5)為內模控制器,系統模態可表示為

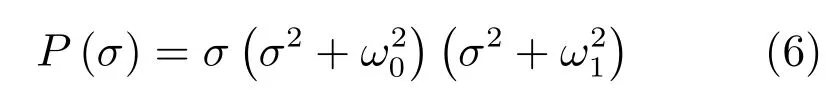
為分析方便,暫不考慮系統輸入延時,即D=0,令ε=P(σ)z為擴展誤差空間狀態分量,由式(2)、(6)建立擴展電流誤差空間方程[17]:

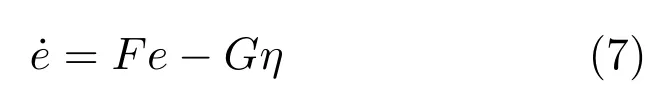
式中

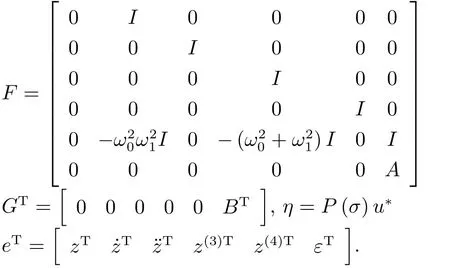
其中,z(i)表示z的i階導數,系數0為2階零矩陣,I為2階單位矩陣.由式(7)知,只需設計狀態反饋矩陣Kr使Fc=F?GKr為Hurwitz矩陣,即可得到漸近穩定的內模控制器.由式(6)知,雙輸入系統(7)的解耦PI-RES控制器所對應的的狀態反饋矩陣為

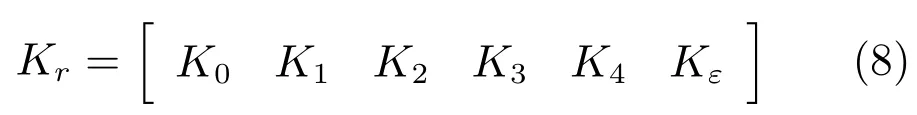
式中

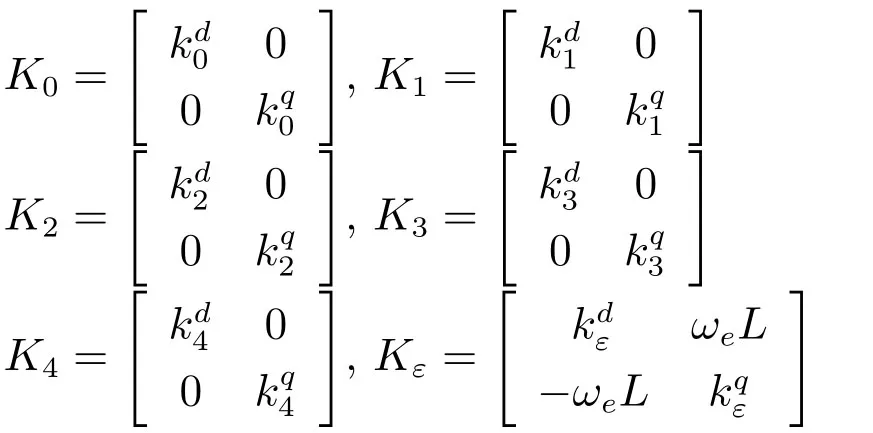
其中,上標d、q分別對應直、交軸內模控制器參數,由系統矩陣A知,ωeL為耦合項,因此,Kε中ωeL為電流解耦項.

注.由式(5)～(8)知,PI-RES控制器需要合理選取并聯諧振器的參數以保證系統漸近穩定.因此,PI-RES控制器并不是真正的并聯型漸近穩定控制器.

1.3　輸入延時對電流控制的影響

由第1.2節分析可知,考慮系統輸入延時后,電流解耦PI-RES控制器所對應的狀態反饋為

式中,eD=λ(t)e為t?D時刻誤差狀態,e為t時刻誤差狀態,λ(t)為等效延時系數矩陣.由式(9)得閉環誤差空間系統為

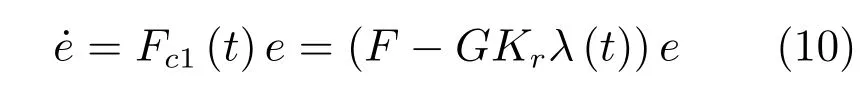
式中,Fc1(t)=F?GKrλ(t)為擴展電流誤差空間系統矩陣,λ(t)為對應維數的分塊對角時變等效延時矩陣,其對角線元素所構成的矩陣為

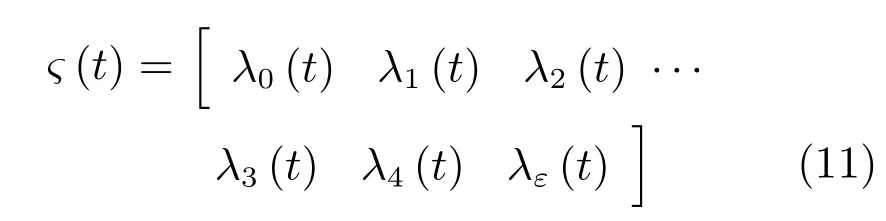
式中,λ0、λ1、λ2、λ3和λε均為對角矩陣.

由式(8)～(11)知,考慮系統輸入延時后的反饋矩陣為

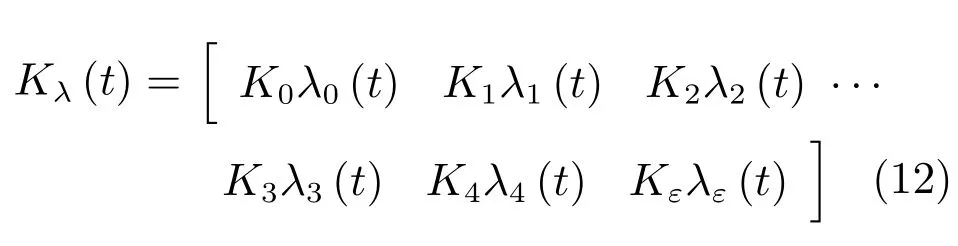
由式(11)和(12)知,當λ(t)對角線元素為1時,系統矩陣Fc1(t)=Fc,即輸入延時對系統無影響.當λ(t)對角線元素不為1時,系統矩陣Fc1(t)/=Fc,即輸入延時對閉環系統的動態性能和穩定性產生了影響.例如,由式(8)和(9)知,kε對應比例反饋系數,當kε取值大于電機時間常數且λε(t)的系數小于零時,系統將發散.因此,需消除由輸入延時引起的系統失穩隱患.

2　APPI-RES電流控制器設計

為消除系統輸入延時對電流環穩定性的影響,實現低fs/fo工況下的漸近穩定并聯諧振電流控制,需要對系統狀態和擾動進行預測.

2.1　擾動預測

考慮電機電阻、電感參數未知,但其變化的界已知時,設計系統(2)的自適應諧振擾動觀測器:

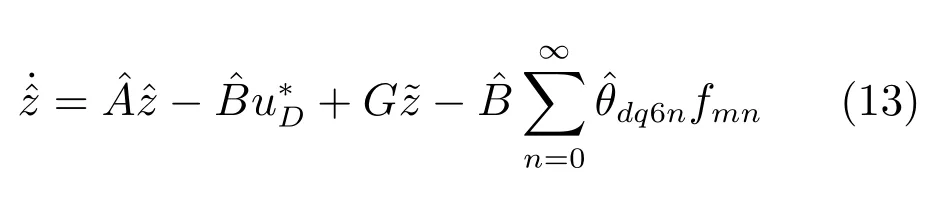
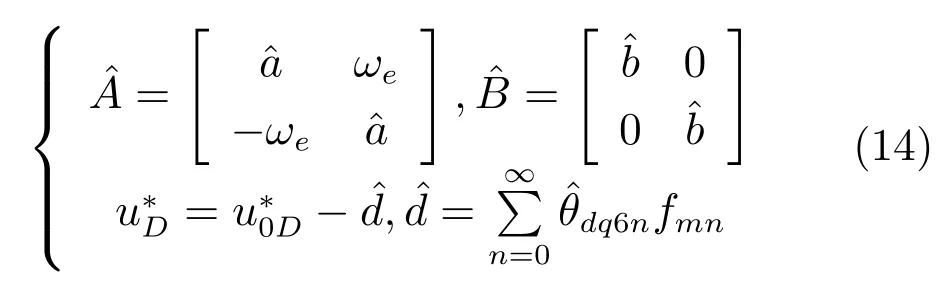
將式(2)和(13)做差得:

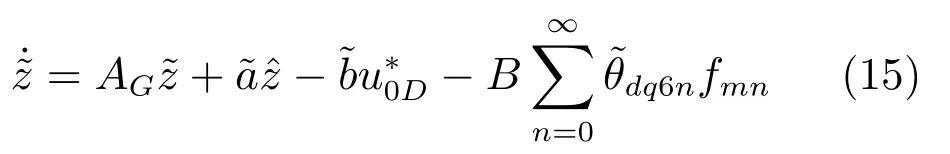
建立觀測誤差系統(15)的Lyapunov函數:

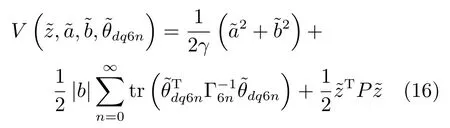
式中,Γ6n為正定對稱矩陣,α、γ為正常數,tr(·)為求矩陣跡運算符號,P為正定對稱矩陣,滿足:

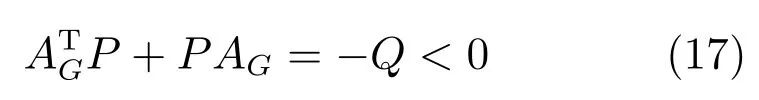
式中,Q為正定對稱矩陣.為簡化運算,取P=I2×2,I2×2為2階單位陣.

對Lyapunov函數(16)求導得:

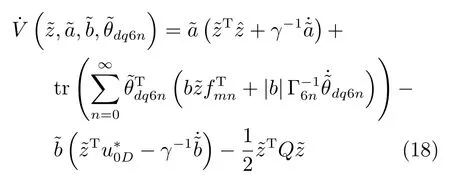
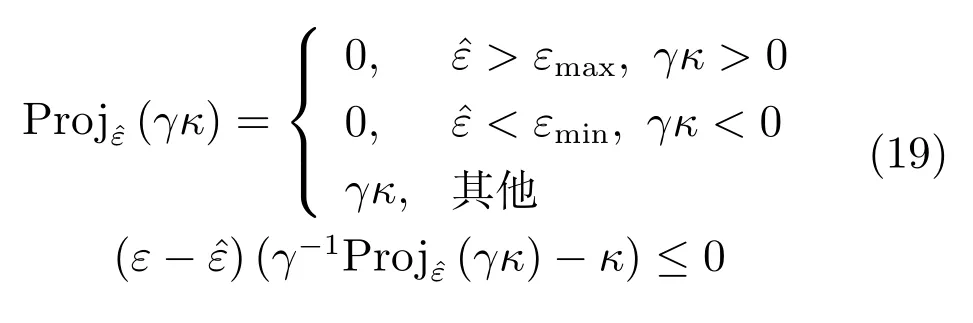
選擇自適應率:

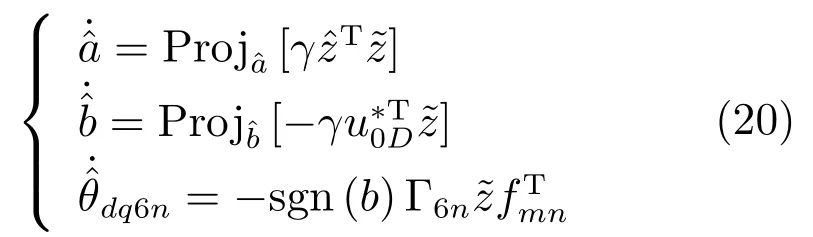
式中,sgn(·)為符號函數.

由式(17)～(20)知,＜0,當t→∞時,→θdq6n,即觀測系統漸近穩定.

由式(3)、(14)、(20)得擾動觀測值:

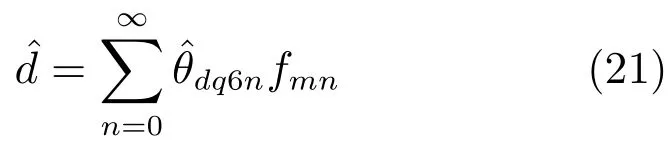
頻率已知、幅值和初始相位未知的正弦函數v(t)=Msin(ωt+?0)滿足:

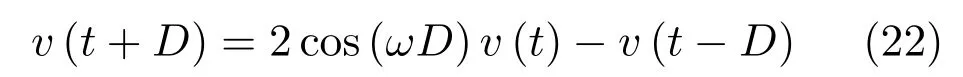
當n/=0時,由式(21)和(22)得擾動預測值:

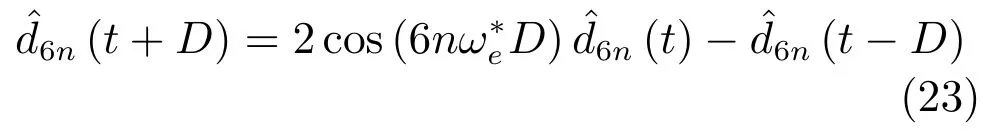
當n=0時,上式可簡化為

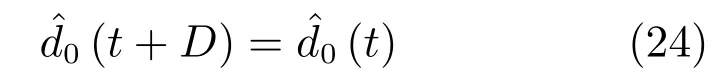
2.2　狀態預測

當t時刻誤差系統狀態z(t)已知時,t+D時刻誤差系統狀態可表示為[9]

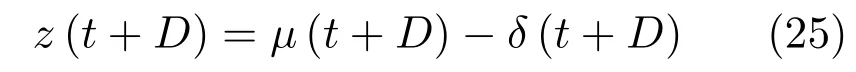
式中

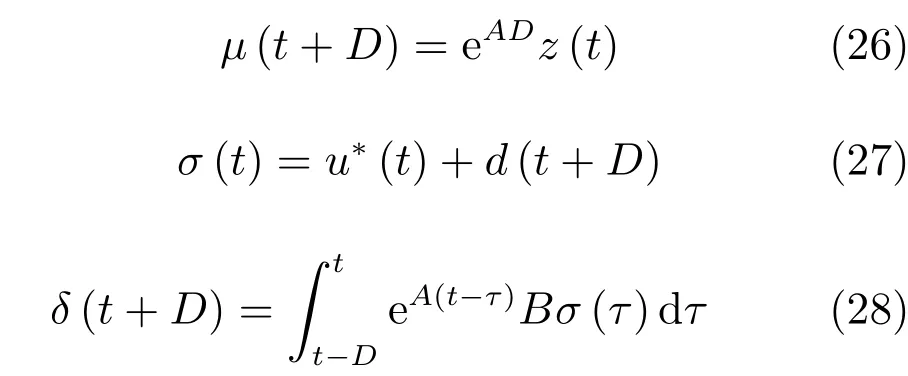
其中,μ(t+D)為t時刻零輸入響應,δ(t+D)為t時刻零狀態響應.進一步,將式(26)～(28)表示為狀態空間形式:式中,δ(D)、μ(D)為系統初始狀態.

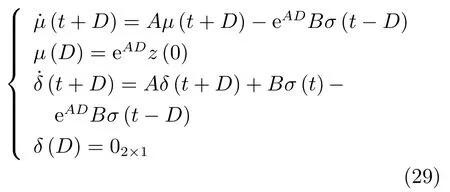
由式(2)、(14)知,系統矩陣及其觀測矩陣滿足:

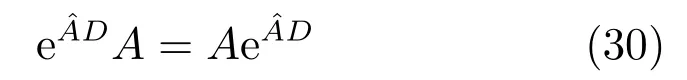
利用第2.1節所得系統參數和擾動的估計值得t+D時刻誤差系統狀態z(t+D)的預測值:

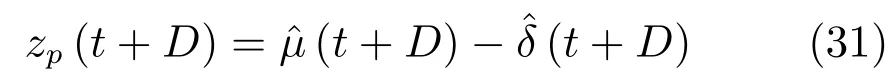
式中

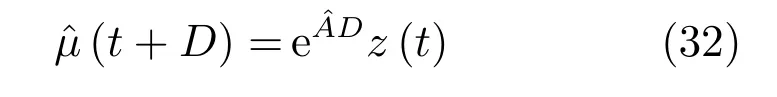
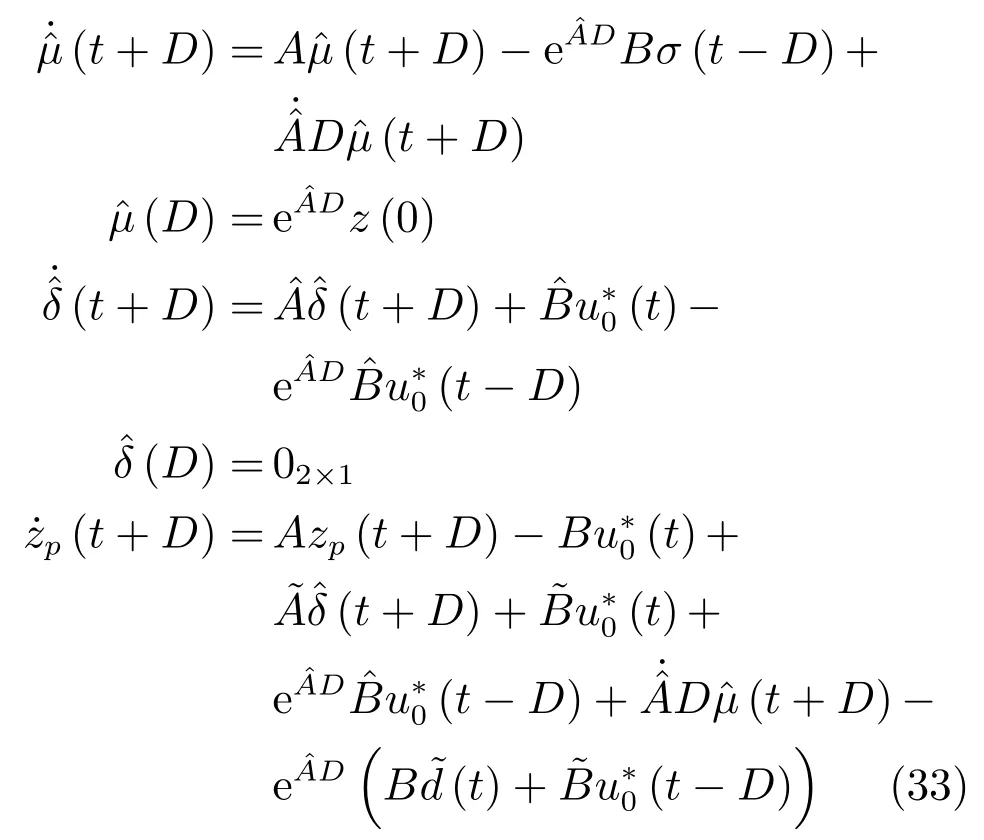
2.3　穩定性分析

由式 (2)、(25)、(29)、(31)、(33)得系統狀態預測誤差:

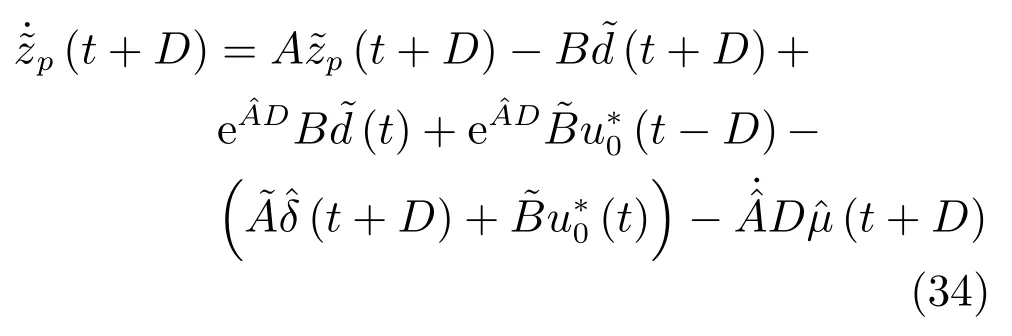
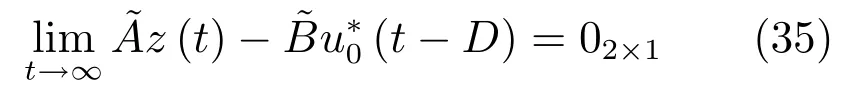
由式 (30)、(31)、(34)、(35)得:

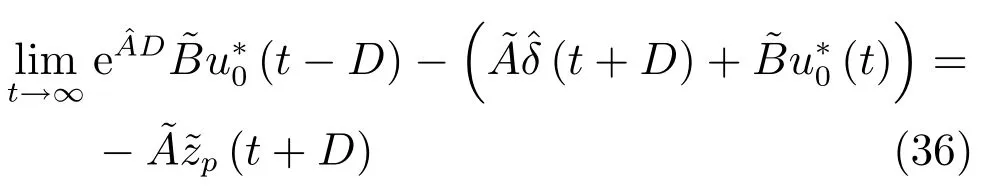
因此,當t→∞時,式(34)可化為

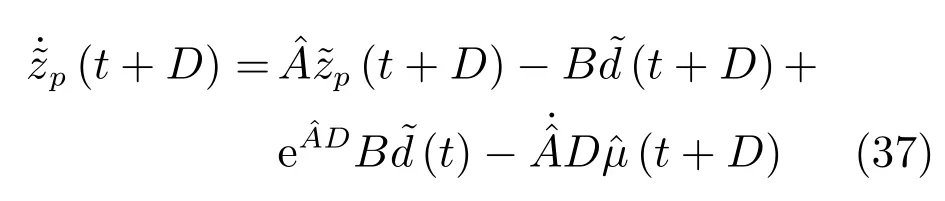
由第2.1節分析可知:

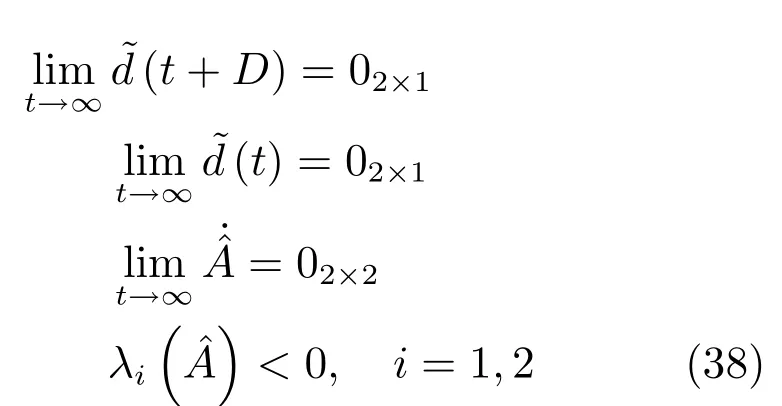
式中,λi為的特征值.由式(37)和(38)得:

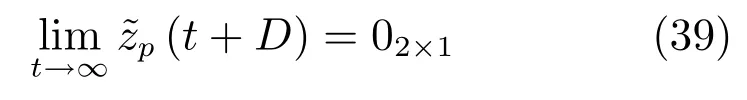
設計控制器:

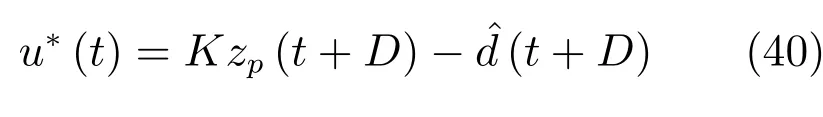
式中,狀態反饋增益矩陣K保證AK=A?BK漸近穩定.閉環系統可表示為

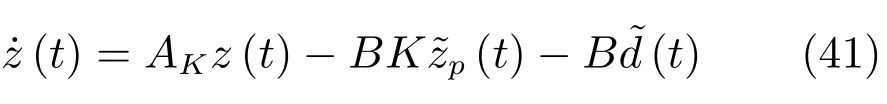
因此,由式(38)～(40)知,式(41)為漸近穩定系統.執行APPI-RES電流控制策略的步驟如下:

步驟1.根據系統模型(2)建立自適應諧振擾動觀測系統(13),t時刻參數自適應率和電壓擾動分別為式(20)和(21).

步驟2.根據式(23)和(24)預測系統擾動,求得t+D時刻系統擾動.

步驟3.利用步驟1中參數自適應率和步驟2中的擾動預測值,根據(31)～(33)預測系統(2)在t+D時刻的狀態.

注.系統未知參數慢變的假設條件可保證未知參數在t到t+D時間內不變.因此,由步驟1中系統未知參數自適應率(20)所求得t時刻系統估計參數可用于t+D時刻系統狀態的預測.

步驟 4.根據(34)～(39)的穩定性證明可得t時刻系統漸近穩定控制器(40).

基于APPI-RES電流控制策略的PMSM系統框圖如圖1所示.

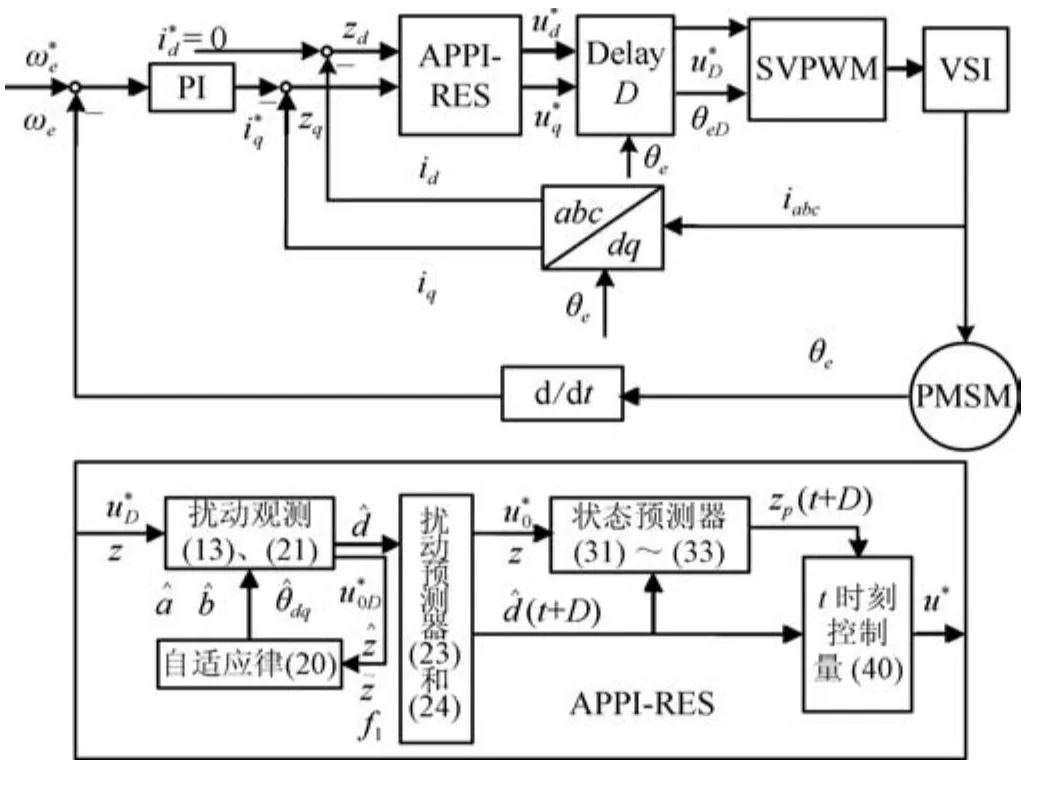
圖1　 采用APPI-RES電流控制器的PMSM驅動系統框圖Fig.1　Block diagram of PMSM driving system using APPI-RES current controller

3　仿真研究

為驗證APPI-RES電流控制器的有效性,在Matlab/Simulink仿真環境下搭建了永磁同步電機調速系統仿真平臺.仿真中,永磁同步電機參數如下:定子電阻R=2.93?,定子d軸和q軸上的電感Ld=Lq=7mH,永磁體磁鏈?f=0.125Wb,轉子磁極對數p=2,轉動慣量J=1.16×10?4kg·m2,粘滯摩擦系數F=2.1×10?4N·m·s.系統其他參數如下:母線電壓Vdc=400V,死區時間3μs,電流環采樣時間100μs,速度環采樣時間200μs.仿真驗證中,速度環所用PI調節器的比例系數Kps=0.5,積分器系數Kis=10,電流環PI-RES控制器形式為:

3.1　 小諧振增益下的PI-RES與APPI-RES電流控制對比仿真研究

根據前文的分析,小諧振器增益下,1個采樣周期的延時不會使系統震蕩.仿真中,只注入VSI死區產生5、7、11、13等奇次諧波電流.電機低速輕載運行時,VSI非線性畸變電壓使相電流畸變較嚴重.因此仿真中電機負載0.1Nm,給定轉速300r/min,模擬低速輕載運行工況.分別采用PI、PI-RES、APPI-RES電流控制器.其中,PIRES控制器參數為:kpc=20、kic=4500、kresn=2000,n=1～6.APPI-RES控制器參數為:式(13)中反饋增益陣G為對角陣,取G11=G22=10000,式(20)中γ=15000、Γ6n為對角陣,取Γ6n11=Γ6n22=10000,式(40)中K為對角陣,取K11=K22=20.如圖2和3所示,PI電流控制器抑制VSI死區電壓的能力較差,相電流中含有大量的6n±1次諧波,電流畸變率(Total harmonic distorition,THD)為22.79%.PI-RES和APPIRES控制器所并聯的諧振器數量可根據電流控制精度和運算速度折中選取.這里選擇并聯諧振器數量為6,即諧振器只能消除36±1次之前的諧波電流.由圖4～7知,PI-RES和APPI-RES兩種電流控制器都能很好地抑制6n±1次諧波電流,THD分別為1.85%和1.56%.由第1.2節、第1.3節分析可知,在小諧振器增益情況下PI-RES控制器可保證系統漸近穩定,且仿真所取延時時間較小,擾動電壓在延時時間內變化小,因此,PI-RES控制器能夠實現較高精度的電流控制.仿真結果同樣驗證了第2.2節中對所提APPI-RES電流控制策略理論分析的有效性.

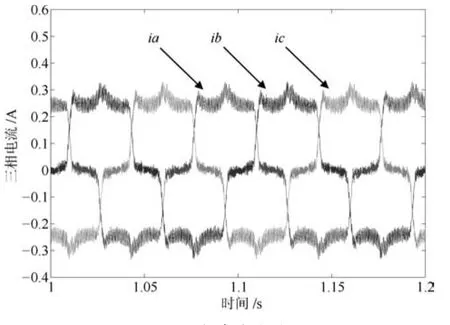
圖2　相電流(PI)Fig.2　Phase currents(PI)

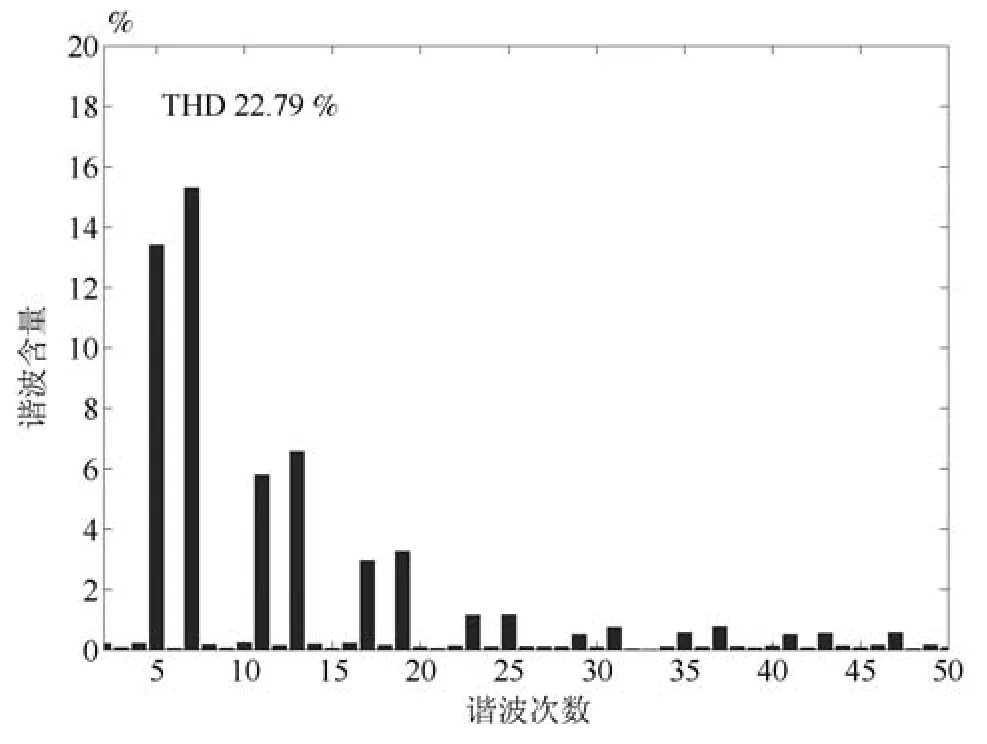
圖3　相電流頻譜(PI)Fig.3　Frequency spectrum of phase current(PI)

3.2　 大諧振增益下的PI-RES與APPI-RES電流控制對比仿真研究

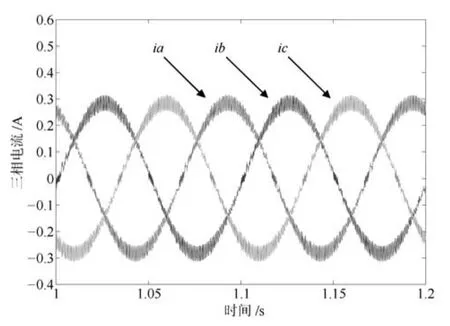
圖4　相電流(PI-RES)Fig.4　Phase currents(PI-RES)

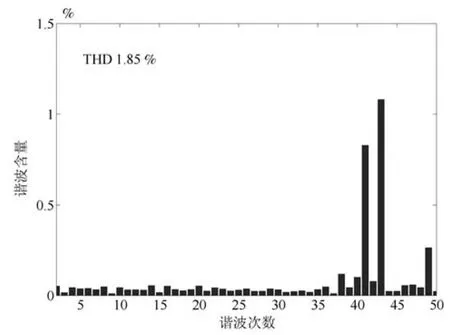
圖5　相電流頻譜(PI-RES)Fig.5　Frequency spectrum of phase current(PI-RES)

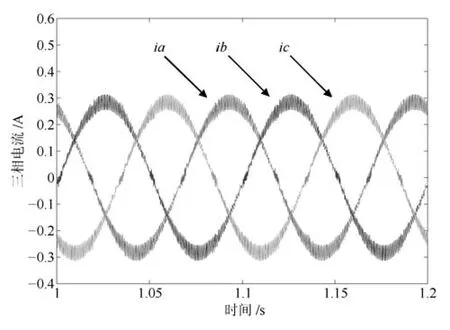
圖6　相電流(APPI-RES)Fig.6　Phase currents(APPI-RES)

級聯型PMSM 調速系統要求電流環響應速度遠快于速度環響應速度.為了更快、更準控制電機電流,需要增大電流環控制器增益系數.這里,PI-RES控制器的參數中kpc和kic取值與第3.1節相同,但取kresn=4000,n=1～6.PI-RES控制器中諧振器增益增大后,導致其輸出電壓振蕩,進而引起電流、電磁轉矩和轉速的振蕩,如圖8～11所示.為了驗證APPI-RES控制器對輸入延時的補償效果和大范圍參數不確定的魯棒性,增大APPI-RES控制器的諧振器增益并將電機電阻和電感設置為標稱值的3倍和2倍.由第2.1節分析知,所提參數自適應辨識算法需已知未知參數的界,這里假設系統未知參數 ?a、?b分別滿足:?a∈[?800,?50]、?b∈[50,500]. 所選未知參數的界應滿足:?a的界恒為負,?b的界恒為正.這里所選?a、?b的界只為驗證所提算法的有效性,即界的選取不唯一.APPI-RES控制器參數選為:式(13)中反饋增益陣G為對角陣,取G11=G22=15000,式 (20)中γ=25000,Γ6n為對角陣,取Γ6n11=Γ6n22=18000,式(40)中K為對角陣,取K11=K22=60.由圖12～14可見,當t=0.3s時負載由0.1Nm突變為0.2Nm,速度PI控制器級聯APPI-RES電流器的控制策略可有效抑制電壓擾動,消除諧波電流,實現了快速、準確的電流、轉矩和轉速控制.圖16為t時刻q軸電流控制誤差zq與t?D時刻zq的預測值zqp的仿真結果.可見,所提預測算法能夠實現漸近穩定的電流誤差預測.然而,在電機起動過程中,預測值與真實值符號相反,即控制器執行短時正反饋,這造成了起動過程中的短時電壓振蕩現象,如圖15所示.

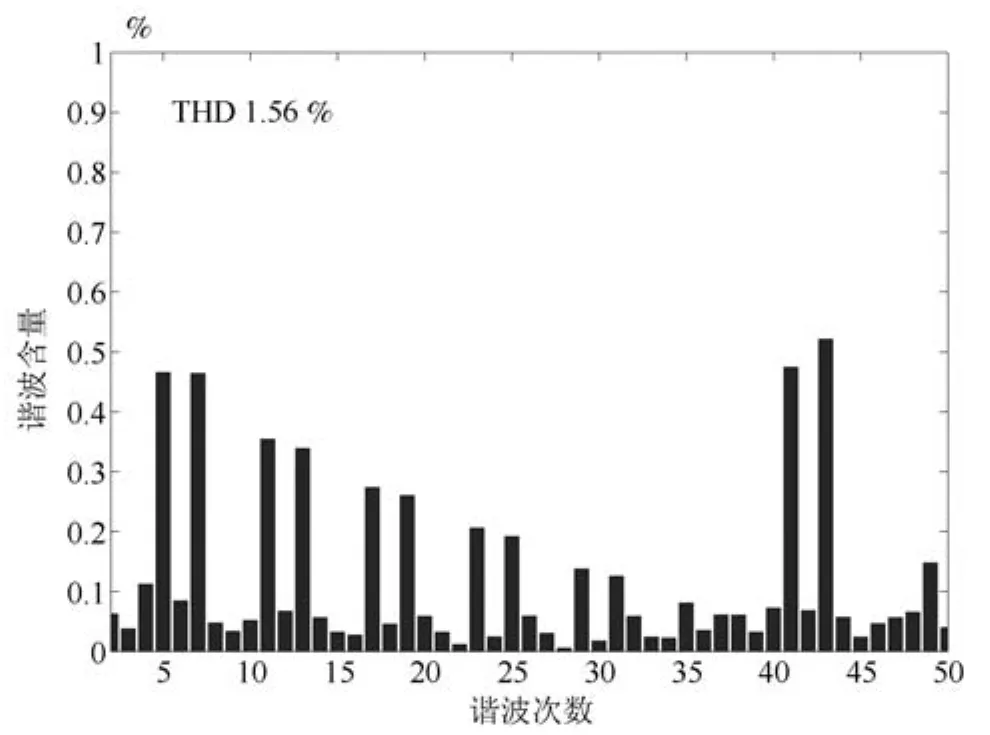
圖7　相電流頻譜(APPI-RES)Fig.7　Frequency spectrum of phase current(APPI-RES)

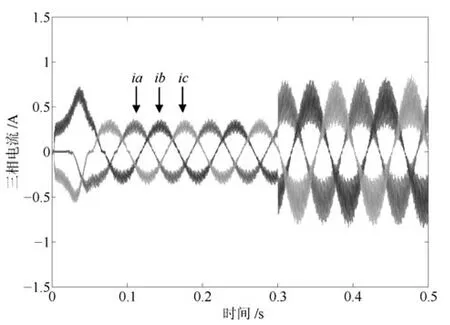
圖8　相電流(PI-RES)Fig.8　Phase currents(PI-RES)

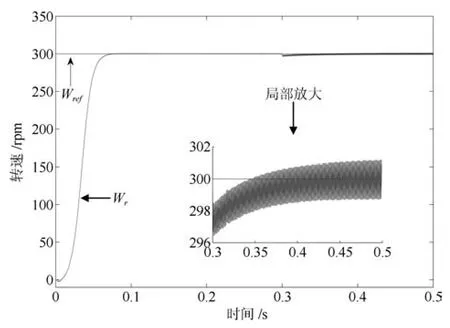
圖9　轉速(PI-RES)Fig.9　Speed(PI-RES)

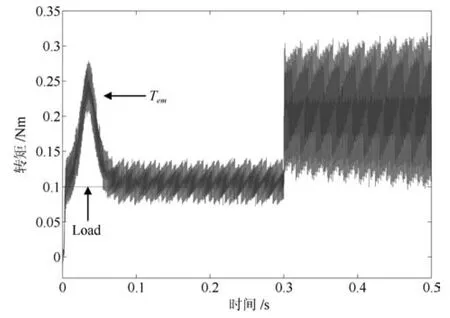
圖10　轉矩(PI-RES)Fig.10　Torque(PI-RES)

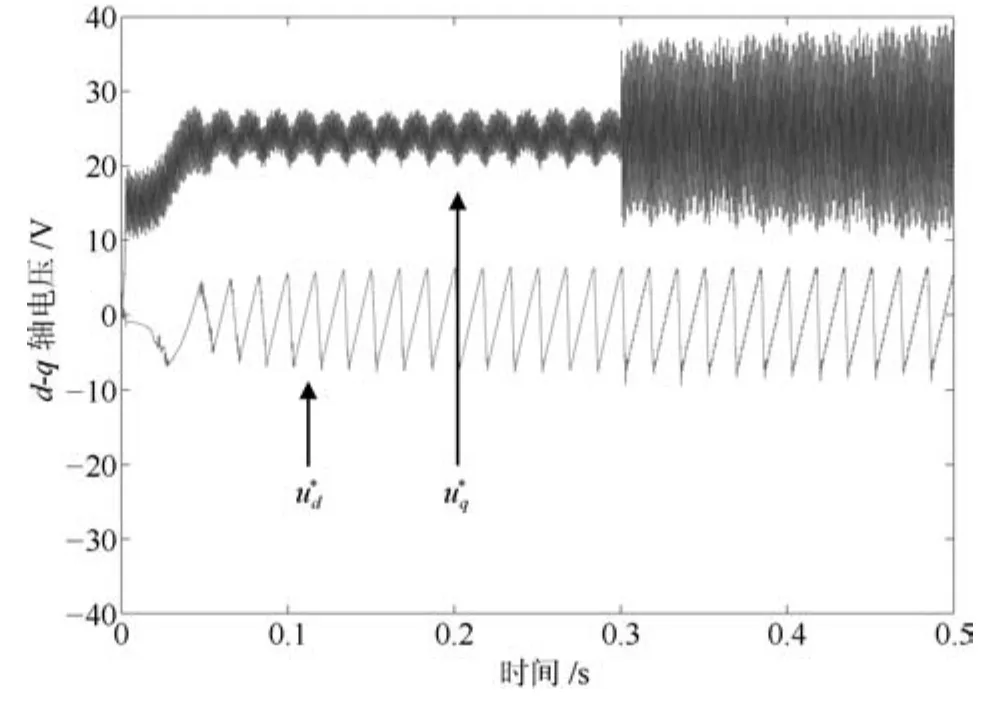
圖11d-q軸電壓(PI-RES)Fig.11　Voltages ofd-qaxises(PI-RES)

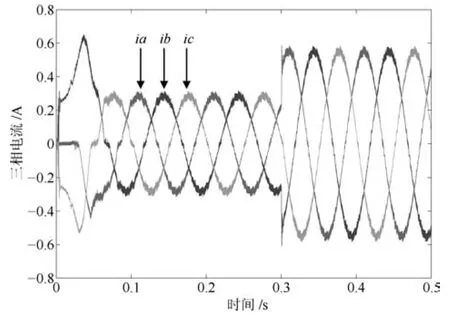
圖12　相電流(APPI-RES)Fig.12　Phase currents(APPI-RES)

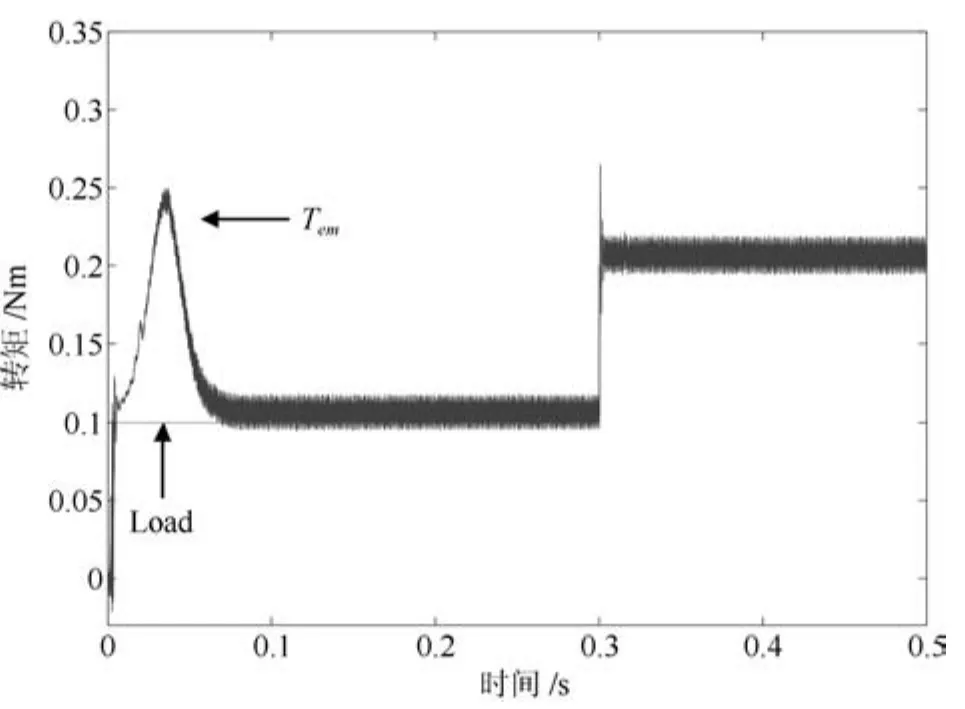
圖13　轉矩(APPI-RES)Fig.13　Torque(APPI-RES)

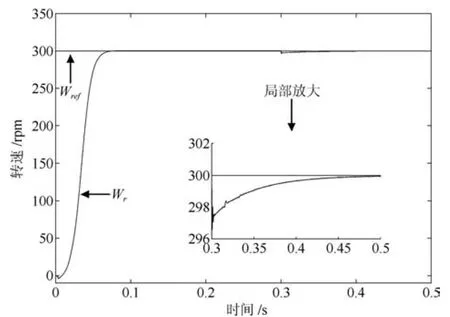
圖14　轉速(APPI-RES)Fig.14　Speed(APPI-RES)

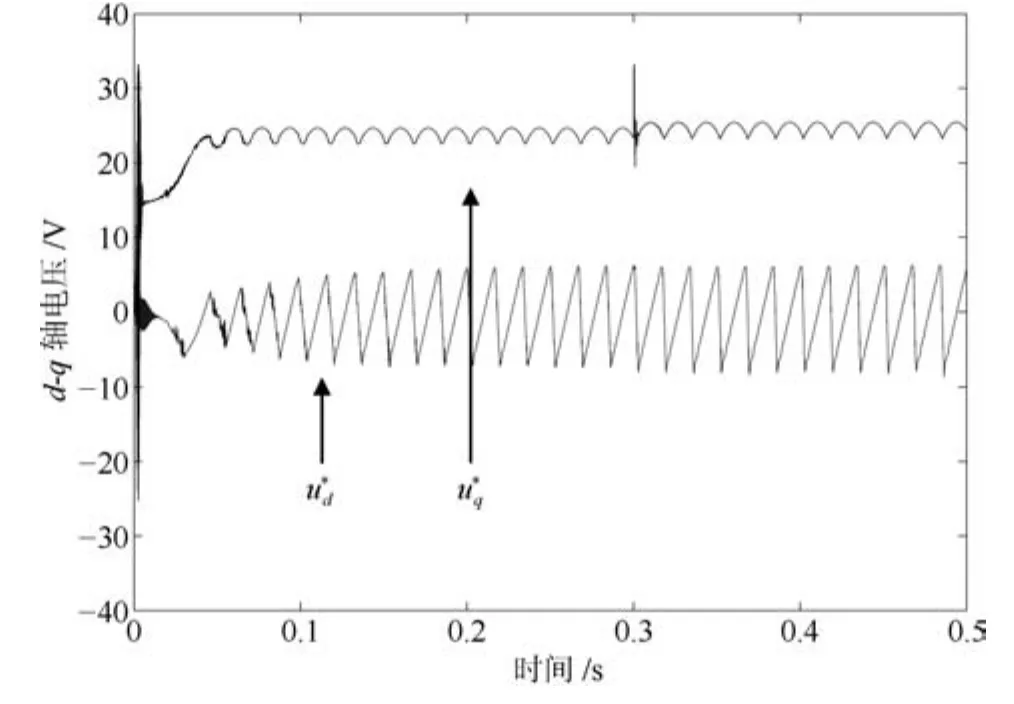
圖15d-q軸電壓(APPI-RES)Fig.15　Voltages ofd-qaxises(APPI-RES)

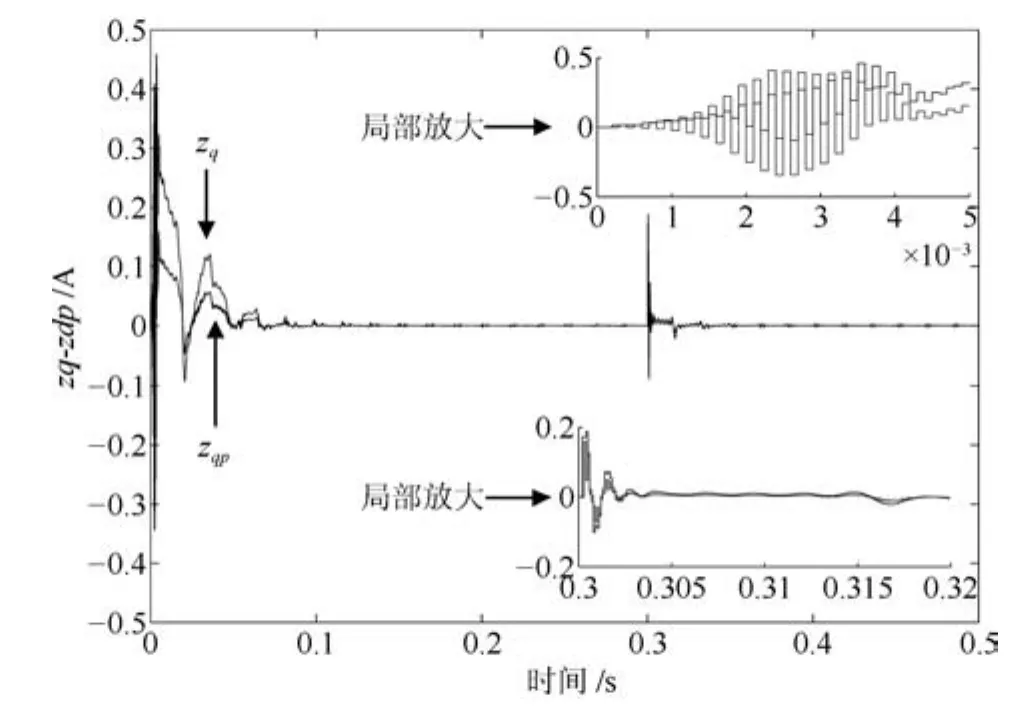
圖16q軸電流誤差及其預測值(APPI-RES)Fig.16　Current error and its predictive value ofqaxis(APPI-RES)

4　結論

1)在fs/fo工況下,PI-RES電流控制器受系統輸入延時的影響,將出現電流振蕩或不穩定現象.基于電流誤差系統狀態空間模型給出了常規PI-RES電流控制器設計方法,并分析了輸入延時降低解耦性能和使系統失穩的本質原因.

2)提出APPI-RES電流控制策略,實現對系統輸入延時的補償和擾動電壓的抑制.該方法可在系統參數未知的情況下觀測系統擾動和預測系統狀態.

3)所提方法是一種真正意義上的漸近穩定并聯型控制策略,實際應用中可通過電流控制精度和計算時間要求這種選擇并聯核函數的數量.

1 Chou M C,Liaw C M.Dynamic control and diagnostic friction estimation for an SPMSM-driven satellite reaction wheel.IEEE Transactions on Industrial Electronics,2011,42(10):4693?4707

2 Abdel-RadyY,MohamedI.Anewlydesigned instantaneous-torquecontrolofdirect-drivePMSM servoactuatorwithimprovedtorqueestimationand control characteristics.IEEE Transactions on Industrial Electronics,2007,54(5):2864?2873

3 EL-Refaie A M.Fractional-slot concentrated-windings synchronous permanent magnet machines:opportunities and challenges.IEEE Transactions on Industrial Electronics,2010,57(1):107?121

4 Jung J W,Leu V Q,Dot D,Kim E K,Choihh.Adaptive PID speed control design for permanent magnet synchronous motor drives.IEEE Transactions on Power Electronics,2015,30(2):900?908

5 Chang Sh,Chen P Y,Ting Yh,Hung S W.Robust current control-based sliding mode control with simple uncertainties estimation in permanent magnet synchronous motor drive systems.IET Electric Power Applications,2010,4(6):441?450

6 Niu Li,Yang Ming,Wang Geng,Xu Dian-Guo.Research on the robust current control algorithm of permanent magnet synchronous motor based on deadbeat control principle.Proceedings of the CSEE,2013,33(15):78?85(牛里,楊明,王庚,徐殿國.基于無差拍控制的永磁同步電機魯棒電流控制算法研究.中國電機工程學報,2013,33(15):78?85)

7 Errouissi R,Ouhrouche M,Chen Wh,Trzynadlowski A.Robust nonlinear predictive controller for permanentmagnet synchronous motors with an optimized cost function.IEEE Transactions on Industrial Electronics,2012,59(7):2849?2858

8 Kong Xiao-Bing,Liu Xiang-Jie.Efficient nonlinear model predictive control for permanent magnet synchronous motor.Acta Automatica Sinica,2014,40(9):1958?1966(孔小兵,劉向杰.永磁同步電機高效非線性模型預測控制.自動化學報,2014,40(9):1958?1966)

9 Wang En-De,Huang Sheng-Hua.Current Regulator design for surface permanent magnet synchronous motor servo systems.Proceedings of the CSEE,2012,32(33):82?88(王恩德,黃聲華.表貼式永磁同步電機伺服系統電流環設計.中國電機工程學報,2012,32(33):82?88)

10 EscobarG,Hernandez-BrionesPG,MartinezPR,Hernandez-Gomez M,Torres-Olguin R E.A repetitive-based controller for the compensation of 6l±1 harmonic components.IEEE Transactions on Industrial Electronics,2008,55(8):3150?3158

11 Kuang Min-Chi,Zhu Ji-Hong,Ji Jing-Hua.Phase current distortion correction control for aerospace fuel pump motor.Control and Decision,2015,30(5):899?904(匡敏馳,朱紀洪,吉敬華.航空油泵電機的相電流畸變糾正控制.控制與決策,2015,30(5):899?904)

12 Li Yi-Tuo,Lu Hai-Feng,Qu Wen-Long,Sheng Shuang.A permanent magnet synchronous motor current suppression method based on resonant controllers.Proceedings of the CSEE,2014,34(3):423?430(李毅拓,陸海峰,瞿文龍,盛爽.基于諧振調節器的永磁同步電機電流諧波抑制方法.中國電機工程學報,2014,34(3):423?430)

13 McGrath B P,Parker S G,Holmes D G.High-performance current regulation for low-pulse-ratio inverters.IEEE Transactions on Industry Applications,2013,49(1):149?158

14 Vidal A,Freijedo F D,Yepes A G,Fernandez-Comesana P,Malvar J,Lopez O,Doval-Gandoy J.Assessment and optimization of the transient response of proportional-resonant current controllers for distributed power generation systems.IEEE Transactions on Industrial Electronics,2013,60(4):1367?1383

15 Yim J S,Sul S K,Bae Bh,Patel N R,Hiti S.Modi fi ed current control schemes for high-performance permanentmagnet ac drives with low sampling to operating frequency ratio.IEEE Transactions on Industry Applications,2009,45(2):763?771

16 Yepes A G,Vidal A,Malvar J,L′opez O,Doval-Gandoy J.Tuning method aimed at optimized settling time and overshoot for synchronous proportional-integral current control in electric machines.IEEE Transactions on Power Electronics,2014,29(6):3041?3054

17 Franklin G F,Powell J D,Emami-Naeini A[Author],Zhu Qi-Dan,Zhang Li-Ke,Yuan Xin[Translator].Feedback Control of Dynamic Systems(Fourth Edition).Beijing:Publishing House of Electronics Industry,2004.401?408(Franklin G F,Powell J D,Emami-Naeini A[著],朱齊丹,張麗珂,原新[譯].動態系統的反饋控制.第4版.北京:電子工業出版社,2004.401?408)

18 L′echapp′e V,Moulay E,Plestan F,Glumineau A,Chriette A.New predictive scheme for the control of LTI systems with input delay and unknown disturbances.Automatica,2014,52:179?184