聯合相鄰幀預測的心臟磁共振電影成像方法

董家林　洪明堅　張海標　葛永新

磁共振成像(Magnetic resonance imaging,MRI)作為一種醫學成像手段,以其良好的軟組織成像、細致的圖像顆粒度、較高的空間分辨率以及無創的特性廣泛應用于醫學領域.然而,由于MRI的掃描時間比較長,患者在成像期間會產生自主或非自主的運動,導致圖像失真,從而影響了醫生診斷,限制了MRI在臨床醫學中的應用.動態磁共振成像(Dynamic MRI)主要用于捕捉組織器官的動態變化或運動過程,對成像速度的要求更高,因此加快成像速度尤其重要.

受MRI掃描儀采集速度的限制,一般通過減少采樣量以縮短掃描時間,再從下采樣的數據中重建出高分辨率的圖像.壓縮感知(Compressed sensing,CS)[1?4]理論表明,只要圖像在某個變換域是稀疏的,通過隨機下采樣就能從少量的下采樣數據中重建出高質量的圖像.由于CS理論突破了傳統Nyquist采樣定理的瓶頸,目前已在雷達成像[5]、紅外成像[6]、磁共振成像[7]等領域得到廣泛的應用.CS理論應用條件主要包括信號具有稀疏表示、不相干的(Incoherent)采樣以及有效的非線性重建算法三個方面[8?9].常用的稀疏變換有傅里葉變換(Fourier transform,FT)和小波變換等[10?11].近年來,基于分塊的自適應稀疏表示也得到了廣泛應用[12?15].

動態磁共振成像序列不僅在空間上具有一定的稀疏特性,而且在時間上也存在較大冗余[16].因此,如何有效利用動態磁共振成像在時間域上的冗余特性,是CS理論運用于動態磁共振成像的關鍵.常見的基于CS理論的動態磁共振成像方法有 k-t SPARSE[17]、k-t FOCUSS[18]、k-t FOCUSS ME/MC[19]和MASTeR[20]等.k-t SPARSE利用動態磁共振成像在空間域和時間域冗余的特性,采用小波變換作為圖像序列在空間域的稀疏約束,同時加入沿時間軸的傅里葉變換作為圖像序列在時間域的稀疏約束,建立CS成像模型重建圖像序列.然而k-t SPARSE求解過程采用非線性共軛梯度算法[21],求解時計算量大,且收斂緩慢、求解時間較長.k-t FOCUSS利用了動態磁共振成像在時間域的冗余,采用沿時間軸的傅里葉變換作為稀疏約束構建成像模型,并利用沿時間軸的平均圖像作為每一幀圖像的預測圖像,最后通過FOCUSS[22]方法重建圖像差.然而,k-t FOCUSS采用沿時間軸的平均圖像對圖像序列進行預測,只能較為準確地估計少部分圖像,無法保證大多數時間節點上的預測效果[23].為了克服k-t FOCUSS的這一不足,k-t FOCUSS ME/MC建議使用一幀或兩幀全采樣的圖像作為參考圖像,再利用塊匹配算法[24]計算參考圖像與目標圖像之間的運動估計,提升了預測圖像的準確性.然而,在沒有全采樣參考圖像時,該方法仍然采用沿時間軸的平均圖像作為參考圖像,而這樣的選擇在影響運動估計效果的同時,也降低了重建圖像的質量.MASTeR方法通過計算相鄰前后兩幀圖像之間的運動量,估計出預測圖像,并利用預測圖像與目標圖像差的稀疏性,建立具有兩個稀疏約束的成像模型.具體來說,該方法計算出前一幀與當前幀的運動估計,得到前向預測圖像,同時計算出后一幀與當前幀的運動估計,得到后向預測圖像,并分別以前、后向預測圖像與目標圖像的差作為稀疏約束建立成像模型.

本文提出了一種新的聯合相鄰幀預測(Joint adjacent-frame prediction,JAFP),根據動態磁共振成像序列相鄰前后幀之間較高的相似性,分別求解相鄰前后幀之間的運動估計,聯合預測中間幀圖像.同時,利用目標圖像序列與預測圖像序列的圖像差在時間上的擬周期性,增加圖像差在時間軸的稀疏約束,建立基于壓縮感知的成像模型.JAFP方法從以下兩個方面提升了動態磁共振圖像序列的稀疏表示:1)聯合相鄰前后兩幀運動估計所得圖像的預測效果優于前一幀向后運動估計的圖像或后一幀向前運動估計的圖像,因此計算所得的圖像差更為稀疏;2)在時間域增加稀疏變換,進一步稀疏了圖像差信號.實驗結果表明,該方法有效提升了動態圖像序列的稀疏度,顯著改進了重建圖像的質量.

1　成像模型

1.1　稀疏動態成像模型

在動態磁共振成像中,利用動態磁共振圖像在時空域的冗余性,建立基于壓縮感知理論的成像模型.

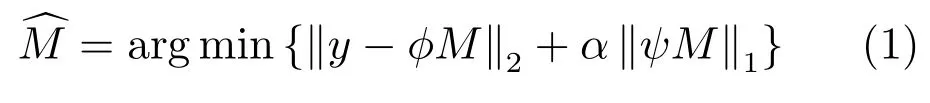
其中,M∈Cn×p×t為t幀、n×p大小的圖像,y為下采樣的k空間數據,φ為下采樣傅里葉變換,ψ為稀疏變換.根據壓縮感知理論,在同等采樣量的情況下,越稀疏的表示,圖像重建質量越高[7].

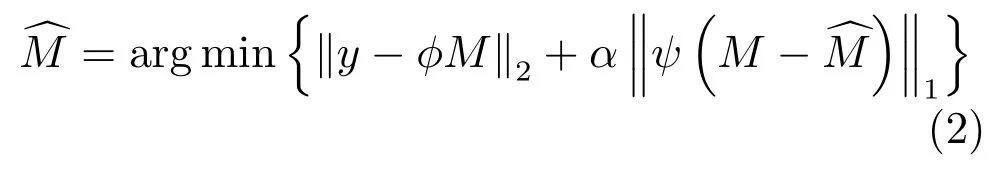
為了獲得更稀疏的表示,k-t SPARSE選擇空間域的小波變換和時間域的傅里葉變換作為稀疏變換.而k-t FOCUSS,k-t FOCUSS ME/MC,MASTeR等方法則將目標圖像與預測圖像的差作為成像序列在空間域的稀疏約束建立成像模型如下:其中,為預測圖像.在k-t FOCUSS中,選擇沿時間軸的平均圖像,對心臟成像時,由于心臟跳動的擬周期性,取ψ為沿時間軸的傅里葉變換,以獲得最稀疏的表示;k-t FOCUSS ME/MC改進了k-t FOCUSS中預測圖像的計算方法,通過塊匹配算法計算沿時間軸的平均圖像與目標圖像之間的運動估計,并求得;MASTeR把分成前向F和后向B兩部分,前向F通過計算前一幀與當前幀的運動估計獲得,后向B通過計算后一幀與當前幀的運動估計獲得,最后用兩個稀疏約束‖M?f‖1和‖M?B‖1構建成像模型.

1.2　聯合相鄰幀預測方法

相鄰幀圖像即為當前幀圖像的前一幀圖像或后一幀圖像.由于它們與當前幀的掃描時間間隔較短,因此相鄰幀圖像往往差別較小,如圖1所示.其中,從左至右為第4～6、12～14幀圖像的感興趣區域(Region of interest,ROI),差別非常小,肉眼難以辨別,但從其與第5幀圖像ROI的誤差,可以直觀地看出相鄰幀圖像與非相鄰幀圖像之間的差異.在對當前幀圖像進行預測時,便可以采用當前幀的前一幀圖像或者后一幀圖像對當前幀圖像進行預測[25].圖2用結構相似性(Structural similarity,SSIM)[26]比較了各幀之間的相似度.

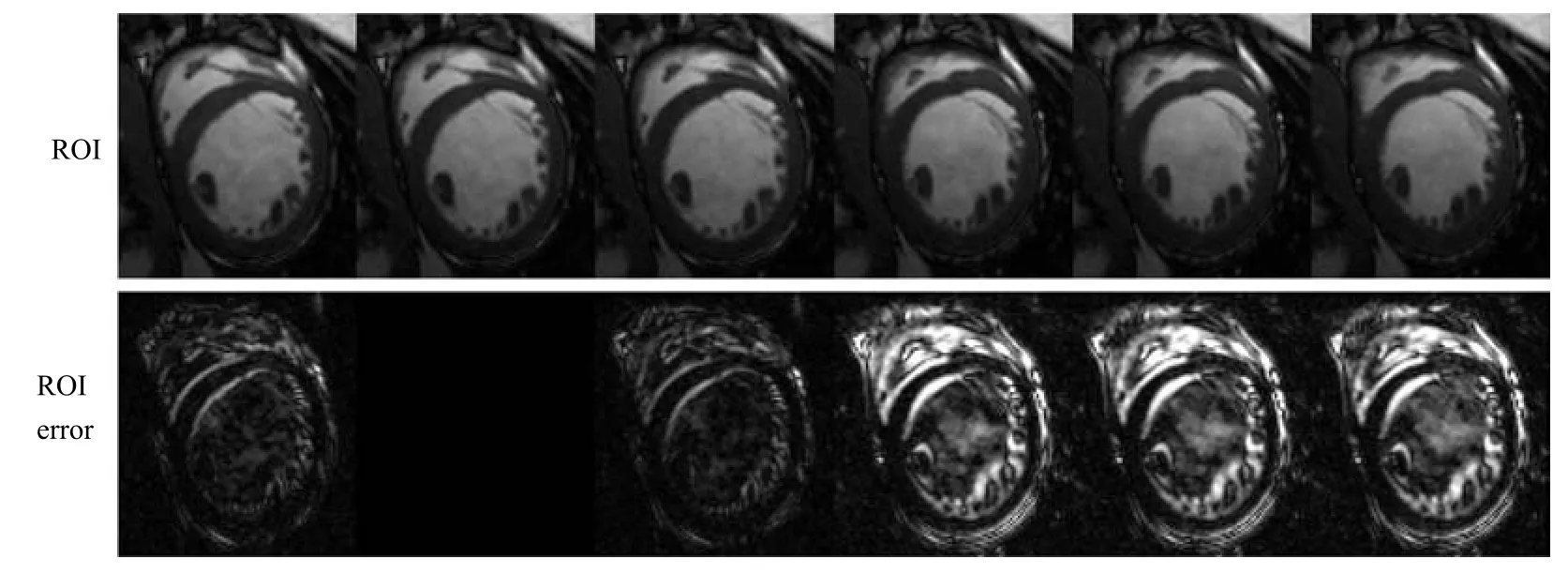
圖1　相鄰幀圖像與非相鄰幀圖像之間的差異Fig.1　The difference of between adjacent frame and non-adjacent frame

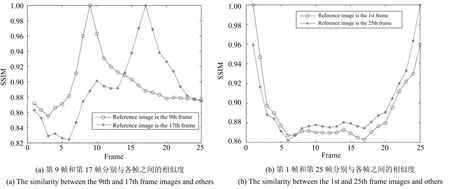
圖2　幀間相似度Fig.2　The similarity

由于相鄰幀之間的差異較小,因此選擇相鄰前后兩幀運動估計后的圖像預測效果更優.記前向運動估計算子為F,后向運動估計算子為B,則前向運動估計后的第i幀預測圖像F(i)和后向運動估計后的的第i幀預測圖像B(i)可表示為

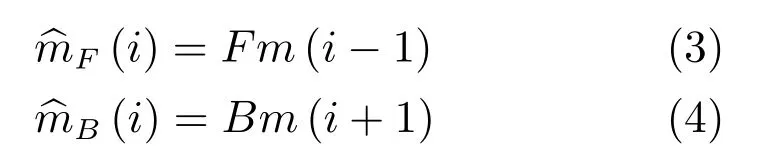
其中,m(i)表示成像序列的第i幀圖像,由于運動估計后的預測圖像和本真圖像之間存在差異,記u(i)為前向運動估計后的預測圖像序列與本真圖像序列的差函數,v(i)為后向運動估計后的預測圖像序列與本真圖像序列的差函數,則有

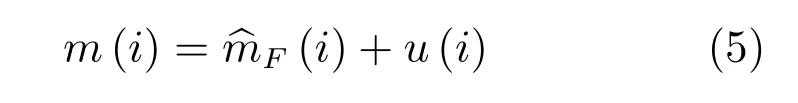
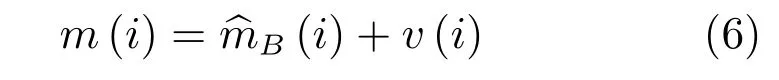
結合式(5)和式(6)可得

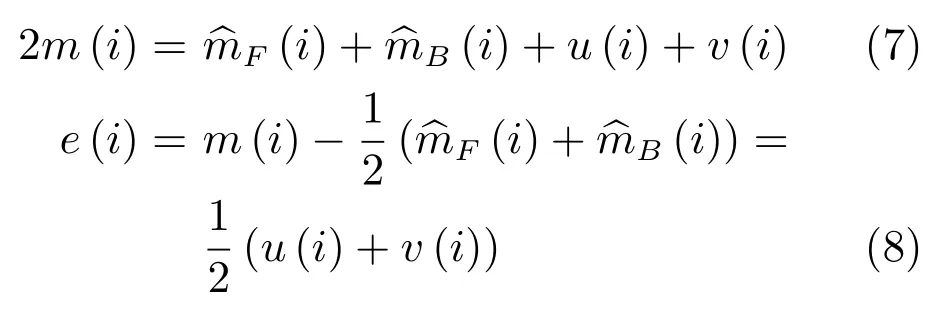
其中,e(i)為聯合前后幀運動估計后的預測圖與本真圖像的差.然而,第一幀圖像和最后一幀圖像只有一個相鄰幀.由于心臟跳動是擬周期的,如圖2(b)所示,因此可以通過周期延拓進行邊界處理.因此,有

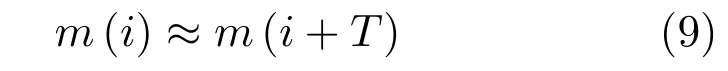
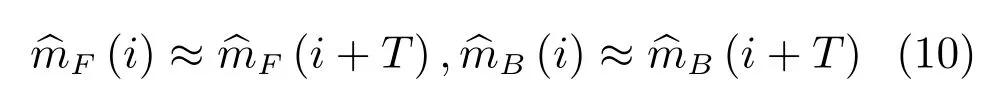
結合式(8)不難看出,其圖像差e(i)在時間域上仍然是擬周期的.

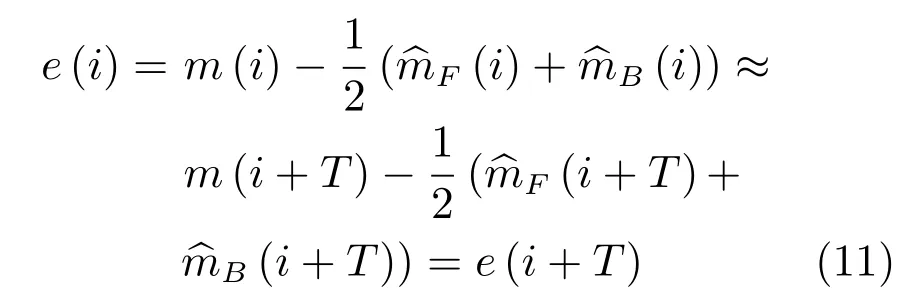
由此可知,圖像差序列在傅里葉變換域上是稀疏的.因此,增加沿時間軸的傅里葉變換,更有利于重建質量的提升.

1.3　成像模型

本文提出的成像方法JAFP在聯合相鄰幀預測的同時,增加時間域上的稀疏變換,獲得更稀疏的圖像差表示,以提升重建質量.根據式(2)和式(8)可得JAFP的成像模型如下:

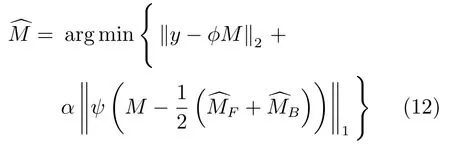
其中,ψ為沿時間軸的傅里葉變換,F表示前向運動估計后的預測圖像序列,B表示后向運動估計后的預測圖像序列.運動估計算子F和B是通過計算初始圖像序列相鄰前后幀圖像的運動估計所得.

k-t FOCUSS ME/MC和MASTeR在模型上都利用了圖像差作為成像序列在空間域上的稀疏約束,然而,在沒有全采樣參考圖像時,k-t FOCUSS ME/MC采用的沿時間軸平均圖像作為參考圖像,盡管其利用了圖像差序列在時間上的冗余進一步稀疏了圖像差序列,但其質量較差的參考圖像影響了運動估計的結果,限制了重建圖像質量的進一步提升.而MASTeR選用相鄰幀圖像的運動估計預測當前幀圖像,在預測準確性上優于k-t FOCUSS ME/MC,然而MASTeR忽略了圖像差序列在時間上的冗余.而本文提出的成像模型在綜合二者優勢的同時,采用聯合相鄰幀預測的方式進一步提升了預測效果.

1)JAFP與MASTeR類似地都利用了相鄰幀圖像的運動估計,但JAFP聯合相鄰前后兩幀圖像計算所得的運動估計,替代MASTeR所用的單幀運動估計.從模型上看,MASTeR的稀疏約束為

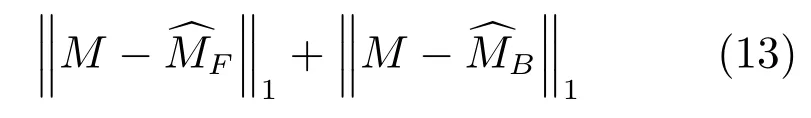
而JAFP的稀疏約束為

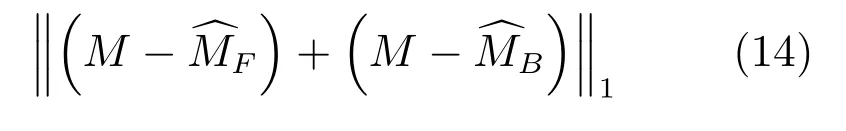
顯然,根據1范數的性質[27]

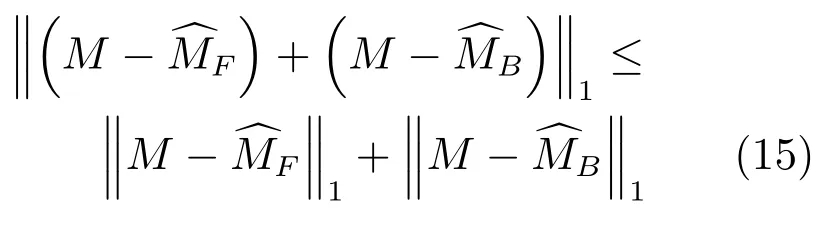
JAFP具有更優的稀疏表示.

2)JAFP利用目標圖像與預測圖像的圖像差在時間軸上的擬周期性(由式(11)可知)增加時間軸的稀疏約束ψ,進一步提升了稀疏性,彌補了MASTeR的不足.

2　重建算法

JAFP成像方法通過初始圖像序列計算相鄰前后幀圖像的運動估計算子求得前向預測圖像序列和后向預測圖像序列,進而計算預測圖像序列與目標圖像序列的圖像差,建立CS成像模型完成重建.重建完成后,可以用重建所得結果更替初始圖像序列,再次運用JAFP方法完成重建.該過程可迭代多次,隨著迭代次數的增加,被更替的預測圖像序列愈加接近目標圖像,使得求解目標(圖像差)愈稀疏,有利于提升下一次迭代的圖像質量,當圖像質量的改進小于閾值時,迭代停止.

算法流程如下:

步驟1.初始化:根據CS理論,從下采樣k空間中重建獲得初始圖像序列,即根據式(1)求得后,令k=1,M0=;

步驟2.運動估計:使用重建的圖像序列Mk?1估計相鄰幀之間的運動,利用復小波變換(Complex wavelet transform,CWT)運動估計方法,求得運動估計算子F和B;

步驟3.運動補償:利用圖像差稀疏這一特性建立新CS成像模型

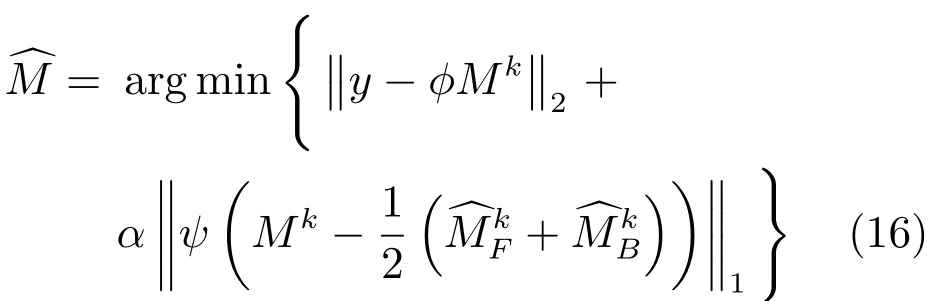
步驟 4.如果‖?Mk‖/‖Mk‖≤ε,則停止迭代,輸出.否則,令Mk=,k=k+1,重復步驟2.

算法流程圖如圖3所示.

3　實驗方法

3.1　數據集

數據集1[18]:該數據集為k-t FOCUSS實驗過程所用數據集,系利用飛利浦1.5T磁共振掃描儀采集得到一名病人的心臟電影成像數據,包括25幀全采樣k空間數據,視場(Field of view,FOV)大小為306.0mm×260.00mm,掃描矩陣為220像素×256像素,采集順序為平衡穩態自由進動(Balance steady state free precession,bSSFP),傾角50°,TR=3.45ms,心臟跳動頻率75bpm.數據集包括心臟舒張和收縮兩個階段.

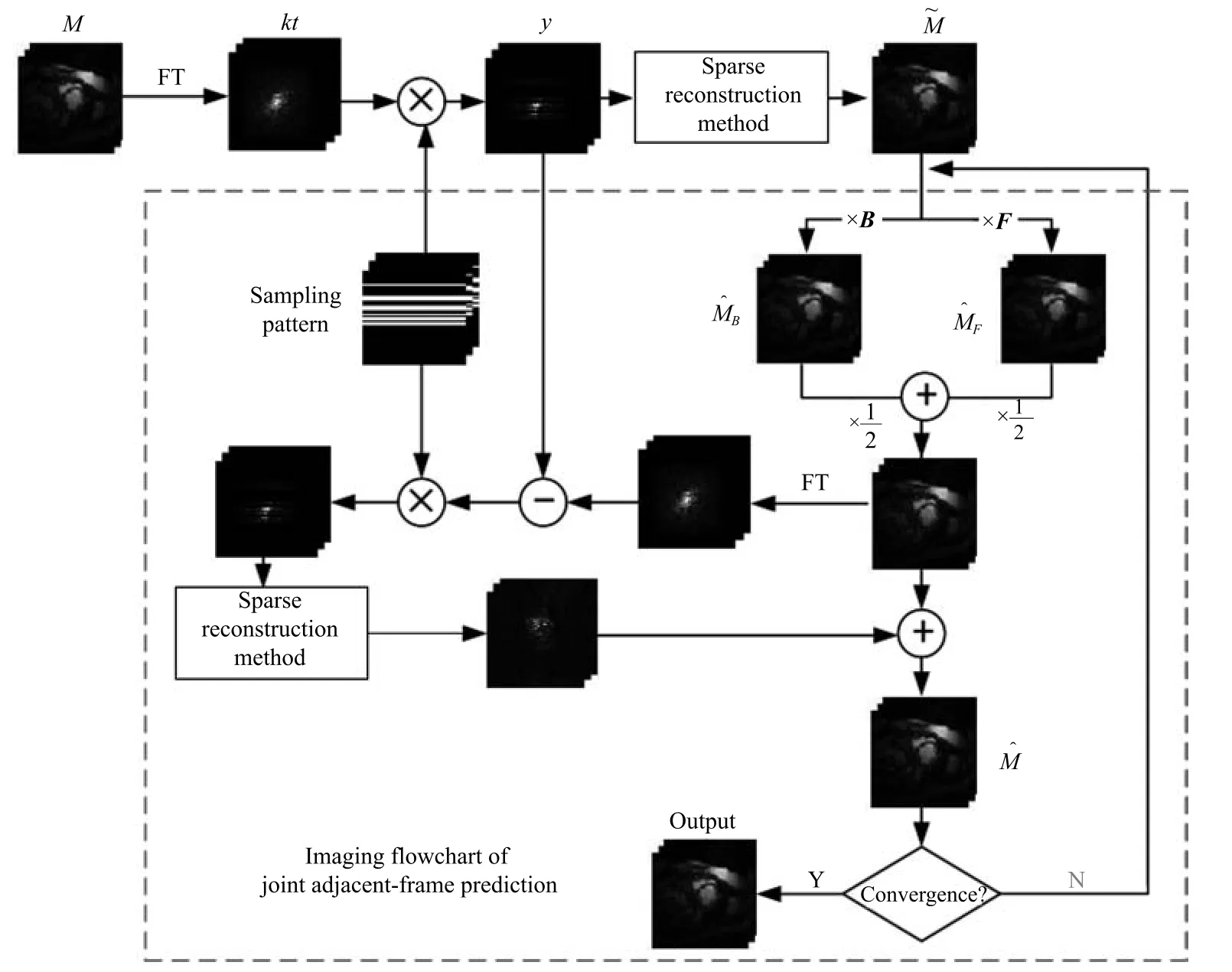
圖3　算法流程圖Fig.3　Algorithm fl ow chart

數據集2:該心臟電影數據共25幀,利用飛利浦1.5T磁共振掃描儀采集獲得一名自愿者的心臟電影成像數據,FOV為345.00mm×270.00mm,掃描矩陣為256像素×256像素.數據是使用穩態自由進動(SSFP)順序的方式獲得,穩態自由進動過程傾角為50°,TR=3.45ms,心臟跳動頻率66bpm.數據集包括心臟舒張和收縮兩個階段.

3.2　采樣模式

由于k空間中低頻區域即中心部分能量較大,高頻區域能量較低,低頻區域數據包含圖像的對比度和信噪比,高頻區域數據包含圖像的邊緣和細節等特征[28].因此采樣時盡可能多地采集低頻區域數據,其他區域在采樣時盡可能保證隨機.在保證圖像一定信噪比的同時,也滿足CS理論中不相干(Incoherent)采樣的要求.

實驗主要采用笛卡爾下采樣模式,k空間中心的8行數據全采樣以保證重建圖像的信噪比,余下k空間數據通過標準高斯分布隨機采集獲得.盡管在實驗過程中選擇了笛卡爾采樣,但該算法并不限定采樣模式.

3.3　求解方法

利用NESTA[29]算法求解式(1)獲得初始圖像,算子F和B可通過運動估計方法求解.常用的運動估計方法包括塊匹配算法(Overlapped block motion compensation,OBMC)、復小波變換(CWT)[30]和光流法(Optical fl ow,OP)[31]等,其中OBMC和OP一般不適宜于處理包含噪聲或低信噪比的動態圖像序列[32],而JAFP算法是一個迭代收斂的過程,初始圖像序列往往有較大的噪聲,因此選擇能抑制噪聲影響的CWT運動估計方法.

由于心臟圖像差在時間域是擬周期的,因此稀疏變換Ψ選擇沿時間軸的傅里葉逆變換.然后,再次利用NESTA算法求解式(16),求解出^M后,更新F和B,并重復該過程,直至收斂.

3.4　實驗結果的評估方法

為了更好地對比實驗的重建效果,通過計算原動態磁共振成像數據集與下采樣情況下的重建圖像數據的差別定量分析重建的效果.結構相似性(SSIM)的值可以更好地反映人眼的主觀感受[33],因此計算每一幀重建圖像與本真圖像的結構相似性評估重建結果的優劣.

SSIM的計算公式如下:

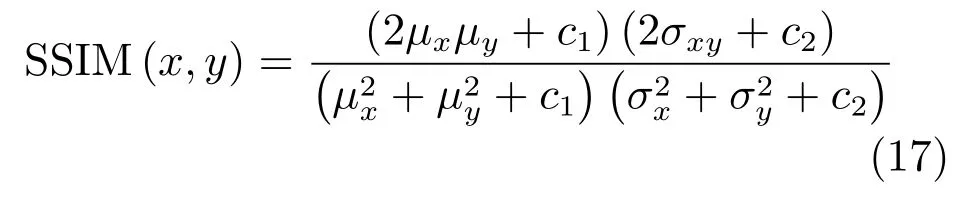
其中,x,y分別為兩幅圖像,μx表示x的平均值,表示x的方差,σxy表示x與y的協方差,c1=(k1L),c2=(k2L),L為像素值的動態范圍,k1取0.01,k2取0.03.

同時,高頻誤差范數 (High-frequency error norm,HFEN)[34]能夠評估重建圖像邊緣和細節特征的質量.因此,計算原動態磁共振成像數據集與下采樣重建圖像數據集的高頻誤差范數(HFEN)定量分析重建結果的質量.

HFEN的計算公式如下:

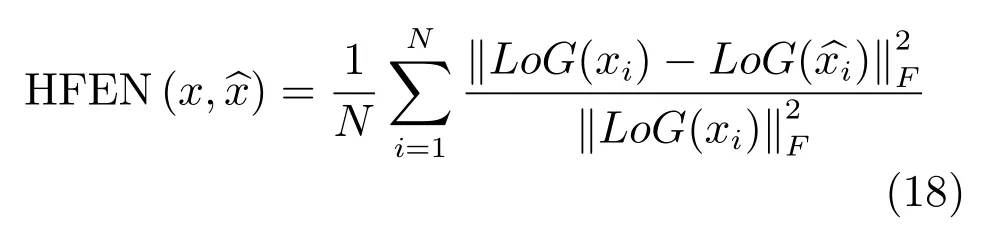
其中,LoG(x)為拉普拉斯高斯濾波函數,模版尺寸15,濾波器標準差為1.5.

4　實驗結果及分析

4.1　數據集1的實驗結果及分析

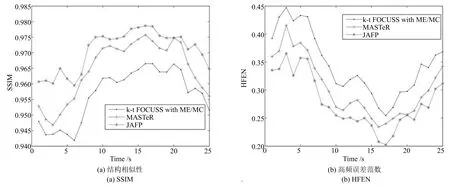
圖4　數據集1在4倍下采樣時重建質量比較Fig.4　The comparison of reconstruction quality with acceleration factor of 4 for dataset 1

圖4(a)和圖5(a)分別展示了數據集1在4倍下采樣和8倍下采樣時,三種重建方法重建后每一幀圖像感興趣區域(ROI)的SSIM對比圖.圖4(b)和圖5(b)分別展示了ROI的HFEN對比圖.由于JAFP方法進一步提升了預測心臟運動信息的準確性,其重建結果在SSIM和HFEN兩項評價指標上均超越MASTeR和k-t FOCUSS ME/MC.同時,實驗選取了兩個心臟壁區域(圖6(a)和圖7(a)方框標注所示),進而比較了各重建方法重建該區域的平均灰度變化,具體如圖6和圖7所示.根據圖中所示重建結果與真實結果的誤差絕對值可知,基于JAFP方法的重建結果在8倍下采樣時收縮過程的灰度變化總體上也優于MASTeR和k-t FOCUSS ME/MC.

圖8呈現了數據集1在4倍下采樣和8倍下采樣時三種重建方法重建的ROI及其誤差圖,圖中選取了三幀圖像,分別為心臟收縮階段的第4幀、收縮完全的第9幀以及舒張階段的第18幀.圖9比較了各重建方法重建的變化較明顯且靠近心臟壁位置(原成像序列的第130列和第160列)的截面及其誤差.由于JAFP在綜合MASTeR和k-t FOCUSS ME/MC優勢的同時,還聯合相鄰幀預測進一步提升了預測的準確性,其重建的ROI誤差以及截面誤差都明顯少于MASTeR和k-t FOCUSS ME/MC.

與此同時,定量分析在不同加速倍數下k-t FOCUSS ME/MC、MASTeR和JAFP三種方法重建的圖像序列的重建效果,計算了在2,4,8,10,16倍加速倍數下共25幀圖像序列在SSIM和HFEN兩項評價指標上的均值和方差,如圖10所示.從圖中不難看出,JAFP重建方法在各加速倍數下,重建結果的SSIM以及HFEN兩項評價指標均優于k-t FOCUSS ME/MC和MASTeR.由于JAFP利用相鄰幀之間的運動估計,聯合預測中間幀圖像,提升了預測效果,同時,時間域稀疏約束的增加,使得其重建結果在更高倍的下采樣時重建效果提升明顯.

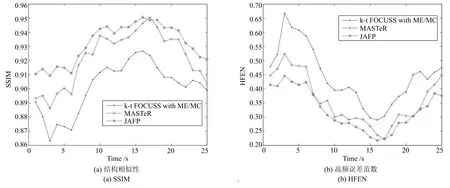
圖5　數據集1在8倍下采樣時重建質量比較Fig.5　The comparison of reconstruction quality with acceleration factor of 8 for dataset 1

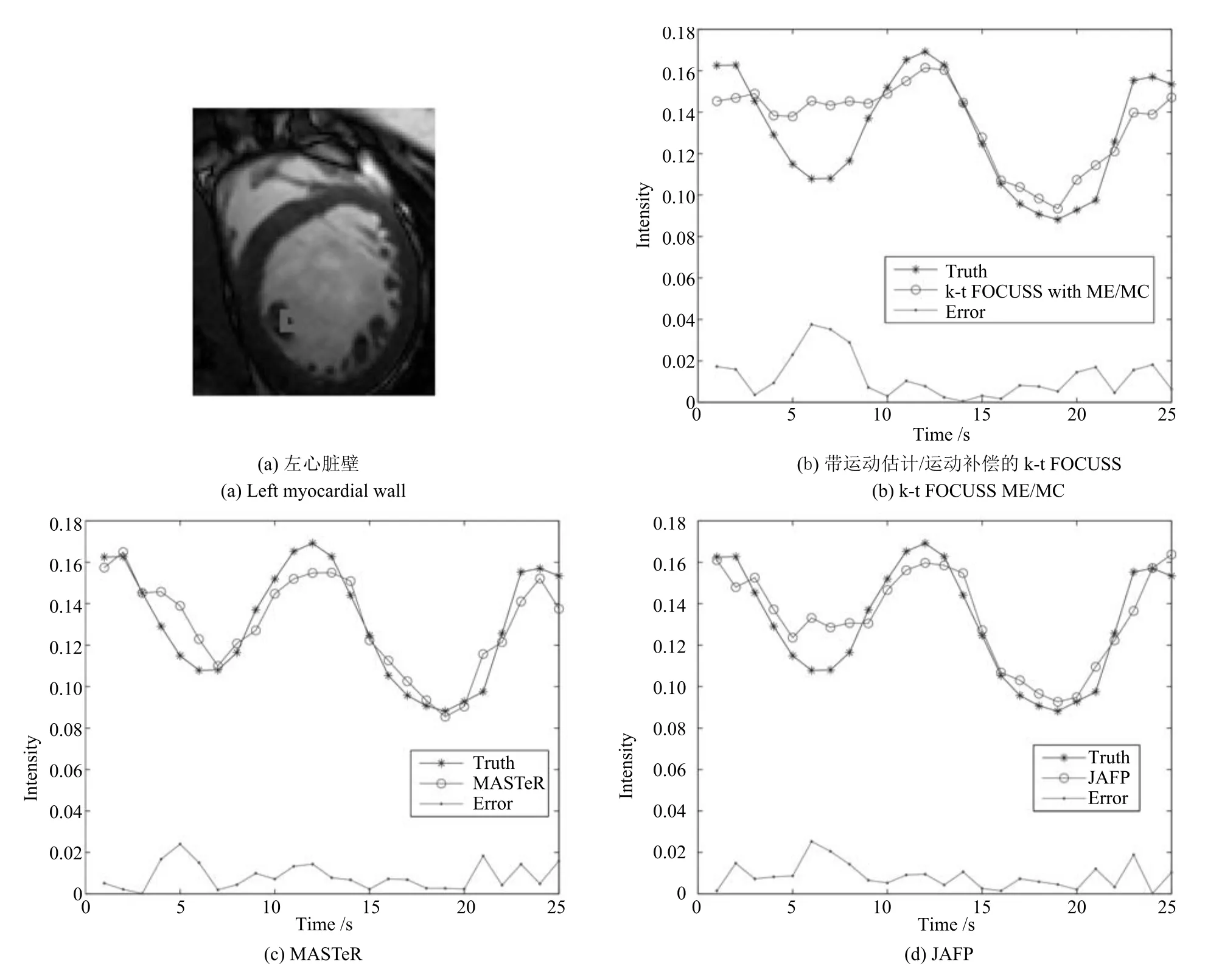
圖6　數據集1在8倍下采樣時左心臟壁灰度均值的比較Fig.6　The comparison of reconstructed gray average values and errors with acceleration factor of 8 for left myocardial wall of dataset 1

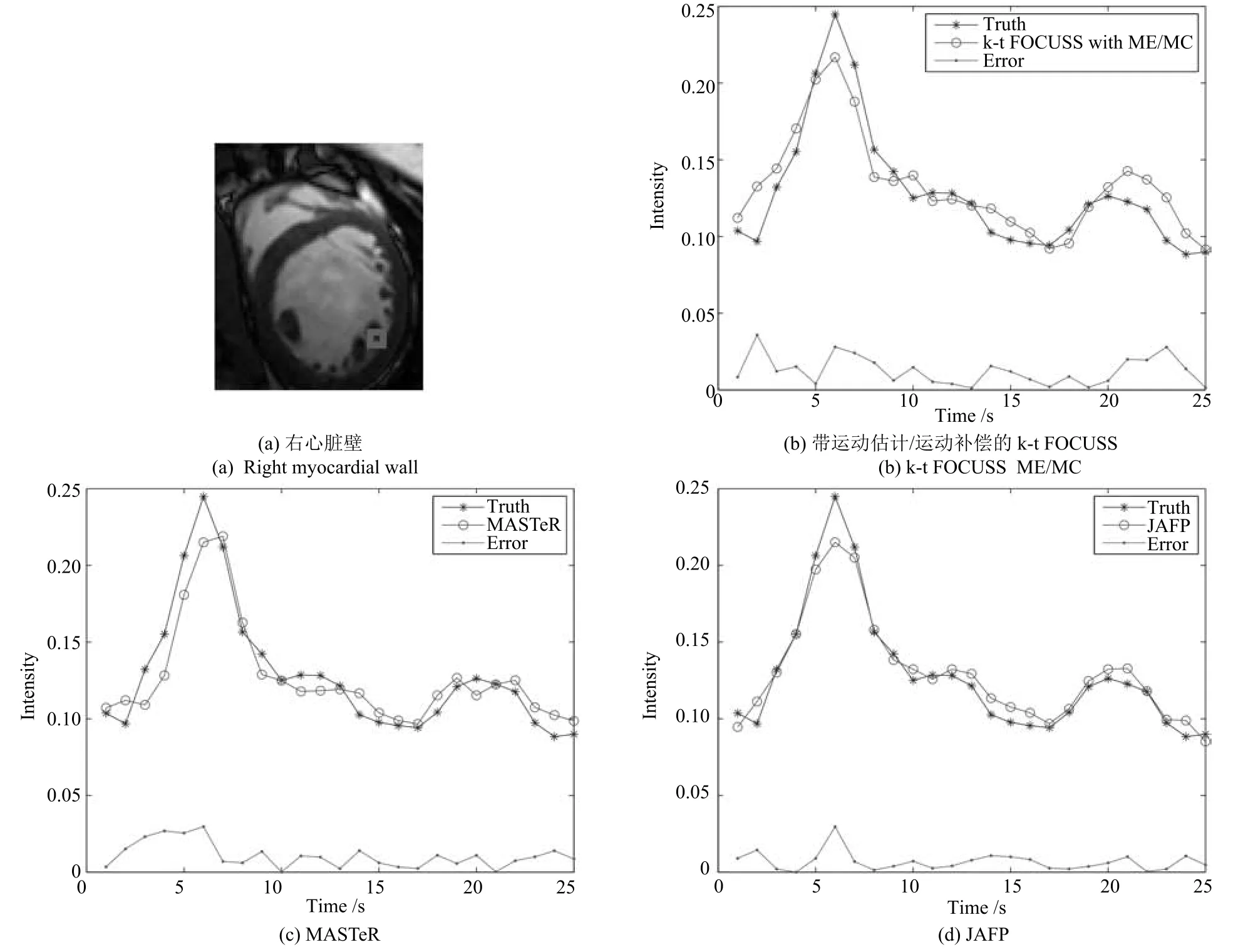
圖7　數據集1在8倍下采樣時右心臟壁灰度均值的比較Fig.7　The comparison of reconstructed gray average values and errors with acceleration factor of 8 for right myocardial wall of dataset 1

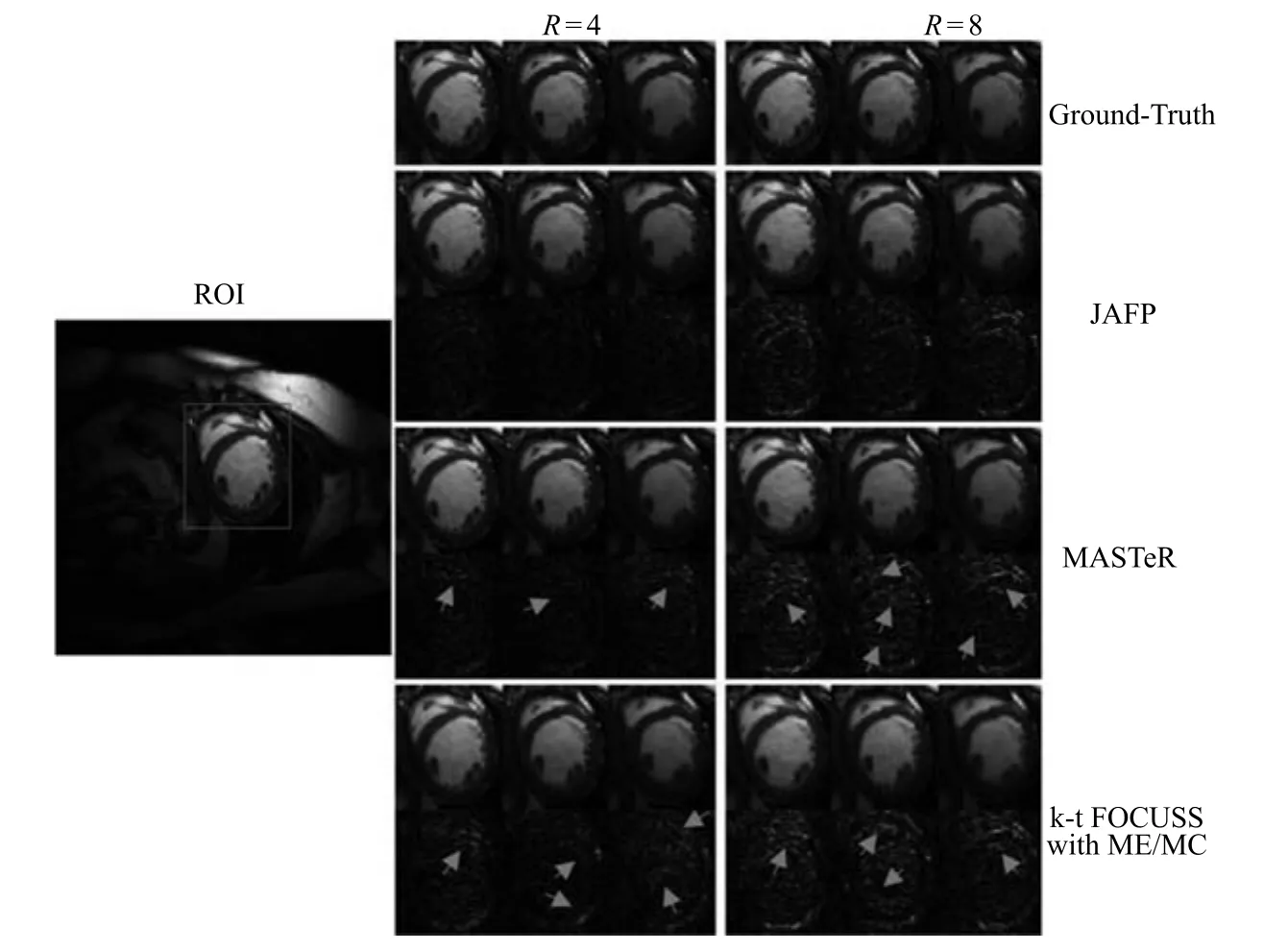
圖8　數據集1在4倍和8倍下采樣時,重建的ROI及其誤差圖Fig.8　The reconstructed ROI and errors with acceleration factors of 4 and 8 for dataset 1

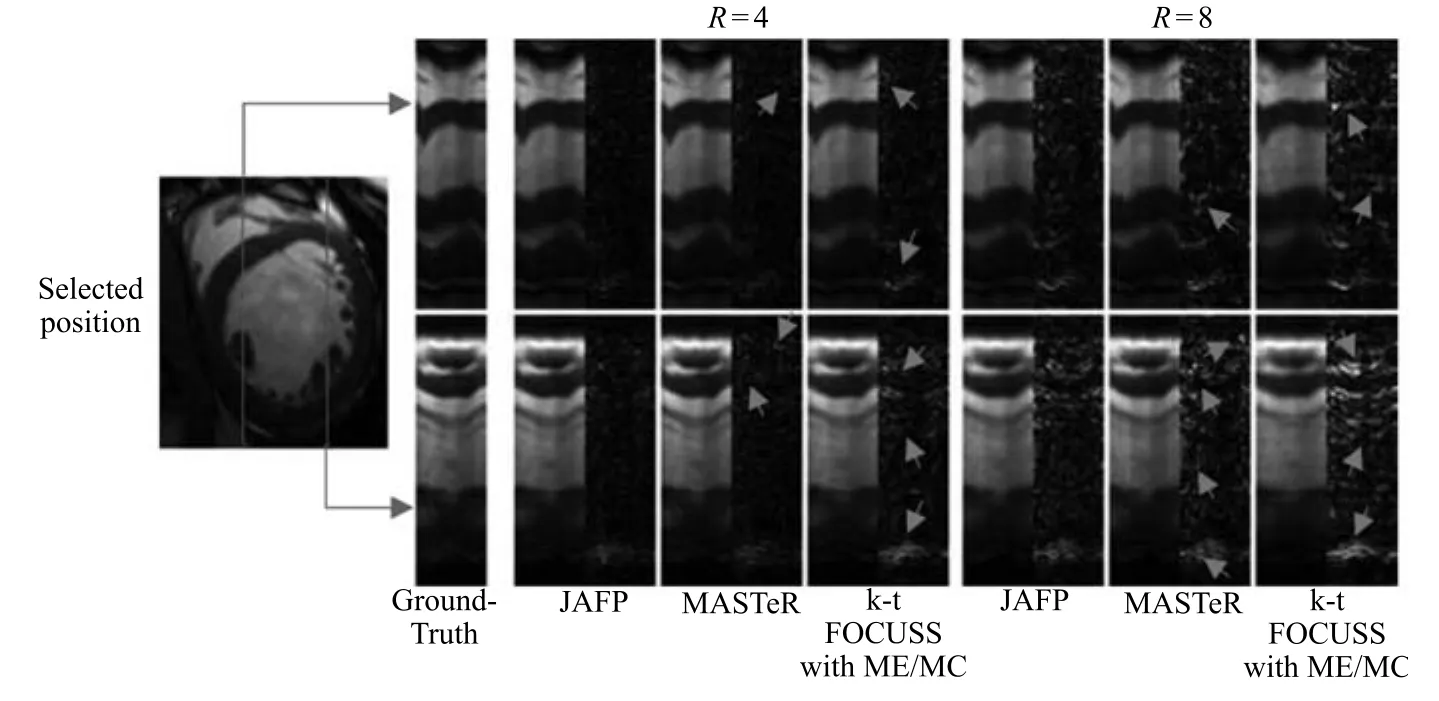
圖9　在4倍和8倍下采樣時,重建的時間域截面及其誤差圖Fig.9　The reconstructed temporal slices and errors with acceleration factors of 4 and 8

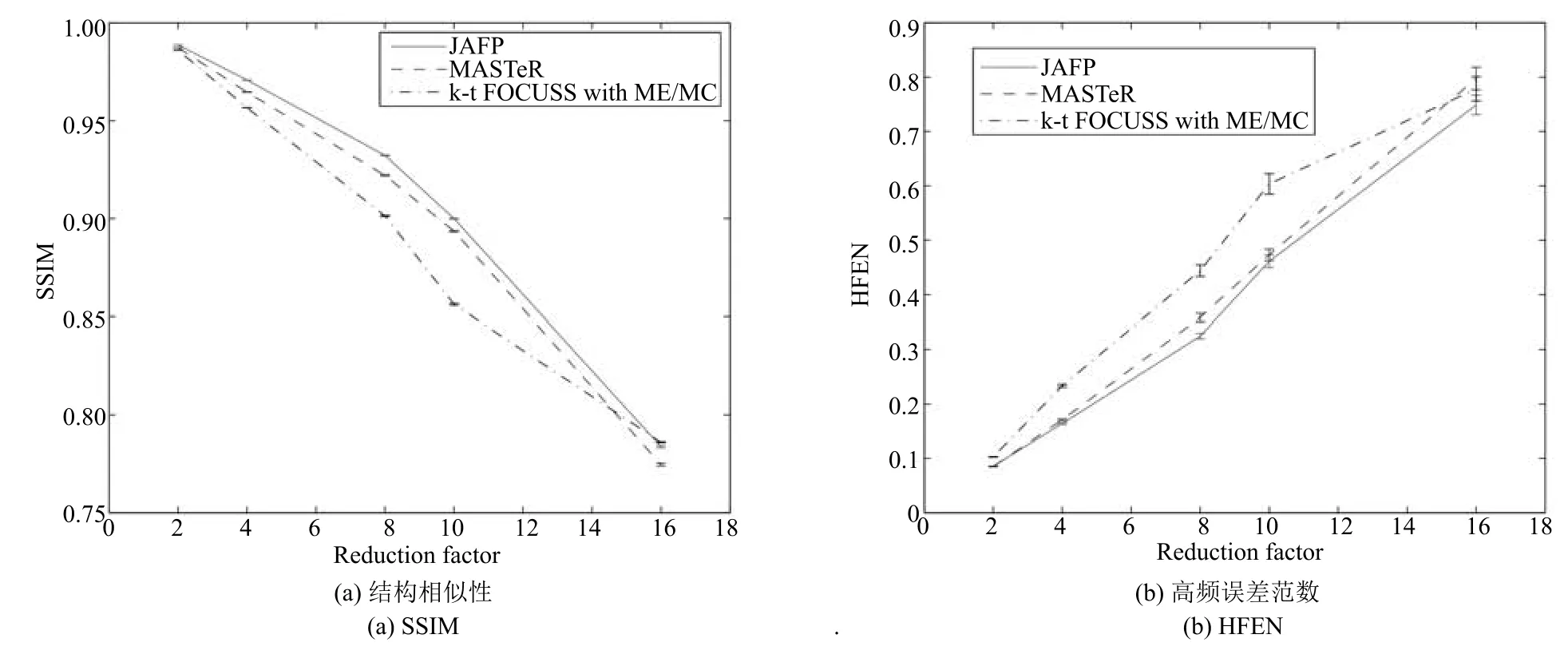
圖10　數據集1在不同下采樣倍數(2,4,8,10,16)下,不同方法重建綜合質量對比圖Fig.10　The comparison of reconstructed quality with acceleration factors of 2,4,8,10 and 16 for dataset 1

4.2　數據集2的實驗結果及分析

圖11(a)和圖12(a)展示了數據集2分別在4倍下采樣和8倍下采樣時,三種重建方法重建后每一幀圖像ROI區域的SSIM 對比圖.圖11(b)和圖12(b)展示了ROI區域的HFEN對比圖.顯然,具有更準確預測的JAFP方法重建結果在SSIM和HFEN兩項評價指標上均為最優.圖13和圖14分別比較了在8倍下采樣時各方法重建結果在兩個心臟壁區域(方框標注區域)收縮過程的灰度均值變化情況,由于JAFP方法較準確地預測了心臟的運動過程,使其在收縮過程重建結果與真實結果灰度均值的誤差絕對值明顯小于MASTeR和k-t FOCUSS ME/MC.

在重建誤差上,圖15分別呈現了數據集2在4倍下采樣和8倍下采樣時三種重建方法重建的ROI及其誤差圖.圖16呈現了數據集2在4倍下采樣和8倍下采樣時三種重建方法重建的時間域截面及其誤差圖.圖15共選取三幀圖像,分別為心臟收縮階段的第4幀、心臟收縮完全的第9幀以及舒張階段的第16幀.圖16選取了重建截面為原成像序列的第130列和第160列.盡管與數據集1完全不同,但從圖像上看,選取的這兩個位置仍然較為靠近心臟外壁,變化幅度較大,便于對比分析.由于預測效果的提升以及時間域稀疏約束的增加,無論是在重建的ROI誤差上,還是在重建截面上,JAFP的重建誤差明顯少于MASTeR和k-t FOCUSS ME/MC.

5　討論

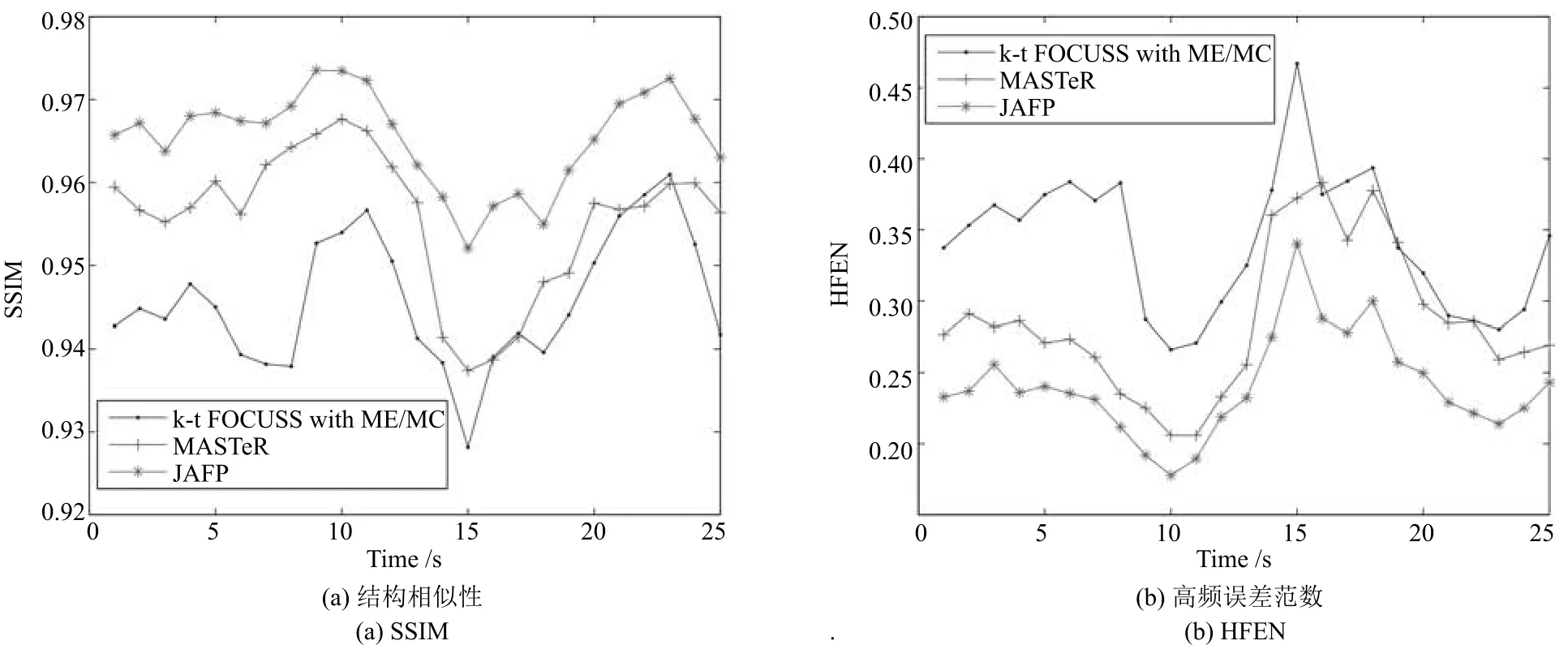
圖11　數據集2在4倍下采樣時重建質量比較Fig.11　The comparison of reconstruction quality with acceleration factor of 4 for dataset 2

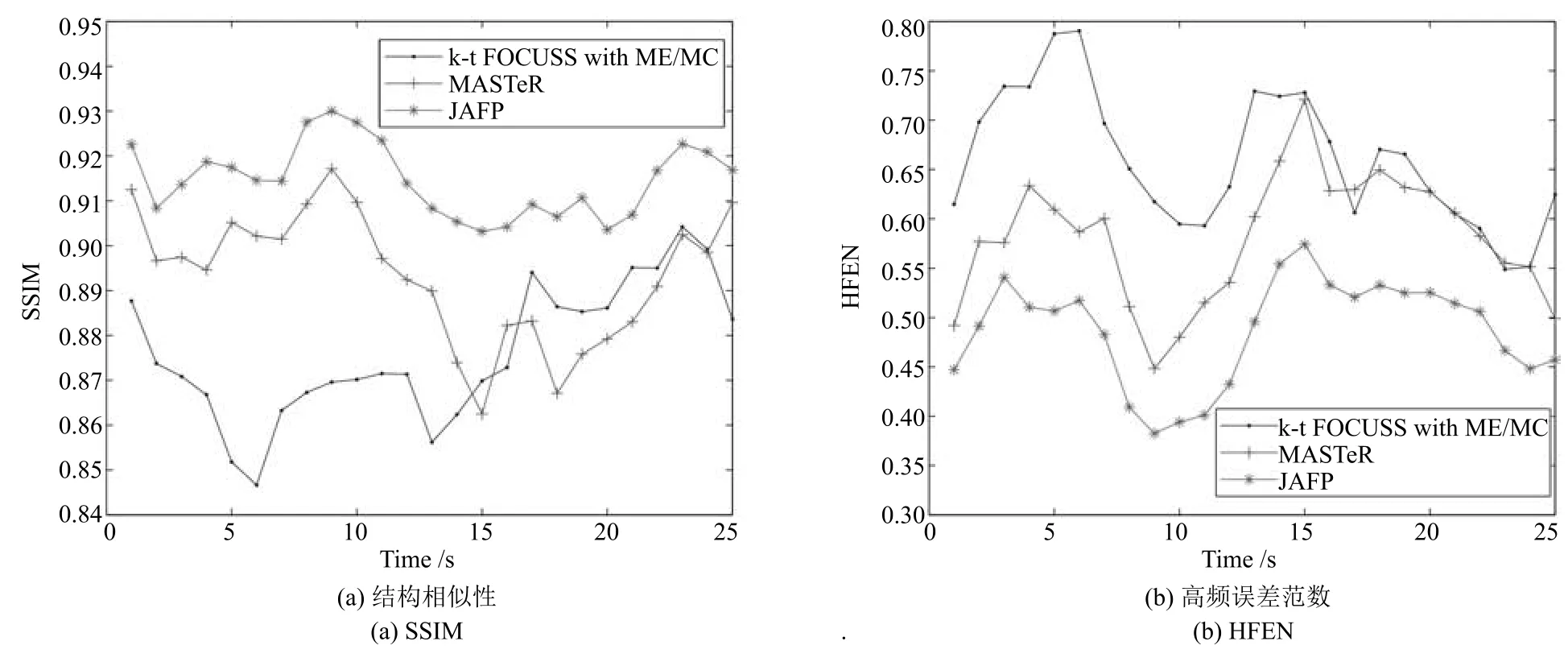
圖12　數據集2在8倍下采樣時重建質量比較Fig.12　The comparison of reconstruction quality with acceleration factor of 8 for dataset 2

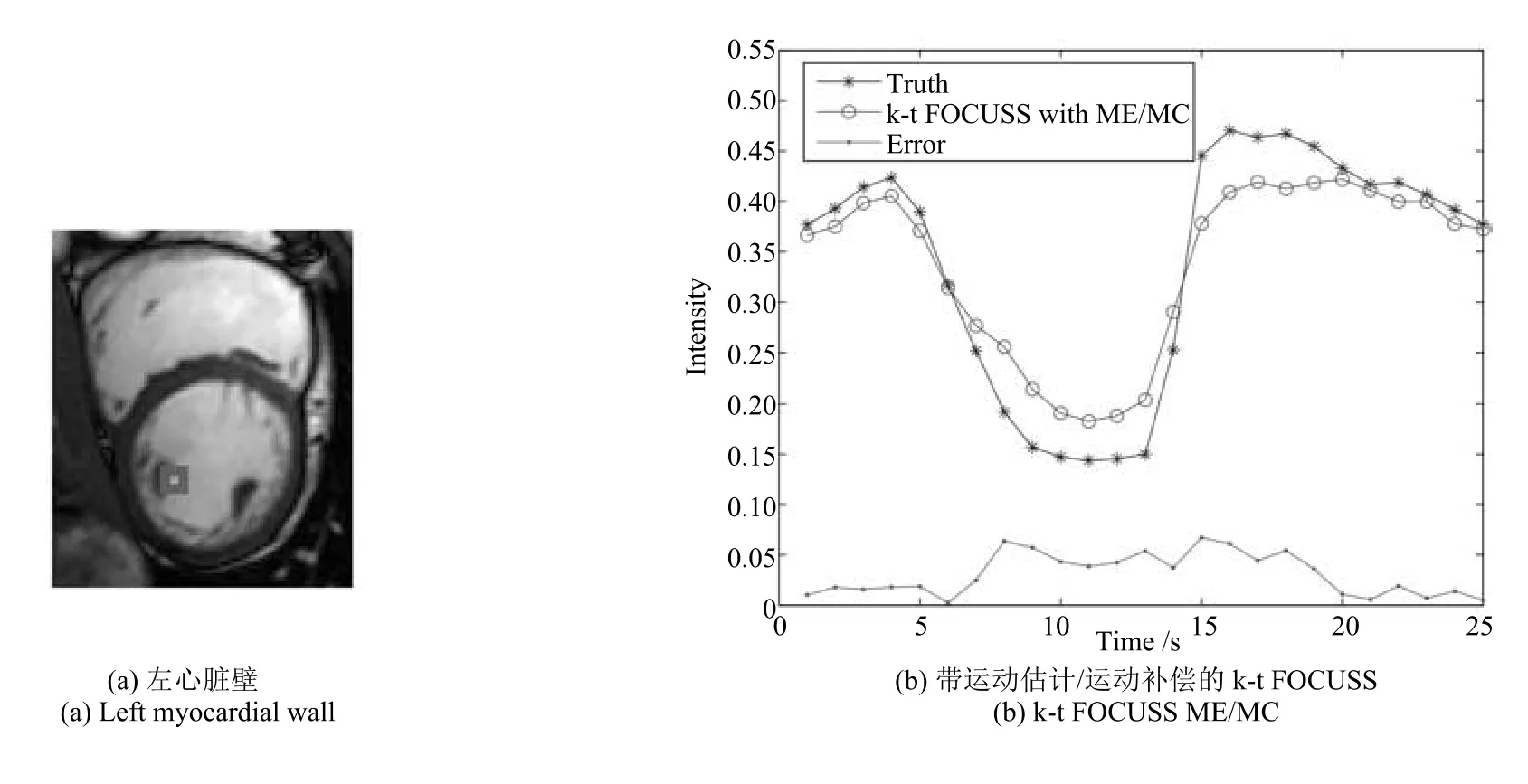
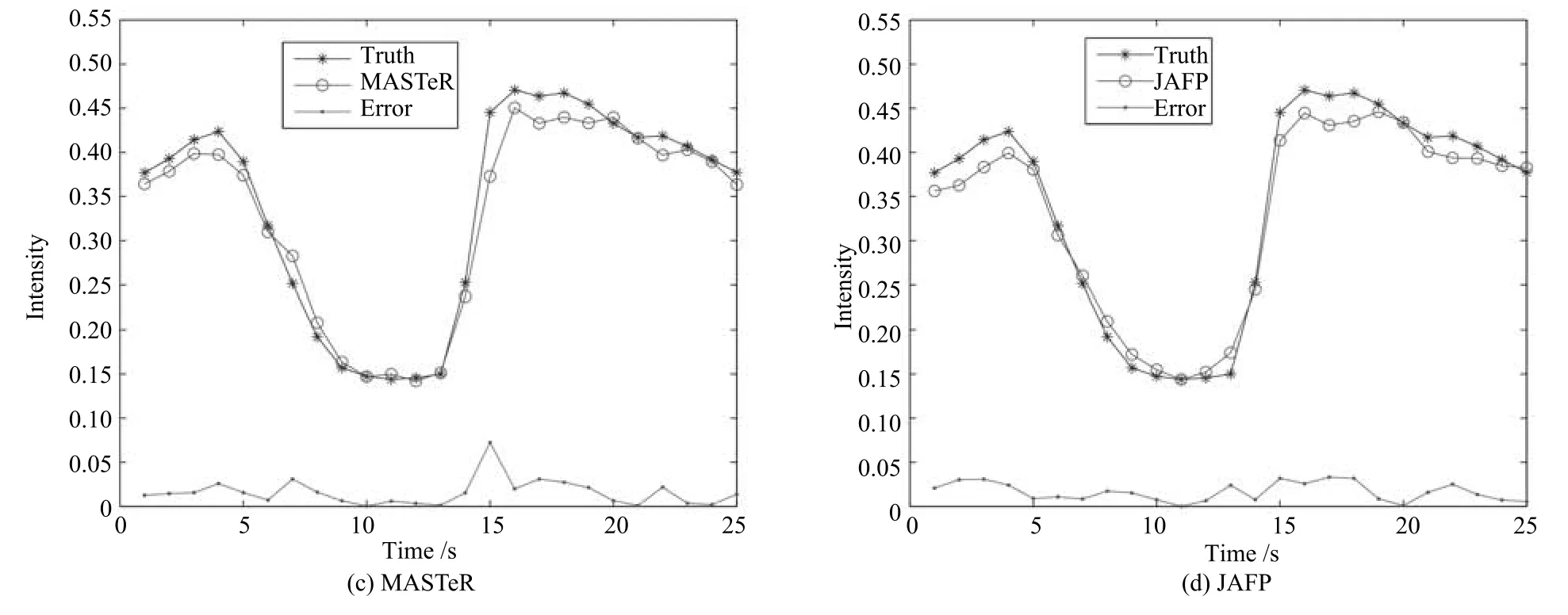
圖13　數據集2在8倍下采樣時左心臟壁灰度均值的比較Fig.13　The comparison of reconstructed gray average values and errors with acceleration factor of 8 for left myocardial wall of dataset 2

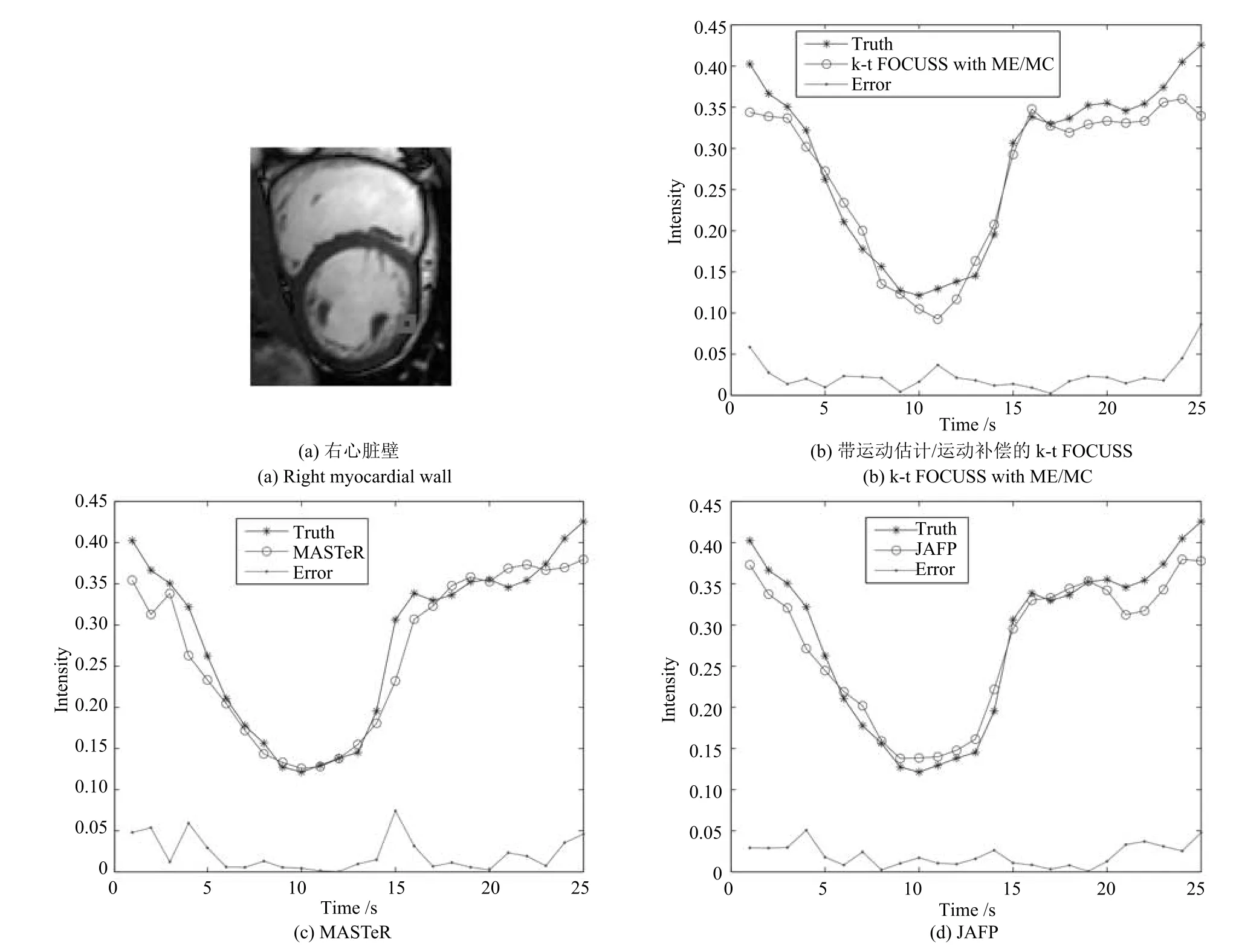
圖14　數據集2在8倍下采樣時右心臟壁灰度均值的比較Fig.14　The comparison of reconstructed gray average values and errors with acceleration factor of 8 for right myocardial wall of dataset 2

本文提出的JAFP方法與k-t FOCUSS ME/MC、MASTeR在模型上都利用了圖像差作為成像序列在空間域上的稀疏約束,但k-t FOCUSS ME/MC運動預測效果較差,而MASTeR又忽略了圖像差序列在時間上的冗余,限制了重建質量的進一步提升.JAFP在彌補二者不足的同時,還聯合相鄰幀預測進一步提升了預測的準確性.此外,由于JAFP方法在求解時僅需計算帶有一個約束的成像模型,使得其在計算效率上優于MASTeR.

圖15　數據集2在4倍和8倍下采樣時,重建的ROI及其誤差圖Fig.15　The reconstructed ROI and errors with acceleration factors of 4 and 8 for dataset 2

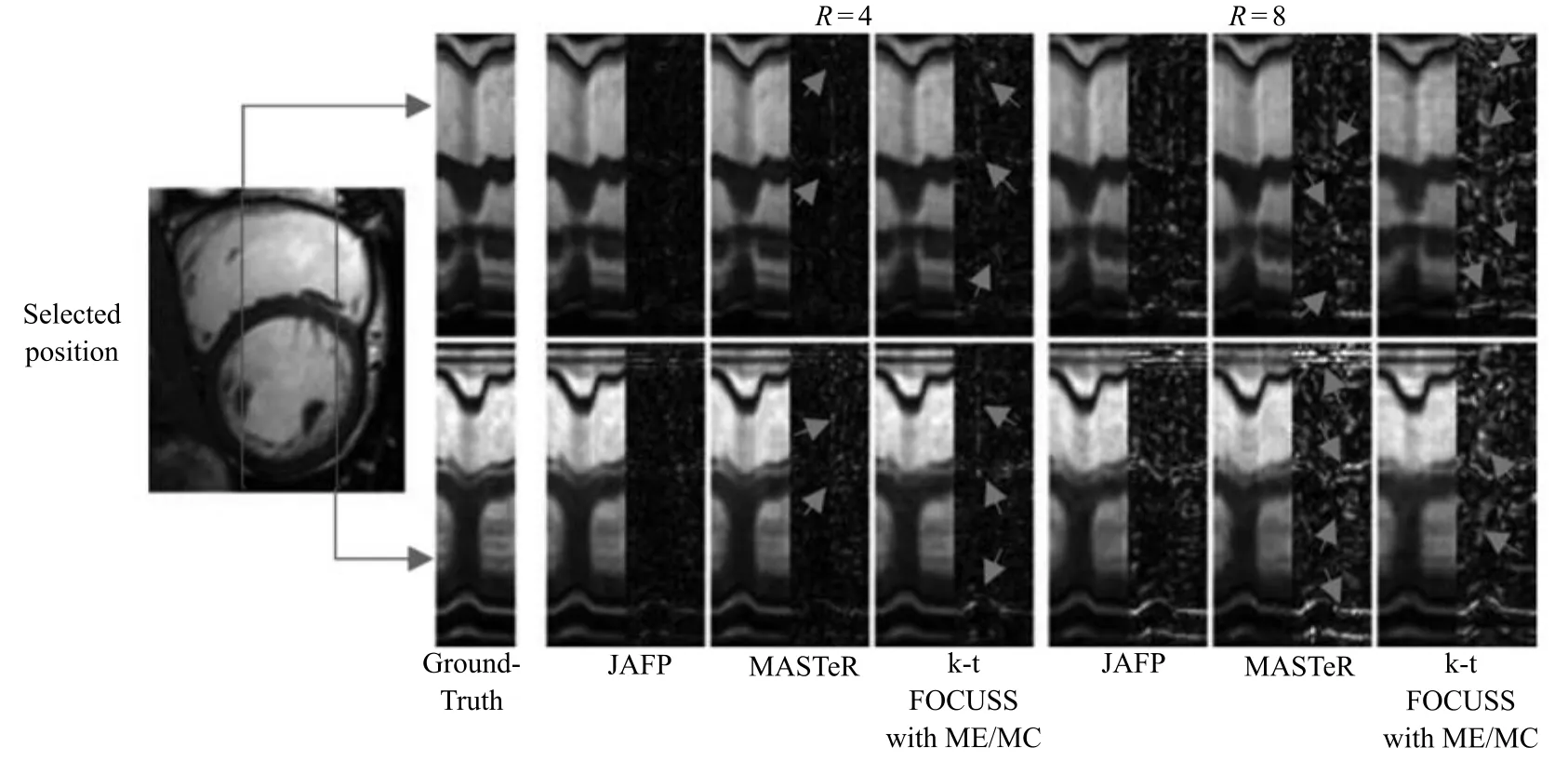
圖16　數據集2在4倍和8倍下采樣時,重建的時間域截面及其誤差圖Fig.16　The reconstructed temporal slices and errors with acceleration factors of 4 and 8 for dataset 2

5.1　聯合相鄰幀預測與其他預測方式的比較

JAFP在成像模型上與k-tFOCUSS ME/MC、MASTeR都用到了預測圖像,但JAFP的預測效果明顯優于二者.JAFP利用相鄰前后幀計算運動估計,在不需要引入額外的參考圖像的情況下,彌補了k-t FOCUSS ME/MC預測圖像質量較差的缺點.同時,JAFP聯合了相鄰前后幀的運動估計,其預測效果也優于MASTeR的單幀運動估計.

圖17展示了k-t FOCUSS ME/MC利用參考幀的運動估計的預測效果(ME based on ref Img),同時也展示了MASTeR利用相鄰的前一幀的運動估計的預測效果(F-Img)或利用相鄰的后一幀的運動估計的預測效果(B-Img),以及聯合相鄰幀運動估計的預測效果(0.5F+0.5B).從圖中可以看出,聯合相鄰幀運動估計的預測效果為最優.

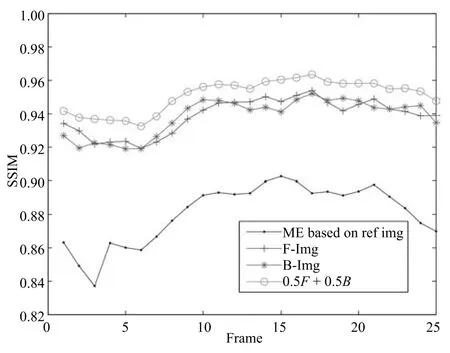
圖17　運動估計效果Fig.17　The quality of motion estimation

5.2　不同運動估計方案比較

5.3　算法收斂性分析

為了進一步說明該算法的收斂性,對數據集2計算過程的收斂速率進行了初步定量分析.實驗分別截取了該算法前7次迭代的重建圖像,如圖19所示.如圖19選取了心臟收縮階段的第5幀,并分別計算了前7次迭代重建的第5幀圖像ROI與原圖像的誤差圖,從圖中可以看出,其在第5次迭代時圖像誤差趨于穩定.

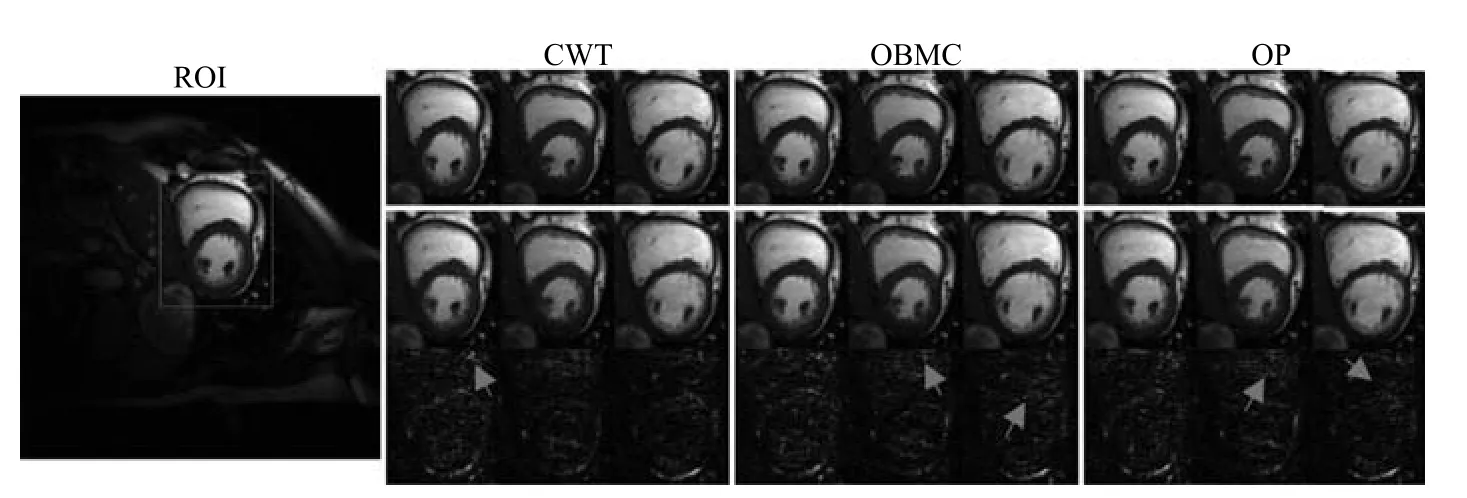
圖18　在8倍下采樣時,不同運動估計方法重建的ROI及其誤差圖(從左至右依次為心臟電影成像序列的第7幀、第12幀和第24幀ROI圖像)Fig.18　The reconstructed ROI and errors with different motion estimation plan(the reconstructed ROI of the 7th,12th,24th frames with acceleration factor of 8)

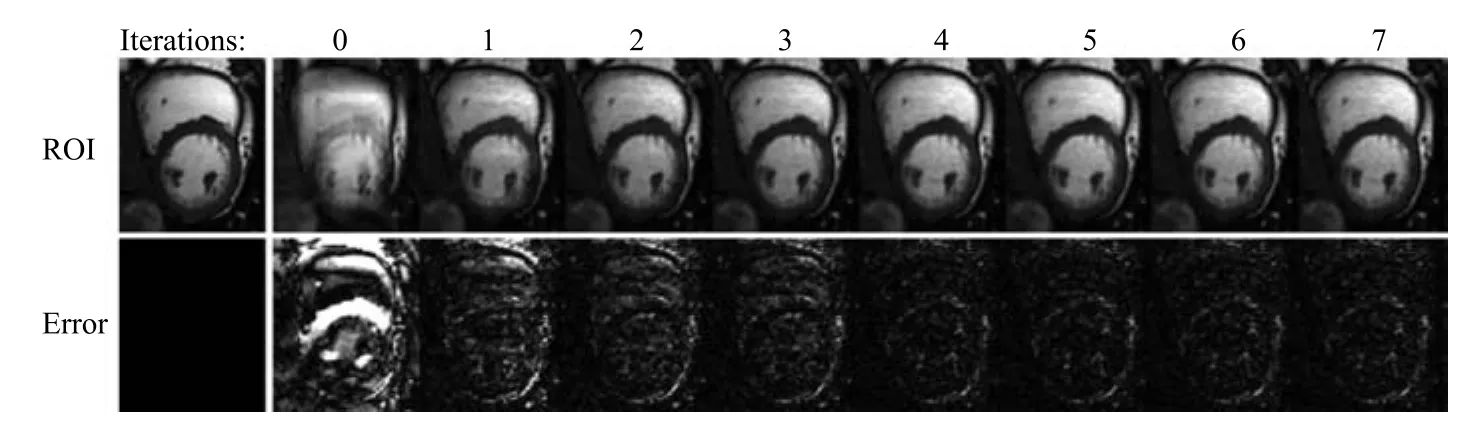
圖19　在8倍下采樣時,各迭代次數(0～7)下重建的第5幀圖像ROI及其誤差圖Fig.19　The reconstructed the 5th frame ROIs and errors by 0～7 times iteration

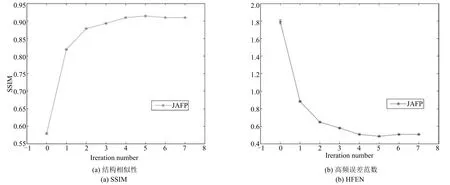
圖20　在不同迭代次數(0～7)下,JAFP方法重建綜合質量對比圖Fig.20　The comparison of reconstructed quality with 0～7 iterations

表1　運行時間對比Table 1　The comparison of runtime

同時,實驗對重建時前7次迭代下共25幀圖像序列的SSIM和HFEN兩項評價指標的均值和方差進行了對比,如圖20所示,JAFP重建方法在第5次迭代時,其重建結果的SSIM以及HFEN兩項評價指標均收斂.不難看出,JAFP初次迭代收斂迅速,且迭代的初始圖像越精確,收斂越快.對于閾值ε,實驗中的兩個數據集都設置ε=0.01,即前后兩次迭代的相對誤差小于1%時停止迭代.由于JAFP每一次迭代都將在前次迭代結果的基礎上前后向各做一次運動估計,根據式(11)可知,當迭代次數大于心臟運動周期時,運動估計的結果將與前一周期相近,不會持續提升重建質量.因此,JAFP算法的迭代次數受限于心臟運動周期,對于閾值的選取并不敏感.

5.4　算法效率比較

k-t FOCUSS ME/MC、MASTeR和JAFP三種算法均通過MATLAB實現仿真.為了比較其計算效率,三種算法均在相同的實驗環境下運行(雙核3.20GHz,4GB RAM,Windows 10),其計算時間及其迭代次數如表1所示.

由于MASTeR在求解時需計算兩個約束模型(前向圖像差稀疏約束和后向圖像差稀疏約束),而JAFP聯合前后幀預測中間幀圖像,僅需計算一個約束模型,因此其計算效率較MASTeR高.

6　結束語

本文利用相鄰幀之間的相似性,聯合相鄰前后兩幀為動態磁共振成像方法提出一種新的重建方法聯合相鄰幀預測(JAFP).JAFP分別計算前后兩幀與中間幀之間的運動估計,并聯合預測中間幀圖像.同時,利用心臟電影成像圖像序列與預測圖像序列的圖像差在時間域仍然具備擬周期的特性,增加時間域的稀疏約束,建立成像模型,在壓縮感知框架下完成重建.實驗結果表明,JAFP方法重建的圖像質量在SSIM和HFEN兩項評價指標上均獲得提升.雖然在實驗中只采用了動態磁共振成像的數據,但任意的動態成像問題均能根據相鄰幀之間的相似性,應用JAFP算法進一步提高成像質量,從而擴展了JAFP算法的應用范圍.盡管如此,由于JAFP方法在重建時,需要計算圖像序列在時間域的稀疏變換,因此JAFP方法難以擴展成為一種在線的重建方法.此外,在重建時更高質量的運動估計以及多樣的聯合預測方式,仍是JAFP重建方法在未來探究的重點.

1 Donoho D L.Compressed sensing.IEEE Transactions on Information Theory,2006,52(4):1289?1306

2 Li Shu-Tao,Wei Dan.A survey on compressive sensing.Acta Automatica Sinica,2009,35(11):1369?1377(李樹濤,魏丹.壓縮傳感綜述.自動化學報,2009,35(11):1369?1377)

3 Jing Nan,Bi Wei-Hong,Hu Zheng-Ping,Wang Lin.A survey on dynamic compressed sensing.Acta Automatica Sinica,2015,41(1):22?37(荊楠,畢衛紅,胡正平,王林.動態壓縮感知綜述.自動化學報,2015,41(1):22?37)

4 Peng Yi-Gang,Suo Jin-Li,Dai Qiong-Hai,Xu Wen-Li.From compressed sensing to low-rank matrix recovery:theory and applications.Acta Automatica Sinica,2013,39(7):981?994(彭義剛,索津莉,戴瓊海,徐文立.從壓縮傳感到低秩矩陣恢復:理論與應用.自動化學報,2013,39(7):981?994)

5 Qi Cong-Hui,Zhao Zhi-Qin,Xu Jing,Zhang Hai.Electromagnetic scattering and image processing of targets under complex environment based on compressive sensing method.High Power Laser and Particle Beams,2014,26(7):Article No.073206(齊聰慧,趙志欽,徐晶,張海.復雜場景下基于壓縮感知的目標電磁散射與成像.強激光與粒子束,2014,26(7):Article No.073206)

6 Qin Han-Lin,Han Jiao-Jiao,Yan Xiang,Zhou Hui-Xin,Li Jia,Zeng Qing-Jie.Infrared image reconstruction based on a modi fi ed block compressed sensing.High Power Laser and Particle Beams,2014,26(12):Article No.121011(秦翰林,韓姣姣,延翔,周慧鑫,李佳,曾慶杰.基于改進的分塊壓縮感知紅外圖像重建.強激光與粒子束,2014,26(12):Article No.121011)

7 Otazo R,Cand′es E,Sodickson D K.Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components.Magnetic Resonance in Medicine,2015,73(3):1125?1136

8 Ren Yue-Mei,Zhang Yan-Ning,Li Ying.Advances and perspective on compressed sensing and application on image processing.Acta Automatica Sinica,2014,40(8):1563?1575(任越美,張艷寧,李映.壓縮感知及其圖像處理應用研究進展與展望.自動化學報,2014,40(8):1563?1575)

9 Lai Z Y,Qux B,Liu Y S,Guo D,Ye J,Zhan Z F,Chen Z.Image reconstruction of compressed sensing MRI using graph-based redundant wavelet transform.Medical Image Analysis,2016,27:93?104

10 Song Lx,Zhang J G,Wang Q.MRI reconstruction based on three regularizations:total variation and two wavelets.Biomedical Signal Processing and Control,2016,30:64?69

11 Ye J,Qux B,Guoh,Liu Y S,Guo D,Chen Z.Patch-based directional redundant wavelets in compressed sensing parallel magnetic resonance imaging with radial sampling trajectory.Journal of Medical Imaging and Health Informatics,2016,6(2):387?398

12 Ak?cakaya M,Bashat A,P fl ugi S,Foppa M,Kissinger K V,Hauser Th,Nezafat R.Localized spatio-temporal constraints for accelerated CMR perfusion.Magnetic Resonance in Medicine,2014,72(3):629?639

13 Li Q Y,Qux B,Liu Y S,Guo D,Lai Z Y,Ye J,Chen Z.Accelerating patch-based directional wavelets with multicore parallel computing in compressed sensing MRI.Magnetic Resonance Imaging,2015,33(5):649?658

14 Majumdar A,Ward R.Learning space-time dictionaries for blind compressed sensing dynamic MRI reconstruction.In:Proceedings of the 2015 IEEE International Conference on Image Processing.Quebec,Canada:IEEE,2015.4550?4554

15 Li J S,Sun J Q,Song Y,Zhao J.Accelerating MRI reconstruction via three-dimensional dual-dictionary learning using CUDA.The Journal of Supercomputing,2015,71(7):2381?2396

16 Tsao J,Kozerke S.MRI temporal acceleration techniques.Journal of Magnetic Resonance Imaging,2012,36(3):543?560

17 Kim D,Dyvorneh A,Otazo R,Feng L,Sodickson D K,Lee V S.Accelerated phase-contrast cine MRI using k-t SPARSE-SENSE.Magnetic Resonance in Medicine,2012,67(4):1054?1064

18 Jungh,Ye J C,Kim E Y.Improved k-t BLAST and k-t SENSE using FOCUSS.Physics in Medicine and Biology,2007,52(11):3201?3226

19 Jungh,Sung K,Nayak K S,Kim E Y,Ye J C.k-t FOCUSS:a general compressed sensing framework for high resolution dynamic MRI.Magnetic Resonance in Medicine,2009,61(1):103?116

20 Asif M S,Hamilton L,Brummer M,Romberg J.Motionadaptive spatio-temporal regularization for accelerated dynamic MRI.Magnetic Resonance in Medicine,2013,70(3):800?812

21 Dongx L,Liuh W,Xu Y L,Yangx M.Some nonlinear conjugate gradient methods with sufficient descent condition and global convergence.Optimization Letters,2015,9(7):1421?1432

22 Gorodnitsky I F,Rao B D.Sparse signal reconstruction from limited data using FOCUSS:a re-weighted minimum norm algorithm.IEEE Transactions on Signal Processing,1997,45(3):600?616

23 Ruan Qin-Jie.The Study of Fast Dynamic Magnetic Resonance Imaging Based on Compressed Sensing Technique[Master thesis],Hangzhou Dianzi University,China,2014.(阮欽杰.基于壓縮感知技術的快速動態磁共振成像技術研究[碩士學位論文],杭州電子科技大學,中國,2014.)

24 Orchard Mt,Sullivan G J.Overlapped block motion compensation:an estimation-theoretic approach.IEEE Transactions on Image Processing,1994,3(5):693?699

25 Ji Li-Xia,Li Xue-Xiang.Algorithm and simulation of image stabilization for high speed moving target images based on adjacent frames compensation.Computer Science,2014,41(7):310?312,317(姬莉霞,李學相.基于相鄰幀補償的高速運動目標圖像穩像算法及仿真.計算機科學,2014,41(7):310?312,317

26 Zhaot S,Wang Jh,Wang Z,Chen C W.SSIM-based coarse-grain scalable video coding.IEEE Transactions on Broadcasting,2015,61(2):210?221

27 Maligranda L.Some remarks on the triangle inequality for norms.Banach Journal of Mathematical Analysis,2008,2(2):31?41

28 Fang Sheng.Regularization-based Parallel Magnetic Resonance Imaging Technique for Highly Accelerated Data Acquisition[Ph.D.dissertation],Tsinghua University,China,2010.(方晟.基于正則化的高倍加速并行磁共振成像技術[博士學位論文],清華大學,中國,2010.)

29 Sun S J,Gill M,Li Y F,Huang M,Byrd R A.Efficient and generalized processing of multidimensional NUS NMR data:the NESTA algorithm and comparison of regularization terms.Journal of Biomolecular NMR,2015,62(1):105?117

30 MagareyJ,KingsburyN.Motionestimationusinga complex-valued wavelet transform.IEEE Transactions on Signal Processing,1998,46(4):1069?1084

31 Broxt,Bruhn A,Papenberg N,Weickert J.High accuracy optical fl ow estimation based on a theory for warping.In:Proceedings of the 8th European Conference on Computer Vision.Berlin Heidelberg,Germany:Springer,2004.25?36

32 Wang Bing,Zhao Rong-Chun,Jiang Xiao-Yue,Yu Hong-Bo.Motion estimation based on wavelet transform.Journal of Northwestern Polytechnical University,2004,22(4):417?421(王兵,趙榮椿,蔣曉悅,俞鴻波.一種基于小波變換的運動估計方法.西北工業大學學報,2004,22(4):417?421)

33 Li Zhi-Qing,Shi Zhi-Ping,Li Zhi-Xin,Shi Zhong-Zhi.Sparse coding model based on structural similarity.Journal of Software,2010,21(10):2410?2419(李志清,施智平,李志欣,史忠植.基于結構相似度的稀疏編碼模型.軟件學報,2010,21(10):2410?2419)

34 Ravishankar S,Bresler Y.MR image reconstruction from highly undersampled k-space data by dictionary learning.IEEE Transactions on Medical Imaging,2011,30(5):1028?1041