借助意義教學促進有效建模

朱子健

[摘 要]模型思想是數學課程標準修訂過程中新增加的一個核心詞。以“乘法分配律”一課為例，談談如何借助意義教學來實現有效建模，讓學生經歷將實際問題抽象成數學模型并進行解釋與應用的過程，進而使學生獲得對數學理解的同時，在思維能力、情感態度與價值觀等多方面得到進步和發展。

[關鍵詞]數學建模；意義教學；乘法分配律

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2018）08-0020-02

人教版教材第八冊中的“乘法分配律”教學內容一直以來都是小學數學教學中的一個難點，學生學習的成效會直接影響后續的學習。常見的教學流程為“給出一個問題背景→強調從計算人手→急于比較、研究→引導觀察→過早地給出結論→得出乘法分配律→機械式地套用→利用練習鞏固知識”。在這個教學過程中，學生通過記憶和重復練習來建立數學模型，但不知道為什么乘法分配律會成立，對乘法分配律的意義理解不透。這并不利于學生掌握知識的本質，還會導致學生運用乘法分配律時經常出現這樣的錯誤：第一個加數乘上乘數后，就直接加上另一個加數，另一個加數沒有乘上乘數，就完成計算了。如 （8+7）×125=8×125+7，錯誤的根本原因是對“乘法分配律”的意義理解不夠深刻。

《義務教育數學課程標準（2011版）》明確指出：“讓學生經歷將實際問題抽象成數學模型并進行解釋與應用的過程，進而使學生獲得對數學理解的同時，在思維能力、情感態度與價值觀等多方面得到進步和發展。”因此，我提出意義建模法：強調從乘法的意義人手，引導學生深刻理解為什么乘法分配律會成立，從而幫助學生掌握知識，從而建立數學模型。而數學建模通常以“問題情境——建立模型——解釋應用與拓展”的基本形式展開。

一、運用幾何直觀，數形結合充分感知模型

課程標準強調數學教學要“從學生已有的生活經驗出發，讓學生親身經歷將實際問題抽象成數學模型并進行解釋與應用的過程”。因此，教師首先要引導學生從生活原型中提煉出數學模型，并在初步感知模型的基礎上，逐步建構模型。

【教學片段1】

師：春裝校服75元一套。小劉家買了2 套，小李家買了3套。他們兩家一共要付多少元？

生1：75×2+75×3=150+225=375（元）。

師：75×2與75×3分別算出的是什么？為什么用乘法計算？（學生回答略）

師：如果說75×（2+3）=75×5=375（元），（2+3）算出的5是什么？75×5表示什么？

生2：表示5個75相加的和是多少。

師：通過計算你們發現了什么？

生3：75×（2+3）=75×2+75×3。

師：如果不計算，你能說明75×（2+3）與75×2+75×3相等嗎？

生4：等式左邊表示5個75相加，等式右邊表示2個75加上3個75，都是5個75相加。

學生已經學習了乘法的基礎知識，知道用乘法可以求幾個相同加數的和。基于本節課數學建模的需要，復習乘法的意義也就成為學習乘法分配律的立足點與起點。在新舊知識的連接點上開拓學生的思維，使新知的教學起點與學生已有的舊知緊密相連，就能使新知成為舊知的自然延伸、發展，做到環環緊扣、步步遞進，把知識串成一條知識線，幫助學生掌握知識整體。

【教學片段2】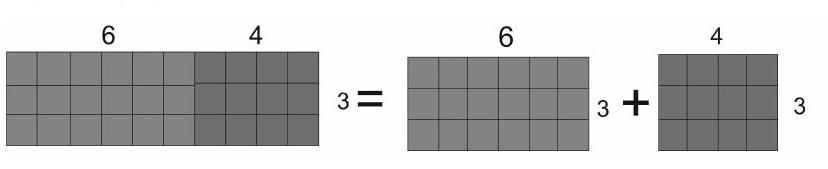

師：結合下圖，與同桌說說等式（6+4）×3=6×3+4×3為什么會成立。

生：圖的左邊可以理解為10個3相加，圖的右邊分別是6個3相加和4個3相加，也就是10個3相加，所以（6+4）×3=6×3+4×3。

為了順應中年級學生的思維特點，小學數學的建模教學應當充分運用這種幾何直觀教學法。學生已經熟練掌握長方形的面積計算方法，只要圖式結合，算理就一目了然。在學生思考的過程中，教師要注意并重視培養學生在表達和交流過程中語言描述的能力，為學生總結乘法分配律做好鋪墊。數學是研究現實世界數量關系和空間形式的科學，形與數往往是聯系在一起的，因此，數與形之間存在著本質的聯系。在教學過程中，教師要強調乘法的意義，并以這種數形結合的方式生動形象地幫助學生解釋“乘法分配律”的本質意義，這樣不僅能為后面的模型應用做足準備，也有助于學生形成數學建模思想。

二、意義教學，抽象并建構模型

初步感知模型后，教師要提供更多類似的、系列的學習材料來為學生進一步感悟模型做鋪墊，并給予學生足夠的思考時間，讓學生在舉例子的過程中一步一步地將發現的規律準確地加以描述和歸納，最終建立數學模型。

【教學片段3】

1.觀察等式，探索規律

師（在學生完成題目后）：觀察這幾組等式，你有什么發現？

師（引導學生觀察左右兩邊算式的特點）：左邊的算式都是兩個數的和與一個數相乘；右邊的算式都是這兩個數與這個數分別相乘，再相加；左右兩邊的計算結果相等。

2.舉例驗證，歸納規律

師：這個計算規律是否在哪里都成立呢？我們能不能再舉些類似的例子來驗證一下？請同桌之間互相說一說。

生1：我舉的例子是（4+5）×15=4×15+5×15。

師：這個式子的左右兩邊分別表示什么？

生1：左邊表示9個15的和；右邊表示4個15的和，加上5個15的和。

生2：我舉的例子是（5+3）×6=5×6+3×6。

師：請你解釋一下。

生2：左邊表示8個6的和，右邊是5個6與3個6的和。8個6的和等于5個6與3個6的和。

生3：（20+10）×3=20×3+10×3。

師：請你解釋一下。

生3：左邊是30個3相加；右邊是20個3相加，再加上10個3相加，加起來就是30個3相加。

師：同學們舉了不同的例子來驗證我們的發現，看來這個計算規律是成立的。這個計算規律在數學中就叫作“乘法分配律”。如果別人問你，什么叫“乘法分配律”，你該怎樣告訴他呢？能用自己的語言描述這個規律嗎？

生5：兩個數的和與一個數相乘，等于這兩個數分別與那個數相乘，再相加。

師：把“那個數”改為——“這個數”。

（教師讓學生獨立思考：（▲+█）×●=？師生共同抽象出數學模型：（▲+█）×●=▲×●+█×●；在肯定了學生或不太嚴謹，或不太全面的回答之后，師生共同歸納乘法分配律：兩個數的和與一個數相乘，可以先把它們與這個數分別相乘，再相加。最后，請學生把課本翻到26頁，讀一讀這個規律，并在讀的過程中體會規律。）

3.交流總結，表示規律

師：用數學的語言——數學符號來表示規律，得出“乘法分配律”的字母公式“ （a+b）×c=a×c+b×c”。

數學表象是對客觀事物從形式或結構等方面概括而得到的觀念性表象，圖式表象是其中的一種類型。乘法分配律的圖式表象是（▲+█）×●=▲×●+█×●的模式形象。學生在初步感知計算規律的狀態下，通過觀察、比較，發現規律，并嘗試用自己的語言描述規律，最后用數學的語言簡化規律，歸納出“乘法分配律”的字母公式。這種語言的描述就是嘗試著將數學的實際規律抽象化，就是建立數學模型的過程，這是數學建模最為艱難也是最為關鍵的一步。要較好地完成這一步，在數學建模過程中，教師應當不失時機地讓那些有能力的學生嘗試用符號語言建構和表達模型。

三、解決問題，解釋并應用模型

在乘法分配律這一數學模型的具體運用過程中，有相當多的學生在從a×c+b×c=（a + b）×c過渡到 （a + b）×c= a×c+b×c的過程中存在障礙，只能停留在a個c加b個c等于（a + b）個c的模型中，缺乏對乘法分配律這一數學模型逆向運用的一種直觀的感知和深度的理解。因此，如何幫助學生順利實現這一過渡，尤為重要。加強練習，強化乘法意義的理解，內化模型，是實現有效建模的途徑。

1.基本練習：根據乘法分配律，填上適當的數。

（12+40）×3= ×3+ ×3

15×（40+8） = 15 × +15×

35×69 + 35×31=（ + ）×35

2.辨析練習：判斷對錯。

56×（19+28） = 56×19 + 28（ ）

32×（7×3） = 32×7 + 32×3（ ）

64×64+ 36×64 =（64+ 36）×64 （ ）

3.完成課本第26頁第2題，用豎式計算25×12= ？觀察豎式，說說在計算過程中運用了什么運算定律。

（板書： 25×12=25×（2+10）=25×2+25×10=50+250=300）

數學學習可以分為機械學習與有意義學習，而有意義學習要靠理解。意義建模法強調從乘法的意義入手， 在“生活數學”與“學科數學”之間搭建橋梁，引導學生從生活原型中提煉出數學模型，以數形結合的方式生動形象地幫助學生準確把握運算律的本質及其教學價值，強化乘法分配律的本質意義。這樣，不僅有利于提高相關教學活動的針對性和有效性，而且有利于學生對“乘法分配律”這個知識點的意義的建構，感悟蘊含在運算律知識及相關學習活動過程中的基本數學思想。

[ 參 考 文 獻 ]

[1] 汪繩祖主編.小學數學教育學（1997 年11月第1版）[M].北京：高等教育出版社，1997.8.

[2] 曹培英.數學課程標準核心詞的實踐解讀之八-模型思想（上）[J].小學數學教師，2014（12）.

[ 3] 曹培英.數學課程標準核心詞的實踐解讀之八-模型思想（下）[J].小學數學教師，2015（2）.

（責編 金 鈴）