從“海綿式”思維到“淘金式”思維的提問對比

劉永萬

[摘 要]對教師“滿堂問”和學生“點問”的現狀做出剖析，通過分析和對比教師“海綿式”思維的提問和學生“淘金式”思維的提問，指出“海綿式”思維的弊端，說明“淘金式”思維的必要性，給“讓學生的學習真正發生”指明了方向。

[關鍵詞]提問；精確；思維

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2018）08-0030-02

本文所討論的“海綿式”思維和“淘金式”思維，指的是教師提問和學生提問過程中不同的思維方式，如下表所示：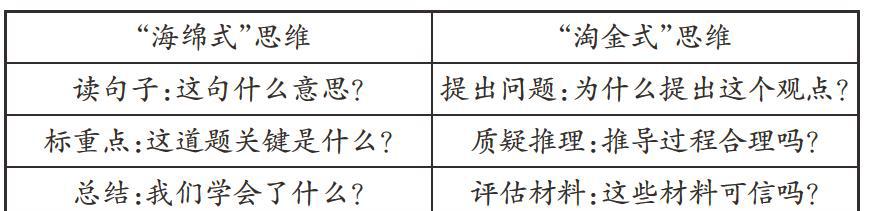

一、教師的提問

教師的提問對學生的學習來說屬于海綿式思維——吸收以及儲備知識，相對被動。分析如下。

1.教師提問“開放”——學生思考迷失方向

提問的“開放”是指提出的問題過于寬泛，沒有嚴格規定的答案，給學生以充分自由發揮的空間。但這樣的提問往往比較松散，缺乏方向。

【案例1】對于蘇教版教材二年級下冊“數據收集和整理”的情境圖（如下圖），不少教師會提問：你打算如何分類？

由于學生不知道分類的目的和需求是什么，很難說出分類標準，導致不知如何分類。

其實，教材上就給出了很好的提示——你想知道什么？對此，教師就可以提問：要想知道學生比老師多多少人，如何分類？要想知道參加哪項活動的人數最多，參加哪項活動的人數最少，如何分類？

2.教師提問“虛假”——非學生的訴求

個人主義或經驗不足的人提出的問題往往是虛假的，不是非真正的、主要的問題，反而會增加學生的負擔。因為教師杜撰出來的問題，根本不是學生的問題，學生不感興趣，覺得沒意思，只能配合教師表演。

3.教師提問“瑣碎”——打斷學生的思維

教師為了避免滿堂灌的嫌疑，往往會把需要解決的問題肢解得支離破碎后進行一問一答式的教學模式，使學生處于被動狀態，這樣課堂缺少生機和生命力。

【案例2】教學“加法交換律和結合律”時，課始，教師給出兩組口算，讓男學生口算第一組，女學生算第二組，看誰算得快。

第1組 8+177 65+ 12 27+ 36

第2組 177+8 12+65 36+27

做完這兩組題，這節課研究的重點是什么，這樣做的目的是什么，學生還是不知道，他們還以為是比計算速度。其實，每一列的上下兩個算式都是新知的整體呈現，教師應該讓學生把每一列的兩個算式一起完成。

4.教師提問封閉——學生思維定式

（1）縱向線性化，缺乏橫向偏平化

【案例3】教學“圓柱的認識”時，在學生學習了一個側面、2個底面、無數條高之后，教師總會追問：形和體的關系是什么？如一個長方形沿著一條邊旋轉一周，會形成什么圖形？無數個同樣大小的圓疊加，會得到什么圖形？從側面看圓柱體，看到的是什么圖形？從上面看圓柱體，看到的是什么圖形？

很少有教師會問“物體為什么會做成圓的？”即使問了，教師給出的答案無非是“節省材料、便于拿、不容易壞等，我們今后將要學習”，一言帶過。我是這樣問的：“為什么摩天大樓的上部通常是圓的？”學生的思考與回答令我十分興奮：“高空物體所受的作用力主要是風?！薄澳μ齑髽侨绻情L方體，風的垂直作用力可能在一個面上。”“摩天大樓是圓柱體，風的垂直作用力在一條棱上?！薄@不僅溝通了圓柱與長方體的面、棱的認識，還溝通了數學與科學間的聯系，使學生的認識更豐滿、更有價值。

（2）知識結構封閉化，缺乏開放創新

【案例3】教學“分數乘整數”時，教師往往是先復習幾個相同整數相加，再教學教材的例題，然后提出“分數乘整數的意義與整數乘法的意義相同，都是表示幾個相同加數的和的簡便計算”，最后通過讓學生做幾道題目，總結計算方法“分母不變，分子與整數相乘”。這樣的一節課，可能會造成若干年后，學生在算36×0.25時都是“（9×4）×0.25=9×（4×0.25）=9×1=9”，不會想到“36×1/4=9”。

這節課是分數乘法的一部分，教師要有分數的概念，還要清楚小數是分數的一種特殊形式。因此，課始引入時可以給出幾個相同小數相加的算式，加強小數和分數的聯系，打破學生的定式思維。

二、學生的提問

1.闡述性提問——指向題意的理解

【案例4】 題目：一批葡萄重1000千克，含水量為98%，蒸發掉一部分水后，葡萄含水量為97.5%，這時的葡萄有多少千克？

學生會問：“我的列式是1000×97.5%，為什么是錯的？”出現這種錯誤的原因是對題目不理解。此時，教師可以指導學生先把題目讀一遍，找出單位“1”，以及誰是誰的幾分之幾，學生就知道錯因了：98%是原來總重量的98%，97.5%是蒸發掉一部分水后，是剩下的總重量的97.5%。

學生還會問“2%呢？2%跑哪去了？”教師只要告訴學生 2%沒“跑”，是果肉的含量即可。

至此，學生就能厘清思路：設這時的葡萄有х千克，列式為1000×2%=х×2.5%。

2.假設性提問——指向知識點與實際表達的連接

“如果沒有……，將會怎么樣？” 這樣的假設性提問能夠豐富知識的內涵和外延，學生在提問的過程中能夠鞏固知識，能夠培養和發展自身的想象能力和思維能力。

【案例5】題目：一塊長方形地，長為24米，寬為18米，在它的四周等距離栽樹，四個角上都栽，至少栽多少棵？

“如果畫草圖，能夠發現什么？”——等距離求的就是24和18的公因數。

“如果四個角上都不栽樹？” ——至少栽2棵。

“如果每條邊的中點上也栽樹？”——等距離求的就是12和9的公因數。

學生在這樣提問中理解了公因數的實際表達，假設性提問就相當于把題目進行變式，擴展了知識的內涵和外延。

3.比較性提問——指向相近的思路

在通過比較性提問比較事物異同的過程中，學生的觀察、分析、推理能力都能得到培養。

【案例6】題目：為了鼓勵市民避開用電高峰期間用電，供電部門實行峰谷用電制度，每天8時至12時之間，用電每度電價0.55元（峰時電價），21時至次日8時之間，用電每度電價是0.35元（谷時電價）。

（1）小華家在某月使用峰谷電后，峰時用電量是谷時用電量的1/2，共付電費50元。該家庭當月使用峰時電量和谷時電量各多少度？

（2）小明家某月用電120度，按峰谷用電制度計價，共付電費46元。該家庭當月使用峰時電量和谷時電量各多少度？

解題思路為什么不同？——峰時用電量與谷時用電量數量關系不同。第（1）題中，峰時用電量=谷時用電量×1/2，用替換法，得到50÷（0.55×1/2+0.35）；第（2）題中，峰時用電量+谷時用電量=120，用假設法，得到（46-120×0.35）÷（0.55-0.35）

可以用同一種方法嗎？——可以都用假設法（方程）。第（1）題中，假設谷時用電量為х度，峰時用電量為1/2х，得到0.55×1/2х+0.35×х=50；第（2）題中，假設谷時用電量為х度，峰時用電量為（120-х）度，得到0.55×（120-х）+0.35×х=46。

綜上，對比教師的提問和學生的提問，可以看出“海綿式”思維和“淘金式”思維對教學的影響。顯然，只有“淘金式”的思維才能真正引領學生的學習真正發生，才能使學生成為學習的主體。

（責編 童 夏）