同步坐標系下異步感應電機外轉子彈性振動分析

王世宇， 夏 營， 孫文嘉， 王堯堯

(1. 天津大學 機械工程學院， 天津 300072； 2. 天津市非線性動力學與控制重點實驗室， 天津 300072；3. 上海航天控制技術研究所， 上海 201109)

外轉子異步電機以其結構緊湊和功率損耗小等優點廣泛應用于冷卻風機等領域。由于結構的特殊性，尤其是可產生顯著彈性變形的外轉子的應用，在旋轉磁載荷作用下，更容易產生彈性振動和噪聲。

針對異步電機的彈性轉子振動問題，國內外學者已開展了深入研究。劉清等[1]建立了彈性轉子的非線性動力學模型，探討了系統受不平衡磁拉力作用時的主共振響應。Iwatsubo等[2]研究了三相異步電機轉子的參激振動特性，并給出了振動不穩定判據。寧建榮等[3]采用解析法揭示了彈性轉子的徑向電磁力分布規律，并采用數值法給出了對比驗證。Belmans等[4]利用Fourier級數建立了異步電機的彈性轉子動力學模型。需要指出的是，現有研究均采用慣性坐標系，通常采用多尺度法[5]、攝動法[6]和Chebyshev多項式[7]等進行近似求解。事實上，還可以在磁場同步坐標系下研究彈性轉子的振動穩定性問題。Canchi等[8]運用坐標變換原理研究了彈性環狀結構的面內振動穩定性。Singh等[9]在磁場同步坐標系下求解了多相異步電機的力矩方程。Nelson等[10]在磁場隨動坐標系下建立了異步電機的動力學模型，并分析了低轉速下的穩定性問題。本質上，同步坐標系可消除電機時變參數的影響，有利于解決由移動載荷產生的動力穩定性問題。

采用Hamilton原理在磁場同步坐標系下建立異步感應電機的外轉子橫向振動模型，通過經典振動理論分析基本機電參數對系統動力穩定性的影響，并分別采用Floquét和Runge-Kutta方法計算不穩定域和響應，從而驗證了解析結果的正確性。

1 動力學建模

1.1 坐標系建立

根據外轉子感應電機的結構特征，可將轉子簡化為旋轉薄殼狀彈性結構。圖1為異步電機的彈性外轉子動力學模型。圖1中，P(θ,t)為慣性坐標系下作用于轉子表面的單位面積磁拉力，該磁拉力以磁場同步轉速Ω(Ω=ω/p；ω為相電流頻率；p為極對數)勻速旋轉。o-rθ為慣性坐標系；uθ和vr分別為轉子的切向和徑向位移，該位移與空間角度θ和時間t有關；o-ρφ為磁場同步坐標系，該坐標系以磁場恒定轉速Ω同步旋轉，uφ和vρ分別為切向和徑向位移。轉子的轉速、軸向厚度、徑向寬度、中性圓半徑、材料密度、彈性模量、切向和徑向支撐剛度分別為Ωr、h、c、R、d、E、ku和kv。

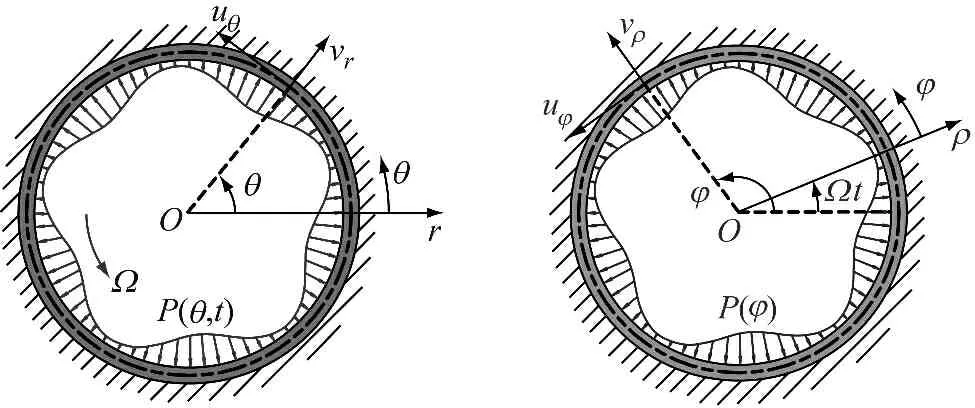
圖1 外轉子異步感應電機轉子坐標系

Fig.1 Coordinates frame of external rotor of asynchronous induction motor

1.2 數學建模

依據Hamilton原理建立磁場同步坐標系下轉子的彈性動力學方程。轉子的動能為

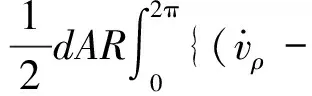
(1)

式中：A(A=ch)為截面積，且

轉子的勢能為

φ

(2)

式中：I(I=ch3/12)為主慣性矩，且

支撐勢能為

φ

(3)

式中:ku和kv分別為切向和徑向支撐剛度。轉子截面上，單位面積的磁拉力為[11-12]

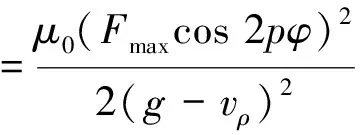
(4)

式中:μ0為真空磁導率;Fmax為最大磁動勢，且

(5)

式中:N為線圈匝數；Im為相電流；m為相數；y1為定子節距；z為定子齒數；g為平均氣隙長度。磁拉力做功可表示為

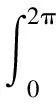
(6)

將式(4)、式(5)代入式(6)，可得

(1+cos 2pφ)dφ

(7)

根據Hamilton原理，有

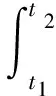
(8)

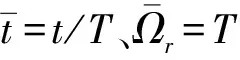
(9)

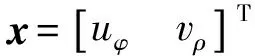
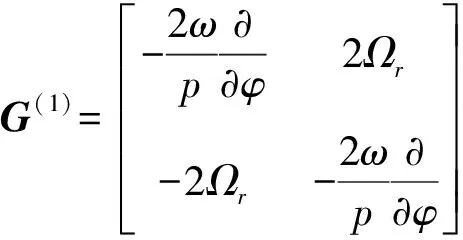
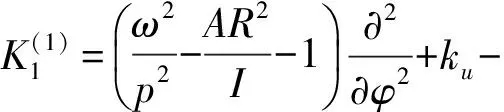
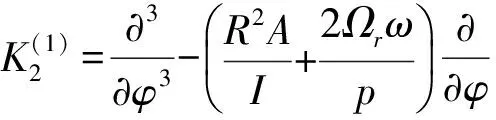
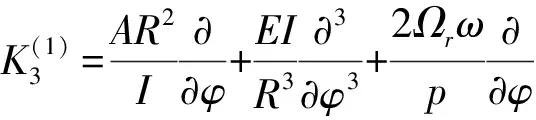
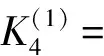
cos 2pφ),

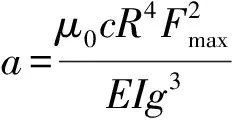
2 磁場同步坐標系分析

根據Galerkin方法，系統的一階響應可表示為[13]

(10)

式中:n為波數；i為虛數單位，cc表示共軛。定義內積

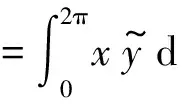
(11)

式中：“～”為復共軛。將式(10)代入式(9)，并與einφ作內積可得

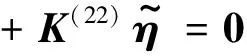
(12)

式中：

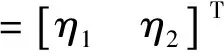
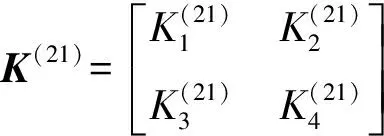
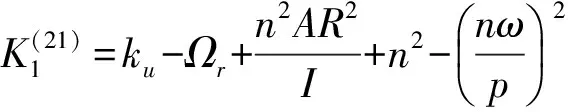
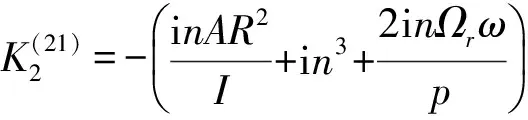
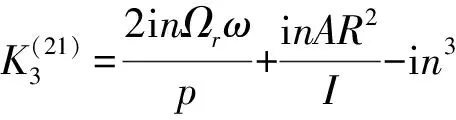
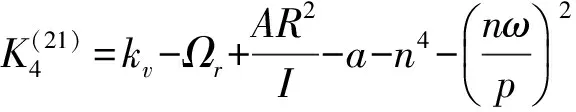
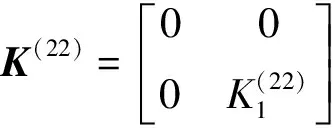
當波數與極對數不等時，系統將產生自由振動，可運用線性振動理論加以分析。本文重點研究波數與極對數相等時彈性轉子的振動穩定性問題。假設ηj(t)=xj+iyj(j=1，2)，式中xj和yj均為實變量，則式(12)可改寫為

(13)

式中:

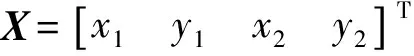
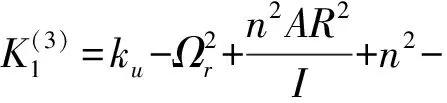
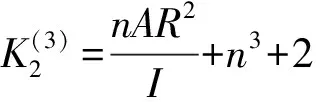
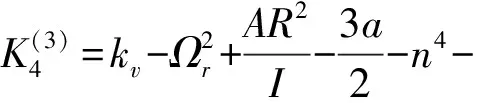
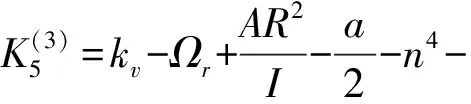
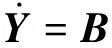
×Y

(14)

式中:

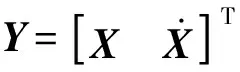
(B-λI)Y=0

(15)

式中:λ為特征值。

當特征值的實部大于零且虛部為零時,系統將產生發散不穩定；當特征值的實部大于零且虛部互為相反數時，系統將處于顫振不穩定狀態[14]。表1為感應電機外轉子的基本參數。

表1 基本參數

根據式(15)可得旋轉磁場的無量綱轉速為2.0時特征值隨機電參數的變化規律，如圖2所示。圖2中實線和虛線表示特征值的實部和虛部。圖2(a)和圖2(c)分別表示波數為2和3時，節距對特征值實、虛部的影響。根據不穩定性的判斷依據，節距可周期性地導致發散不穩定。波數的改變可顯著影響節距周期和不穩定區間。當波數為2時，周期為36，不穩定區間為(10.0，26.0)和(46.0，62.0)；當波數為3時，周期為24，不穩定區間為(5.0，19.0)、(29.0，43.0)和(53.0，67.0)。對于不同的振動波數，相電流對振動穩定性的影響規律，如圖2(b)和圖2(d)所示。波數不僅改變了不穩定區間，還影響了不穩定性質。當波數為2時，相電流可導致兩種不穩定，其中發散不穩定區間為(48.5，87.5)，顫振不穩定區間為(136.0，200)；當波數為3時，相電流僅導致發散不穩定，不穩定區間為(94.8，200)。

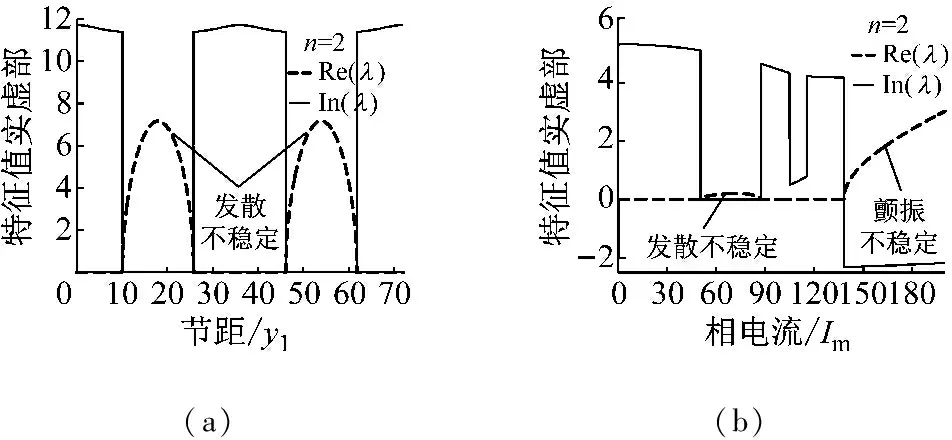
(a)(b)

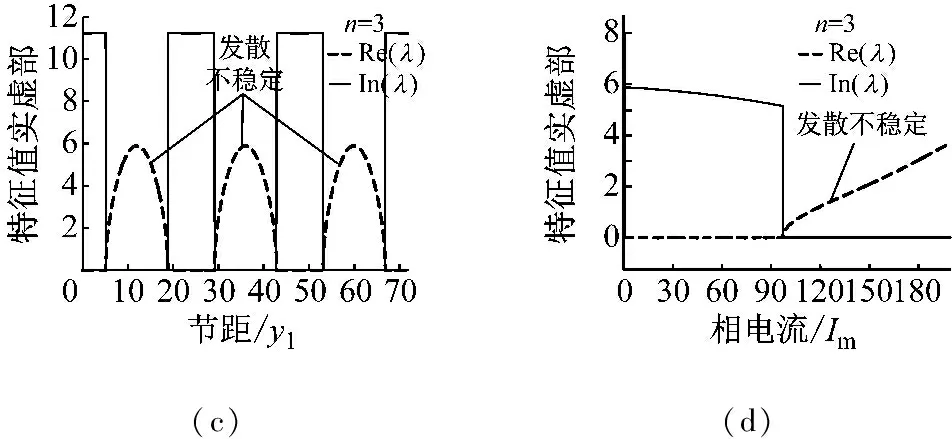
(c)(d)

圖2 基本機電磁參數對穩定性的影響

Fig.2 Influence of basic mechanical-electromagnetic parameters on stability

3 慣性坐標系分析

引入坐標變換θ=φ+Ωt，式(12)可改寫為

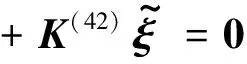
(16)

式中:

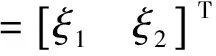
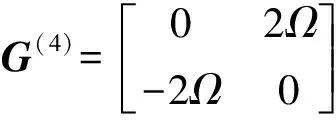
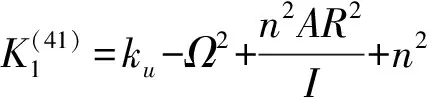
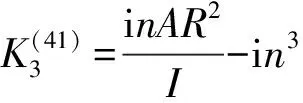
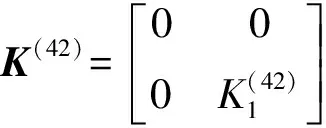
根據Floquét理論[15-16]，假設ξl=Al+iBl(l=1，2)，Al、Bl均為時間的實函數，式(16)可表示為

(17)

式中:

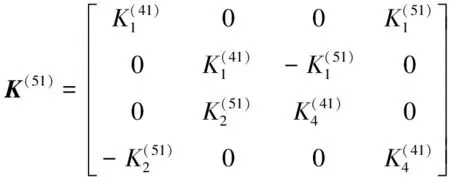
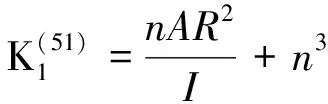
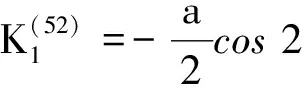
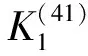
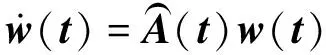
(18)

式中：

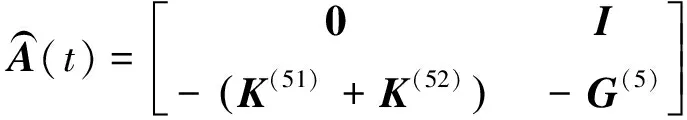
0和I分別為4×4階零矩陣和單位陣。

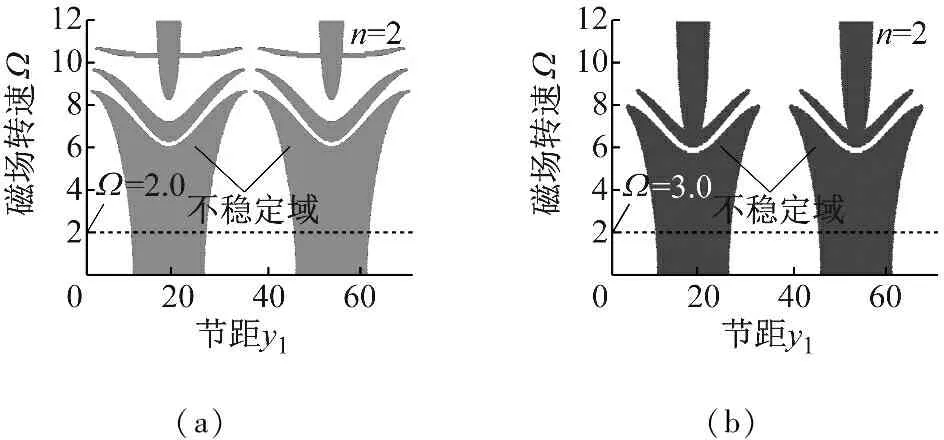
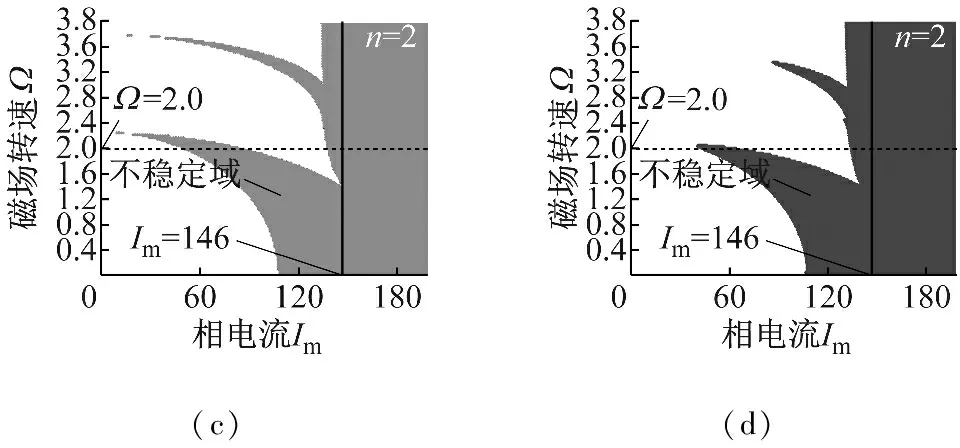
圖3描述了系統不穩定域的分布規律，其中圖3(a)和圖3(c)分別表示磁場同步坐標系下節距和相電流對不穩定域的影響；圖3(b)和圖3(d)分別描述了慣性坐標系下通過Floquét理論得到的不穩定域的分布規律。忽略計算精度的影響，兩種坐標系下的結果基本一致，驗證了磁場同步坐標系的正確性。此外，圖3(a)和圖3(b)表明節距可周期性地影響不穩定域的分布，該周期為36/n，當節距為72Y/n(Y為整數)時，系統處于恒穩定狀態。圖3(c)和圖3(d)表明隨著相電流的增加，電磁剛度逐漸增大，不穩定域逐漸變大，當相電流位于區間(0，146 A)時，不穩定域由兩個分支構成，而當相電流>146 A時，系統將完全失穩。需要指出的是，當磁場的無量綱轉速取值為2.0時(圖中虛線標注位置)，不穩定的變化規律與圖2一致，進一步驗證了磁場同步坐標系下解析結果的正確性。

(a)(b)

(c)(d)

圖3 基本機電磁參數對不穩定性的影響

Fig.3 Effect of basic mechanical-electromagnetic parameters on instability behaviors

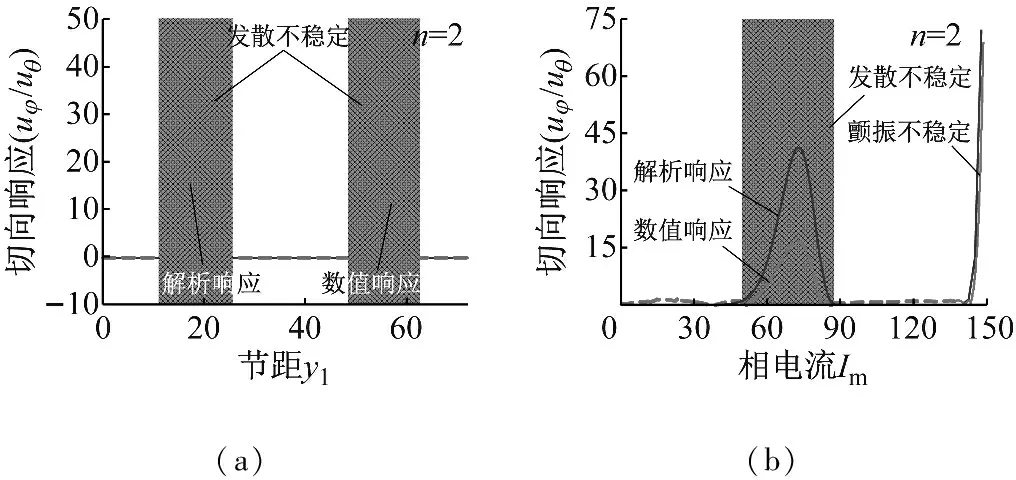
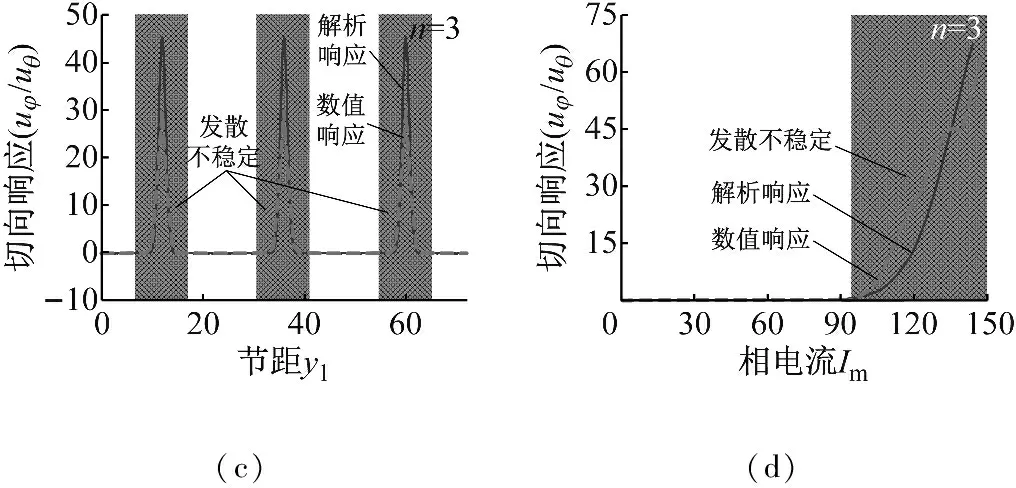
為驗證圖2和3結果的正確性，本節求解了100 s內切向響應隨節距和相電流等機電參數的變化規律，如圖4所示。圖中實線為隨動坐標系下的解析響應，虛線為基于Runge-Kutta方法的慣性坐標系下的數值響應，忽略計算誤差，兩種方法得到的結果基本一致。在穩定區間，響應為趨近于零的直線，而在不穩定區間，響應顯著大于零，與圖2和3的結果一致。由圖4(a)可知，節距周期性地影響切向響應，當節距為(36+72Y)/n(Y為整數)時，切向響應最大；由圖4(b)可知，當相電流處于發散不穩定區間(48.5 A，87.5 A)時，響應的增長速度顯著小于顫振不穩定區間(94.8 A，200 A)的響應。圖4(c)和圖4(d)描述了波數為3時，節距和相電流對切向響應的影響，經分析可得相似結論。

(a)(b)

(c)(d)

圖4 切向響應隨基本機電磁參數的變化規律

Fig.4 Tangential response versus basic mechanical-electromagnetic parameters

4 結 論

本文研究了異步感應電機的外轉子彈性振動穩定性問題，揭示了基本機、電和磁參數對穩定性的影響。主要工作和結論如下：

(1) 采用能量法建立了磁場同步坐標系下異步感應電機的外轉子彈性振動模型，并采用經典振動理論分析了動力穩定性問題。

(2) 根據所建動力學模型，計算了系統的特征值，揭示了動力穩定性與節距和相電流等基本機電參數的映射關系。

(3) 利用坐標變換得到了慣性坐標系下的參激振動模型，采用Floquét方法計算了不穩定域，該結果與解析結果一致。

(4) 采用Runge-Kutta方法計算了彈性外轉子的切向響應，進一步驗證了磁場同步坐標系下解析結果的正確性。

[1] 劉清，李琨，王肖鋒，等．不平衡磁拉力作用下電機柔性轉子非線性振動研究[J]．中國機械工程，2014，25(18)：2446-2450．

LIU Qing, LI Kun, WANG Xiaofeng, et al. Nonlinear vibration behavior of flexible rotors under unbalanced magnetic pull[J]. China Mechanical Engineering, 2014, 25(18): 2446-2450.

[2] IWATSUBO T, KAWAMURA S, HAYASHI Y, et al. Vibration analysis of an induction motor under electromagnetic force[J]. Transactions of the Japan Society of Mechanical Engineers, 2003, 69(680): 939-944.

[3] 寧建榮，夏加寬，劉佳男，等．三相異步電動機轉子偏心時徑向電磁力特性分析[J]．振動與沖擊，2016，35(2)：10-14．

NING Jianrong, XIA Jiakuan, LIU Jianan, et al. Analysis on electromagnetic force characteristic of three-phase induction motor under eccentricity[J]. Journal of Vibration and Shock, 2016, 35(2): 10-14.

[4] BELMANS R, VANDENPUT A, GEYSEN W. Influence of unbalanced magnetic pull on the radial stability of flexible-shaft induction machines[J]. Electric Power Applications, IEE Proceedings, 1987, 134(2): 101-109.

[5] ZHAO Z F, WANG S Y. Parametric instability induced by traveling magnetic load within permanent magnet motors[J]. Nonlinear Dynamics, 2015, 80(1): 827-843.

[6] 王世宇，陳東亮，劉建平，等．分組對稱旋轉周期結構固有頻率分裂解析分析[J]．天津大學學報，2012，45(5)：393-399．

WANG Shiyu, CHEN Dongliang, LIU Jianping, et al. Analytical analysis on natural frequency splitting of rotationally periodic structure with grouped features[J]. Journal of Tianjin University, 2012, 45(5): 393-399.

[7] SINHA S C, WU D H, JUNEJA V, et al. Analysis of dynamic systems with periodically varying parameters via Chebyshev polynomials[J]. ASME Journal of Vibration and Acoustics, 1993, 115(1): 96-102.

[8] CANCHI S V, PARKER R G. Parametric instability of a circular ring subjected to moving springs[J]. Journal of Sound and Vibration, 2006, 293(1/2): 360-379.

[9] SINGH G K, PANT V, SINGH Y P. Stability analysis of a multi-phase (six-phase) induction machine[J]. Computers and Electrical Engineering, 2003, 29(7): 727-756.

[10] NELSON R H, LIPO T A, KRAUSE P C. Stability analysis of a symmetrical induction machine[J]. IEEE Transactions on Power Apparatus and Systems, 1969, PAS-88(11): 1710-1717.

[11] YANG B S, KIM Y H, SON B G. Instability and imbalance response of large induction motor rotor by unbalanced magnetic pull[J]. Journal of Vibration and Control, 2004, 10(3): 447-460.

[12] 周順榮．電機學[M].北京:科學出版社，2007．

[13] 胡海巖．應用非線性動力學[M].北京:航空工業出版社，2000．

[14] COOLEY C G, PARKER R G. Mechanical stability of high-speed planetary gears[J]. International Journal of Mechanical Sciences, 2013, 69: 59-71.

[15] FARKAS M. Periodic motions[M]. New York: Springer-Verlag, 1994.

[16] MENG P. Parametric instability investigation and stability based design for transmission systems containing face-gear drives[D]. Knoxville: University of Tennessee, 2012.