慣質系數對車輛ISD懸架系統頻率特性的影響研究

楊曉峰， 杜 毅， 劉雁玲， 胡健濱， 劉昌寧， 徐 旭

(1. 江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013；2. 江蘇大學 理學院，江蘇 鎮江 212013)

慣容器是一種新型質量元件，作用于它兩端點的力正比于兩個端點相對加速度[1]，在各種機械隔振系統中使用慣容器能提升性能的事實已經得到了廣泛證實[2-6]。通過將慣容器引入車輛懸架系統，對車輛懸架理論的研究產生了積極而深遠的影響。研究表明[7-14]，對比傳統懸架，應用慣容器的車輛懸架隔振性能得到明顯提升。

在振動系統中，彈簧可以儲存能量，提供靜支撐，并且決定系統固有頻率。阻尼器可以耗散能量，限制共振點的振幅。慣容器作為一種機械元件，也可以儲存能量。根據元件的串并聯關系，按照排列組合的方式，彈簧、阻尼和慣容器可以組成多種ISD(Inerter Spring Damper)懸架結構。在文獻[15]中，僅僅以慣容器和彈簧并聯的單自由度、二自由度和多自由度簡單隔振系統為對象，研究了慣質系數變化對系統主頻的影響，同時分析了系統主頻對不同位置慣容器慣質系數的敏感程度。然而，對于慣質系數對各類ISD懸架系統偏頻和主頻特性的作用規律，還沒有做過深入研究。

本文結合被動機械元件工作特點和元件排列組合方式，列出了10種可行的ISD懸架。在無阻尼自由振動情況下，根據無阻尼阻抗，將ISD懸架分成4類懸架，對其中3類含有慣容器的懸架進行深入研究分析。建立懸架動力學模型，推導并分析懸架的偏頻和主頻,研究慣質系數變化對這3類懸架系統偏頻和主頻特性的影響及其作用規律。

1 理論分析

1.1 機械阻抗理論

20世紀30年代初，通過機電比擬的方法提出來了機械阻抗方法的概念。機械阻抗被定義為各種激振頻域下響應量和激振量的比值。數學上，阻抗與導納互為倒數關系。慣容器的動力學表達式

(1)

式中：f為施加于元件兩端點上等大反向的力；v1，v2為慣容器兩端點的速度；b為慣質系數。

根據機械阻抗的定義，彈簧、阻尼和慣容器元件的機械阻抗表達式，如表1所示[16]。

表1 元件機械阻抗表達式

表1中：s為拉氏變換復變量；k為彈簧剛度；c為阻尼系數。

由n個阻抗為Yi的元件并聯而成的系統等效阻抗Yp和由n個阻抗為Yi的元件串聯而成的系統等效阻抗Ys表達式如下所示

(2)

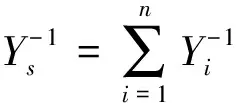
(3)

1.2 ISD懸架及其阻抗

由于慣容器和阻尼是機械元件，必須處于有效的位置和行程范圍內，否則元件會過載。因此車輛懸架內部的慣容器和阻尼必須要有彈簧的支撐，才能保證各元件的正常的工作，發揮各自的效果[17]。根據上述原理，并結合排列組合方式，圖1左側給出了10種可行的ISD懸架。

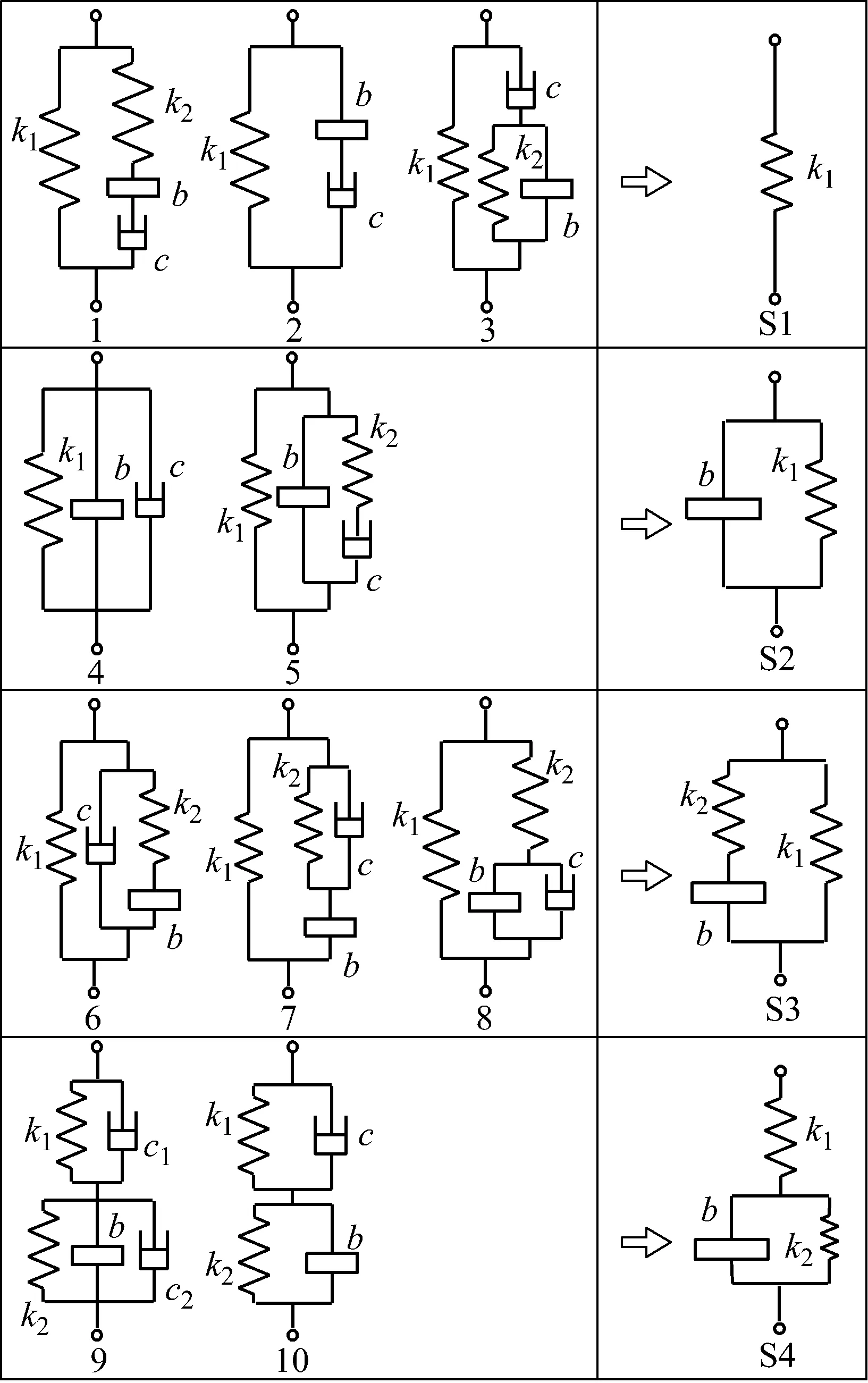
圖1 10種ISD懸架及其無阻尼退化結構

根據機械阻抗以及串、并聯系統的阻抗特性，可得圖1中10種懸架的速度型機械阻抗，其中結構1、2、……、10對應的阻抗傳遞函數分別為Y1(s)、Y2(s)、……、Y10(s)

(4)

(5)

(6)

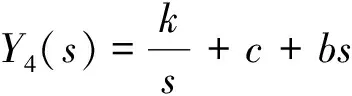
(7)

(8)

(9)

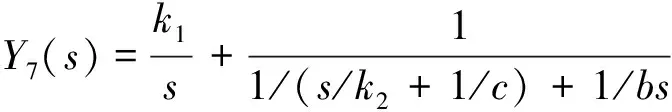
(10)

(11)

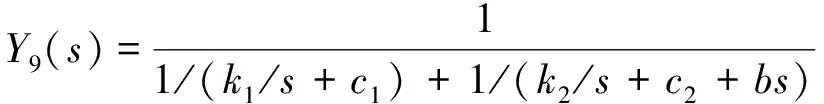
(12)

(13)

無阻尼自由振動時，懸架中阻尼為零，各個懸架的阻抗退化。將無阻尼阻抗相同的懸架歸為一類，如表2所示。

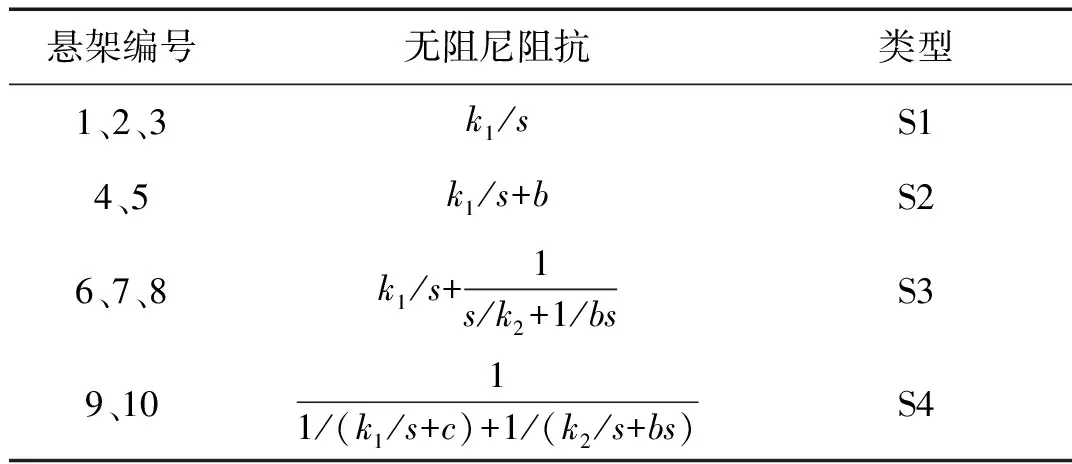
表2 懸架分類

從無阻尼阻抗的表達式結構可以推出這類懸架的結構，圖1種的10種ISD懸架結構退化成左側的4種類型。由于退化的S1型懸架結構就是傳統被動懸架的無阻尼結構，已經得到了充分研究，因此下文只對S2、S3、S4型懸架進行分析研究。

2 偏頻與主頻的推導

2.1 懸架系統動力學模型

應用復頻域懸架阻抗法建立1/4模型，如圖2所示。

從圖2可知，1/4車輛懸架模型拉普拉斯變換下的動力學方程為

(14)

式中：mu為簧下質量；ms為簧上質量；zr為路面隨機輸入；zs，zu分別為簧上、簧下質量垂直位移；Zr，Zs，Zu分別為zr，zs，zu的拉氏變換形式；kt為輪胎剛度；Y(s)為復頻域懸架阻抗。

2.2 推導過程

無阻尼自由(Zr=0)振動時，對于S2型懸架，計算方法如下。

2.2.1 車身偏頻推導

將S2型懸架的阻抗表達式代入表達式(14)中，同時令mu不動(Zu=0)，即

(15)

顯然，對于S2型懸架，車身偏頻ω0是關于慣質系數b的單調減函數。

2.2.2 車輪偏頻推導

將S2型懸架的阻抗表達式代入表達式(14)中，同時令ms不動(Zs=0)，即

(16)

顯然，對于S2型懸架，車輪偏頻ωt也是關于慣質系數b的單調減函數。

2.2.3 主頻計算

設兩個質量以相同的圓頻率ω和相位角φ作簡諧振動，振幅為zs0和zu0，則其解為zs=zs0ej(ωt+φ),zu=zu0ej(ωt+φ)，將zs和zu代入式(4)，化簡計算得

(17)

此方程組要有非零解的條件是zs0和zu0的系數行列式為零，即

Δ(ω)=(msmu+msb+mub)ω4-

(muk+mskt+bkt+msk)ω2+kkt=0

(18)

式中：p=msmu+msb+mub+b2，q=muk+mskt+bkt+msk

ω1、ω2根式的分母中慣質系數b的最大次數為二次，而分子慣質系數b的最大次數為一次，因此對于S2型懸架，主頻ω1、ω2也都是關于慣質系數b的減函數。

對于S3、S4這兩類懸架的偏頻和主頻，用相同的計算方法分別進行推導，具體內容從略。將各類懸架計算所得的懸架偏頻和主頻數目整理，如表3所示。由表3各類懸架偏頻和主頻的數目得出，不同類型的懸架會造成偏頻與主頻數目的差異。

3 仿真分析

3.1 慣質系數對偏頻和主頻數值的影響

為研究S2、S3和S4型懸架中慣質系數對偏頻和主頻的影響，比較分析總結規律，利用車身1/4懸架模型，在MATLAB環境下進行數值仿真。同時在仿真圖像3、4、5中加入了傳統被動懸架的偏頻和主頻作為參考進行比較。傳統被動懸架的彈簧剛度與表中懸架主彈簧剛度數值一致，簧載質量、非簧載質量和輪胎剛度與表4中的參數保持一致。

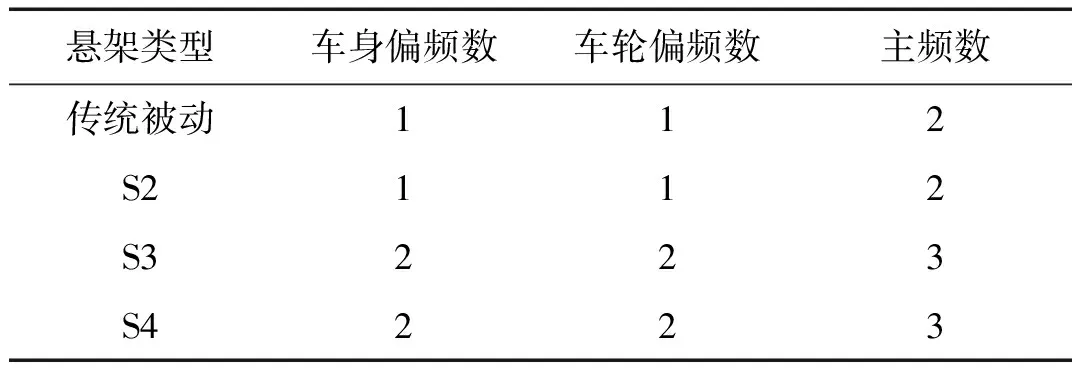
表3 懸架偏頻主頻數目

表4 系統參數

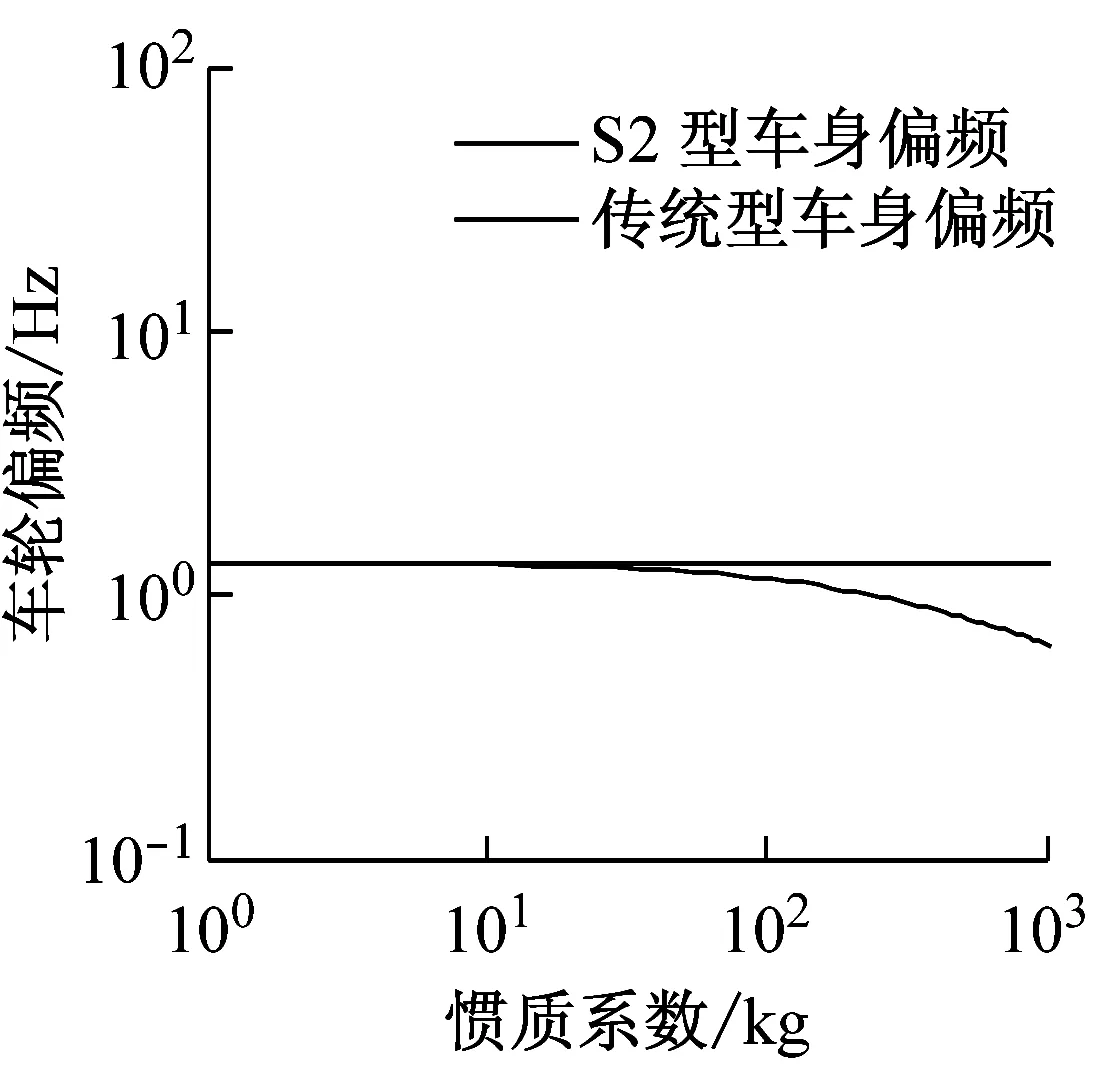
由圖3可知，在慣質系數非零的情況下，S2型懸架的偏頻和主頻都始終小于傳統型懸架對應的偏頻和主頻。因此，S2型懸架在降低固有頻率方面較為顯著。同時，S2型懸架的偏頻和主頻始終隨著慣質系數的增加不斷下降。

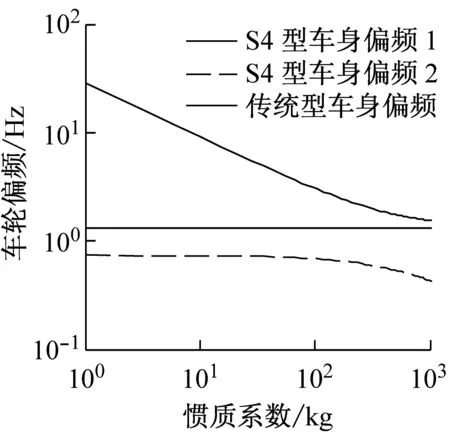
由圖4和圖5可知，S3和S4型圖像特性類似。車身和車輪偏頻分別位于傳統型懸架車身和車輪偏頻的兩側，主頻分別位于傳統型懸架兩個主頻的三側。隨慣質系數增加，車身偏頻、車輪偏頻和主頻也都不同程度地在下降。同時，最大的偏頻和主頻在慣質系數達到一定數值時，就趨近于傳統被動懸架的偏頻和數值最大的主頻。

總結圖3、圖4和圖5中的圖像特性，慣質系數確實能夠有效降低S2、S3和S4型懸架的偏頻和主頻。

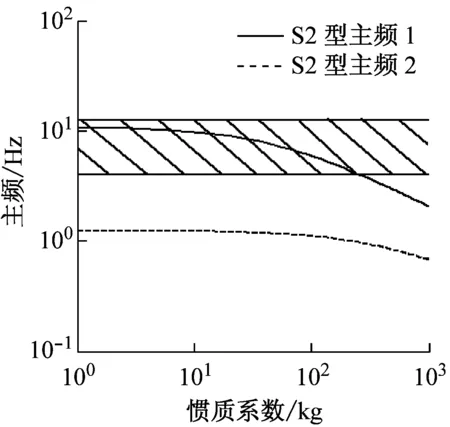
進一步研究主頻，圖6中陰影區域為4.0～12.5 Hz，為垂直方向人體最敏感的頻率范圍。隨著慣質系數增加，S2型慣質系數超過300 kg，S3型慣質系數超過20 kg，S4型慣質系數超過50 kg后，使得懸架主頻脫離人體敏感范圍。也就說明了ISD懸架能夠通過增加慣質系數，降低懸架自身主頻，來使得懸架自身主頻小于垂直振動敏感頻率，從而改善汽車乘坐的舒適性。

3.2 慣質系數對偏頻和主頻的影響程度分析

保持表4種參數不變，通過觀察在不同慣質系數條件下，增加1 kg慣質系數引起的S2、S3和S4類懸架偏頻和主頻的降幅。從而反映出在不同慣質系數條件下，慣質系數對偏頻和主頻的影響程度。

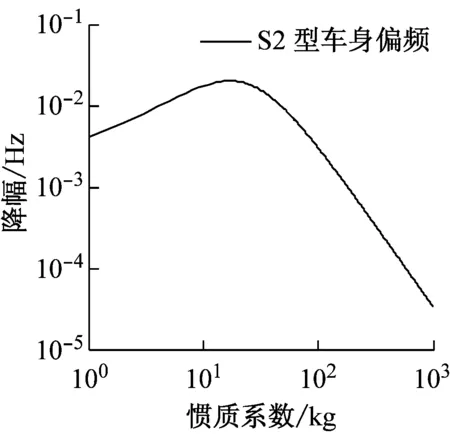
由圖7可知，對于S2型懸架，在1～10 kg范圍內，增加單位慣質系數引起的偏頻和主頻的降幅略有上升。而當慣質系數<10 kg后，偏頻和主頻的降幅隨著慣質系數增加而下降。即隨著慣質系數增加，慣質系數對偏頻和主頻的影響程度不斷下降。

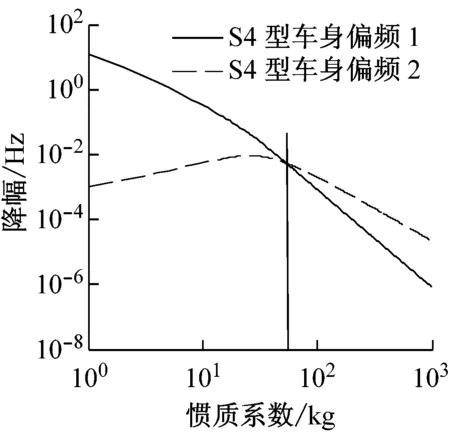
由圖8和圖9可知，S3和S4型懸架的特性類似，隨著慣質系數增加，降幅基本呈現下降趨勢。同時也能發現，在車身偏頻和車輪偏頻圖像中，當慣質系數位于黑線左側時，最大的偏頻(車身偏頻1和車輪偏頻1)降幅最大。而當慣質系數位于黑線右側時，最小的偏頻(車身偏頻2和車輪偏頻2)降幅最大，同理主頻圖像也有類似特性。由此得出，在不同的慣質系數范圍內，偏頻和主頻的降幅不同，即慣質系數對不同的偏頻和主頻的影響程度不同。

總結圖7、圖8和圖9，雖然慣質系數能夠有效降低S2、S3和S4型懸架偏頻與主頻，但隨著慣質系數的增加，慣質系數對偏頻與主頻的影響程度不斷下降。而且對于S3和S4類懸架，不同慣質系數數值區間內，慣質系數對不同的偏頻和主頻影響程度也不同。

4 結 論

(1)運用機械阻抗法，建立懸架動力學模型，推導并分析阻抗，分類研究ISD懸架的偏頻和主頻是一種有效的方法。

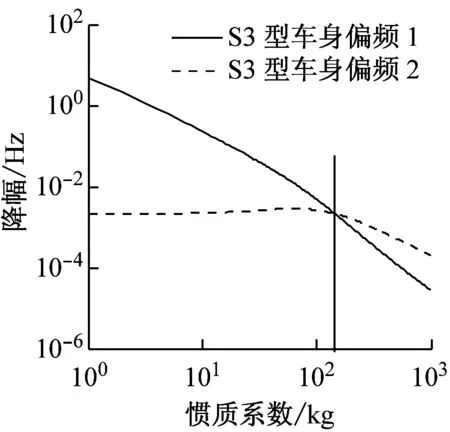
圖8 S3型固有頻率的降幅

Fig.8 The decreasing amplitude of natural frequencies of suspension S3

(2)由于慣容器質量阻抗的引入和新型機械網絡拓撲特性的影響，使得不同類型ISD懸架系統偏頻和主頻數目有差異。

(3)增加慣質系數能有效降低S2、S3和S4型懸架偏頻與主頻，使得主頻脫離垂直方向人體最敏感的頻率范圍。同時慣質系數對偏頻與主頻的影響程度隨著慣質系數的增加而減小。

[1] SMITH M C. Synthesis of mechanical networks: the inerter[J]. IEEE Transactions on Automatic Control, 2003, 47(10):1657-1662.

[2] CHEN M Z Q, PAPAGEORGIOU C, SCHEIBE F, et al. The missing mechanical circuit element[J]. IEEE Circuits and Systems Magazine, 2009, 9(1):10-26.

[3] JIANG J Z, MATAMOROS-SANCHEZ A Z. Passive suspensions incorporating inerters for railway vehicles[J]. Vehicle System Dynamics, 2012, 50(1):263-276.

[4] LIMEBEER D J N, SHARP R S. Bicycles, motorcycles, and models[J]. IEEE Control Systems, 2006, 26(5):34-61.

[5] WANG F C, HONG M F, CHEN C W. Building suspensions with inerters[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 1989-1996, 2010, 224(8):1605-1616.

[6] HANAZAWA Y, SUDA H, YAMAKITA M. Analysis and experiment of flat-footed passive dynamic walker with ankle inerter[C]// IEEE International Conference on Robotics and Biomimetics. IEEE, 2011:86-91.

[7] SMITH M C, WANG F C．Performance benefits in passive vehicle suspensions employing inerters[J]. Vehicle System Dynamics, 2004, 42(4): 235-257.

[8] 葛正, 王維銳. 車輛主動慣容式動力吸振懸架系統研究[J]. 振動與沖擊, 2017，36(1):167-174.

GE Zheng, WANG Weirui. Vehicle active ISD-DVA suspension system[J]. Journal of Vibration and Shock, 2017，36(1):167-174.

[9] SHEN Y, CHEN L, YANG X, et al. Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension[J]. Journal of Sound & Vibration, 2016, 361:148-158.

[10] WANG R, YE Q, SUN Z, et al. A study of the hydraulically interconnected inerter-spring-damper suspension system[J]. Mechanics Based Design of Structures and Machines, 2016:1-15.

[11] 杜甫, 毛明, 陳軼杰,等. 基于動力學模型與參數優化的ISD懸架結構設計及性能分析[J]. 振動與沖擊, 2014, 33(6):59-65.

DU Fu, MAO Ming, CHEN Yitie, et al. Structure design and performance analysis of inerter-spring-damper suspension structure based on dynamic model and parameter optimization[J]. Journal of Vibration and Shock, 2014, 33(6):59-65.

[12] 陳龍, 張孝良, 江浩斌, 等. 基于機電系統相似性理論的蓄能懸架系統[J]. 中國機械工程, 2009, 20(10):1248-1251.

CHEN Long, ZHANG Xiaoliang, JIANG Haobin, et al. Vehicle suspension system employing inerter based on electrical-mechanical analogy theory[J]. China Mechanical Engineering, 2009, 20(10):1248-1251.

[13] 陳龍, 張孝良, 聶佳梅, 等. 基于半車模型的兩級串聯型ISD懸架性能分析[J]. 機械工程學報, 2012, 48(6):102-108．

CHEN Long, ZHANG Xiaoliang, NIE Jiamei, et al. Performance analysis of two-stage series-connected inerter-spring-damper suspension based on half-car model[J]. Journal of Mechanical Engineering, 2012, 48(6):102-108.

[14] ZHANG X J, AHMADIAN M, GUO K H. On the benefits of semi-active suspensions with inerters[J]. Shock and Vibration, 2012, 19(3):257-272.

[15] CHEN M Z Q, HU Y, HUANG L, et al. Influence of inerter on natural frequencies of vibration systems[J]. Journal of Sound and Vibration, 2014, 333(7):1874-1887.

[16] 陳龍, 楊曉峰, 汪若塵, 等. 基于二元件ISD結構隔振機理的車輛被動懸架設計與性能研究[J]. 振動與沖擊，2013, 32(6):90-95.

CHEN Long, YANG Xiaofeng, WANG Ruochen, et al. Design and performance study of vehicle passive suspension based on two-element inerter-spring-damper structure vibration isolation mechanism[J]. Journal of Vibration and Shock, 2013, 32(6): 90-95.

[17] 陳龍, 楊曉峰, 汪若塵, 等. 改進的ISD三元件車輛被動懸架性能的研究[J]. 汽車工程, 2014, 36(3):340-345.

CHEN Long, YANG Xiaofeng, WANG Ruochen, et al. A study on the performances of vehicle passive suspension with modified inerter-spring-damper three-element structure[J]. Automotive Engineering, 2014, 36(3):340-345.