考慮強度退化的車輛主動輪可靠性靈敏度分析

劉 喆， 陶鳳和， 賈長治， 牟鵬博

(1.68129部隊，蘭州 730060； 2.軍械工程學院 火炮工程系，石家莊 050003； 3.裝甲兵學院 裝備運用系，安徽 蚌埠 233050)

履帶車輛是現代戰爭中十分重要的地面火力武器裝備，具有機動性好、火力猛、高新技術含量高和生存力強的獨特優勢，在難以計數的戰爭中主要起著火力打擊作用，可以快速構筑發射場地形成火力壓制，同時迅速撤出發射場地，躲避敵軍武器打擊，同時還可以為己方人員和重型坦克提供火力支援，在信息化、機械化的戰場環境中發揮著越來越重要的作用。

履帶車輛傳動系統的主動輪主要負責將發動機的動力傳遞到履帶板從而帶動整體車輛運動，是十分重要的傳動部件。可靠度是衡量機械系統質量的重要指標[1]，研究如何快速準確分析機械系統的可靠性，進而對其可靠性進行的優化設計研究具有十分重要的意義[2-4]。

進行機械零部件可靠性分析的研究模型應用最多是應力—強度模型，它是基于概率統計方法對機械系統的可靠度進行度量，為現代可靠性分析和機械系統結構優化設計做了較好的鋪墊。Lewis等[5-7]在運用應力—強度干涉模型研究可靠性問題時，將載荷作用過程用隨機性模型表示，符合實際情況，但研究時卻假設構件強度為確定值或者服從分布已知的概率函數，導致計算結果偏大。工程實際中，機械零部件由于載荷作用、內部微應力改變、材料本身缺陷等原因，其構件強度是隨著工作時間增加而逐漸下降的[8-9]，所以在進行可靠度分析時將零部件的強度也作為一種逐漸減小的隨機過程來計算將會更加符合工程實際情況。

機械零部件的可靠性靈敏度分析，是在可靠性分析的基礎上進行的零部件隨機參數的敏感性分析，分析結果可以評價機械零部件隨機參數的改變對其結構可靠性的影響程度[10]。機械零部件的可靠性靈敏度分析方法主要有基于矩理論方法和數值仿真模擬法的可靠性靈敏度分析方法[11]。進行機械可靠性的靈敏度分析對于其結構的可靠性設計、可靠性優化和定壽命可靠性設計等方面都有十分重要的應用前景[12]。

本文在可靠性理論中應力—強度干涉模型的基礎上，考慮機械系統零部件強度隨時間存在退化的情況，將機械部件的強度退化用Gamma隨機過程來近似模擬，運用可靠性設計的隨機攝動法、四階矩理論和靈敏度分析方法討論了履帶車輛傳動系統主動輪的可靠性靈敏度分析問題。在機械零部件隨機參數變量概率分布特性已知的條件下，可以迅速的獲得主動輪各隨機參數變量對其可靠度的靈敏度規律，從而為主動輪的可靠性設計、加工制造和使用維護提供科學準確的信息，為其可靠性優化設計做一定的探索和鋪墊，研究方法可以應用到其他機械產品上，有較好的適用性。

1 可靠性設計的攝動法

運用概率論分析設計方法，在機械系統的可靠性設計時考慮各設計變量的隨機性，確定基本的設計約束條件，建立交互設計模型等，是機械設計理論面臨的基本問題。可靠性設計攝動法可以準確的提供機械系統零部件的固有可靠性，提供可以進行實際工程計算的數學模型，分析零部件在工況條件下的可靠性，給出機械可靠性的設計方法。

要計算機械系統零部件的可靠度或者失效概率，需要明確零部件各隨機參數的概率密度函數或聯合概率密度函數，工程實際中，有很多基本隨機變量，如零部件強度和承受載荷等都是很多基本隨機變量的函數，這時如果計算其聯合概率分布函數又必須知道所有基本隨機變量各自的分布函數。但是在工程實際中往往沒有足夠的信息去確定它們，即使近似的指定其分布，知道其分布函數，通常也很難用多重積分算出零部件的可靠度或者失效概率。

當隨機變量的概率分布函數未知，只能通過數據資料計算獲得其前四階矩時，可以通過可靠性設計攝動法計算得到機械構件的可靠性指標，從而計算得到構件的可靠度或失效概率值。

零部件隨機參數的向量X和其狀態函數g(X)分別如下

X=Xd+εXp

(1)

g(X)=gd(X)+εgp(X)

(2)

式中：ε為一個參數；下標d為隨機參數變量中的確定部分；下標p為隨機參數變量中的隨機部分，均值為零，且隨機部分遠小于確定部分。

由攝動關系理論和相應的隨機分析理論，推導整理機械零部件狀態函數g(X)的均值、方差、三階矩和四階矩的表達式分別為

(3)

(4)

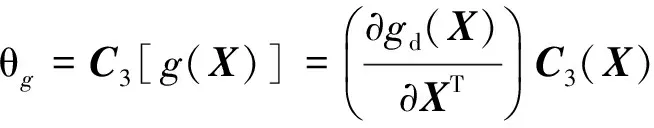
(5)

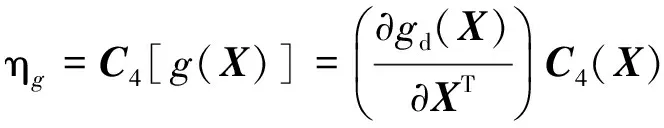
(6)

式中：Var(X)，C3(X)，C4(X)為隨機參數的方差、三階矩和四階矩向量；(·)[k]=(·)[k-1](·)=(·)?(·)?…?(·)為(·)的Kronecker冪，符號?代表Kronecker積，定義為(A)m×n?(B)p×q=[aijB]mp×nq。

將機械零部件的狀態函數g(X)對其隨機變量的向量X求偏導數如下所示

(7)

將式(7)代入式(4)～式(6)，可以得到零部件狀態函數相應的表達式。

矩方法是進行可靠性分析時十分實用的方法之一，應用矩方法可以很有效的對機械系統零部件進行可靠性分析，已知基本隨機參數的前兩階矩時，機械零部件可靠性指標的數學定義為

(8)

式中：βSM為標準化坐標系中原點至曲面切平面的最短距離。

如果機械零部件的各個隨機參數服從正態分布，則可以獲得其可靠度的估計量為

RSM=Φ(βSM)

(9)

式中：Φ(·)為標準的正態分布函數。

如果已知零部件基本隨機參數的前四階矩，其可靠性指標定義為

(10)

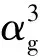
要計算可靠度或失效概率，需要知道概率密度函數或聯合概率密度函數。但在工程實際中很難有足夠的數據資料來確定它們的。因此，當概率密度函數未知，只能確定它們的前四階矩(即均值、方差、三階矩和四階矩)時，可以采用四階矩理論計算零部件的可靠性指標βFM，進而可以計算得到機械零部件的可靠度估計量RFM為

RFM=Φ(βFM)

(11)

工程實際計算時，前四階矩已經可以很準確的逼近隨機參數的真實分布情況，而且隨機參數的N(N>4)階矩是難于獲取的。

2 Edgeworth級數

機械零部件各隨機參數并不都服從正態分布，如果運用上式計算，可能會得到不準確甚至錯誤的結果，而運用Edgeworth方法可以將不服從正態分布的隨機變量隨機展開成標準的正態分布形式，進而便于進行可靠性分析計算，將隨機變量y近似展如下所示

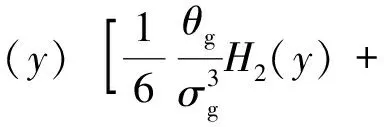
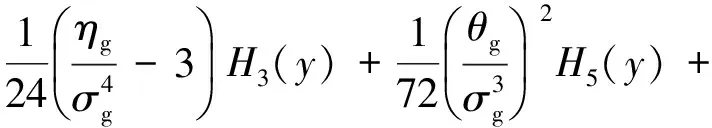
(12)

式中：φ為標準正態分布的概率密度函數；HJ-1為Hermite多項式，且

Hj+1(y)=yHj(y)-jHj-1(y)

H0(y)=1

H1(y)=y

(13)

這時，機械零部件的可靠度R可以運用下式來計算

R(β)=P[g(X)>0]=1-F(-β)

(14)

由于計算時只取Edgeworth級數的前四項，計算結果有時會出現零部件可靠度>1的錯誤情況，這時可以運用下面的修正公式來計算機械零部件的可靠度

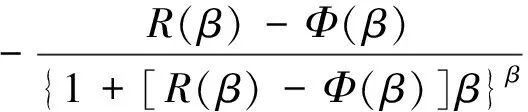
(15)

3 基于Gamma過程的強度退化

機械零部件的強度服從隨著時間t增大而逐漸退化的函數，針對某個具體零部件在任一時刻來說，強度退化量的數值大小是不確定的，即強度退化過程是時間t的隨機過程；且強度退化是單向的，零部件抵抗應力作用的能力是逐漸降低的，即機械零部件的強度退化具有單調性。

Gamma過程是一個具有獨立的非負增量隨機過程，且服從同一尺寸參數，能夠較好的擬合機械零部件強度的退化過程。

Gamma過程的數學模型為：假設所有參數隨機變量服從形狀參數ν>0和尺寸參數u>0的Gamma分布，其概率密度函數為

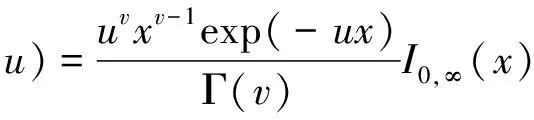
(16)

1)X(0)=0且概率為1；

2)X(τ)-X(t)～Ga(xv(τ)-v(t),u)，?τ>t≥0；

3)X(t)具有獨立的增量。

X(t)代表t時刻機械零部件強度的退化量，由Gamma過程函數的數學模型可知，X(t)的概率密度函數為fX(t)(x)=Ga(xv(t),u)，其均值和方差的計算公式如下

(17)

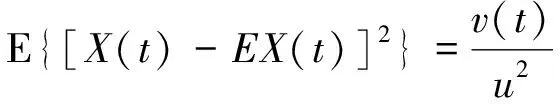
(18)

經過分析計算可知(對比參考文獻[4])，時刻t的期望劣化數值與指數成正比，即

∝tb

(19)

式中：b，c，u為Gamma過程的參數，其具體值可以通過統計理論運用最大似然法估計法獲得。

4 可靠性靈敏度分析

機械系統零部件的可靠度對其隨機參數均值和方差的靈敏度可以通過求偏導的方法計算

(20)

(21)

φ(βFM)

(22)

(23)

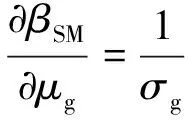
(24)

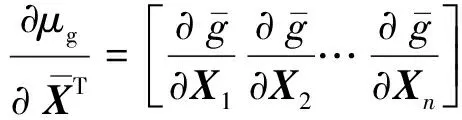
(25)

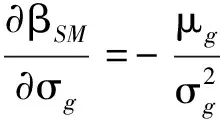
(26)

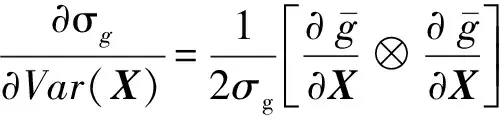
(27)

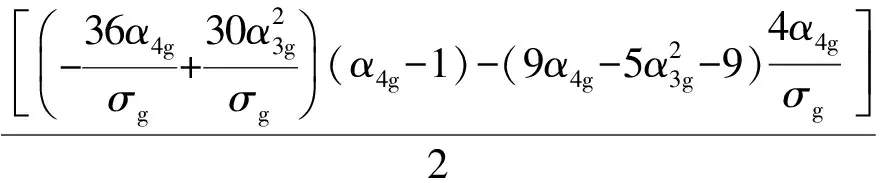
(28)

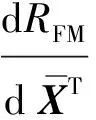
5 數值算例

為驗證本文分析計算方法的適用性，以履帶車輛底盤傳動系統的主動輪為例進行計算。履帶底盤系統主動輪是其傳動系統中重要的傳動部件之一，它將發動機的動力經過側減速器系統傳遞到履帶系統，通過輪齒的齒圈與履帶板嚙合，撥動履帶運動，從而推動履帶車輛整體前進或者后退，運行過程中只承受扭矩載荷，如圖1和圖2所示。

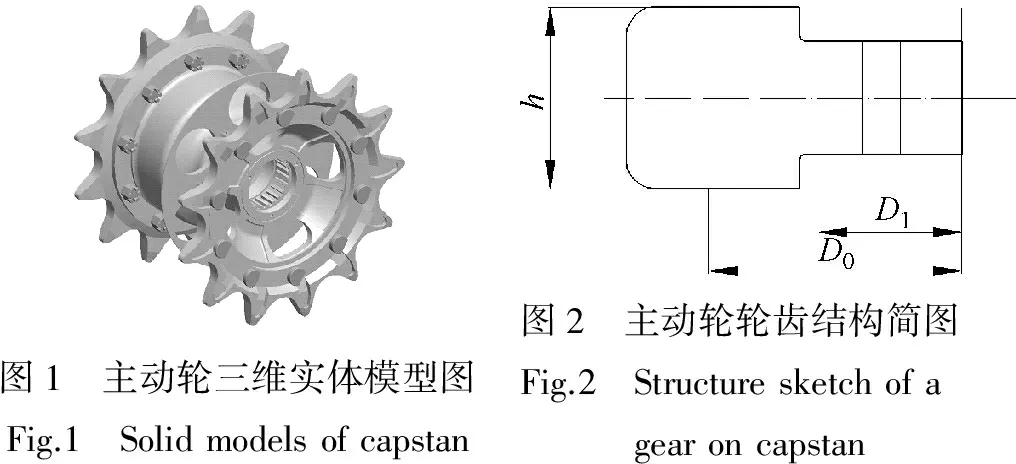
圖1 主動輪三維實體模型圖Fig．1 Solidmodelsofcapstan 圖2 主動輪輪齒結構簡圖 Fig．2 Structuresketchofagearoncapstan

若已知主動輪所傳遞的扭矩為P，危險截面處的直徑為D1，分度圓處直徑為D0，主動輪厚為h，各個參數的統計數值在表1中給出，Gamma過程的參數分別取為u=5，b=0.5，c=0.4，應用可靠性應力—強度干涉模型對主動輪進行可靠性靈敏度分析。

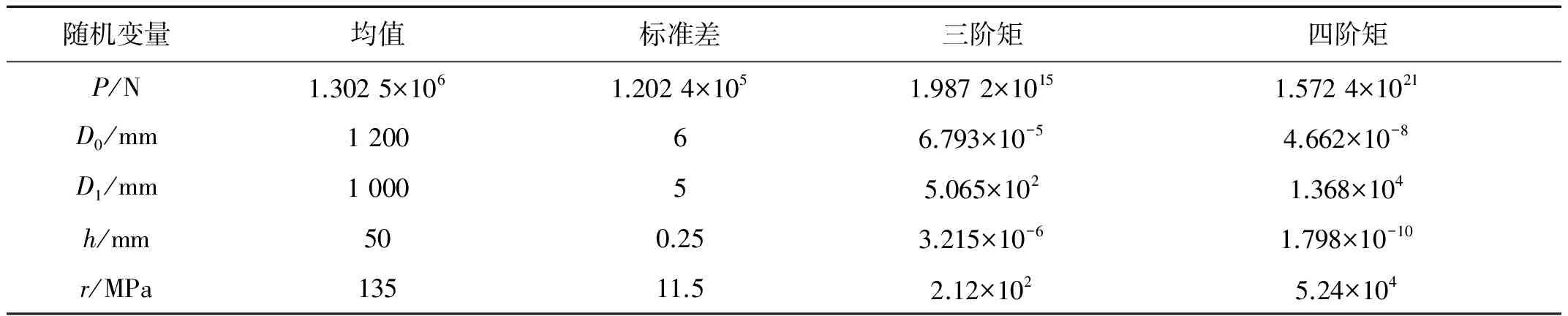
表1 隨機變量的統計特性

根據巴赫法，將主動輪的輪齒采用懸臂梁結構模型進行簡化，可以求得在D1直徑處為危險應力截面，且此處的切應力值為

(29)

則考慮強度隨時間退化情況的應力極限狀態方程可以表示為

g(X)=r(t)-τ

(30)

式中：r(t)為t時刻主動輪結構許用強度隨時間退化后的值，其均值、方差等可以運用Gamma隨機過程函數計算得到；基本隨機變量參數向量為

X=(bcuD0D1hP)T

主動輪的可靠度計算結果，如圖3曲線所示。圖3對比了四階矩方法和Monte-Carlo數值模擬方法的計算結果，從圖3可知，這兩種方法的計算結果比較接近，故運用四階矩理論計算考慮強度退化主動輪的可靠度，其計算結果是可以接受的，可靠度的變化規律符合工程實際情況。

圖4和圖5分別為主動輪可靠度對其各個隨機參數均值和方差的靈敏度變化曲線。

從圖4和圖5可知，隨著主動輪許用扭轉強度r、幾何尺寸D1和h均值的增加而可靠度增加，而主動輪承受的扭矩載荷P和幾何尺寸D0均值的增加將使主動輪可靠性降低；可靠度的變化率最大為主動輪的輪齒厚度h，其次依次為危險截面直徑D1，分度圓直徑D0，主動輪的許用扭轉強度r，最小的為主動輪承受的扭矩載荷總和P，即令主動輪趨于更加可靠(或使其失效)的速度大小排序為幾何尺寸、材料強度和載荷；靈敏度的絕對值都隨時間而逐漸增大，各參數方差的增加都會使主動輪趨于更加不可靠(失效)。

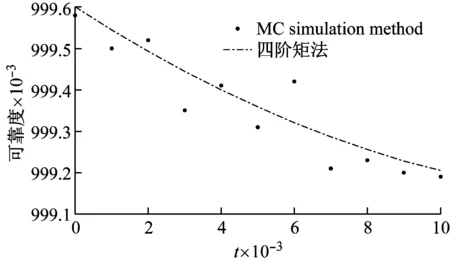
圖3 強度退化的主動輪可靠度曲線

圖4 主動輪對隨機參數均值的靈敏度曲線

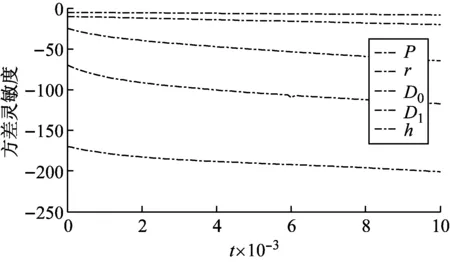
圖5 主動輪對隨機參數方差的靈敏度曲線

圖6為傳動系統主動輪可靠度對Gamma隨機過程參數的靈敏度變化曲線。

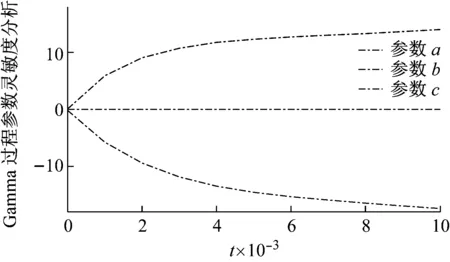
圖6 可靠度對Gamma過程參數的靈敏度

從圖6可知，Gamma隨機過程參數的靈敏度在初始時刻都比較小，隨著時間的增加，參數b，c對可靠度的影響在逐步增大。

6 結 論

在機械零部件可靠性研究的基礎上，提出了一種考慮強度退化過程的機械零部件可靠性靈敏度計算方法，準確的反映了各因素對其可靠度的影響變化規律，結果表明機械零部件的強度退化服從Gamma隨機過程。以履帶車輛底盤傳動系統主動輪為例對考慮強度退化的可靠性靈敏度進行分析，結果表明要提高主動輪可靠度，首先應該增大主動輪的厚度。機械零部件的可靠度受Gamma隨機過程中參數b和c的影響較大，且隨參數b的增大而提高，隨參數c的減小而降低。

[1] 張義民，呂昊. 考慮載荷作用次數的機械零部件可靠性靈敏度分析方法[J]. 工程設計學報，2014, 21(2):119-123.

ZHANG Yimin, Lü Hao. An analytical methodology of reliability and sensitivity analysis for mechanical components considering the times of load action[J]. Chinese Journal of Engineering Design, 2014, 21(2):119-123.

[2] 王正，謝里陽，李兵. 考慮載荷作用次數的零部件可靠性模型[J]. 機械強度，2008, 30(1): 68-71.

WANG Zheng, XIE Liyang, LI Bing. Reliability model of component considering times of random load acting[J]. Journal of Mechanical Strength, 2008, 30(1): 68-71.

[3] 岳玉梅，王正，謝里陽. 考慮載荷作用次數的齒輪可靠度計算模型[J]. 東北大學學報(自然科學版)，2008，29(12)：1754-1756.

YUE Yumei, WANG Zheng, XIE Liyang. Reliability calculation model of a gear considering frequency of random loading actions[J]. Journal of Northeastern University(Natural Science), 2008, 29(12)：1754-1756.

[4] 賀向東，張義民，聞邦椿. 連續梁彎非正態分布參數的壓桿穩定可靠性靈敏度設計[J]. 宇航學報，2007, 28(5):1401-1404.

HE Xiangdong, ZHANG Yimin, WEN Bangchun. Stable reliability sensitivity design of compressive bar with non-normal distribution parameters[J]. Journal of Astronautics, 2007, 28(5):1401-1404.

[5] LEWIS E E. A load-capacity interference model for common-model failures in 1-out-of-2: G system[J]. IEEE Transaction on Reliability, 2001, 50(1):47-51.

[6] LI Jianping, THOMPSON G A. Method to take account of in-homogeneity in mechanical component reliability calculations[J]. IEEE Transactionon Reliability, 2005, 54(1): 159-168.

[7] OVE D. Stochastic model for joint wave and wind loads on offshore structures[J].Structural Safety, 2002, 24: 139-163.

[8] 宋軍，呂震宙. 可靠性靈敏度分析的一種新方法[J]. 航空學報，2010, 29(1): 193-195.

SONG Jun, Lü Zhenzhou. A new reliability sensitivity analysis method[J]. Acta Aeronautica et Astronautica Sinica, 2010, 29(1): 193-195.

[9] NOORTWIJK V J M．A survey of the application of Gamma processes in maintenance[J]．Reliability Engineering and System Safety, 2009, 94(1): 2-21.

[10] 呂春梅，張義民，劉宇，等. 連續梁彎曲振動系統可靠性頻率靈敏度研究[J]. 振動與沖擊，2013, 32(18):159-162.

Lü Chunmei, ZHANG Yimin, LIU Yu, et al. Sensitivity analysis for frequency reliability of a random bending vibration system of continuous beam[J]. Journal of Vibration and Shock, 2013, 32(18): 159-162.

[11] 黃益民，劉偉，劉永壽，等. 充液管道模態的參數靈敏度及其共振可靠性分析[J]. 振動與沖擊，2010, 29(1): 193-195.

HUANG Yimin, LIU Wei, LIU Yongshou, et al. Parameter sensitivity and resonance reliability of a fluid-filled pipeline[J]. Journal of Vibration and Shock, 2010, 29(1): 193-195.

[12] 李云貴，趙國藩．結構可靠度的四階矩分析法[J]．大連理工大學學報, 2012, 32(4): 455-459.

LI Yungui, ZHAO Guofan. Fourth-moment technique on structure reliability[J]. Journal of Dalian University of Technology, 2012, 32(4): 455-459.