淺談對稱性在曲線積分計算中的應用

(濟源職業技術學院 河南 濟源 459000）

曲線積分是微積分計算的一個重要分支，一般的曲線積分繁瑣，麻煩，但當我們注意到問題的對稱性，在積分計算中靈活運用，可大大簡化計算，獲得事半功效的成效.所以，很有必要探究對稱性在積分計算中的應用，特別是在曲線積分、曲面積分中的應用。接下來本文將從兩類曲線積分入手，綜合闡述對稱性在曲線積分計算中的應用。

1.對弧長的曲線積分

設有一弧形型構件占xOy面上的一段曲線L，設構件的質量分布函數為ρ(x,y)，設ρ(x,y)定義在L上且在L上連續，求構件的質量。則有

定義1設L為xOy平面上的一條光滑的簡單曲線弧，f(x,y)在L上有界，在L上任意插入一點列M1，M2，…，Mn-1把L分成n個小弧段 ΔLi=Mi-1Mi的長度為 ΔSi，又(ξi,ηi)是 ΔLi上的任一點，作乘積f(ξi,ηi)ΔSi，記 λ=max{ΔSi}，ΔSi存在，且極限值與 L 的分法及(ξi,ηi)在 ΔLi的取法無關，那么稱極限值為f(x,y)在L上對弧長的曲線積分，記為：

其中f(x,y)叫做被積函數，L叫做積分曲線。

注：

（2）將上述定義推廣，可得空間曲線L上的第一型曲線積分：

對弧長曲線積分的存在性：設f(x,y)在光滑曲線L上連續，那么(x,y)ds一定存在。

對弧長曲線積分的性質：

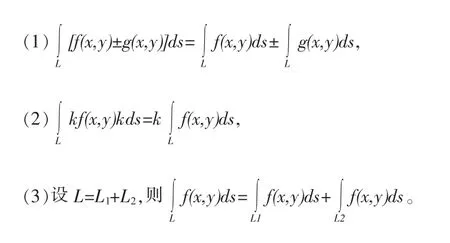
有了上述對弧長的曲線積分的定義，則上面的問題就能夠用對弧長的曲線積分表示為

2.對坐標的曲線積分

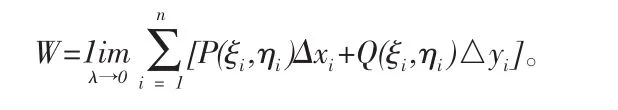
定義2設L=AB是xOy平面上的一條光滑有向曲線弧，P(x,y)、Q(x,y)在 L 上有界，用 L 上的點 M0(x0,y0),M1(x1,y1)，…，Mn(xn,yn)， 把 L分成 n 個小有向弧段 ΔLi=Mi-1Mi，設 Δxi=xi-xi-1,Δyi=yi-yi-1又(ξi,ηi)是ΔLi上的任一點，作乘積 P(ξi,ηi)Δxi，(i=1,2,···,n)，并求和存在，且極限值與 L 的分法及(ξi,ηi)在 ΔLi的取法無關，那么稱極限值為 P(x,y)在 L上對坐標 x的曲線積分，記為：

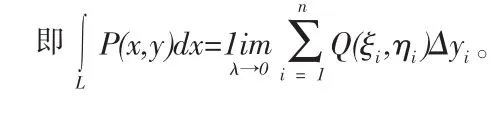
同理定義為 Q(x,y)在 L 上對坐標 y的曲線積分.P(x,y)、Q(x,y)稱為被積函數，L叫做積分曲線。

上述定義可推廣到空間曲線的情形：

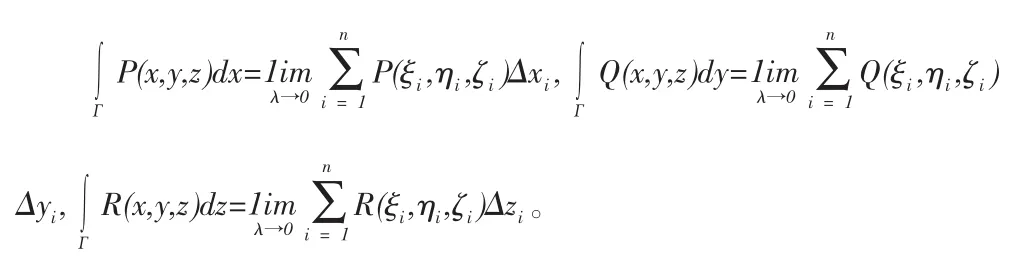
對坐標曲線積分的存在性：設有向曲線L光滑，P(x,y)、Q(x,y)在L上連續，則一定存在。

對坐標曲線積分的性質：

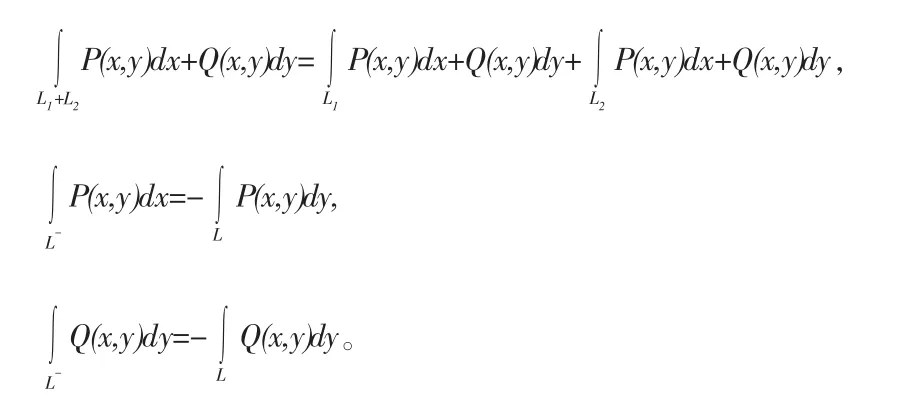
3.第一類曲線積分的對稱問題

定義3設函數f(x,y)定義在二維光滑曲線上，

（1）如果 f(x,y)滿足關系式 f(-x,y)=f(x,y)或 f(x,-y)=f(x,y)，那么稱 f(x,y)為關于x的偶函數或關于y的偶函數。

（2）如果 f(x,y)滿足關系式 f(-x,y)=-f(x,y)或 f(x,-y)=-f(x,y)，那么稱 f(x,y)為關于x的奇函數或關于y的奇函數。

定義4設函數f(x,y,z)定義在三維光滑曲線上。

（1）如果 f(x,y,z)滿足關系式 f(-x,y,z)=f(x,y,z)或 f(x,-y,z)=f(x,y,z)或 f(x,y,-z)=f(x,y,z)，那么稱f(x,y,z)為關于x的或y的或z的偶函數。

（2）如果 f(x,y,z)滿足關系式 f(-x,y,z)=-f(x,y,z)或 f(x,-y,z)=-f(x,y,z)或f(x,y,-z)=-f(x,y,z)，那么稱f(x,y,z)為關于x的或y的或z的奇函數。

定理1設函數f(x,y)定義在二維光滑（或分段光滑）曲線L上，且曲線L關于 ox（或 oy）對稱，則:

定理2設函數f(x,y,z)在三維光滑或（分段光滑）曲線Γ上可積，且曲線Γ對稱于xoy(或yoz或zox)坐標面，則:

（1）當f(x,y,z)為關于z(或x或y)的偶函數時，則有（其中Γ1是Γ位于對稱坐標面一側的部分）。

（2）當f(x,y,z)為關于z(或x或y)奇函數時，則有

推論 設函數f(x,y)定義在二維光滑（或分段光滑）曲線L上，L對稱于ox和oy軸，則:

（2）當f(x,y)是關于x和y中至少某一變量的奇函數時，有

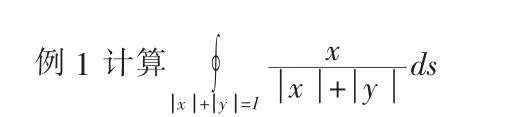
解因為積分曲線既對稱于ox軸又對稱于oy軸，且被積函數f(x,y)=是x的奇函數，故原式

注 此處除運用對稱性之外，還涉及到用積分曲線方程化簡被積函數的技巧。

解 注意到L關于x,y,z的對稱性，則有:

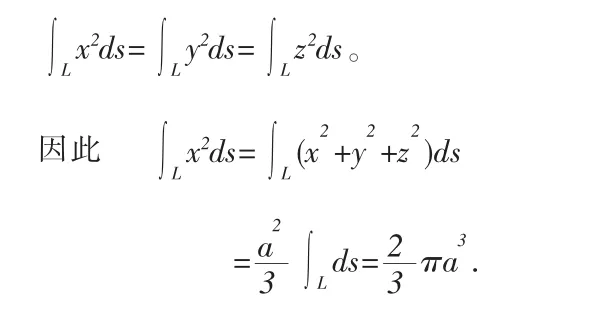
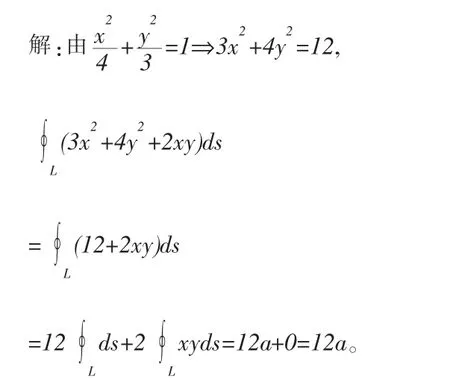
L關于y軸對稱，被積函數xy關于x為奇函數。

4.第二類曲線積分的對稱問題

定理3若L為xoy平面上關于x軸對稱的一條有向光滑曲線弧，其方程是一雙值函數，設為y=±y(x),(a≤x≤b).記 L1,L2分別為L位于x軸的上半部分與下半部分，L1,L2在x軸上的投影的方向相反，函數 P(x,y)，Q(x,y)在 L 上連續，那么:

教材是教師教學和學生學習最重要的載體，某種程度上說，教材呈現的方式和內容決定了教師怎么教和學生如何學，因此通過對不同教材的比較研究，汲取各個教材的長處，對進一步深化課程與教學改革，落實核心素養目標具有重要意義．

解 經分析可知，此處的曲線積分合乎定理3，因而有：

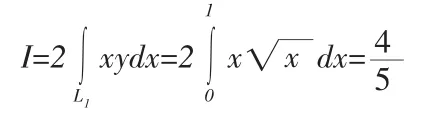
定理4設L為xoy平面上關于y軸對稱的一條有向光滑曲線弧，奇方程為 y=y(x)，（-a≤x≤a），記 L1，L2分別為 L 處于 y 軸的右半部分與左半部分，L1，L2在 x軸上的投影方向相同，函數 P(x,y)，Q(x,y)在L上連續，那么:

定理5設L為xoy平面上關于原點對稱的一條有向光滑曲線弧，奇方程為y=y(x)，（-a≤x≤a），記 L1為L處于 y軸的右半部分與上半部分，L1，L2在x軸上的投影方向相同，函數P(x,y)，Q(x,y)在L上連續，那么:

（1）函數 P(x,y)，Q(x,y)關于(x,y)的偶函數 P(x,y)=P(-x,y),Q(x,y)=Q(-x,-y),則:

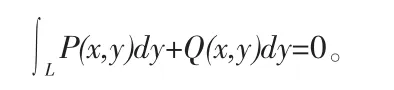
（2）函數 P(x,y)，Q(x,y)關于(x,y)的奇函數 P(x,y)=-P(-x,-y),Q(x,y)=-Q(-x,-y)則：

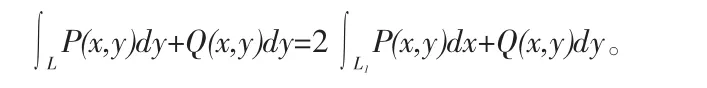
（4）當Q(x,y)關于x為奇函數時，則

定理6設L為xoy平面上具有輪換對稱性的一條有向光滑曲線弧，奇方程為 y=y(x)，(-a≤x≤a)，函數 P(x,y)，Q(x,y)在 L 上連續，那么:

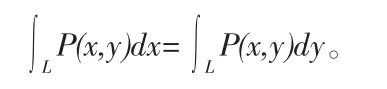
定理7設L為x,y,z上具有輪換對稱性的一條有向光滑曲線弧，函數P(x,y,z)在L上連續，那么:

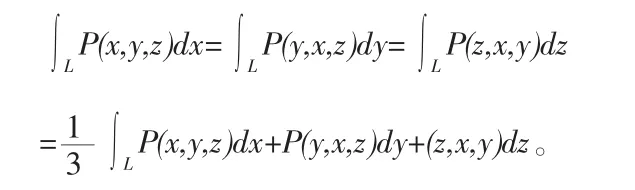
5.結論

通過以上介紹不難看出利用對稱性計算曲線積分與曲面積分不僅是可行的，而且有時還可以起到簡化計算的作用，在學習中可以充分利用對稱性計算曲線積分與曲面積分，提高運算速度和效果，給學習帶來很多方便.使得曲線積分更為簡便、快捷，同時，也有利于避免因符號處理不當而導致的積分錯誤。

【參考文獻】

［1］劉潔，戴長城.對稱性在積分計算中的應用[J].邵陽學院學報：自然科學版，2008：23-27.

［2］劉福貴，魯凱生.利用對稱性計算第二類曲線積分和曲面積分的方法[J].武漢理工大學學報，2006：1069-1072.