談談類比推理
■河南省許昌市建安大道許昌高級中學 胡銀偉
類比是人們從已經掌握了的事物的屬性,推測正在研究中的事物的特性,它以原有認識作基礎,類比出新的結果,由于類比的結果往往是帶有猜測性的,故其結果不一定可靠,但它卻是提出新問題和做出新發現的重要源泉,具有發現的功能。
進行類比推理時,應從具體問題出發,通過觀察、分析、聯想進行對比,提出猜想,找到合適的類比對象是解題的關鍵。類比推理常見有以下三種類型的應用。
類型一 類比定義
由已知熟悉定義類比新定義。
例1 定義“黃金橢圓”:如圖1所示,橢圓中心在坐標原點,F為左焦點,當時,其離心率為,此類橢圓被稱為“黃金橢圓”。類比“黃金橢圓”,試推算出“黃金雙曲線”的離心率e等于( )。


故b2=ac。而b2=c2-a2,所以c2-a2=ac。
在等號兩邊同除以a2得
故答案為A。
方法總結:在求解類比定義型推理試題時,可以借助原定義來求解。
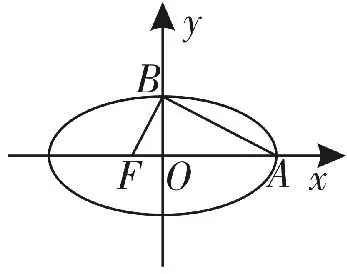
圖1
跟蹤訓練1:定義“等和數列”:在一個數列中,如果每一項與它的后一項的和都為同一個常數,那么這個數列叫作等和數列,這個常數叫作該數列的公和。
已知數列{an}是等和數列,且a1=2,公和為5,那么a18的值為____,這個數列的前n項和Sn的計算公式為____。
解析:由等和數列的定義,知a1+a2=a2+a3=a3+a4=…,即有a1=a3=a5=…,a2=a4=a6=…。又a1=2,公和為5,得a18=a2=5-2=3,即有
類型二 類比性質
性質類比的常見情形有:平面與空間的類比;低維與高維的類比;等差數列與等比數列的類比等。
例2 在平面幾何中有如下結論:正三角形ABC的內切圓面積為S1,外接圓面積為S2,則推廣到空間可以得到類似結論。已知正四面體P-ABC的內切球體積為V1,外接球體積為V2,則等于( )。

解析:如圖2,正三角形的內切圓與外接圓為同心圓,其半徑分別為r1,r2,且r1∶r2=1∶2,所以類比此性質知正四面體P-ABC的內切球與外接球為同心球,其球半徑分別為r、R,則
如圖3所示,正四面體P-ABC中,過點P作PE⊥平面ABC,則E為底面正三角形ABC的中心,球心在PE上,設為O,于是OA=OP=R,OE=r,設正四面體棱長為a,則中有
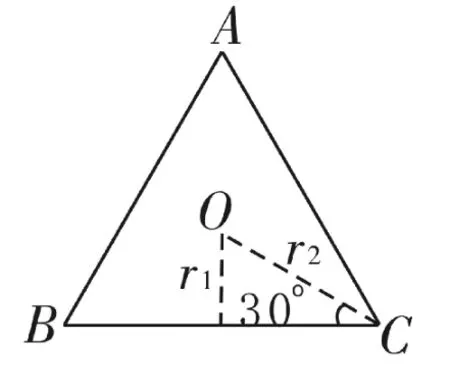
圖2
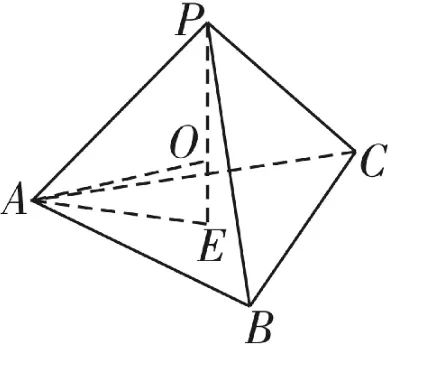
圖3

故答案為D。
方法總結:從一個特殊式子的性質、一個特殊圖形的性質入手,提出類比推理型問題,求解時要認真分析兩者之間的聯系與區別,深入思考兩者的轉化過程是求解的關鍵。
類型三 類比方法
方法類比是由已知熟悉的處理方法類比未知問題的處理方法。常見問題有:數的運算(和與積,乘與乘方,差與除,除與開方)與向量運算類比,圓錐曲線間的類比等。
例3 給出下面類比推理(其中Q為有理數集,R為實數集,C為復數集):
①“若a,b∈R,則a-b=0?a=b”類比推出“a,c∈C,則a-c=0?a=c”;
②“若a,b,c,d∈R,則復數a+bi=c+di?a=c,b=d”類比推出“a,b,c,d∈Q,則
④“若x∈R,則|x|<1?-1<x<1”類比推出“若z∈C,則|z|<1?-1<z<1”。
其中類比結論正確的個數為( )
A.1 B.2 C.3 D.4
解析:類比結論正確的有①②。
故答案為B。
方法總結:有一些處理問題的方法具有類比性,可以把這種方法類比應用到其他問題的求解中。同學們要注意知識的遷移。
跟蹤訓練2:已知△ABC的頂點A、B分別是離心率為e的圓錐曲線的焦點,頂點C在該曲線上。一同學已正確地推得:當m>n>0時有e(sinA+sinB)=sinC。類似地,當m>0,n<0時,有____。

故答案為e|sinA-sinB|=sinC。
此外,我們在進行類比推理時要盡量從本質上去類比,不要被表面現象迷惑,否則只抓住一點表面現象的相似甚至假象去類比,就會犯機械類比的錯誤。

